la_lapack::gesdd Interface Reference

GESDD: computes the singular value decomposition (SVD) of a complex M-by-N matrix A, optionally computing the left and/or right singular vectors, by using divide-and-conquer method. The SVD is written A = U * SIGMA * conjugate-transpose(V) where SIGMA is an M-by-N matrix which is zero except for its min(m,n) diagonal elements, U is an M-by-M unitary matrix, and V is an N-by-N unitary matrix. The diagonal elements of SIGMA are the singular values of A; they are real and non-negative, and are returned in descending order. The first min(m,n) columns of U and V are the left and right singular vectors of A. Note that the routine returns VT = V**H, not V. The divide and conquer algorithm makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none. More...

Public Member Functions
subroutine	cgesdd (jobz, m, n, a, lda, s, u, ldu, vt, ldvt, work, lwork, rwork, iwork, info)
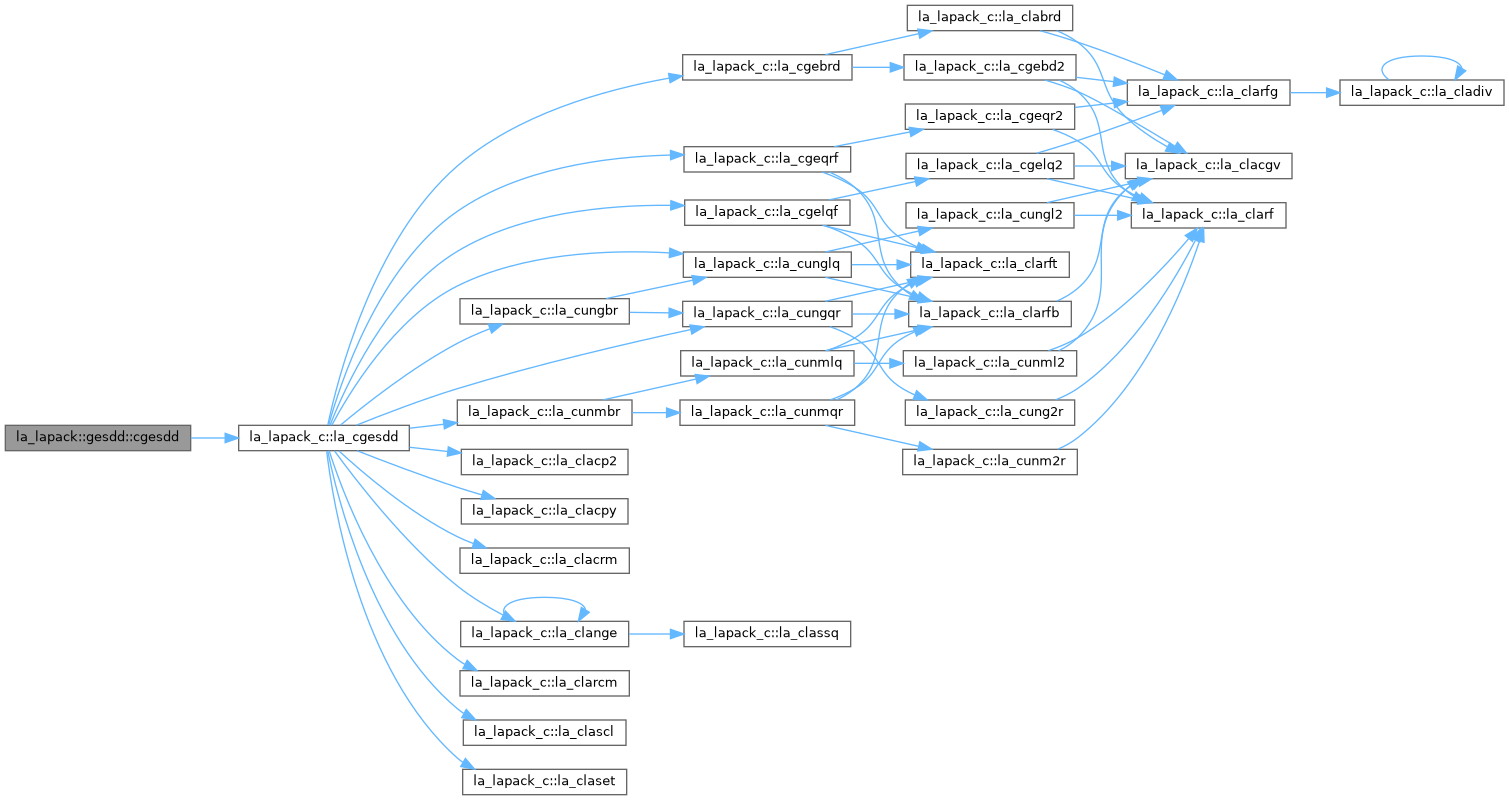
	la_cgesdd
subroutine	dgesdd (jobz, m, n, a, lda, s, u, ldu, vt, ldvt, work, lwork, iwork, info)
	la_dgesdd
	la_qgesdd
subroutine	sgesdd (jobz, m, n, a, lda, s, u, ldu, vt, ldvt, work, lwork, iwork, info)
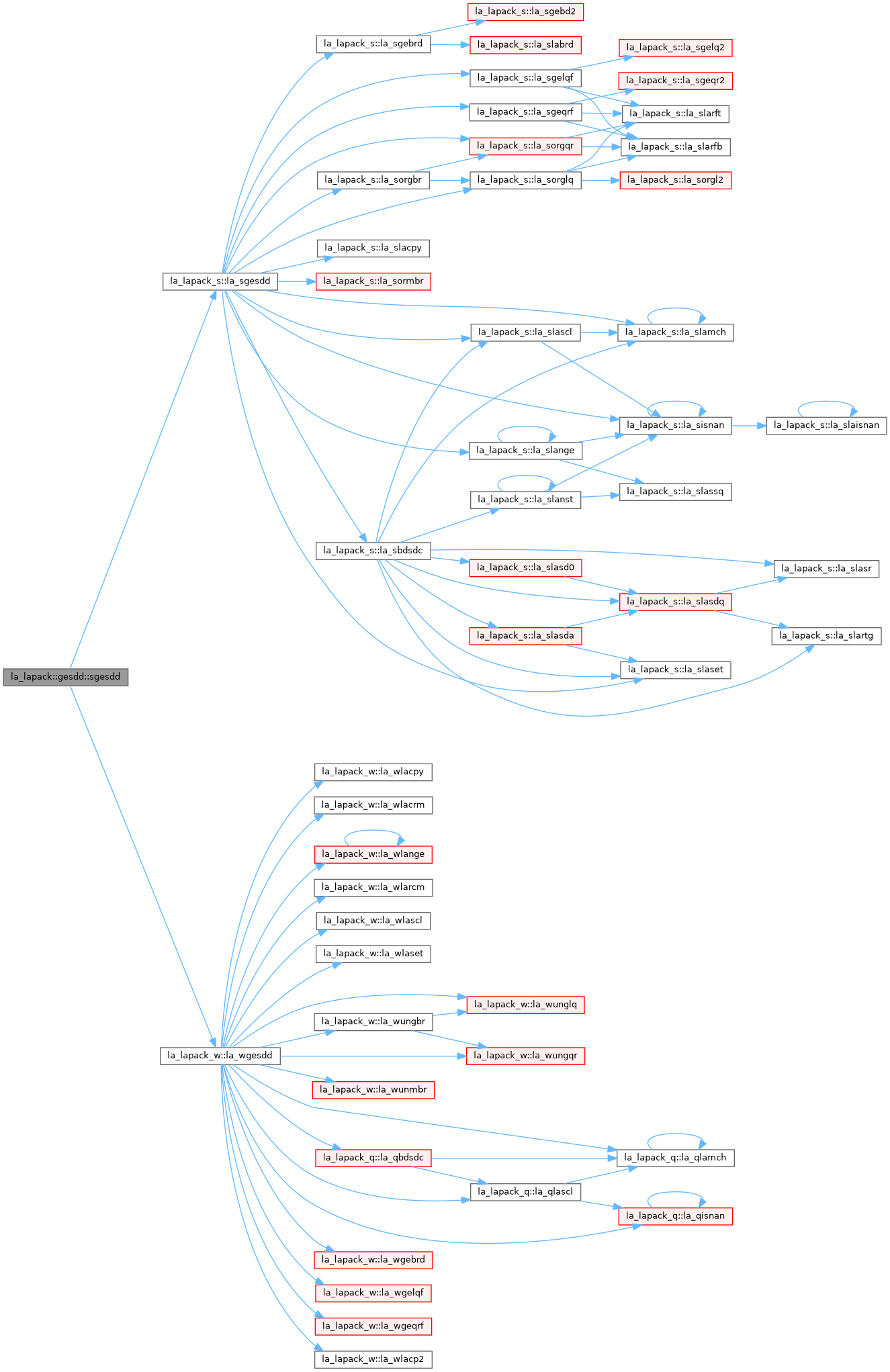
	la_sgesdd
	la_wgesdd
subroutine	zgesdd (jobz, m, n, a, lda, s, u, ldu, vt, ldvt, work, lwork, rwork, iwork, info)
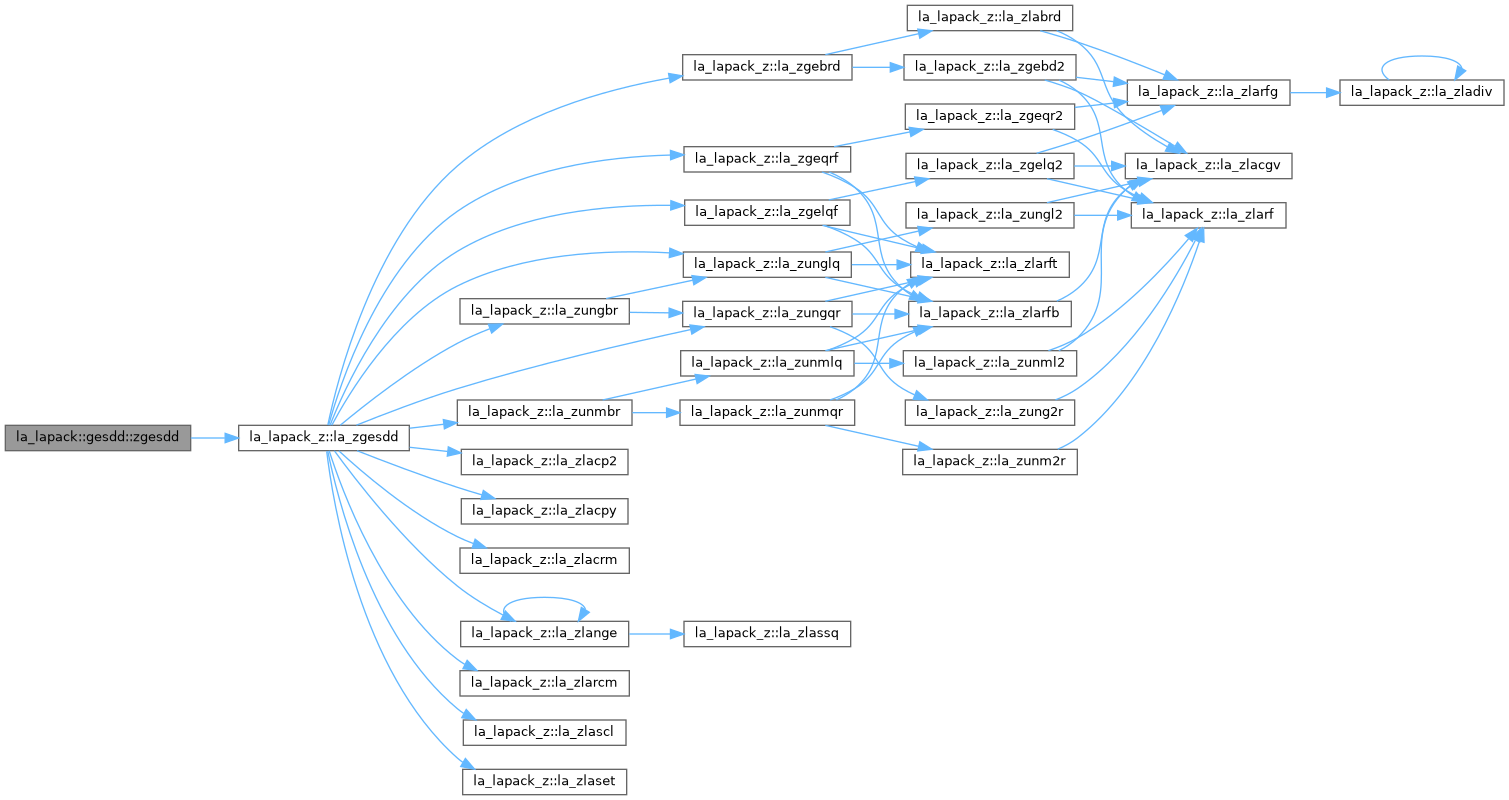
	la_zgesdd

Detailed Description

GESDD: computes the singular value decomposition (SVD) of a complex M-by-N matrix A, optionally computing the left and/or right singular vectors, by using divide-and-conquer method. The SVD is written A = U * SIGMA * conjugate-transpose(V) where SIGMA is an M-by-N matrix which is zero except for its min(m,n) diagonal elements, U is an M-by-M unitary matrix, and V is an N-by-N unitary matrix. The diagonal elements of SIGMA are the singular values of A; they are real and non-negative, and are returned in descending order. The first min(m,n) columns of U and V are the left and right singular vectors of A. Note that the routine returns VT = V**H, not V. The divide and conquer algorithm makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none.

Member Function/Subroutine Documentation

cgesdd()

subroutine la_lapack::gesdd::cgesdd	(	character, intent(in)	jobz,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		complex(sp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(sp), dimension(*), intent(out)	s,
		complex(sp), dimension(ldu,*), intent(out)	u,
		integer(ilp), intent(in)	ldu,
		complex(sp), dimension(ldvt,*), intent(out)	vt,
		integer(ilp), intent(in)	ldvt,
		complex(sp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		real(sp), dimension(*), intent(out)	rwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

Here is the call graph for this function:

dgesdd()

subroutine la_lapack::gesdd::dgesdd	(	character, intent(in)	jobz,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	s,
		real(dp), dimension(ldu,*), intent(out)	u,
		integer(ilp), intent(in)	ldu,
		real(dp), dimension(ldvt,*), intent(out)	vt,
		integer(ilp), intent(in)	ldvt,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

Here is the call graph for this function:

la_cgesdd()

la_lapack::gesdd::la_cgesdd

la_dgesdd()

la_lapack::gesdd::la_dgesdd

la_qgesdd()

la_lapack::gesdd::la_qgesdd

la_sgesdd()

la_lapack::gesdd::la_sgesdd

la_wgesdd()

la_lapack::gesdd::la_wgesdd

la_zgesdd()

la_lapack::gesdd::la_zgesdd

sgesdd()

subroutine la_lapack::gesdd::sgesdd	(	character, intent(in)	jobz,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(sp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(sp), dimension(*), intent(out)	s,
		real(sp), dimension(ldu,*), intent(out)	u,
		integer(ilp), intent(in)	ldu,
		real(sp), dimension(ldvt,*), intent(out)	vt,
		integer(ilp), intent(in)	ldvt,
		real(sp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

Here is the call graph for this function:

zgesdd()

subroutine la_lapack::gesdd::zgesdd	(	character, intent(in)	jobz,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		complex(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	s,
		complex(dp), dimension(ldu,*), intent(out)	u,
		integer(ilp), intent(in)	ldu,
		complex(dp), dimension(ldvt,*), intent(out)	vt,
		integer(ilp), intent(in)	ldvt,
		complex(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		real(dp), dimension(*), intent(out)	rwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

Here is the call graph for this function:

---

The documentation for this interface was generated from the following file:

• la_lapack.f90