la_lapack_d Module Reference

Functions/Subroutines
pure subroutine, public	la_dgbtf2 (m, n, kl, ku, ab, ldab, ipiv, info)
	DGBTF2: computes an LU factorization of a real m-by-n band matrix A using partial pivoting with row interchanges. This is the unblocked version of the algorithm, calling Level 2 BLAS.
pure subroutine, public	la_dgbtrs (trans, n, kl, ku, nrhs, ab, ldab, ipiv, b, ldb, info)
	DGBTRS: solves a system of linear equations A * X = B or A**T * X = B with a general band matrix A using the LU factorization computed by DGBTRF.
pure subroutine, public	la_dgebak (job, side, n, ilo, ihi, scale, m, v, ldv, info)
	DGEBAK: forms the right or left eigenvectors of a real general matrix by backward transformation on the computed eigenvectors of the balanced matrix output by DGEBAL.
pure subroutine, public	la_dggbak (job, side, n, ilo, ihi, lscale, rscale, m, v, ldv, info)
	DGGBAK: forms the right or left eigenvectors of a real generalized eigenvalue problem A*x = lambda*B*x, by backward transformation on the computed eigenvectors of the balanced pair of matrices output by DGGBAL.
pure subroutine, public	la_dgtsv (n, nrhs, dl, d, du, b, ldb, info)
	DGTSV: solves the equation A*X = B, where A is an n by n tridiagonal matrix, by Gaussian elimination with partial pivoting. Note that the equation A**T*X = B may be solved by interchanging the order of the arguments DU and DL.
pure subroutine, public	la_dgttrf (n, dl, d, du, du2, ipiv, info)
	DGTTRF: computes an LU factorization of a real tridiagonal matrix A using elimination with partial pivoting and row interchanges. The factorization has the form A = L * U where L is a product of permutation and unit lower bidiagonal matrices and U is upper triangular with nonzeros in only the main diagonal and first two superdiagonals.
pure subroutine, public	la_dgtts2 (itrans, n, nrhs, dl, d, du, du2, ipiv, b, ldb)
	DGTTS2: solves one of the systems of equations A*X = B or A**T*X = B, with a tridiagonal matrix A using the LU factorization computed by DGTTRF.
pure real(dp) function, public	la_dla_gbrpvgrw (n, kl, ku, ncols, ab, ldab, afb, ldafb)
	DLA_GBRPVGRW: computes the reciprocal pivot growth factor norm(A)/norm(U). The "max absolute element" norm is used. If this is much less than 1, the stability of the LU factorization of the (equilibrated) matrix A could be poor. This also means that the solution X, estimated condition numbers, and error bounds could be unreliable.
pure real(dp) function, public	la_dla_gerpvgrw (n, ncols, a, lda, af, ldaf)
	DLA_GERPVGRW: computes the reciprocal pivot growth factor norm(A)/norm(U). The "max absolute element" norm is used. If this is much less than 1, the stability of the LU factorization of the (equilibrated) matrix A could be poor. This also means that the solution X, estimated condition numbers, and error bounds could be unreliable.
pure subroutine, public	la_dla_wwaddw (n, x, y, w)
	DLA_WWADDW: adds a vector W into a doubled-single vector (X, Y). This works for all extant IBM's hex and binary floating point arithmetic, but not for decimal.
pure subroutine, public	la_dlabad (small, large)
	DLABAD: takes as input the values computed by DLAMCH for underflow and overflow, and returns the square root of each of these values if the log of LARGE is sufficiently large. This subroutine is intended to identify machines with a large exponent range, such as the Crays, and redefine the underflow and overflow limits to be the square roots of the values computed by DLAMCH. This subroutine is needed because DLAMCH does not compensate for poor arithmetic in the upper half of the exponent range, as is found on a Cray.
pure subroutine, public	la_dlacn2 (n, v, x, isgn, est, kase, isave)
	DLACN2: estimates the 1-norm of a square, real matrix A. Reverse communication is used for evaluating matrix-vector products.
subroutine, public	la_dlacon (n, v, x, isgn, est, kase)
	DLACON: estimates the 1-norm of a square, real matrix A. Reverse communication is used for evaluating matrix-vector products.
pure subroutine, public	la_dlacpy (uplo, m, n, a, lda, b, ldb)
	DLACPY: copies all or part of a two-dimensional matrix A to another matrix B.
pure real(dp) function, public	la_dladiv2 (a, b, c, d, r, t)
pure subroutine, public	la_dlae2 (a, b, c, rt1, rt2)
	DLAE2: computes the eigenvalues of a 2-by-2 symmetric matrix [ A B ] [ B C ]. On return, RT1 is the eigenvalue of larger absolute value, and RT2 is the eigenvalue of smaller absolute value.
pure subroutine, public	la_dlaebz (ijob, nitmax, n, mmax, minp, nbmin, abstol, reltol, pivmin, d, e, e2, nval, ab, c, mout, nab, work, iwork, info)
	DLAEBZ: contains the iteration loops which compute and use the function N(w), which is the count of eigenvalues of a symmetric tridiagonal matrix T less than or equal to its argument w. It performs a choice of two types of loops: IJOB=1, followed by IJOB=2: It takes as input a list of intervals and returns a list of sufficiently small intervals whose union contains the same eigenvalues as the union of the original intervals. The input intervals are (AB(j,1),AB(j,2)], j=1,...,MINP. The output interval (AB(j,1),AB(j,2)] will contain eigenvalues NAB(j,1)+1,...,NAB(j,2), where 1 <= j <= MOUT. IJOB=3: It performs a binary search in each input interval (AB(j,1),AB(j,2)] for a point w(j) such that N(w(j))=NVAL(j), and uses C(j) as the starting point of the search. If such a w(j) is found, then on output AB(j,1)=AB(j,2)=w. If no such w(j) is found, then on output (AB(j,1),AB(j,2)] will be a small interval containing the point where N(w) jumps through NVAL(j), unless that point lies outside the initial interval. Note that the intervals are in all cases half-open intervals, i.e., of the form (a,b] , which includes b but not a . To avoid underflow, the matrix should be scaled so that its largest element is no greater than overflow**(1/2) * underflow**(1/4) in absolute value. To assure the most accurate computation of small eigenvalues, the matrix should be scaled to be not much smaller than that, either. See W. Kahan "Accurate Eigenvalues of a Symmetric Tridiagonal Matrix", Report CS41, Computer Science Dept., Stanford University, July 21, 1966 Note: the arguments are, in general, not checked for unreasonable values.
pure subroutine, public	la_dlaed5 (i, d, z, delta, rho, dlam)
	This subroutine computes the I-th eigenvalue of a symmetric rank-one modification of a 2-by-2 diagonal matrix diag( D ) + RHO * Z * transpose(Z) . The diagonal elements in the array D are assumed to satisfy D(i) < D(j) for i < j . We also assume RHO > 0 and that the Euclidean norm of the vector Z is one.
pure subroutine, public	la_dlaeda (n, tlvls, curlvl, curpbm, prmptr, perm, givptr, givcol, givnum, q, qptr, z, ztemp, info)
	DLAEDA: computes the Z vector corresponding to the merge step in the CURLVLth step of the merge process with TLVLS steps for the CURPBMth problem.
pure subroutine, public	la_dlaev2 (a, b, c, rt1, rt2, cs1, sn1)
	DLAEV2: computes the eigendecomposition of a 2-by-2 symmetric matrix [ A B ] [ B C ]. On return, RT1 is the eigenvalue of larger absolute value, RT2 is the eigenvalue of smaller absolute value, and (CS1,SN1) is the unit right eigenvector for RT1, giving the decomposition [ CS1 SN1 ] [ A B ] [ CS1 -SN1 ] = [ RT1 0 ] [-SN1 CS1 ] [ B C ] [ SN1 CS1 ] [ 0 RT2 ].
pure subroutine, public	la_dlag2 (a, lda, b, ldb, safmin, scale1, scale2, wr1, wr2, wi)
	DLAG2: computes the eigenvalues of a 2 x 2 generalized eigenvalue problem A - w B, with scaling as necessary to avoid over-/underflow. The scaling factor "s" results in a modified eigenvalue equation s A - w B where s is a non-negative scaling factor chosen so that w, w B, and s A do not overflow and, if possible, do not underflow, either.
pure subroutine, public	la_dlag2s (m, n, a, lda, sa, ldsa, info)
	DLAG2S: converts a DOUBLE PRECISION matrix, SA, to a SINGLE PRECISION matrix, A. RMAX is the overflow for the SINGLE PRECISION arithmetic DLAG2S checks that all the entries of A are between -RMAX and RMAX. If not the conversion is aborted and a flag is raised. This is an auxiliary routine so there is no argument checking.
pure subroutine, public	la_dlagtm (trans, n, nrhs, alpha, dl, d, du, x, ldx, beta, b, ldb)
	DLAGTM: performs a matrix-vector product of the form B := alpha * A * X + beta * B where A is a tridiagonal matrix of order N, B and X are N by NRHS matrices, and alpha and beta are real scalars, each of which may be 0., 1., or -1.
pure logical(lk) function, public	la_dlaisnan (din1, din2)
	This routine is not for general use. It exists solely to avoid over-optimization in DISNAN. DLAISNAN: checks for NaNs by comparing its two arguments for inequality. NaN is the only floating-point value where NaN != NaN returns .TRUE. To check for NaNs, pass the same variable as both arguments. A compiler must assume that the two arguments are not the same variable, and the test will not be optimized away. Interprocedural or whole-program optimization may delete this test. The ISNAN functions will be replaced by the correct Fortran 03 intrinsic once the intrinsic is widely available.
pure real(dp) function, public	la_dlamch (cmach)
	DLAMCH: determines double precision machine parameters.
pure real(dp) function, public	la_dlamc3 (a, b)
pure subroutine, public	la_dlamrg (n1, n2, a, dtrd1, dtrd2, index)
	DLAMRG: will create a permutation list which will merge the elements of A (which is composed of two independently sorted sets) into a single set which is sorted in ascending order.
pure recursive subroutine, public	la_dlaorhr_col_getrfnp2 (m, n, a, lda, d, info)
	DLAORHR_COL_GETRFNP2: computes the modified LU factorization without pivoting of a real general M-by-N matrix A. The factorization has the form: A - S = L * U, where: S is a m-by-n diagonal sign matrix with the diagonal D, so that D(i) = S(i,i), 1 <= i <= min(M,N). The diagonal D is constructed as D(i)=-SIGN(A(i,i)), where A(i,i) is the value after performing i-1 steps of Gaussian elimination. This means that the diagonal element at each step of "modified" Gaussian elimination is at least one in absolute value (so that division-by-zero not possible during the division by the diagonal element); L is a M-by-N lower triangular matrix with unit diagonal elements (lower trapezoidal if M > N); and U is a M-by-N upper triangular matrix (upper trapezoidal if M < N). This routine is an auxiliary routine used in the Householder reconstruction routine DORHR_COL. In DORHR_COL, this routine is applied to an M-by-N matrix A with orthonormal columns, where each element is bounded by one in absolute value. With the choice of the matrix S above, one can show that the diagonal element at each step of Gaussian elimination is the largest (in absolute value) in the column on or below the diagonal, so that no pivoting is required for numerical stability [1]. For more details on the Householder reconstruction algorithm, including the modified LU factorization, see [1]. This is the recursive version of the LU factorization algorithm. Denote A - S by B. The algorithm divides the matrix B into four submatrices: [ B11 | B12 ] where B11 is n1 by n1, B = [ --—|--— ] B21 is (m-n1) by n1, [ B21 | B22 ] B12 is n1 by n2, B22 is (m-n1) by n2, with n1 = min(m,n)/2, n2 = n-n1. The subroutine calls itself to factor B11, solves for B21, solves for B12, updates B22, then calls itself to factor B22. For more details on the recursive LU algorithm, see [2]. DLAORHR_COL_GETRFNP2 is called to factorize a block by the blocked routine DLAORHR_COL_GETRFNP, which uses blocked code calling Level 3 BLAS to update the submatrix. However, DLAORHR_COL_GETRFNP2 is self-sufficient and can be used without DLAORHR_COL_GETRFNP. [1] "Reconstructing Householder vectors from tall-skinny QR", G. Ballard, J. Demmel, L. Grigori, M. Jacquelin, H.D. Nguyen, E. Solomonik, J. Parallel Distrib. Comput., vol. 85, pp. 3-31, 2015. [2] "Recursion leads to automatic variable blocking for dense linear algebra algorithms", F. Gustavson, IBM J. of Res. and Dev., vol. 41, no. 6, pp. 737-755, 1997.
pure subroutine, public	la_dlapmr (forwrd, m, n, x, ldx, k)
	DLAPMR: rearranges the rows of the M by N matrix X as specified by the permutation K(1),K(2),...,K(M) of the integers 1,...,M. If FORWRD = .TRUE., forward permutation: X(K(I),*) is moved X(I,*) for I = 1,2,...,M. If FORWRD = .FALSE., backward permutation: X(I,*) is moved to X(K(I),*) for I = 1,2,...,M.
pure subroutine, public	la_dlapmt (forwrd, m, n, x, ldx, k)
	DLAPMT: rearranges the columns of the M by N matrix X as specified by the permutation K(1),K(2),...,K(N) of the integers 1,...,N. If FORWRD = .TRUE., forward permutation: X(*,K(J)) is moved X(*,J) for J = 1,2,...,N. If FORWRD = .FALSE., backward permutation: X(*,J) is moved to X(*,K(J)) for J = 1,2,...,N.
pure real(dp) function, public	la_dlapy3 (x, y, z)
	DLAPY3: returns sqrt(x**2+y**2+z**2), taking care not to cause unnecessary overflow and unnecessary underflow.
pure subroutine, public	la_dlaqgb (m, n, kl, ku, ab, ldab, r, c, rowcnd, colcnd, amax, equed)
	DLAQGB: equilibrates a general M by N band matrix A with KL subdiagonals and KU superdiagonals using the row and scaling factors in the vectors R and C.
pure subroutine, public	la_dlaqge (m, n, a, lda, r, c, rowcnd, colcnd, amax, equed)
	DLAQGE: equilibrates a general M by N matrix A using the row and column scaling factors in the vectors R and C.
pure subroutine, public	la_dlaqr1 (n, h, ldh, sr1, si1, sr2, si2, v)
	Given a 2-by-2 or 3-by-3 matrix H, DLAQR1: sets v to a scalar multiple of the first column of the product (*) K = (H - (sr1 + i*si1)*I)*(H - (sr2 + i*si2)*I) scaling to avoid overflows and most underflows. It is assumed that either 1) sr1 = sr2 and si1 = -si2 or 2) si1 = si2 = 0. This is useful for starting double implicit shift bulges in the QR algorithm.
pure subroutine, public	la_dlaqsb (uplo, n, kd, ab, ldab, s, scond, amax, equed)
	DLAQSB: equilibrates a symmetric band matrix A using the scaling factors in the vector S.
pure subroutine, public	la_dlaqsp (uplo, n, ap, s, scond, amax, equed)
	DLAQSP: equilibrates a symmetric matrix A using the scaling factors in the vector S.
pure subroutine, public	la_dlaqsy (uplo, n, a, lda, s, scond, amax, equed)
	DLAQSY: equilibrates a symmetric matrix A using the scaling factors in the vector S.
pure subroutine, public	la_dlar2v (n, x, y, z, incx, c, s, incc)
	DLAR2V: applies a vector of real plane rotations from both sides to a sequence of 2-by-2 real symmetric matrices, defined by the elements of the vectors x, y and z. For i = 1,2,...,n ( x(i) z(i) ) := ( c(i) s(i) ) ( x(i) z(i) ) ( c(i) -s(i) ) ( z(i) y(i) ) ( -s(i) c(i) ) ( z(i) y(i) ) ( s(i) c(i) )
pure subroutine, public	la_dlarf (side, m, n, v, incv, tau, c, ldc, work)
	DLARF: applies a real elementary reflector H to a real m by n matrix C, from either the left or the right. H is represented in the form H = I - tau * v * v**T where tau is a real scalar and v is a real vector. If tau = 0, then H is taken to be the unit matrix.
pure subroutine, public	la_dlarfb (side, trans, direct, storev, m, n, k, v, ldv, t, ldt, c, ldc, work, ldwork)
	DLARFB: applies a real block reflector H or its transpose H**T to a real m by n matrix C, from either the left or the right.
pure subroutine, public	la_dlarfb_gett (ident, m, n, k, t, ldt, a, lda, b, ldb, work, ldwork)
	DLARFB_GETT: applies a real Householder block reflector H from the left to a real (K+M)-by-N "triangular-pentagonal" matrix composed of two block matrices: an upper trapezoidal K-by-N matrix A stored in the array A, and a rectangular M-by-(N-K) matrix B, stored in the array B. The block reflector H is stored in a compact WY-representation, where the elementary reflectors are in the arrays A, B and T. See Further Details section.
pure subroutine, public	la_dlarft (direct, storev, n, k, v, ldv, tau, t, ldt)
	DLARFT: forms the triangular factor T of a real block reflector H of order n, which is defined as a product of k elementary reflectors. If DIRECT = 'F', H = H(1) H(2) . . . H(k) and T is upper triangular; If DIRECT = 'B', H = H(k) . . . H(2) H(1) and T is lower triangular. If STOREV = 'C', the vector which defines the elementary reflector H(i) is stored in the i-th column of the array V, and H = I - V * T * V**T If STOREV = 'R', the vector which defines the elementary reflector H(i) is stored in the i-th row of the array V, and H = I - V**T * T * V.
pure subroutine, public	la_dlarfx (side, m, n, v, tau, c, ldc, work)
	DLARFX: applies a real elementary reflector H to a real m by n matrix C, from either the left or the right. H is represented in the form H = I - tau * v * v**T where tau is a real scalar and v is a real vector. If tau = 0, then H is taken to be the unit matrix This version uses inline code if H has order < 11.
pure subroutine, public	la_dlarfy (uplo, n, v, incv, tau, c, ldc, work)
	DLARFY: applies an elementary reflector, or Householder matrix, H, to an n x n symmetric matrix C, from both the left and the right. H is represented in the form H = I - tau * v * v' where tau is a scalar and v is a vector. If tau is zero, then H is taken to be the unit matrix.
pure subroutine, public	la_dlargv (n, x, incx, y, incy, c, incc)
	DLARGV: generates a vector of real plane rotations, determined by elements of the real vectors x and y. For i = 1,2,...,n ( c(i) s(i) ) ( x(i) ) = ( a(i) ) ( -s(i) c(i) ) ( y(i) ) = ( 0 )
pure subroutine, public	la_dlarra (n, d, e, e2, spltol, tnrm, nsplit, isplit, info)
	Compute the splitting points with threshold SPLTOL. DLARRA: sets any "small" off-diagonal elements to zero.
pure subroutine, public	la_dlarrc (jobt, n, vl, vu, d, e, pivmin, eigcnt, lcnt, rcnt, info)
	Find the number of eigenvalues of the symmetric tridiagonal matrix T that are in the interval (VL,VU] if JOBT = 'T', and of L D L^T if JOBT = 'L'.
pure subroutine, public	la_dlarrd (range, order, n, vl, vu, il, iu, gers, reltol, d, e, e2, pivmin, nsplit, isplit, m, w, werr, wl, wu, iblock, indexw, work, iwork, info)
	DLARRD: computes the eigenvalues of a symmetric tridiagonal matrix T to suitable accuracy. This is an auxiliary code to be called from DSTEMR. The user may ask for all eigenvalues, all eigenvalues in the half-open interval (VL, VU], or the IL-th through IU-th eigenvalues. To avoid overflow, the matrix must be scaled so that its largest element is no greater than overflow**(1/2) * underflow**(1/4) in absolute value, and for greatest accuracy, it should not be much smaller than that. See W. Kahan "Accurate Eigenvalues of a Symmetric Tridiagonal Matrix", Report CS41, Computer Science Dept., Stanford University, July 21, 1966.
pure subroutine, public	la_dlarrj (n, d, e2, ifirst, ilast, rtol, offset, w, werr, work, iwork, pivmin, spdiam, info)
	Given the initial eigenvalue approximations of T, DLARRJ: does bisection to refine the eigenvalues of T, W( IFIRST-OFFSET ) through W( ILAST-OFFSET ), to more accuracy. Initial guesses for these eigenvalues are input in W, the corresponding estimate of the error in these guesses in WERR. During bisection, intervals [left, right] are maintained by storing their mid-points and semi-widths in the arrays W and WERR respectively.
pure subroutine, public	la_dlarrk (n, iw, gl, gu, d, e2, pivmin, reltol, w, werr, info)
	DLARRK: computes one eigenvalue of a symmetric tridiagonal matrix T to suitable accuracy. This is an auxiliary code to be called from DSTEMR. To avoid overflow, the matrix must be scaled so that its largest element is no greater than overflow**(1/2) * underflow**(1/4) in absolute value, and for greatest accuracy, it should not be much smaller than that. See W. Kahan "Accurate Eigenvalues of a Symmetric Tridiagonal Matrix", Report CS41, Computer Science Dept., Stanford University, July 21, 1966.
pure subroutine, public	la_dlarrr (n, d, e, info)
	Perform tests to decide whether the symmetric tridiagonal matrix T warrants expensive computations which guarantee high relative accuracy in the eigenvalues.
pure subroutine, public	la_dlartg (f, g, c, s, r)
	!
pure subroutine, public	la_dlartgp (f, g, cs, sn, r)
	DLARTGP: generates a plane rotation so that [ CS SN ] . [ F ] = [ R ] where CS**2 + SN**2 = 1. [ -SN CS ] [ G ] [ 0 ] This is a slower, more accurate version of the Level 1 BLAS routine DROTG, with the following other differences: F and G are unchanged on return. If G=0, then CS=(+/-)1 and SN=0. If F=0 and (G .ne. 0), then CS=0 and SN=(+/-)1. The sign is chosen so that R >= 0.
pure subroutine, public	la_dlartgs (x, y, sigma, cs, sn)
	DLARTGS: generates a plane rotation designed to introduce a bulge in Golub-Reinsch-style implicit QR iteration for the bidiagonal SVD problem. X and Y are the top-row entries, and SIGMA is the shift. The computed CS and SN define a plane rotation satisfying [ CS SN ] . [ X^2 - SIGMA ] = [ R ], [ -SN CS ] [ X * Y ] [ 0 ] with R nonnegative. If X^2 - SIGMA and X * Y are 0, then the rotation is by PI/2.
pure subroutine, public	la_dlartv (n, x, incx, y, incy, c, s, incc)
	DLARTV: applies a vector of real plane rotations to elements of the real vectors x and y. For i = 1,2,...,n ( x(i) ) := ( c(i) s(i) ) ( x(i) ) ( y(i) ) ( -s(i) c(i) ) ( y(i) )
pure subroutine, public	la_dlaruv (iseed, n, x)
	DLARUV: returns a vector of n random real numbers from a uniform (0,1) distribution (n <= 128). This is an auxiliary routine called by DLARNV and ZLARNV.
pure subroutine, public	la_dlarz (side, m, n, l, v, incv, tau, c, ldc, work)
	DLARZ: applies a real elementary reflector H to a real M-by-N matrix C, from either the left or the right. H is represented in the form H = I - tau * v * v**T where tau is a real scalar and v is a real vector. If tau = 0, then H is taken to be the unit matrix. H is a product of k elementary reflectors as returned by DTZRZF.
pure subroutine, public	la_dlarzb (side, trans, direct, storev, m, n, k, l, v, ldv, t, ldt, c, ldc, work, ldwork)
	DLARZB: applies a real block reflector H or its transpose H**T to a real distributed M-by-N C from the left or the right. Currently, only STOREV = 'R' and DIRECT = 'B' are supported.
pure subroutine, public	la_dlarzt (direct, storev, n, k, v, ldv, tau, t, ldt)
	DLARZT: forms the triangular factor T of a real block reflector H of order > n, which is defined as a product of k elementary reflectors. If DIRECT = 'F', H = H(1) H(2) . . . H(k) and T is upper triangular; If DIRECT = 'B', H = H(k) . . . H(2) H(1) and T is lower triangular. If STOREV = 'C', the vector which defines the elementary reflector H(i) is stored in the i-th column of the array V, and H = I - V * T * V**T If STOREV = 'R', the vector which defines the elementary reflector H(i) is stored in the i-th row of the array V, and H = I - V**T * T * V Currently, only STOREV = 'R' and DIRECT = 'B' are supported.
pure subroutine, public	la_dlas2 (f, g, h, ssmin, ssmax)
	DLAS2: computes the singular values of the 2-by-2 matrix [ F G ] [ 0 H ]. On return, SSMIN is the smaller singular value and SSMAX is the larger singular value.
pure subroutine, public	la_dlasd5 (i, d, z, delta, rho, dsigma, work)
	This subroutine computes the square root of the I-th eigenvalue of a positive symmetric rank-one modification of a 2-by-2 diagonal matrix diag( D ) * diag( D ) + RHO * Z * transpose(Z) . The diagonal entries in the array D are assumed to satisfy 0 <= D(i) < D(j) for i < j . We also assume RHO > 0 and that the Euclidean norm of the vector Z is one.
pure subroutine, public	la_dlasdt (n, lvl, nd, inode, ndiml, ndimr, msub)
	DLASDT: creates a tree of subproblems for bidiagonal divide and conquer.
pure subroutine, public	la_dlaset (uplo, m, n, alpha, beta, a, lda)
	DLASET: initializes an m-by-n matrix A to BETA on the diagonal and ALPHA on the offdiagonals.
pure subroutine, public	la_dlasq4 (i0, n0, z, pp, n0in, dmin, dmin1, dmin2, dn, dn1, dn2, tau, ttype, g)
	DLASQ4: computes an approximation TAU to the smallest eigenvalue using values of d from the previous transform.
pure subroutine, public	la_dlasq5 (i0, n0, z, pp, tau, sigma, dmin, dmin1, dmin2, dn, dnm1, dnm2, ieee, eps)
	DLASQ5: computes one dqds transform in ping-pong form, one version for IEEE machines another for non IEEE machines.
pure subroutine, public	la_dlasq6 (i0, n0, z, pp, dmin, dmin1, dmin2, dn, dnm1, dnm2)
	DLASQ6: computes one dqd (shift equal to zero) transform in ping-pong form, with protection against underflow and overflow.
pure subroutine, public	la_dlasr (side, pivot, direct, m, n, c, s, a, lda)
	DLASR: applies a sequence of plane rotations to a real matrix A, from either the left or the right. When SIDE = 'L', the transformation takes the form A := P*A and when SIDE = 'R', the transformation takes the form A := A*P**T where P is an orthogonal matrix consisting of a sequence of z plane rotations, with z = M when SIDE = 'L' and z = N when SIDE = 'R', and P**T is the transpose of P. When DIRECT = 'F' (Forward sequence), then P = P(z-1) * ... * P(2) * P(1) and when DIRECT = 'B' (Backward sequence), then P = P(1) * P(2) * ... * P(z-1) where P(k) is a plane rotation matrix defined by the 2-by-2 rotation R(k) = ( c(k) s(k) ) = ( -s(k) c(k) ). When PIVOT = 'V' (Variable pivot), the rotation is performed for the plane (k,k+1), i.e., P(k) has the form P(k) = ( 1 ) ( ... ) ( 1 ) ( c(k) s(k) ) ( -s(k) c(k) ) ( 1 ) ( ... ) ( 1 ) where R(k) appears as a rank-2 modification to the identity matrix in rows and columns k and k+1. When PIVOT = 'T' (Top pivot), the rotation is performed for the plane (1,k+1), so P(k) has the form P(k) = ( c(k) s(k) ) ( 1 ) ( ... ) ( 1 ) ( -s(k) c(k) ) ( 1 ) ( ... ) ( 1 ) where R(k) appears in rows and columns 1 and k+1. Similarly, when PIVOT = 'B' (Bottom pivot), the rotation is performed for the plane (k,z), giving P(k) the form P(k) = ( 1 ) ( ... ) ( 1 ) ( c(k) s(k) ) ( 1 ) ( ... ) ( 1 ) ( -s(k) c(k) ) where R(k) appears in rows and columns k and z. The rotations are performed without ever forming P(k) explicitly.
pure subroutine, public	la_dlasrt (id, n, d, info)
	Sort the numbers in D in increasing order (if ID = 'I') or in decreasing order (if ID = 'D' ). Use Quick Sort, reverting to Insertion sort on arrays of size <= 20. Dimension of STACK limits N to about 2**32.
pure subroutine, public	la_dlassq (n, x, incx, scl, sumsq)
	!
pure subroutine, public	la_dlasv2 (f, g, h, ssmin, ssmax, snr, csr, snl, csl)
	DLASV2: computes the singular value decomposition of a 2-by-2 triangular matrix [ F G ] [ 0 H ]. On return, abs(SSMAX) is the larger singular value, abs(SSMIN) is the smaller singular value, and (CSL,SNL) and (CSR,SNR) are the left and right singular vectors for abs(SSMAX), giving the decomposition [ CSL SNL ] [ F G ] [ CSR -SNR ] = [ SSMAX 0 ] [-SNL CSL ] [ 0 H ] [ SNR CSR ] [ 0 SSMIN ].
pure subroutine, public	la_dlaswp (n, a, lda, k1, k2, ipiv, incx)
	DLASWP: performs a series of row interchanges on the matrix A. One row interchange is initiated for each of rows K1 through K2 of A.
pure subroutine, public	la_dlasy2 (ltranl, ltranr, isgn, n1, n2, tl, ldtl, tr, ldtr, b, ldb, scale, x, ldx, xnorm, info)
	DLASY2: solves for the N1 by N2 matrix X, 1 <= N1,N2 <= 2, in op(TL)*X + ISGN*X*op(TR) = SCALE*B, where TL is N1 by N1, TR is N2 by N2, B is N1 by N2, and ISGN = 1 or -1. op(T) = T or T**T, where T**T denotes the transpose of T.
pure subroutine, public	la_dlasyf (uplo, n, nb, kb, a, lda, ipiv, w, ldw, info)
	DLASYF: computes a partial factorization of a real symmetric matrix A using the Bunch-Kaufman diagonal pivoting method. The partial factorization has the form: A = ( I U12 ) ( A11 0 ) ( I 0 ) if UPLO = 'U', or: ( 0 U22 ) ( 0 D ) ( U12**T U22**T ) A = ( L11 0 ) ( D 0 ) ( L11**T L21**T ) if UPLO = 'L' ( L21 I ) ( 0 A22 ) ( 0 I ) where the order of D is at most NB. The actual order is returned in the argument KB, and is either NB or NB-1, or N if N <= NB. DLASYF is an auxiliary routine called by DSYTRF. It uses blocked code (calling Level 3 BLAS) to update the submatrix A11 (if UPLO = 'U') or A22 (if UPLO = 'L').
pure subroutine, public	la_dlasyf_rk (uplo, n, nb, kb, a, lda, e, ipiv, w, ldw, info)
	DLASYF_RK: computes a partial factorization of a real symmetric matrix A using the bounded Bunch-Kaufman (rook) diagonal pivoting method. The partial factorization has the form: A = ( I U12 ) ( A11 0 ) ( I 0 ) if UPLO = 'U', or: ( 0 U22 ) ( 0 D ) ( U12**T U22**T ) A = ( L11 0 ) ( D 0 ) ( L11**T L21**T ) if UPLO = 'L', ( L21 I ) ( 0 A22 ) ( 0 I ) where the order of D is at most NB. The actual order is returned in the argument KB, and is either NB or NB-1, or N if N <= NB. DLASYF_RK is an auxiliary routine called by DSYTRF_RK. It uses blocked code (calling Level 3 BLAS) to update the submatrix A11 (if UPLO = 'U') or A22 (if UPLO = 'L').
pure subroutine, public	la_dlasyf_rook (uplo, n, nb, kb, a, lda, ipiv, w, ldw, info)
	DLASYF_ROOK: computes a partial factorization of a real symmetric matrix A using the bounded Bunch-Kaufman ("rook") diagonal pivoting method. The partial factorization has the form: A = ( I U12 ) ( A11 0 ) ( I 0 ) if UPLO = 'U', or: ( 0 U22 ) ( 0 D ) ( U12**T U22**T ) A = ( L11 0 ) ( D 0 ) ( L11**T L21**T ) if UPLO = 'L' ( L21 I ) ( 0 A22 ) ( 0 I ) where the order of D is at most NB. The actual order is returned in the argument KB, and is either NB or NB-1, or N if N <= NB. DLASYF_ROOK is an auxiliary routine called by DSYTRF_ROOK. It uses blocked code (calling Level 3 BLAS) to update the submatrix A11 (if UPLO = 'U') or A22 (if UPLO = 'L').
pure subroutine, public	la_dlat2s (uplo, n, a, lda, sa, ldsa, info)
	DLAT2S: converts a DOUBLE PRECISION triangular matrix, SA, to a SINGLE PRECISION triangular matrix, A. RMAX is the overflow for the SINGLE PRECISION arithmetic DLAS2S checks that all the entries of A are between -RMAX and RMAX. If not the conversion is aborted and a flag is raised. This is an auxiliary routine so there is no argument checking.
pure subroutine, public	la_dlatbs (uplo, trans, diag, normin, n, kd, ab, ldab, x, scale, cnorm, info)
	DLATBS: solves one of the triangular systems A *x = s*b or A**T*x = s*b with scaling to prevent overflow, where A is an upper or lower triangular band matrix. Here A**T denotes the transpose of A, x and b are n-element vectors, and s is a scaling factor, usually less than or equal to 1, chosen so that the components of x will be less than the overflow threshold. If the unscaled problem will not cause overflow, the Level 2 BLAS routine DTBSV is called. If the matrix A is singular (A(j,j) = 0 for some j), then s is set to 0 and a non-trivial solution to A*x = 0 is returned.
pure subroutine, public	la_dlatps (uplo, trans, diag, normin, n, ap, x, scale, cnorm, info)
	DLATPS: solves one of the triangular systems A *x = s*b or A**T*x = s*b with scaling to prevent overflow, where A is an upper or lower triangular matrix stored in packed form. Here A**T denotes the transpose of A, x and b are n-element vectors, and s is a scaling factor, usually less than or equal to 1, chosen so that the components of x will be less than the overflow threshold. If the unscaled problem will not cause overflow, the Level 2 BLAS routine DTPSV is called. If the matrix A is singular (A(j,j) = 0 for some j), then s is set to 0 and a non-trivial solution to A*x = 0 is returned.
pure subroutine, public	la_dlatrs (uplo, trans, diag, normin, n, a, lda, x, scale, cnorm, info)
	DLATRS: solves one of the triangular systems A *x = s*b or A**T *x = s*b with scaling to prevent overflow. Here A is an upper or lower triangular matrix, A**T denotes the transpose of A, x and b are n-element vectors, and s is a scaling factor, usually less than or equal to 1, chosen so that the components of x will be less than the overflow threshold. If the unscaled problem will not cause overflow, the Level 2 BLAS routine DTRSV is called. If the matrix A is singular (A(j,j) = 0 for some j), then s is set to 0 and a non-trivial solution to A*x = 0 is returned.
pure subroutine, public	la_dlauu2 (uplo, n, a, lda, info)
	DLAUU2: computes the product U * U**T or L**T * L, where the triangular factor U or L is stored in the upper or lower triangular part of the array A. If UPLO = 'U' or 'u' then the upper triangle of the result is stored, overwriting the factor U in A. If UPLO = 'L' or 'l' then the lower triangle of the result is stored, overwriting the factor L in A. This is the unblocked form of the algorithm, calling Level 2 BLAS.
pure subroutine, public	la_dlauum (uplo, n, a, lda, info)
	DLAUUM: computes the product U * U**T or L**T * L, where the triangular factor U or L is stored in the upper or lower triangular part of the array A. If UPLO = 'U' or 'u' then the upper triangle of the result is stored, overwriting the factor U in A. If UPLO = 'L' or 'l' then the lower triangle of the result is stored, overwriting the factor L in A. This is the blocked form of the algorithm, calling Level 3 BLAS.
pure subroutine, public	la_dorbdb6 (m1, m2, n, x1, incx1, x2, incx2, q1, ldq1, q2, ldq2, work, lwork, info)
	DORBDB6: orthogonalizes the column vector X = [ X1 ] [ X2 ] with respect to the columns of Q = [ Q1 ] . [ Q2 ] The columns of Q must be orthonormal. If the projection is zero according to Kahan's "twice is enough" criterion, then the zero vector is returned.
pure subroutine, public	la_dorg2l (m, n, k, a, lda, tau, work, info)
	DORG2L: generates an m by n real matrix Q with orthonormal columns, which is defined as the last n columns of a product of k elementary reflectors of order m Q = H(k) . . . H(2) H(1) as returned by DGEQLF.
pure subroutine, public	la_dorg2r (m, n, k, a, lda, tau, work, info)
	DORG2R: generates an m by n real matrix Q with orthonormal columns, which is defined as the first n columns of a product of k elementary reflectors of order m Q = H(1) H(2) . . . H(k) as returned by DGEQRF.
pure subroutine, public	la_dorgl2 (m, n, k, a, lda, tau, work, info)
	DORGL2: generates an m by n real matrix Q with orthonormal rows, which is defined as the first m rows of a product of k elementary reflectors of order n Q = H(k) . . . H(2) H(1) as returned by DGELQF.
pure subroutine, public	la_dorglq (m, n, k, a, lda, tau, work, lwork, info)
	DORGLQ: generates an M-by-N real matrix Q with orthonormal rows, which is defined as the first M rows of a product of K elementary reflectors of order N Q = H(k) . . . H(2) H(1) as returned by DGELQF.
pure subroutine, public	la_dorgql (m, n, k, a, lda, tau, work, lwork, info)
	DORGQL: generates an M-by-N real matrix Q with orthonormal columns, which is defined as the last N columns of a product of K elementary reflectors of order M Q = H(k) . . . H(2) H(1) as returned by DGEQLF.
pure subroutine, public	la_dorgqr (m, n, k, a, lda, tau, work, lwork, info)
	DORGQR: generates an M-by-N real matrix Q with orthonormal columns, which is defined as the first N columns of a product of K elementary reflectors of order M Q = H(1) H(2) . . . H(k) as returned by DGEQRF.
pure subroutine, public	la_dorgr2 (m, n, k, a, lda, tau, work, info)
	DORGR2: generates an m by n real matrix Q with orthonormal rows, which is defined as the last m rows of a product of k elementary reflectors of order n Q = H(1) H(2) . . . H(k) as returned by DGERQF.
pure subroutine, public	la_dorgrq (m, n, k, a, lda, tau, work, lwork, info)
	DORGRQ: generates an M-by-N real matrix Q with orthonormal rows, which is defined as the last M rows of a product of K elementary reflectors of order N Q = H(1) H(2) . . . H(k) as returned by DGERQF.
pure subroutine, public	la_dorgtsqr_row (m, n, mb, nb, a, lda, t, ldt, work, lwork, info)
	DORGTSQR_ROW: generates an M-by-N real matrix Q_out with orthonormal columns from the output of DLATSQR. These N orthonormal columns are the first N columns of a product of complex unitary matrices Q(k)_in of order M, which are returned by DLATSQR in a special format. Q_out = first_N_columns_of( Q(1)_in * Q(2)_in * ... * Q(k)_in ). The input matrices Q(k)_in are stored in row and column blocks in A. See the documentation of DLATSQR for more details on the format of Q(k)_in, where each Q(k)_in is represented by block Householder transformations. This routine calls an auxiliary routine DLARFB_GETT, where the computation is performed on each individual block. The algorithm first sweeps NB-sized column blocks from the right to left starting in the bottom row block and continues to the top row block (hence _ROW in the routine name). This sweep is in reverse order of the order in which DLATSQR generates the output blocks.
pure subroutine, public	la_dorm22 (side, trans, m, n, n1, n2, q, ldq, c, ldc, work, lwork, info)
pure subroutine, public	la_dorm2l (side, trans, m, n, k, a, lda, tau, c, ldc, work, info)
	DORM2L: overwrites the general real m by n matrix C with Q * C if SIDE = 'L' and TRANS = 'N', or Q**T * C if SIDE = 'L' and TRANS = 'T', or C * Q if SIDE = 'R' and TRANS = 'N', or C * Q**T if SIDE = 'R' and TRANS = 'T', where Q is a real orthogonal matrix defined as the product of k elementary reflectors Q = H(k) . . . H(2) H(1) as returned by DGEQLF. Q is of order m if SIDE = 'L' and of order n if SIDE = 'R'.
pure subroutine, public	la_dorm2r (side, trans, m, n, k, a, lda, tau, c, ldc, work, info)
	DORM2R: overwrites the general real m by n matrix C with Q * C if SIDE = 'L' and TRANS = 'N', or Q**T* C if SIDE = 'L' and TRANS = 'T', or C * Q if SIDE = 'R' and TRANS = 'N', or C * Q**T if SIDE = 'R' and TRANS = 'T', where Q is a real orthogonal matrix defined as the product of k elementary reflectors Q = H(1) H(2) . . . H(k) as returned by DGEQRF. Q is of order m if SIDE = 'L' and of order n if SIDE = 'R'.
pure subroutine, public	la_dorml2 (side, trans, m, n, k, a, lda, tau, c, ldc, work, info)
	DORML2: overwrites the general real m by n matrix C with Q * C if SIDE = 'L' and TRANS = 'N', or Q**T* C if SIDE = 'L' and TRANS = 'T', or C * Q if SIDE = 'R' and TRANS = 'N', or C * Q**T if SIDE = 'R' and TRANS = 'T', where Q is a real orthogonal matrix defined as the product of k elementary reflectors Q = H(k) . . . H(2) H(1) as returned by DGELQF. Q is of order m if SIDE = 'L' and of order n if SIDE = 'R'.
pure subroutine, public	la_dormlq (side, trans, m, n, k, a, lda, tau, c, ldc, work, lwork, info)
	DORMLQ: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q * C C * Q TRANS = 'T': Q**T * C C * Q**T where Q is a real orthogonal matrix defined as the product of k elementary reflectors Q = H(k) . . . H(2) H(1) as returned by DGELQF. Q is of order M if SIDE = 'L' and of order N if SIDE = 'R'.
pure subroutine, public	la_dormql (side, trans, m, n, k, a, lda, tau, c, ldc, work, lwork, info)
	DORMQL: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q * C C * Q TRANS = 'T': Q**T * C C * Q**T where Q is a real orthogonal matrix defined as the product of k elementary reflectors Q = H(k) . . . H(2) H(1) as returned by DGEQLF. Q is of order M if SIDE = 'L' and of order N if SIDE = 'R'.
pure subroutine, public	la_dormqr (side, trans, m, n, k, a, lda, tau, c, ldc, work, lwork, info)
	DORMQR: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q * C C * Q TRANS = 'T': Q**T * C C * Q**T where Q is a real orthogonal matrix defined as the product of k elementary reflectors Q = H(1) H(2) . . . H(k) as returned by DGEQRF. Q is of order M if SIDE = 'L' and of order N if SIDE = 'R'.
pure subroutine, public	la_dormr2 (side, trans, m, n, k, a, lda, tau, c, ldc, work, info)
	DORMR2: overwrites the general real m by n matrix C with Q * C if SIDE = 'L' and TRANS = 'N', or Q**T* C if SIDE = 'L' and TRANS = 'T', or C * Q if SIDE = 'R' and TRANS = 'N', or C * Q**T if SIDE = 'R' and TRANS = 'T', where Q is a real orthogonal matrix defined as the product of k elementary reflectors Q = H(1) H(2) . . . H(k) as returned by DGERQF. Q is of order m if SIDE = 'L' and of order n if SIDE = 'R'.
pure subroutine, public	la_dormr3 (side, trans, m, n, k, l, a, lda, tau, c, ldc, work, info)
	DORMR3: overwrites the general real m by n matrix C with Q * C if SIDE = 'L' and TRANS = 'N', or Q**T* C if SIDE = 'L' and TRANS = 'C', or C * Q if SIDE = 'R' and TRANS = 'N', or C * Q**T if SIDE = 'R' and TRANS = 'C', where Q is a real orthogonal matrix defined as the product of k elementary reflectors Q = H(1) H(2) . . . H(k) as returned by DTZRZF. Q is of order m if SIDE = 'L' and of order n if SIDE = 'R'.
pure subroutine, public	la_dormrq (side, trans, m, n, k, a, lda, tau, c, ldc, work, lwork, info)
	DORMRQ: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q * C C * Q TRANS = 'T': Q**T * C C * Q**T where Q is a real orthogonal matrix defined as the product of k elementary reflectors Q = H(1) H(2) . . . H(k) as returned by DGERQF. Q is of order M if SIDE = 'L' and of order N if SIDE = 'R'.
pure subroutine, public	la_dormrz (side, trans, m, n, k, l, a, lda, tau, c, ldc, work, lwork, info)
	DORMRZ: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q * C C * Q TRANS = 'T': Q**T * C C * Q**T where Q is a real orthogonal matrix defined as the product of k elementary reflectors Q = H(1) H(2) . . . H(k) as returned by DTZRZF. Q is of order M if SIDE = 'L' and of order N if SIDE = 'R'.
pure subroutine, public	la_dpbequ (uplo, n, kd, ab, ldab, s, scond, amax, info)
	DPBEQU: computes row and column scalings intended to equilibrate a symmetric positive definite band matrix A and reduce its condition number (with respect to the two-norm). S contains the scale factors, S(i) = 1/sqrt(A(i,i)), chosen so that the scaled matrix B with elements B(i,j) = S(i)*A(i,j)*S(j) has ones on the diagonal. This choice of S puts the condition number of B within a factor N of the smallest possible condition number over all possible diagonal scalings.
pure subroutine, public	la_dpbstf (uplo, n, kd, ab, ldab, info)
	DPBSTF: computes a split Cholesky factorization of a real symmetric positive definite band matrix A. This routine is designed to be used in conjunction with DSBGST. The factorization has the form A = S**T*S where S is a band matrix of the same bandwidth as A and the following structure: S = ( U ) ( M L ) where U is upper triangular of order m = (n+kd)/2, and L is lower triangular of order n-m.
pure subroutine, public	la_dpbtf2 (uplo, n, kd, ab, ldab, info)
	DPBTF2: computes the Cholesky factorization of a real symmetric positive definite band matrix A. The factorization has the form A = U**T * U , if UPLO = 'U', or A = L * L**T, if UPLO = 'L', where U is an upper triangular matrix, U**T is the transpose of U, and L is lower triangular. This is the unblocked version of the algorithm, calling Level 2 BLAS.
pure subroutine, public	la_dpbtrs (uplo, n, kd, nrhs, ab, ldab, b, ldb, info)
	DPBTRS: solves a system of linear equations A*X = B with a symmetric positive definite band matrix A using the Cholesky factorization A = U**T*U or A = L*L**T computed by DPBTRF.
pure subroutine, public	la_dpoequ (n, a, lda, s, scond, amax, info)
	DPOEQU: computes row and column scalings intended to equilibrate a symmetric positive definite matrix A and reduce its condition number (with respect to the two-norm). S contains the scale factors, S(i) = 1/sqrt(A(i,i)), chosen so that the scaled matrix B with elements B(i,j) = S(i)*A(i,j)*S(j) has ones on the diagonal. This choice of S puts the condition number of B within a factor N of the smallest possible condition number over all possible diagonal scalings.
pure subroutine, public	la_dpoequb (n, a, lda, s, scond, amax, info)
	DPOEQUB: computes row and column scalings intended to equilibrate a symmetric positive definite matrix A and reduce its condition number (with respect to the two-norm). S contains the scale factors, S(i) = 1/sqrt(A(i,i)), chosen so that the scaled matrix B with elements B(i,j) = S(i)*A(i,j)*S(j) has ones on the diagonal. This choice of S puts the condition number of B within a factor N of the smallest possible condition number over all possible diagonal scalings. This routine differs from DPOEQU by restricting the scaling factors to a power of the radix. Barring over- and underflow, scaling by these factors introduces no additional rounding errors. However, the scaled diagonal entries are no longer approximately 1 but lie between sqrt(radix) and 1/sqrt(radix).
pure subroutine, public	la_dpotrs (uplo, n, nrhs, a, lda, b, ldb, info)
	DPOTRS: solves a system of linear equations A*X = B with a symmetric positive definite matrix A using the Cholesky factorization A = U**T*U or A = L*L**T computed by DPOTRF.
pure subroutine, public	la_dppequ (uplo, n, ap, s, scond, amax, info)
	DPPEQU: computes row and column scalings intended to equilibrate a symmetric positive definite matrix A in packed storage and reduce its condition number (with respect to the two-norm). S contains the scale factors, S(i)=1/sqrt(A(i,i)), chosen so that the scaled matrix B with elements B(i,j)=S(i)*A(i,j)*S(j) has ones on the diagonal. This choice of S puts the condition number of B within a factor N of the smallest possible condition number over all possible diagonal scalings.
pure subroutine, public	la_dpptrf (uplo, n, ap, info)
	DPPTRF: computes the Cholesky factorization of a real symmetric positive definite matrix A stored in packed format. The factorization has the form A = U**T * U, if UPLO = 'U', or A = L * L**T, if UPLO = 'L', where U is an upper triangular matrix and L is lower triangular.
pure subroutine, public	la_dpptrs (uplo, n, nrhs, ap, b, ldb, info)
	DPPTRS: solves a system of linear equations A*X = B with a symmetric positive definite matrix A in packed storage using the Cholesky factorization A = U**T*U or A = L*L**T computed by DPPTRF.
pure subroutine, public	la_dptcon (n, d, e, anorm, rcond, work, info)
	DPTCON: computes the reciprocal of the condition number (in the 1-norm) of a real symmetric positive definite tridiagonal matrix using the factorization A = L*D*L**T or A = U**T*D*U computed by DPTTRF. Norm(inv(A)) is computed by a direct method, and the reciprocal of the condition number is computed as RCOND = 1 / (ANORM * norm(inv(A))).
pure subroutine, public	la_dpttrf (n, d, e, info)
	DPTTRF: computes the L*D*L**T factorization of a real symmetric positive definite tridiagonal matrix A. The factorization may also be regarded as having the form A = U**T*D*U.
pure subroutine, public	la_dptts2 (n, nrhs, d, e, b, ldb)
	DPTTS2: solves a tridiagonal system of the form A * X = B using the L*D*L**T factorization of A computed by DPTTRF. D is a diagonal matrix specified in the vector D, L is a unit bidiagonal matrix whose subdiagonal is specified in the vector E, and X and B are N by NRHS matrices.
pure subroutine, public	la_drscl (n, sa, sx, incx)
	DRSCL: multiplies an n-element real vector x by the real scalar 1/a. This is done without overflow or underflow as long as the final result x/a does not overflow or underflow.
pure subroutine, public	la_dsbgst (vect, uplo, n, ka, kb, ab, ldab, bb, ldbb, x, ldx, work, info)
	DSBGST: reduces a real symmetric-definite banded generalized eigenproblem A*x = lambda*B*x to standard form C*y = lambda*y, such that C has the same bandwidth as A. B must have been previously factorized as S**T*S by DPBSTF, using a split Cholesky factorization. A is overwritten by C = X**T*A*X, where X = S**(-1)*Q and Q is an orthogonal matrix chosen to preserve the bandwidth of A.
pure subroutine, public	la_dsbtrd (vect, uplo, n, kd, ab, ldab, d, e, q, ldq, work, info)
	DSBTRD: reduces a real symmetric band matrix A to symmetric tridiagonal form T by an orthogonal similarity transformation: Q**T * A * Q = T.
pure subroutine, public	la_dsfrk (transr, uplo, trans, n, k, alpha, a, lda, beta, c)
	Level 3 BLAS like routine for C in RFP Format. DSFRK: performs one of the symmetric rank–k operations C := alpha*A*A**T + beta*C, or C := alpha*A**T*A + beta*C, where alpha and beta are real scalars, C is an n–by–n symmetric matrix and A is an n–by–k matrix in the first case and a k–by–n matrix in the second case.
pure subroutine, public	la_dspgst (itype, uplo, n, ap, bp, info)
	DSPGST: reduces a real symmetric-definite generalized eigenproblem to standard form, using packed storage. If ITYPE = 1, the problem is A*x = lambda*B*x, and A is overwritten by inv(U**T)*A*inv(U) or inv(L)*A*inv(L**T) If ITYPE = 2 or 3, the problem is A*B*x = lambda*x or B*A*x = lambda*x, and A is overwritten by U*A*U**T or L**T*A*L. B must have been previously factorized as U**T*U or L*L**T by DPPTRF.
pure subroutine, public	la_dsptrf (uplo, n, ap, ipiv, info)
	DSPTRF: computes the factorization of a real symmetric matrix A stored in packed format using the Bunch-Kaufman diagonal pivoting method: A = U*D*U**T or A = L*D*L**T where U (or L) is a product of permutation and unit upper (lower) triangular matrices, and D is symmetric and block diagonal with 1-by-1 and 2-by-2 diagonal blocks.
pure subroutine, public	la_dsptri (uplo, n, ap, ipiv, work, info)
	DSPTRI: computes the inverse of a real symmetric indefinite matrix A in packed storage using the factorization A = U*D*U**T or A = L*D*L**T computed by DSPTRF.
pure subroutine, public	la_dsptrs (uplo, n, nrhs, ap, ipiv, b, ldb, info)
	DSPTRS: solves a system of linear equations A*X = B with a real symmetric matrix A stored in packed format using the factorization A = U*D*U**T or A = L*D*L**T computed by DSPTRF.
pure subroutine, public	la_dstebz (range, order, n, vl, vu, il, iu, abstol, d, e, m, nsplit, w, iblock, isplit, work, iwork, info)
	DSTEBZ: computes the eigenvalues of a symmetric tridiagonal matrix T. The user may ask for all eigenvalues, all eigenvalues in the half-open interval (VL, VU], or the IL-th through IU-th eigenvalues. To avoid overflow, the matrix must be scaled so that its largest element is no greater than overflow**(1/2) * underflow**(1/4) in absolute value, and for greatest accuracy, it should not be much smaller than that. See W. Kahan "Accurate Eigenvalues of a Symmetric Tridiagonal Matrix", Report CS41, Computer Science Dept., Stanford University, July 21, 1966.
pure subroutine, public	la_dsyconv (uplo, way, n, a, lda, ipiv, e, info)
	DSYCONV: convert A given by TRF into L and D and vice-versa. Get Non-diag elements of D (returned in workspace) and apply or reverse permutation done in TRF.
pure subroutine, public	la_dsyconvf (uplo, way, n, a, lda, e, ipiv, info)
	If parameter WAY = 'C': DSYCONVF: converts the factorization output format used in DSYTRF provided on entry in parameter A into the factorization output format used in DSYTRF_RK (or DSYTRF_BK) that is stored on exit in parameters A and E. It also converts in place details of the intechanges stored in IPIV from the format used in DSYTRF into the format used in DSYTRF_RK (or DSYTRF_BK). If parameter WAY = 'R': DSYCONVF performs the conversion in reverse direction, i.e. converts the factorization output format used in DSYTRF_RK (or DSYTRF_BK) provided on entry in parameters A and E into the factorization output format used in DSYTRF that is stored on exit in parameter A. It also converts in place details of the intechanges stored in IPIV from the format used in DSYTRF_RK (or DSYTRF_BK) into the format used in DSYTRF.
pure subroutine, public	la_dsyconvf_rook (uplo, way, n, a, lda, e, ipiv, info)
	If parameter WAY = 'C': DSYCONVF_ROOK: converts the factorization output format used in DSYTRF_ROOK provided on entry in parameter A into the factorization output format used in DSYTRF_RK (or DSYTRF_BK) that is stored on exit in parameters A and E. IPIV format for DSYTRF_ROOK and DSYTRF_RK (or DSYTRF_BK) is the same and is not converted. If parameter WAY = 'R': DSYCONVF_ROOK performs the conversion in reverse direction, i.e. converts the factorization output format used in DSYTRF_RK (or DSYTRF_BK) provided on entry in parameters A and E into the factorization output format used in DSYTRF_ROOK that is stored on exit in parameter A. IPIV format for DSYTRF_ROOK and DSYTRF_RK (or DSYTRF_BK) is the same and is not converted.
pure subroutine, public	la_dsyequb (uplo, n, a, lda, s, scond, amax, work, info)
	DSYEQUB: computes row and column scalings intended to equilibrate a symmetric matrix A (with respect to the Euclidean norm) and reduce its condition number. The scale factors S are computed by the BIN algorithm (see references) so that the scaled matrix B with elements B(i,j) = S(i)*A(i,j)*S(j) has a condition number within a factor N of the smallest possible condition number over all possible diagonal scalings.
pure subroutine, public	la_dsygs2 (itype, uplo, n, a, lda, b, ldb, info)
	DSYGS2: reduces a real symmetric-definite generalized eigenproblem to standard form. If ITYPE = 1, the problem is A*x = lambda*B*x, and A is overwritten by inv(U**T)*A*inv(U) or inv(L)*A*inv(L**T) If ITYPE = 2 or 3, the problem is A*B*x = lambda*x or B*A*x = lambda*x, and A is overwritten by U*A*U**T or L**T *A*L. B must have been previously factorized as U**T *U or L*L**T by DPOTRF.
pure subroutine, public	la_dsygst (itype, uplo, n, a, lda, b, ldb, info)
	DSYGST: reduces a real symmetric-definite generalized eigenproblem to standard form. If ITYPE = 1, the problem is A*x = lambda*B*x, and A is overwritten by inv(U**T)*A*inv(U) or inv(L)*A*inv(L**T) If ITYPE = 2 or 3, the problem is A*B*x = lambda*x or B*A*x = lambda*x, and A is overwritten by U*A*U**T or L**T*A*L. B must have been previously factorized as U**T*U or L*L**T by DPOTRF.
pure subroutine, public	la_dsyswapr (uplo, n, a, lda, i1, i2)
	DSYSWAPR: applies an elementary permutation on the rows and the columns of a symmetric matrix.
pure subroutine, public	la_dsytf2_rk (uplo, n, a, lda, e, ipiv, info)
	DSYTF2_RK: computes the factorization of a real symmetric matrix A using the bounded Bunch-Kaufman (rook) diagonal pivoting method: A = P*U*D*(U**T)*(P**T) or A = P*L*D*(L**T)*(P**T), where U (or L) is unit upper (or lower) triangular matrix, U**T (or L**T) is the transpose of U (or L), P is a permutation matrix, P**T is the transpose of P, and D is symmetric and block diagonal with 1-by-1 and 2-by-2 diagonal blocks. This is the unblocked version of the algorithm, calling Level 2 BLAS. For more information see Further Details section.
pure subroutine, public	la_dsytf2_rook (uplo, n, a, lda, ipiv, info)
	DSYTF2_ROOK: computes the factorization of a real symmetric matrix A using the bounded Bunch-Kaufman ("rook") diagonal pivoting method: A = U*D*U**T or A = L*D*L**T where U (or L) is a product of permutation and unit upper (lower) triangular matrices, U**T is the transpose of U, and D is symmetric and block diagonal with 1-by-1 and 2-by-2 diagonal blocks. This is the unblocked version of the algorithm, calling Level 2 BLAS.
pure subroutine, public	la_dsytrf_rk (uplo, n, a, lda, e, ipiv, work, lwork, info)
	DSYTRF_RK: computes the factorization of a real symmetric matrix A using the bounded Bunch-Kaufman (rook) diagonal pivoting method: A = P*U*D*(U**T)*(P**T) or A = P*L*D*(L**T)*(P**T), where U (or L) is unit upper (or lower) triangular matrix, U**T (or L**T) is the transpose of U (or L), P is a permutation matrix, P**T is the transpose of P, and D is symmetric and block diagonal with 1-by-1 and 2-by-2 diagonal blocks. This is the blocked version of the algorithm, calling Level 3 BLAS. For more information see Further Details section.
pure subroutine, public	la_dsytrf_rook (uplo, n, a, lda, ipiv, work, lwork, info)
	DSYTRF_ROOK: computes the factorization of a real symmetric matrix A using the bounded Bunch-Kaufman ("rook") diagonal pivoting method. The form of the factorization is A = U*D*U**T or A = L*D*L**T where U (or L) is a product of permutation and unit upper (lower) triangular matrices, and D is symmetric and block diagonal with 1-by-1 and 2-by-2 diagonal blocks. This is the blocked version of the algorithm, calling Level 3 BLAS.
pure subroutine, public	la_dsytri (uplo, n, a, lda, ipiv, work, info)
	DSYTRI: computes the inverse of a real symmetric indefinite matrix A using the factorization A = U*D*U**T or A = L*D*L**T computed by DSYTRF.
pure subroutine, public	la_dsytri_rook (uplo, n, a, lda, ipiv, work, info)
	DSYTRI_ROOK: computes the inverse of a real symmetric matrix A using the factorization A = U*D*U**T or A = L*D*L**T computed by DSYTRF_ROOK.
pure subroutine, public	la_dsytrs (uplo, n, nrhs, a, lda, ipiv, b, ldb, info)
	DSYTRS: solves a system of linear equations A*X = B with a real symmetric matrix A using the factorization A = U*D*U**T or A = L*D*L**T computed by DSYTRF.
pure subroutine, public	la_dsytrs2 (uplo, n, nrhs, a, lda, ipiv, b, ldb, work, info)
	DSYTRS2: solves a system of linear equations A*X = B with a real symmetric matrix A using the factorization A = U*D*U**T or A = L*D*L**T computed by DSYTRF and converted by DSYCONV.
pure subroutine, public	la_dsytrs_3 (uplo, n, nrhs, a, lda, e, ipiv, b, ldb, info)
	DSYTRS_3: solves a system of linear equations A * X = B with a real symmetric matrix A using the factorization computed by DSYTRF_RK or DSYTRF_BK: A = P*U*D*(U**T)*(P**T) or A = P*L*D*(L**T)*(P**T), where U (or L) is unit upper (or lower) triangular matrix, U**T (or L**T) is the transpose of U (or L), P is a permutation matrix, P**T is the transpose of P, and D is symmetric and block diagonal with 1-by-1 and 2-by-2 diagonal blocks. This algorithm is using Level 3 BLAS.
pure subroutine, public	la_dsytrs_aa (uplo, n, nrhs, a, lda, ipiv, b, ldb, work, lwork, info)
	DSYTRS_AA: solves a system of linear equations A*X = B with a real symmetric matrix A using the factorization A = U**T*T*U or A = L*T*L**T computed by DSYTRF_AA.
pure subroutine, public	la_dsytrs_rook (uplo, n, nrhs, a, lda, ipiv, b, ldb, info)
	DSYTRS_ROOK: solves a system of linear equations A*X = B with a real symmetric matrix A using the factorization A = U*D*U**T or A = L*D*L**T computed by DSYTRF_ROOK.
pure subroutine, public	la_dtbrfs (uplo, trans, diag, n, kd, nrhs, ab, ldab, b, ldb, x, ldx, ferr, berr, work, iwork, info)
	DTBRFS: provides error bounds and backward error estimates for the solution to a system of linear equations with a triangular band coefficient matrix. The solution matrix X must be computed by DTBTRS or some other means before entering this routine. DTBRFS does not do iterative refinement because doing so cannot improve the backward error.
pure subroutine, public	la_dtbtrs (uplo, trans, diag, n, kd, nrhs, ab, ldab, b, ldb, info)
	DTBTRS: solves a triangular system of the form A * X = B or A**T * X = B, where A is a triangular band matrix of order N, and B is an N-by NRHS matrix. A check is made to verify that A is nonsingular.
pure subroutine, public	la_dtfsm (transr, side, uplo, trans, diag, m, n, alpha, a, b, ldb)
	Level 3 BLAS like routine for A in RFP Format. DTFSM: solves the matrix equation op( A )*X = alpha*B or X*op( A ) = alpha*B where alpha is a scalar, X and B are m by n matrices, A is a unit, or non-unit, upper or lower triangular matrix and op( A ) is one of op( A ) = A or op( A ) = A**T. A is in Rectangular Full Packed (RFP) Format. The matrix X is overwritten on B.
pure subroutine, public	la_dtfttp (transr, uplo, n, arf, ap, info)
	DTFTTP: copies a triangular matrix A from rectangular full packed format (TF) to standard packed format (TP).
pure subroutine, public	la_dtfttr (transr, uplo, n, arf, a, lda, info)
	DTFTTR: copies a triangular matrix A from rectangular full packed format (TF) to standard full format (TR).
pure subroutine, public	la_dtprfb (side, trans, direct, storev, m, n, k, l, v, ldv, t, ldt, a, lda, b, ldb, work, ldwork)
	DTPRFB: applies a real "triangular-pentagonal" block reflector H or its transpose H**T to a real matrix C, which is composed of two blocks A and B, either from the left or right.
pure subroutine, public	la_dtprfs (uplo, trans, diag, n, nrhs, ap, b, ldb, x, ldx, ferr, berr, work, iwork, info)
	DTPRFS: provides error bounds and backward error estimates for the solution to a system of linear equations with a triangular packed coefficient matrix. The solution matrix X must be computed by DTPTRS or some other means before entering this routine. DTPRFS does not do iterative refinement because doing so cannot improve the backward error.
pure subroutine, public	la_dtptri (uplo, diag, n, ap, info)
	DTPTRI: computes the inverse of a real upper or lower triangular matrix A stored in packed format.
pure subroutine, public	la_dtptrs (uplo, trans, diag, n, nrhs, ap, b, ldb, info)
	DTPTRS: solves a triangular system of the form A * X = B or A**T * X = B, where A is a triangular matrix of order N stored in packed format, and B is an N-by-NRHS matrix. A check is made to verify that A is nonsingular.
pure subroutine, public	la_dtpttf (transr, uplo, n, ap, arf, info)
	DTPTTF: copies a triangular matrix A from standard packed format (TP) to rectangular full packed format (TF).
pure subroutine, public	la_dtpttr (uplo, n, ap, a, lda, info)
	DTPTTR: copies a triangular matrix A from standard packed format (TP) to standard full format (TR).
pure subroutine, public	la_dtrrfs (uplo, trans, diag, n, nrhs, a, lda, b, ldb, x, ldx, ferr, berr, work, iwork, info)
	DTRRFS: provides error bounds and backward error estimates for the solution to a system of linear equations with a triangular coefficient matrix. The solution matrix X must be computed by DTRTRS or some other means before entering this routine. DTRRFS does not do iterative refinement because doing so cannot improve the backward error.
pure subroutine, public	la_dtrti2 (uplo, diag, n, a, lda, info)
	DTRTI2: computes the inverse of a real upper or lower triangular matrix. This is the Level 2 BLAS version of the algorithm.
pure subroutine, public	la_dtrtri (uplo, diag, n, a, lda, info)
	DTRTRI: computes the inverse of a real upper or lower triangular matrix A. This is the Level 3 BLAS version of the algorithm.
pure subroutine, public	la_dtrtrs (uplo, trans, diag, n, nrhs, a, lda, b, ldb, info)
	DTRTRS: solves a triangular system of the form A * X = B or A**T * X = B, where A is a triangular matrix of order N, and B is an N-by-NRHS matrix. A check is made to verify that A is nonsingular.
pure subroutine, public	la_dtrttf (transr, uplo, n, a, lda, arf, info)
	DTRTTF: copies a triangular matrix A from standard full format (TR) to rectangular full packed format (TF) .
pure subroutine, public	la_dtrttp (uplo, n, a, lda, ap, info)
	DTRTTP: copies a triangular matrix A from full format (TR) to standard packed format (TP).
pure real(dp) function, public	la_dzsum1 (n, cx, incx)
	DZSUM1: takes the sum of the absolute values of a complex vector and returns a double precision result. Based on DZASUM from the Level 1 BLAS. The change is to use the 'genuine' absolute value.
pure subroutine, public	la_dlag2q (m, n, sa, ldsa, a, lda, info)
	DLAG2Q: converts a SINGLE PRECISION matrix, SA, to a DOUBLE PRECISION matrix, A. Note that while it is possible to overflow while converting from double to single, it is not possible to overflow when converting from single to double. This is an auxiliary routine so there is no argument checking.
pure subroutine, public	la_dbbcsd (jobu1, jobu2, jobv1t, jobv2t, trans, m, p, q, theta, phi, u1, ldu1, u2, ldu2, v1t, ldv1t, v2t, ldv2t, b11d, b11e, b12d, b12e, b21d, b21e, b22d, b22e, work, lwork, info)
	DBBCSD: computes the CS decomposition of an orthogonal matrix in bidiagonal-block form, [ B11 | B12 0 0 ] [ 0 | 0 -I 0 ] X = [-------------—] [ B21 | B22 0 0 ] [ 0 | 0 0 I ] [ C | -S 0 0 ] [ U1 | ] [ 0 | 0 -I 0 ] [ V1 | ]**T = [------—] [------------—] [------—] . [ | U2 ] [ S | C 0 0 ] [ | V2 ] [ 0 | 0 0 I ] X is M-by-M, its top-left block is P-by-Q, and Q must be no larger than P, M-P, or M-Q. (If Q is not the smallest index, then X must be transposed and/or permuted. This can be done in constant time using the TRANS and SIGNS options. See DORCSD for details.) The bidiagonal matrices B11, B12, B21, and B22 are represented implicitly by angles THETA(1:Q) and PHI(1:Q-1). The orthogonal matrices U1, U2, V1T, and V2T are input/output. The input matrices are pre- or post-multiplied by the appropriate singular vector matrices.
pure subroutine, public	la_ddisna (job, m, n, d, sep, info)
	DDISNA: computes the reciprocal condition numbers for the eigenvectors of a real symmetric or complex Hermitian matrix or for the left or right singular vectors of a general m-by-n matrix. The reciprocal condition number is the 'gap' between the corresponding eigenvalue or singular value and the nearest other one. The bound on the error, measured by angle in radians, in the I-th computed vector is given by DLAMCH( 'E' ) * ( ANORM / SEP( I ) ) where ANORM = 2-norm(A) = max( abs( D(j) ) ). SEP(I) is not allowed to be smaller than DLAMCH( 'E' )*ANORM in order to limit the size of the error bound. DDISNA may also be used to compute error bounds for eigenvectors of the generalized symmetric definite eigenproblem.
pure subroutine, public	la_dgbbrd (vect, m, n, ncc, kl, ku, ab, ldab, d, e, q, ldq, pt, ldpt, c, ldc, work, info)
	DGBBRD: reduces a real general m-by-n band matrix A to upper bidiagonal form B by an orthogonal transformation: Q**T * A * P = B. The routine computes B, and optionally forms Q or P**T, or computes Q**T*C for a given matrix C.
pure subroutine, public	la_dgbcon (norm, n, kl, ku, ab, ldab, ipiv, anorm, rcond, work, iwork, info)
	DGBCON: estimates the reciprocal of the condition number of a real general band matrix A, in either the 1-norm or the infinity-norm, using the LU factorization computed by DGBTRF. An estimate is obtained for norm(inv(A)), and the reciprocal of the condition number is computed as RCOND = 1 / ( norm(A) * norm(inv(A)) ).
pure subroutine, public	la_dgbequ (m, n, kl, ku, ab, ldab, r, c, rowcnd, colcnd, amax, info)
	DGBEQU: computes row and column scalings intended to equilibrate an M-by-N band matrix A and reduce its condition number. R returns the row scale factors and C the column scale factors, chosen to try to make the largest element in each row and column of the matrix B with elements B(i,j)=R(i)*A(i,j)*C(j) have absolute value 1. R(i) and C(j) are restricted to be between SMLNUM = smallest safe number and BIGNUM = largest safe number. Use of these scaling factors is not guaranteed to reduce the condition number of A but works well in practice.
pure subroutine, public	la_dgbequb (m, n, kl, ku, ab, ldab, r, c, rowcnd, colcnd, amax, info)
	DGBEQUB: computes row and column scalings intended to equilibrate an M-by-N matrix A and reduce its condition number. R returns the row scale factors and C the column scale factors, chosen to try to make the largest element in each row and column of the matrix B with elements B(i,j)=R(i)*A(i,j)*C(j) have an absolute value of at most the radix. R(i) and C(j) are restricted to be a power of the radix between SMLNUM = smallest safe number and BIGNUM = largest safe number. Use of these scaling factors is not guaranteed to reduce the condition number of A but works well in practice. This routine differs from DGEEQU by restricting the scaling factors to a power of the radix. Barring over- and underflow, scaling by these factors introduces no additional rounding errors. However, the scaled entries' magnitudes are no longer approximately 1 but lie between sqrt(radix) and 1/sqrt(radix).
pure subroutine, public	la_dgbrfs (trans, n, kl, ku, nrhs, ab, ldab, afb, ldafb, ipiv, b, ldb, x, ldx, ferr, berr, work, iwork, info)
	DGBRFS: improves the computed solution to a system of linear equations when the coefficient matrix is banded, and provides error bounds and backward error estimates for the solution.
pure subroutine, public	la_dgbtrf (m, n, kl, ku, ab, ldab, ipiv, info)
	DGBTRF: computes an LU factorization of a real m-by-n band matrix A using partial pivoting with row interchanges. This is the blocked version of the algorithm, calling Level 3 BLAS.
pure subroutine, public	la_dgecon (norm, n, a, lda, anorm, rcond, work, iwork, info)
	DGECON: estimates the reciprocal of the condition number of a general real matrix A, in either the 1-norm or the infinity-norm, using the LU factorization computed by DGETRF. An estimate is obtained for norm(inv(A)), and the reciprocal of the condition number is computed as RCOND = 1 / ( norm(A) * norm(inv(A)) ).
pure subroutine, public	la_dgeequ (m, n, a, lda, r, c, rowcnd, colcnd, amax, info)
	DGEEQU: computes row and column scalings intended to equilibrate an M-by-N matrix A and reduce its condition number. R returns the row scale factors and C the column scale factors, chosen to try to make the largest element in each row and column of the matrix B with elements B(i,j)=R(i)*A(i,j)*C(j) have absolute value 1. R(i) and C(j) are restricted to be between SMLNUM = smallest safe number and BIGNUM = largest safe number. Use of these scaling factors is not guaranteed to reduce the condition number of A but works well in practice.
pure subroutine, public	la_dgeequb (m, n, a, lda, r, c, rowcnd, colcnd, amax, info)
	DGEEQUB: computes row and column scalings intended to equilibrate an M-by-N matrix A and reduce its condition number. R returns the row scale factors and C the column scale factors, chosen to try to make the largest element in each row and column of the matrix B with elements B(i,j)=R(i)*A(i,j)*C(j) have an absolute value of at most the radix. R(i) and C(j) are restricted to be a power of the radix between SMLNUM = smallest safe number and BIGNUM = largest safe number. Use of these scaling factors is not guaranteed to reduce the condition number of A but works well in practice. This routine differs from DGEEQU by restricting the scaling factors to a power of the radix. Barring over- and underflow, scaling by these factors introduces no additional rounding errors. However, the scaled entries' magnitudes are no longer approximately 1 but lie between sqrt(radix) and 1/sqrt(radix).
pure subroutine, public	la_dgemlqt (side, trans, m, n, k, mb, v, ldv, t, ldt, c, ldc, work, info)
	DGEMLQT: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q C C Q TRANS = 'T': Q**T C C Q**T where Q is a real orthogonal matrix defined as the product of K elementary reflectors: Q = H(1) H(2) . . . H(K) = I - V T V**T generated using the compact WY representation as returned by DGELQT. Q is of order M if SIDE = 'L' and of order N if SIDE = 'R'.
pure subroutine, public	la_dgemqrt (side, trans, m, n, k, nb, v, ldv, t, ldt, c, ldc, work, info)
	DGEMQRT: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q C C Q TRANS = 'T': Q**T C C Q**T where Q is a real orthogonal matrix defined as the product of K elementary reflectors: Q = H(1) H(2) . . . H(K) = I - V T V**T generated using the compact WY representation as returned by DGEQRT. Q is of order M if SIDE = 'L' and of order N if SIDE = 'R'.
pure subroutine, public	la_dgesc2 (n, a, lda, rhs, ipiv, jpiv, scale)
	DGESC2: solves a system of linear equations A * X = scale* RHS with a general N-by-N matrix A using the LU factorization with complete pivoting computed by DGETC2.
pure subroutine, public	la_dgetc2 (n, a, lda, ipiv, jpiv, info)
	DGETC2: computes an LU factorization with complete pivoting of the n-by-n matrix A. The factorization has the form A = P * L * U * Q, where P and Q are permutation matrices, L is lower triangular with unit diagonal elements and U is upper triangular. This is the Level 2 BLAS algorithm.
pure subroutine, public	la_dgetf2 (m, n, a, lda, ipiv, info)
	DGETF2: computes an LU factorization of a general m-by-n matrix A using partial pivoting with row interchanges. The factorization has the form A = P * L * U where P is a permutation matrix, L is lower triangular with unit diagonal elements (lower trapezoidal if m > n), and U is upper triangular (upper trapezoidal if m < n). This is the right-looking Level 2 BLAS version of the algorithm.
pure recursive subroutine, public	la_dgetrf2 (m, n, a, lda, ipiv, info)
	DGETRF2: computes an LU factorization of a general M-by-N matrix A using partial pivoting with row interchanges. The factorization has the form A = P * L * U where P is a permutation matrix, L is lower triangular with unit diagonal elements (lower trapezoidal if m > n), and U is upper triangular (upper trapezoidal if m < n). This is the recursive version of the algorithm. It divides the matrix into four submatrices: [ A11 | A12 ] where A11 is n1 by n1 and A22 is n2 by n2 A = [ --—|--— ] with n1 = min(m,n)/2 [ A21 | A22 ] n2 = n-n1 [ A11 ] The subroutine calls itself to factor [ — ], [ A12 ] [ A12 ] do the swaps on [ — ], solve A12, update A22, [ A22 ] then calls itself to factor A22 and do the swaps on A21.
pure subroutine, public	la_dgetri (n, a, lda, ipiv, work, lwork, info)
	DGETRI: computes the inverse of a matrix using the LU factorization computed by DGETRF. This method inverts U and then computes inv(A) by solving the system inv(A)*L = inv(U) for inv(A).
pure subroutine, public	la_dgetrs (trans, n, nrhs, a, lda, ipiv, b, ldb, info)
	DGETRS: solves a system of linear equations A * X = B or A**T * X = B with a general N-by-N matrix A using the LU factorization computed by DGETRF.
pure subroutine, public	la_dggbal (job, n, a, lda, b, ldb, ilo, ihi, lscale, rscale, work, info)
	DGGBAL: balances a pair of general real matrices (A,B). This involves, first, permuting A and B by similarity transformations to isolate eigenvalues in the first 1 to ILO$-$1 and last IHI+1 to N elements on the diagonal; and second, applying a diagonal similarity transformation to rows and columns ILO to IHI to make the rows and columns as close in norm as possible. Both steps are optional. Balancing may reduce the 1-norm of the matrices, and improve the accuracy of the computed eigenvalues and/or eigenvectors in the generalized eigenvalue problem A*x = lambda*B*x.
pure subroutine, public	la_dgghrd (compq, compz, n, ilo, ihi, a, lda, b, ldb, q, ldq, z, ldz, info)
	DGGHRD: reduces a pair of real matrices (A,B) to generalized upper Hessenberg form using orthogonal transformations, where A is a general matrix and B is upper triangular. The form of the generalized eigenvalue problem is A*x = lambda*B*x, and B is typically made upper triangular by computing its QR factorization and moving the orthogonal matrix Q to the left side of the equation. This subroutine simultaneously reduces A to a Hessenberg matrix H: Q**T*A*Z = H and transforms B to another upper triangular matrix T: Q**T*B*Z = T in order to reduce the problem to its standard form H*y = lambda*T*y where y = Z**T*x. The orthogonal matrices Q and Z are determined as products of Givens rotations. They may either be formed explicitly, or they may be postmultiplied into input matrices Q1 and Z1, so that Q1 * A * Z1**T = (Q1*Q) * H * (Z1*Z)**T Q1 * B * Z1**T = (Q1*Q) * T * (Z1*Z)**T If Q1 is the orthogonal matrix from the QR factorization of B in the original equation A*x = lambda*B*x, then DGGHRD reduces the original problem to generalized Hessenberg form.
pure subroutine, public	la_dgttrs (trans, n, nrhs, dl, d, du, du2, ipiv, b, ldb, info)
	DGTTRS: solves one of the systems of equations A*X = B or A**T*X = B, with a tridiagonal matrix A using the LU factorization computed by DGTTRF.
pure logical(lk) function, public	la_disnan (din)
	DISNAN: returns .TRUE. if its argument is NaN, and .FALSE. otherwise. To be replaced by the Fortran 2003 intrinsic in the future.
subroutine, public	la_dla_gbamv (trans, m, n, kl, ku, alpha, ab, ldab, x, incx, beta, y, incy)
	DLA_GBAMV: performs one of the matrix-vector operations y := alpha*abs(A)*abs(x) + beta*abs(y), or y := alpha*abs(A)**T*abs(x) + beta*abs(y), where alpha and beta are scalars, x and y are vectors and A is an m by n matrix. This function is primarily used in calculating error bounds. To protect against underflow during evaluation, components in the resulting vector are perturbed away from zero by (N+1) times the underflow threshold. To prevent unnecessarily large errors for block-structure embedded in general matrices, "symbolically" zero components are not perturbed. A zero entry is considered "symbolic" if all multiplications involved in computing that entry have at least one zero multiplicand.
real(dp) function, public	la_dla_gbrcond (trans, n, kl, ku, ab, ldab, afb, ldafb, ipiv, cmode, c, info, work, iwork)
	DLA_GBRCOND: Estimates the Skeel condition number of op(A) * op2(C) where op2 is determined by CMODE as follows CMODE = 1 op2(C) = C CMODE = 0 op2(C) = I CMODE = -1 op2(C) = inv(C) The Skeel condition number cond(A) = norminf( |inv(A)||A| ) is computed by computing scaling factors R such that diag(R)*A*op2(C) is row equilibrated and computing the standard infinity-norm condition number.
subroutine, public	la_dla_geamv (trans, m, n, alpha, a, lda, x, incx, beta, y, incy)
	DLA_GEAMV: performs one of the matrix-vector operations y := alpha*abs(A)*abs(x) + beta*abs(y), or y := alpha*abs(A)**T*abs(x) + beta*abs(y), where alpha and beta are scalars, x and y are vectors and A is an m by n matrix. This function is primarily used in calculating error bounds. To protect against underflow during evaluation, components in the resulting vector are perturbed away from zero by (N+1) times the underflow threshold. To prevent unnecessarily large errors for block-structure embedded in general matrices, "symbolically" zero components are not perturbed. A zero entry is considered "symbolic" if all multiplications involved in computing that entry have at least one zero multiplicand.
real(dp) function, public	la_dla_gercond (trans, n, a, lda, af, ldaf, ipiv, cmode, c, info, work, iwork)
	DLA_GERCOND: estimates the Skeel condition number of op(A) * op2(C) where op2 is determined by CMODE as follows CMODE = 1 op2(C) = C CMODE = 0 op2(C) = I CMODE = -1 op2(C) = inv(C) The Skeel condition number cond(A) = norminf( |inv(A)||A| ) is computed by computing scaling factors R such that diag(R)*A*op2(C) is row equilibrated and computing the standard infinity-norm condition number.
pure subroutine, public	la_dla_lin_berr (n, nz, nrhs, res, ayb, berr)
	DLA_LIN_BERR: computes component-wise relative backward error from the formula max(i) ( abs(R(i)) / ( abs(op(A_s))*abs(Y) + abs(B_s) )(i) ) where abs(Z) is the component-wise absolute value of the matrix or vector Z.
real(dp) function, public	la_dla_porcond (uplo, n, a, lda, af, ldaf, cmode, c, info, work, iwork)
	DLA_PORCOND: Estimates the Skeel condition number of op(A) * op2(C) where op2 is determined by CMODE as follows CMODE = 1 op2(C) = C CMODE = 0 op2(C) = I CMODE = -1 op2(C) = inv(C) The Skeel condition number cond(A) = norminf( |inv(A)||A| ) is computed by computing scaling factors R such that diag(R)*A*op2(C) is row equilibrated and computing the standard infinity-norm condition number.
subroutine, public	la_dla_syamv (uplo, n, alpha, a, lda, x, incx, beta, y, incy)
	DLA_SYAMV: performs the matrix-vector operation y := alpha*abs(A)*abs(x) + beta*abs(y), where alpha and beta are scalars, x and y are vectors and A is an n by n symmetric matrix. This function is primarily used in calculating error bounds. To protect against underflow during evaluation, components in the resulting vector are perturbed away from zero by (N+1) times the underflow threshold. To prevent unnecessarily large errors for block-structure embedded in general matrices, "symbolically" zero components are not perturbed. A zero entry is considered "symbolic" if all multiplications involved in computing that entry have at least one zero multiplicand.
real(dp) function, public	la_dla_syrcond (uplo, n, a, lda, af, ldaf, ipiv, cmode, c, info, work, iwork)
	DLA_SYRCOND: estimates the Skeel condition number of op(A) * op2(C) where op2 is determined by CMODE as follows CMODE = 1 op2(C) = C CMODE = 0 op2(C) = I CMODE = -1 op2(C) = inv(C) The Skeel condition number cond(A) = norminf( |inv(A)||A| ) is computed by computing scaling factors R such that diag(R)*A*op2(C) is row equilibrated and computing the standard infinity-norm condition number.
real(dp) function, public	la_dla_syrpvgrw (uplo, n, info, a, lda, af, ldaf, ipiv, work)
	DLA_SYRPVGRW: computes the reciprocal pivot growth factor norm(A)/norm(U). The "max absolute element" norm is used. If this is much less than 1, the stability of the LU factorization of the (equilibrated) matrix A could be poor. This also means that the solution X, estimated condition numbers, and error bounds could be unreliable.
pure subroutine, public	la_dladiv1 (a, b, c, d, p, q)
pure subroutine, public	la_dlaed6 (kniter, orgati, rho, d, z, finit, tau, info)
	DLAED6: computes the positive or negative root (closest to the origin) of z(1) z(2) z(3) f(x) = rho + ------— + -------— + ------— d(1)-x d(2)-x d(3)-x It is assumed that if ORGATI = .true. the root is between d(2) and d(3); otherwise it is between d(1) and d(2) This routine will be called by DLAED4 when necessary. In most cases, the root sought is the smallest in magnitude, though it might not be in some extremely rare situations.
pure subroutine, public	la_dlags2 (upper, a1, a2, a3, b1, b2, b3, csu, snu, csv, snv, csq, snq)
	DLAGS2: computes 2-by-2 orthogonal matrices U, V and Q, such that if ( UPPER ) then U**T A*Q = U**T *( A1 A2 )*Q = ( x 0 ) ( 0 A3 ) ( x x ) and V**T*B*Q = V**T *( B1 B2 )*Q = ( x 0 ) ( 0 B3 ) ( x x ) or if ( .NOT.UPPER ) then U**T *A*Q = U**T *( A1 0 )*Q = ( x x ) ( A2 A3 ) ( 0 x ) and V**T*B*Q = V**T( B1 0 )*Q = ( x x ) ( B2 B3 ) ( 0 x ) The rows of the transformed A and B are parallel, where U = ( CSU SNU ), V = ( CSV SNV ), Q = ( CSQ SNQ ) ( -SNU CSU ) ( -SNV CSV ) ( -SNQ CSQ ) Z**T denotes the transpose of Z.
pure subroutine, public	la_dlagtf (n, a, lambda, b, c, tol, d, in, info)
	DLAGTF: factorizes the matrix (T - lambda*I), where T is an n by n tridiagonal matrix and lambda is a scalar, as T - lambda*I = PLU, where P is a permutation matrix, L is a unit lower tridiagonal matrix with at most one non-zero sub-diagonal elements per column and U is an upper triangular matrix with at most two non-zero super-diagonal elements per column. The factorization is obtained by Gaussian elimination with partial pivoting and implicit row scaling. The parameter LAMBDA is included in the routine so that DLAGTF may be used, in conjunction with DLAGTS, to obtain eigenvectors of T by inverse iteration.
pure subroutine, public	la_dlagts (job, n, a, b, c, d, in, y, tol, info)
	DLAGTS: may be used to solve one of the systems of equations (T - lambda*I)*x = y or (T - lambda*I)**T*x = y, where T is an n by n tridiagonal matrix, for x, following the factorization of (T - lambda*I) as (T - lambda*I) = P*L*U , by routine DLAGTF. The choice of equation to be solved is controlled by the argument JOB, and in each case there is an option to perturb zero or very small diagonal elements of U, this option being intended for use in applications such as inverse iteration.
pure subroutine, public	la_dlaic1 (job, j, x, sest, w, gamma, sestpr, s, c)
	DLAIC1: applies one step of incremental condition estimation in its simplest version: Let x, twonorm(x) = 1, be an approximate singular vector of an j-by-j lower triangular matrix L, such that twonorm(L*x) = sest Then DLAIC1 computes sestpr, s, c such that the vector [ s*x ] xhat = [ c ] is an approximate singular vector of [ L 0 ] Lhat = [ w**T gamma ] in the sense that twonorm(Lhat*xhat) = sestpr. Depending on JOB, an estimate for the largest or smallest singular value is computed. Note that [s c]**T and sestpr**2 is an eigenpair of the system diag(sest*sest, 0) + [alpha gamma] * [ alpha ] [ gamma ] where alpha = x**T*w.
pure integer(ilp) function, public	la_dlaneg (n, d, lld, sigma, pivmin, r)
	DLANEG: computes the Sturm count, the number of negative pivots encountered while factoring tridiagonal T - sigma I = L D L^T. This implementation works directly on the factors without forming the tridiagonal matrix T. The Sturm count is also the number of eigenvalues of T less than sigma. This routine is called from DLARRB. The current routine does not use the PIVMIN parameter but rather requires IEEE-754 propagation of Infinities and NaNs. This routine also has no input range restrictions but does require default exception handling such that x/0 produces Inf when x is non-zero, and Inf/Inf produces NaN. For more information, see: Marques, Riedy, and Voemel, "Benefits of IEEE-754 Features in Modern Symmetric Tridiagonal Eigensolvers," SIAM Journal on Scientific Computing, v28, n5, 2006. DOI 10.1137/050641624 (Tech report version in LAWN 172 with the same title.)
real(dp) function, public	la_dlangb (norm, n, kl, ku, ab, ldab, work)
	DLANGB: returns the value of the one norm, or the Frobenius norm, or the infinity norm, or the element of largest absolute value of an n by n band matrix A, with kl sub-diagonals and ku super-diagonals.
real(dp) function, public	la_dlange (norm, m, n, a, lda, work)
	DLANGE: returns the value of the one norm, or the Frobenius norm, or the infinity norm, or the element of largest absolute value of a real matrix A.
pure real(dp) function, public	la_dlangt (norm, n, dl, d, du)
	DLANGT: returns the value of the one norm, or the Frobenius norm, or the infinity norm, or the element of largest absolute value of a real tridiagonal matrix A.
real(dp) function, public	la_dlanhs (norm, n, a, lda, work)
	DLANHS: returns the value of the one norm, or the Frobenius norm, or the infinity norm, or the element of largest absolute value of a Hessenberg matrix A.
real(dp) function, public	la_dlansb (norm, uplo, n, k, ab, ldab, work)
	DLANSB: returns the value of the one norm, or the Frobenius norm, or the infinity norm, or the element of largest absolute value of an n by n symmetric band matrix A, with k super-diagonals.
real(dp) function, public	la_dlansf (norm, transr, uplo, n, a, work)
	DLANSF: returns the value of the one norm, or the Frobenius norm, or the infinity norm, or the element of largest absolute value of a real symmetric matrix A in RFP format.
real(dp) function, public	la_dlansp (norm, uplo, n, ap, work)
	DLANSP: returns the value of the one norm, or the Frobenius norm, or the infinity norm, or the element of largest absolute value of a real symmetric matrix A, supplied in packed form.
pure real(dp) function, public	la_dlanst (norm, n, d, e)
	DLANST: returns the value of the one norm, or the Frobenius norm, or the infinity norm, or the element of largest absolute value of a real symmetric tridiagonal matrix A.
real(dp) function, public	la_dlansy (norm, uplo, n, a, lda, work)
	DLANSY: returns the value of the one norm, or the Frobenius norm, or the infinity norm, or the element of largest absolute value of a real symmetric matrix A.
real(dp) function, public	la_dlantb (norm, uplo, diag, n, k, ab, ldab, work)
	DLANTB: returns the value of the one norm, or the Frobenius norm, or the infinity norm, or the element of largest absolute value of an n by n triangular band matrix A, with ( k + 1 ) diagonals.
real(dp) function, public	la_dlantp (norm, uplo, diag, n, ap, work)
	DLANTP: returns the value of the one norm, or the Frobenius norm, or the infinity norm, or the element of largest absolute value of a triangular matrix A, supplied in packed form.
real(dp) function, public	la_dlantr (norm, uplo, diag, m, n, a, lda, work)
	DLANTR: returns the value of the one norm, or the Frobenius norm, or the infinity norm, or the element of largest absolute value of a trapezoidal or triangular matrix A.
pure subroutine, public	la_dlaorhr_col_getrfnp (m, n, a, lda, d, info)
	DLAORHR_COL_GETRFNP: computes the modified LU factorization without pivoting of a real general M-by-N matrix A. The factorization has the form: A - S = L * U, where: S is a m-by-n diagonal sign matrix with the diagonal D, so that D(i) = S(i,i), 1 <= i <= min(M,N). The diagonal D is constructed as D(i)=-SIGN(A(i,i)), where A(i,i) is the value after performing i-1 steps of Gaussian elimination. This means that the diagonal element at each step of "modified" Gaussian elimination is at least one in absolute value (so that division-by-zero not not possible during the division by the diagonal element); L is a M-by-N lower triangular matrix with unit diagonal elements (lower trapezoidal if M > N); and U is a M-by-N upper triangular matrix (upper trapezoidal if M < N). This routine is an auxiliary routine used in the Householder reconstruction routine DORHR_COL. In DORHR_COL, this routine is applied to an M-by-N matrix A with orthonormal columns, where each element is bounded by one in absolute value. With the choice of the matrix S above, one can show that the diagonal element at each step of Gaussian elimination is the largest (in absolute value) in the column on or below the diagonal, so that no pivoting is required for numerical stability [1]. For more details on the Householder reconstruction algorithm, including the modified LU factorization, see [1]. This is the blocked right-looking version of the algorithm, calling Level 3 BLAS to update the submatrix. To factorize a block, this routine calls the recursive routine DLAORHR_COL_GETRFNP2. [1] "Reconstructing Householder vectors from tall-skinny QR", G. Ballard, J. Demmel, L. Grigori, M. Jacquelin, H.D. Nguyen, E. Solomonik, J. Parallel Distrib. Comput., vol. 85, pp. 3-31, 2015.
pure real(dp) function, public	la_dlapy2 (x, y)
	DLAPY2: returns sqrt(x**2+y**2), taking care not to cause unnecessary overflow and unnecessary underflow.
pure subroutine, public	la_dlaqz1 (a, lda, b, ldb, sr1, sr2, si, beta1, beta2, v)
	Given a 3-by-3 matrix pencil (A,B), DLAQZ1: sets v to a scalar multiple of the first column of the product (*) K = (A - (beta2*sr2 - i*si)*B)*B^(-1)*(beta1*A - (sr2 + i*si2)*B)*B^(-1). It is assumed that either 1) sr1 = sr2 or 2) si = 0. This is useful for starting double implicit shift bulges in the QZ algorithm.
pure subroutine, public	la_dlaqz2 (ilq, ilz, k, istartm, istopm, ihi, a, lda, b, ldb, nq, qstart, q, ldq, nz, zstart, z, ldz)
	DLAQZ2: chases a 2x2 shift bulge in a matrix pencil down a single position.
pure subroutine, public	la_dlaqz4 (ilschur, ilq, ilz, n, ilo, ihi, nshifts, nblock_desired, sr, si, ss, a, lda, b, ldb, q, ldq, z, ldz, qc, ldqc, zc, ldzc, work, lwork, info)
	DLAQZ4: Executes a single multishift QZ sweep.
pure subroutine, public	la_dlar1v (n, b1, bn, lambda, d, l, ld, lld, pivmin, gaptol, z, wantnc, negcnt, ztz, mingma, r, isuppz, nrminv, resid, rqcorr, work)
	DLAR1V: computes the (scaled) r-th column of the inverse of the sumbmatrix in rows B1 through BN of the tridiagonal matrix L D L**T - sigma I. When sigma is close to an eigenvalue, the computed vector is an accurate eigenvector. Usually, r corresponds to the index where the eigenvector is largest in magnitude. The following steps accomplish this computation : (a) Stationary qd transform, L D L**T - sigma I = L(+) D(+) L(+)**T, (b) Progressive qd transform, L D L**T - sigma I = U(-) D(-) U(-)**T, (c) Computation of the diagonal elements of the inverse of L D L**T - sigma I by combining the above transforms, and choosing r as the index where the diagonal of the inverse is (one of the) largest in magnitude. (d) Computation of the (scaled) r-th column of the inverse using the twisted factorization obtained by combining the top part of the the stationary and the bottom part of the progressive transform.
pure subroutine, public	la_dlarfg (n, alpha, x, incx, tau)
	DLARFG: generates a real elementary reflector H of order n, such that H * ( alpha ) = ( beta ), H**T * H = I. ( x ) ( 0 ) where alpha and beta are scalars, and x is an (n-1)-element real vector. H is represented in the form H = I - tau * ( 1 ) * ( 1 v**T ) , ( v ) where tau is a real scalar and v is a real (n-1)-element vector. If the elements of x are all zero, then tau = 0 and H is taken to be the unit matrix. Otherwise 1 <= tau <= 2.
subroutine, public	la_dlarfgp (n, alpha, x, incx, tau)
	DLARFGP: generates a real elementary reflector H of order n, such that H * ( alpha ) = ( beta ), H**T * H = I. ( x ) ( 0 ) where alpha and beta are scalars, beta is non-negative, and x is an (n-1)-element real vector. H is represented in the form H = I - tau * ( 1 ) * ( 1 v**T ) , ( v ) where tau is a real scalar and v is a real (n-1)-element vector. If the elements of x are all zero, then tau = 0 and H is taken to be the unit matrix.
pure subroutine, public	la_dlarnv (idist, iseed, n, x)
	DLARNV: returns a vector of n random real numbers from a uniform or normal distribution.
pure subroutine, public	la_dlarrb (n, d, lld, ifirst, ilast, rtol1, rtol2, offset, w, wgap, werr, work, iwork, pivmin, spdiam, twist, info)
	Given the relatively robust representation(RRR) L D L^T, DLARRB: does "limited" bisection to refine the eigenvalues of L D L^T, W( IFIRST-OFFSET ) through W( ILAST-OFFSET ), to more accuracy. Initial guesses for these eigenvalues are input in W, the corresponding estimate of the error in these guesses and their gaps are input in WERR and WGAP, respectively. During bisection, intervals [left, right] are maintained by storing their mid-points and semi-widths in the arrays W and WERR respectively.
pure subroutine, public	la_dlarrf (n, d, l, ld, clstrt, clend, w, wgap, werr, spdiam, clgapl, clgapr, pivmin, sigma, dplus, lplus, work, info)
	Given the initial representation L D L^T and its cluster of close eigenvalues (in a relative measure), W( CLSTRT ), W( CLSTRT+1 ), ... W( CLEND ), DLARRF: finds a new relatively robust representation L D L^T - SIGMA I = L(+) D(+) L(+)^T such that at least one of the eigenvalues of L(+) D(+) L(+)^T is relatively isolated.
pure subroutine, public	la_dlarrv (n, vl, vu, d, l, pivmin, isplit, m, dol, dou, minrgp, rtol1, rtol2, w, werr, wgap, iblock, indexw, gers, z, ldz, isuppz, work, iwork, info)
	DLARRV: computes the eigenvectors of the tridiagonal matrix T = L D L**T given L, D and APPROXIMATIONS to the eigenvalues of L D L**T. The input eigenvalues should have been computed by DLARRE.
pure subroutine, public	la_dlascl (type, kl, ku, cfrom, cto, m, n, a, lda, info)
	DLASCL: multiplies the M by N real matrix A by the real scalar CTO/CFROM. This is done without over/underflow as long as the final result CTO*A(I,J)/CFROM does not over/underflow. TYPE specifies that A may be full, upper triangular, lower triangular, upper Hessenberg, or banded.
pure subroutine, public	la_dlasd4 (n, i, d, z, delta, rho, sigma, work, info)
	This subroutine computes the square root of the I-th updated eigenvalue of a positive symmetric rank-one modification to a positive diagonal matrix whose entries are given as the squares of the corresponding entries in the array d, and that 0 <= D(i) < D(j) for i < j and that RHO > 0. This is arranged by the calling routine, and is no loss in generality. The rank-one modified system is thus diag( D ) * diag( D ) + RHO * Z * Z_transpose. where we assume the Euclidean norm of Z is 1. The method consists of approximating the rational functions in the secular equation by simpler interpolating rational functions.
pure subroutine, public	la_dlasd7 (icompq, nl, nr, sqre, k, d, z, zw, vf, vfw, vl, vlw, alpha, beta, dsigma, idx, idxp, idxq, perm, givptr, givcol, ldgcol, givnum, ldgnum, c, s, info)
	DLASD7: merges the two sets of singular values together into a single sorted set. Then it tries to deflate the size of the problem. There are two ways in which deflation can occur: when two or more singular values are close together or if there is a tiny entry in the Z vector. For each such occurrence the order of the related secular equation problem is reduced by one. DLASD7 is called from DLASD6.
pure subroutine, public	la_dlasd8 (icompq, k, d, z, vf, vl, difl, difr, lddifr, dsigma, work, info)
	DLASD8: finds the square roots of the roots of the secular equation, as defined by the values in DSIGMA and Z. It makes the appropriate calls to DLASD4, and stores, for each element in D, the distance to its two nearest poles (elements in DSIGMA). It also updates the arrays VF and VL, the first and last components of all the right singular vectors of the original bidiagonal matrix. DLASD8 is called from DLASD6.
pure subroutine, public	la_dlasq3 (i0, n0, z, pp, dmin, sigma, desig, qmax, nfail, iter, ndiv, ieee, ttype, dmin1, dmin2, dn, dn1, dn2, g, tau)
	DLASQ3: checks for deflation, computes a shift (TAU) and calls dqds. In case of failure it changes shifts, and tries again until output is positive.
pure subroutine, public	la_dlatdf (ijob, n, z, ldz, rhs, rdsum, rdscal, ipiv, jpiv)
	DLATDF: uses the LU factorization of the n-by-n matrix Z computed by DGETC2 and computes a contribution to the reciprocal Dif-estimate by solving Z * x = b for x, and choosing the r.h.s. b such that the norm of x is as large as possible. On entry RHS = b holds the contribution from earlier solved sub-systems, and on return RHS = x. The factorization of Z returned by DGETC2 has the form Z = P*L*U*Q, where P and Q are permutation matrices. L is lower triangular with unit diagonal elements and U is upper triangular.
pure subroutine, public	la_dlatrd (uplo, n, nb, a, lda, e, tau, w, ldw)
	DLATRD: reduces NB rows and columns of a real symmetric matrix A to symmetric tridiagonal form by an orthogonal similarity transformation Q**T * A * Q, and returns the matrices V and W which are needed to apply the transformation to the unreduced part of A. If UPLO = 'U', DLATRD reduces the last NB rows and columns of a matrix, of which the upper triangle is supplied; if UPLO = 'L', DLATRD reduces the first NB rows and columns of a matrix, of which the lower triangle is supplied. This is an auxiliary routine called by DSYTRD.
pure subroutine, public	la_dlatrz (m, n, l, a, lda, tau, work)
	DLATRZ: factors the M-by-(M+L) real upper trapezoidal matrix [ A1 A2 ] = [ A(1:M,1:M) A(1:M,N-L+1:N) ] as ( R 0 ) * Z, by means of orthogonal transformations. Z is an (M+L)-by-(M+L) orthogonal matrix and, R and A1 are M-by-M upper triangular matrices.
subroutine, public	la_dorbdb (trans, signs, m, p, q, x11, ldx11, x12, ldx12, x21, ldx21, x22, ldx22, theta, phi, taup1, taup2, tauq1, tauq2, work, lwork, info)
	DORBDB: simultaneously bidiagonalizes the blocks of an M-by-M partitioned orthogonal matrix X: [ B11 | B12 0 0 ] [ X11 | X12 ] [ P1 | ] [ 0 | 0 -I 0 ] [ Q1 | ]**T X = [--------—] = [------—] [-------------—] [------—] . [ X21 | X22 ] [ | P2 ] [ B21 | B22 0 0 ] [ | Q2 ] [ 0 | 0 0 I ] X11 is P-by-Q. Q must be no larger than P, M-P, or M-Q. (If this is not the case, then X must be transposed and/or permuted. This can be done in constant time using the TRANS and SIGNS options. See DORCSD for details.) The orthogonal matrices P1, P2, Q1, and Q2 are P-by-P, (M-P)-by- (M-P), Q-by-Q, and (M-Q)-by-(M-Q), respectively. They are represented implicitly by Householder vectors. B11, B12, B21, and B22 are Q-by-Q bidiagonal matrices represented implicitly by angles THETA, PHI.
pure subroutine, public	la_dorbdb5 (m1, m2, n, x1, incx1, x2, incx2, q1, ldq1, q2, ldq2, work, lwork, info)
	DORBDB5: orthogonalizes the column vector X = [ X1 ] [ X2 ] with respect to the columns of Q = [ Q1 ] . [ Q2 ] The columns of Q must be orthonormal. If the projection is zero according to Kahan's "twice is enough" criterion, then some other vector from the orthogonal complement is returned. This vector is chosen in an arbitrary but deterministic way.
recursive subroutine, public	la_dorcsd (jobu1, jobu2, jobv1t, jobv2t, trans, signs, m, p, q, x11, ldx11, x12, ldx12, x21, ldx21, x22, ldx22, theta, u1, ldu1, u2, ldu2, v1t, ldv1t, v2t, ldv2t, work, lwork, iwork, info)
	DORCSD: computes the CS decomposition of an M-by-M partitioned orthogonal matrix X: [ I 0 0 | 0 0 0 ] [ 0 C 0 | 0 -S 0 ] [ X11 | X12 ] [ U1 | ] [ 0 0 0 | 0 0 -I ] [ V1 | ]**T X = [--------—] = [------—] [------------------—] [------—] . [ X21 | X22 ] [ | U2 ] [ 0 0 0 | I 0 0 ] [ | V2 ] [ 0 S 0 | 0 C 0 ] [ 0 0 I | 0 0 0 ] X11 is P-by-Q. The orthogonal matrices U1, U2, V1, and V2 are P-by-P, (M-P)-by-(M-P), Q-by-Q, and (M-Q)-by-(M-Q), respectively. C and S are R-by-R nonnegative diagonal matrices satisfying C^2 + S^2 = I, in which R = MIN(P,M-P,Q,M-Q).
pure subroutine, public	la_dorghr (n, ilo, ihi, a, lda, tau, work, lwork, info)
	DORGHR: generates a real orthogonal matrix Q which is defined as the product of IHI-ILO elementary reflectors of order N, as returned by DGEHRD: Q = H(ilo) H(ilo+1) . . . H(ihi-1).
pure subroutine, public	la_dorhr_col (m, n, nb, a, lda, t, ldt, d, info)
	DORHR_COL: takes an M-by-N real matrix Q_in with orthonormal columns as input, stored in A, and performs Householder Reconstruction (HR), i.e. reconstructs Householder vectors V(i) implicitly representing another M-by-N matrix Q_out, with the property that Q_in = Q_out*S, where S is an N-by-N diagonal matrix with diagonal entries equal to +1 or -1. The Householder vectors (columns V(i) of V) are stored in A on output, and the diagonal entries of S are stored in D. Block reflectors are also returned in T (same output format as DGEQRT).
pure subroutine, public	la_dormhr (side, trans, m, n, ilo, ihi, a, lda, tau, c, ldc, work, lwork, info)
	DORMHR: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q * C C * Q TRANS = 'T': Q**T * C C * Q**T where Q is a real orthogonal matrix of order nq, with nq = m if SIDE = 'L' and nq = n if SIDE = 'R'. Q is defined as the product of IHI-ILO elementary reflectors, as returned by DGEHRD: Q = H(ilo) H(ilo+1) . . . H(ihi-1).
pure subroutine, public	la_dpbcon (uplo, n, kd, ab, ldab, anorm, rcond, work, iwork, info)
	DPBCON: estimates the reciprocal of the condition number (in the 1-norm) of a real symmetric positive definite band matrix using the Cholesky factorization A = U**T*U or A = L*L**T computed by DPBTRF. An estimate is obtained for norm(inv(A)), and the reciprocal of the condition number is computed as RCOND = 1 / (ANORM * norm(inv(A))).
pure subroutine, public	la_dpbrfs (uplo, n, kd, nrhs, ab, ldab, afb, ldafb, b, ldb, x, ldx, ferr, berr, work, iwork, info)
	DPBRFS: improves the computed solution to a system of linear equations when the coefficient matrix is symmetric positive definite and banded, and provides error bounds and backward error estimates for the solution.
pure subroutine, public	la_dpftrs (transr, uplo, n, nrhs, a, b, ldb, info)
	DPFTRS: solves a system of linear equations A*X = B with a symmetric positive definite matrix A using the Cholesky factorization A = U**T*U or A = L*L**T computed by DPFTRF.
pure subroutine, public	la_dpocon (uplo, n, a, lda, anorm, rcond, work, iwork, info)
	DPOCON: estimates the reciprocal of the condition number (in the 1-norm) of a real symmetric positive definite matrix using the Cholesky factorization A = U**T*U or A = L*L**T computed by DPOTRF. An estimate is obtained for norm(inv(A)), and the reciprocal of the condition number is computed as RCOND = 1 / (ANORM * norm(inv(A))).
pure subroutine, public	la_dporfs (uplo, n, nrhs, a, lda, af, ldaf, b, ldb, x, ldx, ferr, berr, work, iwork, info)
	DPORFS: improves the computed solution to a system of linear equations when the coefficient matrix is symmetric positive definite, and provides error bounds and backward error estimates for the solution.
pure subroutine, public	la_dpotf2 (uplo, n, a, lda, info)
	DPOTF2: computes the Cholesky factorization of a real symmetric positive definite matrix A. The factorization has the form A = U**T * U , if UPLO = 'U', or A = L * L**T, if UPLO = 'L', where U is an upper triangular matrix and L is lower triangular. This is the unblocked version of the algorithm, calling Level 2 BLAS.
pure recursive subroutine, public	la_dpotrf2 (uplo, n, a, lda, info)
	DPOTRF2: computes the Cholesky factorization of a real symmetric positive definite matrix A using the recursive algorithm. The factorization has the form A = U**T * U, if UPLO = 'U', or A = L * L**T, if UPLO = 'L', where U is an upper triangular matrix and L is lower triangular. This is the recursive version of the algorithm. It divides the matrix into four submatrices: [ A11 | A12 ] where A11 is n1 by n1 and A22 is n2 by n2 A = [ --—|--— ] with n1 = n/2 [ A21 | A22 ] n2 = n-n1 The subroutine calls itself to factor A11. Update and scale A21 or A12, update A22 then calls itself to factor A22.
pure subroutine, public	la_dpotri (uplo, n, a, lda, info)
	DPOTRI: computes the inverse of a real symmetric positive definite matrix A using the Cholesky factorization A = U**T*U or A = L*L**T computed by DPOTRF.
pure subroutine, public	la_dppcon (uplo, n, ap, anorm, rcond, work, iwork, info)
	DPPCON: estimates the reciprocal of the condition number (in the 1-norm) of a real symmetric positive definite packed matrix using the Cholesky factorization A = U**T*U or A = L*L**T computed by DPPTRF. An estimate is obtained for norm(inv(A)), and the reciprocal of the condition number is computed as RCOND = 1 / (ANORM * norm(inv(A))).
pure subroutine, public	la_dpprfs (uplo, n, nrhs, ap, afp, b, ldb, x, ldx, ferr, berr, work, iwork, info)
	DPPRFS: improves the computed solution to a system of linear equations when the coefficient matrix is symmetric positive definite and packed, and provides error bounds and backward error estimates for the solution.
pure subroutine, public	la_dppsv (uplo, n, nrhs, ap, b, ldb, info)
	DPPSV: computes the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric positive definite matrix stored in packed format and X and B are N-by-NRHS matrices. The Cholesky decomposition is used to factor A as A = U**T* U, if UPLO = 'U', or A = L * L**T, if UPLO = 'L', where U is an upper triangular matrix and L is a lower triangular matrix. The factored form of A is then used to solve the system of equations A * X = B.
subroutine, public	la_dppsvx (fact, uplo, n, nrhs, ap, afp, equed, s, b, ldb, x, ldx, rcond, ferr, berr, work, iwork, info)
	DPPSVX: uses the Cholesky factorization A = U**T*U or A = L*L**T to compute the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric positive definite matrix stored in packed format and X and B are N-by-NRHS matrices. Error bounds on the solution and a condition estimate are also provided.
pure subroutine, public	la_dpptri (uplo, n, ap, info)
	DPPTRI: computes the inverse of a real symmetric positive definite matrix A using the Cholesky factorization A = U**T*U or A = L*L**T computed by DPPTRF.
pure subroutine, public	la_dpstf2 (uplo, n, a, lda, piv, rank, tol, work, info)
	DPSTF2: computes the Cholesky factorization with complete pivoting of a real symmetric positive semidefinite matrix A. The factorization has the form P**T * A * P = U**T * U , if UPLO = 'U', P**T * A * P = L * L**T, if UPLO = 'L', where U is an upper triangular matrix and L is lower triangular, and P is stored as vector PIV. This algorithm does not attempt to check that A is positive semidefinite. This version of the algorithm calls level 2 BLAS.
pure subroutine, public	la_dpstrf (uplo, n, a, lda, piv, rank, tol, work, info)
	DPSTRF: computes the Cholesky factorization with complete pivoting of a real symmetric positive semidefinite matrix A. The factorization has the form P**T * A * P = U**T * U , if UPLO = 'U', P**T * A * P = L * L**T, if UPLO = 'L', where U is an upper triangular matrix and L is lower triangular, and P is stored as vector PIV. This algorithm does not attempt to check that A is positive semidefinite. This version of the algorithm calls level 3 BLAS.
pure subroutine, public	la_dpttrs (n, nrhs, d, e, b, ldb, info)
	DPTTRS: solves a tridiagonal system of the form A * X = B using the L*D*L**T factorization of A computed by DPTTRF. D is a diagonal matrix specified in the vector D, L is a unit bidiagonal matrix whose subdiagonal is specified in the vector E, and X and B are N by NRHS matrices.
pure subroutine, public	la_dsb2st_kernels (uplo, wantz, ttype, st, ed, sweep, n, nb, ib, a, lda, v, tau, ldvt, work)
	DSB2ST_KERNELS: is an internal routine used by the DSYTRD_SB2ST subroutine.
pure subroutine, public	la_dspcon (uplo, n, ap, ipiv, anorm, rcond, work, iwork, info)
	DSPCON: estimates the reciprocal of the condition number (in the 1-norm) of a real symmetric packed matrix A using the factorization A = U*D*U**T or A = L*D*L**T computed by DSPTRF. An estimate is obtained for norm(inv(A)), and the reciprocal of the condition number is computed as RCOND = 1 / (ANORM * norm(inv(A))).
pure subroutine, public	la_dsprfs (uplo, n, nrhs, ap, afp, ipiv, b, ldb, x, ldx, ferr, berr, work, iwork, info)
	DSPRFS: improves the computed solution to a system of linear equations when the coefficient matrix is symmetric indefinite and packed, and provides error bounds and backward error estimates for the solution.
pure subroutine, public	la_dspsv (uplo, n, nrhs, ap, ipiv, b, ldb, info)
	DSPSV: computes the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric matrix stored in packed format and X and B are N-by-NRHS matrices. The diagonal pivoting method is used to factor A as A = U * D * U**T, if UPLO = 'U', or A = L * D * L**T, if UPLO = 'L', where U (or L) is a product of permutation and unit upper (lower) triangular matrices, D is symmetric and block diagonal with 1-by-1 and 2-by-2 diagonal blocks. The factored form of A is then used to solve the system of equations A * X = B.
subroutine, public	la_dspsvx (fact, uplo, n, nrhs, ap, afp, ipiv, b, ldb, x, ldx, rcond, ferr, berr, work, iwork, info)
	DSPSVX: uses the diagonal pivoting factorization A = U*D*U**T or A = L*D*L**T to compute the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric matrix stored in packed format and X and B are N-by-NRHS matrices. Error bounds on the solution and a condition estimate are also provided.
pure subroutine, public	la_dsptrd (uplo, n, ap, d, e, tau, info)
	DSPTRD: reduces a real symmetric matrix A stored in packed form to symmetric tridiagonal form T by an orthogonal similarity transformation: Q**T * A * Q = T.
pure subroutine, public	la_dstein (n, d, e, m, w, iblock, isplit, z, ldz, work, iwork, ifail, info)
	DSTEIN: computes the eigenvectors of a real symmetric tridiagonal matrix T corresponding to specified eigenvalues, using inverse iteration. The maximum number of iterations allowed for each eigenvector is specified by an internal parameter MAXITS (currently set to 5).
pure subroutine, public	la_dsteqr (compz, n, d, e, z, ldz, work, info)
	DSTEQR: computes all eigenvalues and, optionally, eigenvectors of a symmetric tridiagonal matrix using the implicit QL or QR method. The eigenvectors of a full or band symmetric matrix can also be found if DSYTRD or DSPTRD or DSBTRD has been used to reduce this matrix to tridiagonal form.
pure subroutine, public	la_dsterf (n, d, e, info)
	DSTERF: computes all eigenvalues of a symmetric tridiagonal matrix using the Pal-Walker-Kahan variant of the QL or QR algorithm.
pure subroutine, public	la_dstev (jobz, n, d, e, z, ldz, work, info)
	DSTEV: computes all eigenvalues and, optionally, eigenvectors of a real symmetric tridiagonal matrix A.
pure subroutine, public	la_dstevx (jobz, range, n, d, e, vl, vu, il, iu, abstol, m, w, z, ldz, work, iwork, ifail, info)
	DSTEVX: computes selected eigenvalues and, optionally, eigenvectors of a real symmetric tridiagonal matrix A. Eigenvalues and eigenvectors can be selected by specifying either a range of values or a range of indices for the desired eigenvalues.
pure subroutine, public	la_dsycon (uplo, n, a, lda, ipiv, anorm, rcond, work, iwork, info)
	DSYCON: estimates the reciprocal of the condition number (in the 1-norm) of a real symmetric matrix A using the factorization A = U*D*U**T or A = L*D*L**T computed by DSYTRF. An estimate is obtained for norm(inv(A)), and the reciprocal of the condition number is computed as RCOND = 1 / (ANORM * norm(inv(A))).
pure subroutine, public	la_dsycon_rook (uplo, n, a, lda, ipiv, anorm, rcond, work, iwork, info)
	DSYCON_ROOK: estimates the reciprocal of the condition number (in the 1-norm) of a real symmetric matrix A using the factorization A = U*D*U**T or A = L*D*L**T computed by DSYTRF_ROOK. An estimate is obtained for norm(inv(A)), and the reciprocal of the condition number is computed as RCOND = 1 / (ANORM * norm(inv(A))).
pure subroutine, public	la_dsyrfs (uplo, n, nrhs, a, lda, af, ldaf, ipiv, b, ldb, x, ldx, ferr, berr, work, iwork, info)
	DSYRFS: improves the computed solution to a system of linear equations when the coefficient matrix is symmetric indefinite, and provides error bounds and backward error estimates for the solution.
pure subroutine, public	la_dsysv_rk (uplo, n, nrhs, a, lda, e, ipiv, b, ldb, work, lwork, info)
	DSYSV_RK: computes the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric matrix and X and B are N-by-NRHS matrices. The bounded Bunch-Kaufman (rook) diagonal pivoting method is used to factor A as A = P*U*D*(U**T)*(P**T), if UPLO = 'U', or A = P*L*D*(L**T)*(P**T), if UPLO = 'L', where U (or L) is unit upper (or lower) triangular matrix, U**T (or L**T) is the transpose of U (or L), P is a permutation matrix, P**T is the transpose of P, and D is symmetric and block diagonal with 1-by-1 and 2-by-2 diagonal blocks. DSYTRF_RK is called to compute the factorization of a real symmetric matrix. The factored form of A is then used to solve the system of equations A * X = B by calling BLAS3 routine DSYTRS_3.
pure subroutine, public	la_dsysv_rook (uplo, n, nrhs, a, lda, ipiv, b, ldb, work, lwork, info)
	DSYSV_ROOK: computes the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric matrix and X and B are N-by-NRHS matrices. The diagonal pivoting method is used to factor A as A = U * D * U**T, if UPLO = 'U', or A = L * D * L**T, if UPLO = 'L', where U (or L) is a product of permutation and unit upper (lower) triangular matrices, and D is symmetric and block diagonal with 1-by-1 and 2-by-2 diagonal blocks. DSYTRF_ROOK is called to compute the factorization of a real symmetric matrix A using the bounded Bunch-Kaufman ("rook") diagonal pivoting method. The factored form of A is then used to solve the system of equations A * X = B by calling DSYTRS_ROOK.
pure subroutine, public	la_dsytd2 (uplo, n, a, lda, d, e, tau, info)
	DSYTD2: reduces a real symmetric matrix A to symmetric tridiagonal form T by an orthogonal similarity transformation: Q**T * A * Q = T.
pure subroutine, public	la_dsytf2 (uplo, n, a, lda, ipiv, info)
	DSYTF2: computes the factorization of a real symmetric matrix A using the Bunch-Kaufman diagonal pivoting method: A = U*D*U**T or A = L*D*L**T where U (or L) is a product of permutation and unit upper (lower) triangular matrices, U**T is the transpose of U, and D is symmetric and block diagonal with 1-by-1 and 2-by-2 diagonal blocks. This is the unblocked version of the algorithm, calling Level 2 BLAS.
pure subroutine, public	la_dsytrd (uplo, n, a, lda, d, e, tau, work, lwork, info)
	DSYTRD: reduces a real symmetric matrix A to real symmetric tridiagonal form T by an orthogonal similarity transformation: Q**T * A * Q = T.
pure subroutine, public	la_dsytrd_sb2st (stage1, vect, uplo, n, kd, ab, ldab, d, e, hous, lhous, work, lwork, info)
	DSYTRD_SB2ST: reduces a real symmetric band matrix A to real symmetric tridiagonal form T by a orthogonal similarity transformation: Q**T * A * Q = T.
pure subroutine, public	la_dsytrf (uplo, n, a, lda, ipiv, work, lwork, info)
	DSYTRF: computes the factorization of a real symmetric matrix A using the Bunch-Kaufman diagonal pivoting method. The form of the factorization is A = U**T*D*U or A = L*D*L**T where U (or L) is a product of permutation and unit upper (lower) triangular matrices, and D is symmetric and block diagonal with 1-by-1 and 2-by-2 diagonal blocks. This is the blocked version of the algorithm, calling Level 3 BLAS.
subroutine, public	la_dtbcon (norm, uplo, diag, n, kd, ab, ldab, rcond, work, iwork, info)
	DTBCON: estimates the reciprocal of the condition number of a triangular band matrix A, in either the 1-norm or the infinity-norm. The norm of A is computed and an estimate is obtained for norm(inv(A)), then the reciprocal of the condition number is computed as RCOND = 1 / ( norm(A) * norm(inv(A)) ).
pure subroutine, public	la_dtftri (transr, uplo, diag, n, a, info)
	DTFTRI: computes the inverse of a triangular matrix A stored in RFP format. This is a Level 3 BLAS version of the algorithm.
pure subroutine, public	la_dtgsy2 (trans, ijob, m, n, a, lda, b, ldb, c, ldc, d, ldd, e, lde, f, ldf, scale, rdsum, rdscal, iwork, pq, info)
	DTGSY2: solves the generalized Sylvester equation: A * R - L * B = scale * C (1) D * R - L * E = scale * F, using Level 1 and 2 BLAS. where R and L are unknown M-by-N matrices, (A, D), (B, E) and (C, F) are given matrix pairs of size M-by-M, N-by-N and M-by-N, respectively, with real entries. (A, D) and (B, E) must be in generalized Schur canonical form, i.e. A, B are upper quasi triangular and D, E are upper triangular. The solution (R, L) overwrites (C, F). 0 <= SCALE <= 1 is an output scaling factor chosen to avoid overflow. In matrix notation solving equation (1) corresponds to solve Z*x = scale*b, where Z is defined as Z = [ kron(In, A) -kron(B**T, Im) ] (2) [ kron(In, D) -kron(E**T, Im) ], Ik is the identity matrix of size k and X**T is the transpose of X. kron(X, Y) is the Kronecker product between the matrices X and Y. In the process of solving (1), we solve a number of such systems where Dim(In), Dim(In) = 1 or 2. If TRANS = 'T', solve the transposed system Z**T*y = scale*b for y, which is equivalent to solve for R and L in A**T * R + D**T * L = scale * C (3) R * B**T + L * E**T = scale * -F This case is used to compute an estimate of Dif[(A, D), (B, E)] = sigma_min(Z) using reverse communication with DLACON. DTGSY2 also (IJOB >= 1) contributes to the computation in DTGSYL of an upper bound on the separation between to matrix pairs. Then the input (A, D), (B, E) are sub-pencils of the matrix pair in DTGSYL. See DTGSYL for details.
pure subroutine, public	la_dtgsyl (trans, ijob, m, n, a, lda, b, ldb, c, ldc, d, ldd, e, lde, f, ldf, scale, dif, work, lwork, iwork, info)
	DTGSYL: solves the generalized Sylvester equation: A * R - L * B = scale * C (1) D * R - L * E = scale * F where R and L are unknown m-by-n matrices, (A, D), (B, E) and (C, F) are given matrix pairs of size m-by-m, n-by-n and m-by-n, respectively, with real entries. (A, D) and (B, E) must be in generalized (real) Schur canonical form, i.e. A, B are upper quasi triangular and D, E are upper triangular. The solution (R, L) overwrites (C, F). 0 <= SCALE <= 1 is an output scaling factor chosen to avoid overflow. In matrix notation (1) is equivalent to solve Zx = scale b, where Z is defined as Z = [ kron(In, A) -kron(B**T, Im) ] (2) [ kron(In, D) -kron(E**T, Im) ]. Here Ik is the identity matrix of size k and X**T is the transpose of X. kron(X, Y) is the Kronecker product between the matrices X and Y. If TRANS = 'T', DTGSYL solves the transposed system Z**T*y = scale*b, which is equivalent to solve for R and L in A**T * R + D**T * L = scale * C (3) R * B**T + L * E**T = scale * -F This case (TRANS = 'T') is used to compute an one-norm-based estimate of Dif[(A,D), (B,E)], the separation between the matrix pairs (A,D) and (B,E), using DLACON. If IJOB >= 1, DTGSYL computes a Frobenius norm-based estimate of Dif[(A,D),(B,E)]. That is, the reciprocal of a lower bound on the reciprocal of the smallest singular value of Z. See [1-2] for more information. This is a level 3 BLAS algorithm.
subroutine, public	la_dtpcon (norm, uplo, diag, n, ap, rcond, work, iwork, info)
	DTPCON: estimates the reciprocal of the condition number of a packed triangular matrix A, in either the 1-norm or the infinity-norm. The norm of A is computed and an estimate is obtained for norm(inv(A)), then the reciprocal of the condition number is computed as RCOND = 1 / ( norm(A) * norm(inv(A)) ).
pure subroutine, public	la_dtplqt2 (m, n, l, a, lda, b, ldb, t, ldt, info)
	DTPLQT2: computes a LQ a factorization of a real "triangular-pentagonal" matrix C, which is composed of a triangular block A and pentagonal block B, using the compact WY representation for Q.
pure subroutine, public	la_dtpmlqt (side, trans, m, n, k, l, mb, v, ldv, t, ldt, a, lda, b, ldb, work, info)
	DTPMQRT applies a real orthogonal matrix Q obtained from a "triangular-pentagonal" real block reflector H to a general real matrix C, which consists of two blocks A and B.
pure subroutine, public	la_dtpmqrt (side, trans, m, n, k, l, nb, v, ldv, t, ldt, a, lda, b, ldb, work, info)
	DTPMQRT: applies a real orthogonal matrix Q obtained from a "triangular-pentagonal" real block reflector H to a general real matrix C, which consists of two blocks A and B.
pure subroutine, public	la_dtpqrt2 (m, n, l, a, lda, b, ldb, t, ldt, info)
	DTPQRT2: computes a QR factorization of a real "triangular-pentagonal" matrix C, which is composed of a triangular block A and pentagonal block B, using the compact WY representation for Q.
subroutine, public	la_dtrcon (norm, uplo, diag, n, a, lda, rcond, work, iwork, info)
	DTRCON: estimates the reciprocal of the condition number of a triangular matrix A, in either the 1-norm or the infinity-norm. The norm of A is computed and an estimate is obtained for norm(inv(A)), then the reciprocal of the condition number is computed as RCOND = 1 / ( norm(A) * norm(inv(A)) ).
pure subroutine, public	la_dtzrzf (m, n, a, lda, tau, work, lwork, info)
	DTZRZF: reduces the M-by-N ( M<=N ) real upper trapezoidal matrix A to upper triangular form by means of orthogonal transformations. The upper trapezoidal matrix A is factored as A = ( R 0 ) * Z, where Z is an N-by-N orthogonal matrix and R is an M-by-M upper triangular matrix.
pure subroutine, public	la_dgbsv (n, kl, ku, nrhs, ab, ldab, ipiv, b, ldb, info)
	DGBSV: computes the solution to a real system of linear equations A * X = B, where A is a band matrix of order N with KL subdiagonals and KU superdiagonals, and X and B are N-by-NRHS matrices. The LU decomposition with partial pivoting and row interchanges is used to factor A as A = L * U, where L is a product of permutation and unit lower triangular matrices with KL subdiagonals, and U is upper triangular with KL+KU superdiagonals. The factored form of A is then used to solve the system of equations A * X = B.
subroutine, public	la_dgbsvx (fact, trans, n, kl, ku, nrhs, ab, ldab, afb, ldafb, ipiv, equed, r, c, b, ldb, x, ldx, rcond, ferr, berr, work, iwork, info)
	DGBSVX: uses the LU factorization to compute the solution to a real system of linear equations A * X = B, A**T * X = B, or A**H * X = B, where A is a band matrix of order N with KL subdiagonals and KU superdiagonals, and X and B are N-by-NRHS matrices. Error bounds on the solution and a condition estimate are also provided.
pure subroutine, public	la_dgebal (job, n, a, lda, ilo, ihi, scale, info)
	DGEBAL: balances a general real matrix A. This involves, first, permuting A by a similarity transformation to isolate eigenvalues in the first 1 to ILO-1 and last IHI+1 to N elements on the diagonal; and second, applying a diagonal similarity transformation to rows and columns ILO to IHI to make the rows and columns as close in norm as possible. Both steps are optional. Balancing may reduce the 1-norm of the matrix, and improve the accuracy of the computed eigenvalues and/or eigenvectors.
pure subroutine, public	la_dgebd2 (m, n, a, lda, d, e, tauq, taup, work, info)
	DGEBD2: reduces a real general m by n matrix A to upper or lower bidiagonal form B by an orthogonal transformation: Q**T * A * P = B. If m >= n, B is upper bidiagonal; if m < n, B is lower bidiagonal.
pure subroutine, public	la_dgehd2 (n, ilo, ihi, a, lda, tau, work, info)
	DGEHD2: reduces a real general matrix A to upper Hessenberg form H by an orthogonal similarity transformation: Q**T * A * Q = H .
pure subroutine, public	la_dgelq2 (m, n, a, lda, tau, work, info)
	DGELQ2: computes an LQ factorization of a real m-by-n matrix A: A = ( L 0 ) * Q where: Q is a n-by-n orthogonal matrix; L is a lower-triangular m-by-m matrix; 0 is a m-by-(n-m) zero matrix, if m < n.
pure subroutine, public	la_dgelqf (m, n, a, lda, tau, work, lwork, info)
	DGELQF: computes an LQ factorization of a real M-by-N matrix A: A = ( L 0 ) * Q where: Q is a N-by-N orthogonal matrix; L is a lower-triangular M-by-M matrix; 0 is a M-by-(N-M) zero matrix, if M < N.
pure recursive subroutine, public	la_dgelqt3 (m, n, a, lda, t, ldt, info)
	DGELQT3: recursively computes a LQ factorization of a real M-by-N matrix A, using the compact WY representation of Q. Based on the algorithm of Elmroth and Gustavson, IBM J. Res. Develop. Vol 44 No. 4 July 2000.
pure subroutine, public	la_dgeql2 (m, n, a, lda, tau, work, info)
	DGEQL2: computes a QL factorization of a real m by n matrix A: A = Q * L.
pure subroutine, public	la_dgeqlf (m, n, a, lda, tau, work, lwork, info)
	DGEQLF: computes a QL factorization of a real M-by-N matrix A: A = Q * L.
pure subroutine, public	la_dgeqr2 (m, n, a, lda, tau, work, info)
	DGEQR2: computes a QR factorization of a real m-by-n matrix A: A = Q * ( R ), ( 0 ) where: Q is a m-by-m orthogonal matrix; R is an upper-triangular n-by-n matrix; 0 is a (m-n)-by-n zero matrix, if m > n.
subroutine, public	la_dgeqr2p (m, n, a, lda, tau, work, info)
	DGEQR2P: computes a QR factorization of a real m-by-n matrix A: A = Q * ( R ), ( 0 ) where: Q is a m-by-m orthogonal matrix; R is an upper-triangular n-by-n matrix with nonnegative diagonal entries; 0 is a (m-n)-by-n zero matrix, if m > n.
pure subroutine, public	la_dgeqrf (m, n, a, lda, tau, work, lwork, info)
	DGEQRF: computes a QR factorization of a real M-by-N matrix A: A = Q * ( R ), ( 0 ) where: Q is a M-by-M orthogonal matrix; R is an upper-triangular N-by-N matrix; 0 is a (M-N)-by-N zero matrix, if M > N.
subroutine, public	la_dgeqrfp (m, n, a, lda, tau, work, lwork, info)
	DGEQR2P computes a QR factorization of a real M-by-N matrix A: A = Q * ( R ), ( 0 ) where: Q is a M-by-M orthogonal matrix; R is an upper-triangular N-by-N matrix with nonnegative diagonal entries; 0 is a (M-N)-by-N zero matrix, if M > N.
pure subroutine, public	la_dgeqrt2 (m, n, a, lda, t, ldt, info)
	DGEQRT2: computes a QR factorization of a real M-by-N matrix A, using the compact WY representation of Q.
pure recursive subroutine, public	la_dgeqrt3 (m, n, a, lda, t, ldt, info)
	DGEQRT3: recursively computes a QR factorization of a real M-by-N matrix A, using the compact WY representation of Q. Based on the algorithm of Elmroth and Gustavson, IBM J. Res. Develop. Vol 44 No. 4 July 2000.
pure subroutine, public	la_dgerfs (trans, n, nrhs, a, lda, af, ldaf, ipiv, b, ldb, x, ldx, ferr, berr, work, iwork, info)
	DGERFS: improves the computed solution to a system of linear equations and provides error bounds and backward error estimates for the solution.
pure subroutine, public	la_dgerq2 (m, n, a, lda, tau, work, info)
	DGERQ2: computes an RQ factorization of a real m by n matrix A: A = R * Q.
pure subroutine, public	la_dgerqf (m, n, a, lda, tau, work, lwork, info)
	DGERQF: computes an RQ factorization of a real M-by-N matrix A: A = R * Q.
pure subroutine, public	la_dgetrf (m, n, a, lda, ipiv, info)
	DGETRF: computes an LU factorization of a general M-by-N matrix A using partial pivoting with row interchanges. The factorization has the form A = P * L * U where P is a permutation matrix, L is lower triangular with unit diagonal elements (lower trapezoidal if m > n), and U is upper triangular (upper trapezoidal if m < n). This is the right-looking Level 3 BLAS version of the algorithm.
pure subroutine, public	la_dgghd3 (compq, compz, n, ilo, ihi, a, lda, b, ldb, q, ldq, z, ldz, work, lwork, info)
	DGGHD3: reduces a pair of real matrices (A,B) to generalized upper Hessenberg form using orthogonal transformations, where A is a general matrix and B is upper triangular. The form of the generalized eigenvalue problem is A*x = lambda*B*x, and B is typically made upper triangular by computing its QR factorization and moving the orthogonal matrix Q to the left side of the equation. This subroutine simultaneously reduces A to a Hessenberg matrix H: Q**T*A*Z = H and transforms B to another upper triangular matrix T: Q**T*B*Z = T in order to reduce the problem to its standard form H*y = lambda*T*y where y = Z**T*x. The orthogonal matrices Q and Z are determined as products of Givens rotations. They may either be formed explicitly, or they may be postmultiplied into input matrices Q1 and Z1, so that Q1 * A * Z1**T = (Q1*Q) * H * (Z1*Z)**T Q1 * B * Z1**T = (Q1*Q) * T * (Z1*Z)**T If Q1 is the orthogonal matrix from the QR factorization of B in the original equation A*x = lambda*B*x, then DGGHD3 reduces the original problem to generalized Hessenberg form. This is a blocked variant of DGGHRD, using matrix-matrix multiplications for parts of the computation to enhance performance.
pure subroutine, public	la_dggqrf (n, m, p, a, lda, taua, b, ldb, taub, work, lwork, info)
	DGGQRF: computes a generalized QR factorization of an N-by-M matrix A and an N-by-P matrix B: A = Q*R, B = Q*T*Z, where Q is an N-by-N orthogonal matrix, Z is a P-by-P orthogonal matrix, and R and T assume one of the forms: if N >= M, R = ( R11 ) M , or if N < M, R = ( R11 R12 ) N, ( 0 ) N-M N M-N M where R11 is upper triangular, and if N <= P, T = ( 0 T12 ) N, or if N > P, T = ( T11 ) N-P, P-N N ( T21 ) P P where T12 or T21 is upper triangular. In particular, if B is square and nonsingular, the GQR factorization of A and B implicitly gives the QR factorization of inv(B)*A: inv(B)*A = Z**T*(inv(T)*R) where inv(B) denotes the inverse of the matrix B, and Z**T denotes the transpose of the matrix Z.
pure subroutine, public	la_dggrqf (m, p, n, a, lda, taua, b, ldb, taub, work, lwork, info)
	DGGRQF: computes a generalized RQ factorization of an M-by-N matrix A and a P-by-N matrix B: A = R*Q, B = Z*T*Q, where Q is an N-by-N orthogonal matrix, Z is a P-by-P orthogonal matrix, and R and T assume one of the forms: if M <= N, R = ( 0 R12 ) M, or if M > N, R = ( R11 ) M-N, N-M M ( R21 ) N N where R12 or R21 is upper triangular, and if P >= N, T = ( T11 ) N , or if P < N, T = ( T11 T12 ) P, ( 0 ) P-N P N-P N where T11 is upper triangular. In particular, if B is square and nonsingular, the GRQ factorization of A and B implicitly gives the RQ factorization of A*inv(B): A*inv(B) = (R*inv(T))*Z**T where inv(B) denotes the inverse of the matrix B, and Z**T denotes the transpose of the matrix Z.
pure subroutine, public	la_dgsvj0 (jobv, m, n, a, lda, d, sva, mv, v, ldv, eps, sfmin, tol, nsweep, work, lwork, info)
	DGSVJ0: is called from DGESVJ as a pre-processor and that is its main purpose. It applies Jacobi rotations in the same way as DGESVJ does, but it does not check convergence (stopping criterion). Few tuning parameters (marked by [TP]) are available for the implementer.
pure subroutine, public	la_dgsvj1 (jobv, m, n, n1, a, lda, d, sva, mv, v, ldv, eps, sfmin, tol, nsweep, work, lwork, info)
	DGSVJ1: is called from DGESVJ as a pre-processor and that is its main purpose. It applies Jacobi rotations in the same way as DGESVJ does, but it targets only particular pivots and it does not check convergence (stopping criterion). Few tuning parameters (marked by [TP]) are available for the implementer. Further Details ~~~~~~~~~~~~~~~ DGSVJ1 applies few sweeps of Jacobi rotations in the column space of the input M-by-N matrix A. The pivot pairs are taken from the (1,2) off-diagonal block in the corresponding N-by-N Gram matrix A^T * A. The block-entries (tiles) of the (1,2) off-diagonal block are marked by the [x]'s in the following scheme: | * * * [x] [x] [x]| | * * * [x] [x] [x]| Row-cycling in the nblr-by-nblc [x] blocks. | * * * [x] [x] [x]| Row-cyclic pivoting inside each [x] block. |[x] [x] [x] * * * | |[x] [x] [x] * * * | |[x] [x] [x] * * * | In terms of the columns of A, the first N1 columns are rotated 'against' the remaining N-N1 columns, trying to increase the angle between the corresponding subspaces. The off-diagonal block is N1-by(N-N1) and it is tiled using quadratic tiles of side KBL. Here, KBL is a tuning parameter. The number of sweeps is given in NSWEEP and the orthogonality threshold is given in TOL.
pure subroutine, public	la_dgtcon (norm, n, dl, d, du, du2, ipiv, anorm, rcond, work, iwork, info)
	DGTCON: estimates the reciprocal of the condition number of a real tridiagonal matrix A using the LU factorization as computed by DGTTRF. An estimate is obtained for norm(inv(A)), and the reciprocal of the condition number is computed as RCOND = 1 / (ANORM * norm(inv(A))).
pure subroutine, public	la_dgtrfs (trans, n, nrhs, dl, d, du, dlf, df, duf, du2, ipiv, b, ldb, x, ldx, ferr, berr, work, iwork, info)
	DGTRFS: improves the computed solution to a system of linear equations when the coefficient matrix is tridiagonal, and provides error bounds and backward error estimates for the solution.
pure subroutine, public	la_dgtsvx (fact, trans, n, nrhs, dl, d, du, dlf, df, duf, du2, ipiv, b, ldb, x, ldx, rcond, ferr, berr, work, iwork, info)
	DGTSVX: uses the LU factorization to compute the solution to a real system of linear equations A * X = B or A**T * X = B, where A is a tridiagonal matrix of order N and X and B are N-by-NRHS matrices. Error bounds on the solution and a condition estimate are also provided.
subroutine, public	la_dhgeqz (job, compq, compz, n, ilo, ihi, h, ldh, t, ldt, alphar, alphai, beta, q, ldq, z, ldz, work, lwork, info)
	DHGEQZ: computes the eigenvalues of a real matrix pair (H,T), where H is an upper Hessenberg matrix and T is upper triangular, using the double-shift QZ method. Matrix pairs of this type are produced by the reduction to generalized upper Hessenberg form of a real matrix pair (A,B): A = Q1*H*Z1**T, B = Q1*T*Z1**T, as computed by DGGHRD. If JOB='S', then the Hessenberg-triangular pair (H,T) is also reduced to generalized Schur form, H = Q*S*Z**T, T = Q*P*Z**T, where Q and Z are orthogonal matrices, P is an upper triangular matrix, and S is a quasi-triangular matrix with 1-by-1 and 2-by-2 diagonal blocks. The 1-by-1 blocks correspond to real eigenvalues of the matrix pair (H,T) and the 2-by-2 blocks correspond to complex conjugate pairs of eigenvalues. Additionally, the 2-by-2 upper triangular diagonal blocks of P corresponding to 2-by-2 blocks of S are reduced to positive diagonal form, i.e., if S(j+1,j) is non-zero, then P(j+1,j) = P(j,j+1) = 0, P(j,j) > 0, and P(j+1,j+1) > 0. Optionally, the orthogonal matrix Q from the generalized Schur factorization may be postmultiplied into an input matrix Q1, and the orthogonal matrix Z may be postmultiplied into an input matrix Z1. If Q1 and Z1 are the orthogonal matrices from DGGHRD that reduced the matrix pair (A,B) to generalized upper Hessenberg form, then the output matrices Q1*Q and Z1*Z are the orthogonal factors from the generalized Schur factorization of (A,B): A = (Q1*Q)*S*(Z1*Z)**T, B = (Q1*Q)*P*(Z1*Z)**T. To avoid overflow, eigenvalues of the matrix pair (H,T) (equivalently, of (A,B)) are computed as a pair of values (alpha,beta), where alpha is complex and beta real. If beta is nonzero, lambda = alpha / beta is an eigenvalue of the generalized nonsymmetric eigenvalue problem (GNEP) A*x = lambda*B*x and if alpha is nonzero, mu = beta / alpha is an eigenvalue of the alternate form of the GNEP mu*A*y = B*y. Real eigenvalues can be read directly from the generalized Schur form: alpha = S(i,i), beta = P(i,i). Ref: C.B. Moler Eigenvalue Problems", SIAM J. Numer. Anal., 10(1973), pp. 241–256.
pure subroutine, public	la_dlabrd (m, n, nb, a, lda, d, e, tauq, taup, x, ldx, y, ldy)
	DLABRD: reduces the first NB rows and columns of a real general m by n matrix A to upper or lower bidiagonal form by an orthogonal transformation Q**T * A * P, and returns the matrices X and Y which are needed to apply the transformation to the unreduced part of A. If m >= n, A is reduced to upper bidiagonal form; if m < n, to lower bidiagonal form. This is an auxiliary routine called by DGEBRD.
pure subroutine, public	la_dladiv (a, b, c, d, p, q)
	DLADIV: performs complex division in real arithmetic a + i*b p + i*q = ------— c + i*d The algorithm is due to Michael Baudin and Robert L. Smith and can be found in the paper "A Robust Complex Division in Scilab".
pure subroutine, public	la_dlaed4 (n, i, d, z, delta, rho, dlam, info)
	This subroutine computes the I-th updated eigenvalue of a symmetric rank-one modification to a diagonal matrix whose elements are given in the array d, and that D(i) < D(j) for i < j and that RHO > 0. This is arranged by the calling routine, and is no loss in generality. The rank-one modified system is thus diag( D ) + RHO * Z * Z_transpose. where we assume the Euclidean norm of Z is 1. The method consists of approximating the rational functions in the secular equation by simpler interpolating rational functions.
pure subroutine, public	la_dlaed8 (icompq, k, n, qsiz, d, q, ldq, indxq, rho, cutpnt, z, dlamda, q2, ldq2, w, perm, givptr, givcol, givnum, indxp, indx, info)
	DLAED8: merges the two sets of eigenvalues together into a single sorted set. Then it tries to deflate the size of the problem. There are two ways in which deflation can occur: when two or more eigenvalues are close together or if there is a tiny element in the Z vector. For each such occurrence the order of the related secular equation problem is reduced by one.
pure subroutine, public	la_dlaed9 (k, kstart, kstop, n, d, q, ldq, rho, dlamda, w, s, lds, info)
	DLAED9: finds the roots of the secular equation, as defined by the values in D, Z, and RHO, between KSTART and KSTOP. It makes the appropriate calls to DLAED4 and then stores the new matrix of eigenvectors for use in calculating the next level of Z vectors.
pure subroutine, public	la_dlaein (rightv, noinit, n, h, ldh, wr, wi, vr, vi, b, ldb, work, eps3, smlnum, bignum, info)
	DLAEIN: uses inverse iteration to find a right or left eigenvector corresponding to the eigenvalue (WR,WI) of a real upper Hessenberg matrix H.
pure subroutine, public	la_dlagv2 (a, lda, b, ldb, alphar, alphai, beta, csl, snl, csr, snr)
	DLAGV2: computes the Generalized Schur factorization of a real 2-by-2 matrix pencil (A,B) where B is upper triangular. This routine computes orthogonal (rotation) matrices given by CSL, SNL and CSR, SNR such that 1) if the pencil (A,B) has two real eigenvalues (include 0/0 or 1/0 types), then [ a11 a12 ] := [ CSL SNL ] [ a11 a12 ] [ CSR -SNR ] [ 0 a22 ] [ -SNL CSL ] [ a21 a22 ] [ SNR CSR ] [ b11 b12 ] := [ CSL SNL ] [ b11 b12 ] [ CSR -SNR ] [ 0 b22 ] [ -SNL CSL ] [ 0 b22 ] [ SNR CSR ], 2) if the pencil (A,B) has a pair of complex conjugate eigenvalues, then [ a11 a12 ] := [ CSL SNL ] [ a11 a12 ] [ CSR -SNR ] [ a21 a22 ] [ -SNL CSL ] [ a21 a22 ] [ SNR CSR ] [ b11 0 ] := [ CSL SNL ] [ b11 b12 ] [ CSR -SNR ] [ 0 b22 ] [ -SNL CSL ] [ 0 b22 ] [ SNR CSR ] where b11 >= b22 > 0.
pure subroutine, public	la_dlahr2 (n, k, nb, a, lda, tau, t, ldt, y, ldy)
	DLAHR2: reduces the first NB columns of A real general n-BY-(n-k+1) matrix A so that elements below the k-th subdiagonal are zero. The reduction is performed by an orthogonal similarity transformation Q**T * A * Q. The routine returns the matrices V and T which determine Q as a block reflector I - V*T*V**T, and also the matrix Y = A * V * T. This is an auxiliary routine called by DGEHRD.
pure subroutine, public	la_dlaln2 (ltrans, na, nw, smin, ca, a, lda, d1, d2, b, ldb, wr, wi, x, ldx, scale, xnorm, info)
	DLALN2: solves a system of the form (ca A - w D ) X = s B or (ca A**T - w D) X = s B with possible scaling ("s") and perturbation of A. (A**T means A-transpose.) A is an NA x NA real matrix, ca is a real scalar, D is an NA x NA real diagonal matrix, w is a real or complex value, and X and B are NA x 1 matrices – real if w is real, complex if w is complex. NA may be 1 or 2. If w is complex, X and B are represented as NA x 2 matrices, the first column of each being the real part and the second being the imaginary part. "s" is a scaling factor (<= 1), computed by DLALN2, which is so chosen that X can be computed without overflow. X is further scaled if necessary to assure that norm(ca A - w D)*norm(X) is less than overflow. If both singular values of (ca A - w D) are less than SMIN, SMIN*identity will be used instead of (ca A - w D). If only one singular value is less than SMIN, one element of (ca A - w D) will be perturbed enough to make the smallest singular value roughly SMIN. If both singular values are at least SMIN, (ca A - w D) will not be perturbed. In any case, the perturbation will be at most some small multiple of max( SMIN, ulp*norm(ca A - w D) ). The singular values are computed by infinity-norm approximations, and thus will only be correct to a factor of 2 or so. Note: all input quantities are assumed to be smaller than overflow by a reasonable factor. (See BIGNUM.)
pure subroutine, public	la_dlals0 (icompq, nl, nr, sqre, nrhs, b, ldb, bx, ldbx, perm, givptr, givcol, ldgcol, givnum, ldgnum, poles, difl, difr, z, k, c, s, work, info)
	DLALS0: applies back the multiplying factors of either the left or the right singular vector matrix of a diagonal matrix appended by a row to the right hand side matrix B in solving the least squares problem using the divide-and-conquer SVD approach. For the left singular vector matrix, three types of orthogonal matrices are involved: (1L) Givens rotations: the number of such rotations is GIVPTR; the pairs of columns/rows they were applied to are stored in GIVCOL; and the C- and S-values of these rotations are stored in GIVNUM. (2L) Permutation. The (NL+1)-st row of B is to be moved to the first row, and for J=2:N, PERM(J)-th row of B is to be moved to the J-th row. (3L) The left singular vector matrix of the remaining matrix. For the right singular vector matrix, four types of orthogonal matrices are involved: (1R) The right singular vector matrix of the remaining matrix. (2R) If SQRE = 1, one extra Givens rotation to generate the right null space. (3R) The inverse transformation of (2L). (4R) The inverse transformation of (1L).
pure subroutine, public	la_dlamswlq (side, trans, m, n, k, mb, nb, a, lda, t, ldt, c, ldc, work, lwork, info)
	DLAMSWLQ: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q * C C * Q TRANS = 'T': Q**T * C C * Q**T where Q is a real orthogonal matrix defined as the product of blocked elementary reflectors computed by short wide LQ factorization (DLASWLQ)
pure subroutine, public	la_dlamtsqr (side, trans, m, n, k, mb, nb, a, lda, t, ldt, c, ldc, work, lwork, info)
	DLAMTSQR: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q * C C * Q TRANS = 'T': Q**T * C C * Q**T where Q is a real orthogonal matrix defined as the product of blocked elementary reflectors computed by tall skinny QR factorization (DLATSQR)
pure subroutine, public	la_dlanv2 (a, b, c, d, rt1r, rt1i, rt2r, rt2i, cs, sn)
	DLANV2: computes the Schur factorization of a real 2-by-2 nonsymmetric matrix in standard form: [ A B ] = [ CS -SN ] [ AA BB ] [ CS SN ] [ C D ] [ SN CS ] [ CC DD ] [-SN CS ] where either 1) CC = 0 so that AA and DD are real eigenvalues of the matrix, or 2) AA = DD and BB*CC < 0, so that AA + or - sqrt(BB*CC) are complex conjugate eigenvalues.
pure subroutine, public	la_dlapll (n, x, incx, y, incy, ssmin)
	Given two column vectors X and Y, let A = ( X Y ). The subroutine first computes the QR factorization of A = Q*R, and then computes the SVD of the 2-by-2 upper triangular matrix R. The smaller singular value of R is returned in SSMIN, which is used as the measurement of the linear dependency of the vectors X and Y.
pure subroutine, public	la_dlaqp2 (m, n, offset, a, lda, jpvt, tau, vn1, vn2, work)
	DLAQP2: computes a QR factorization with column pivoting of the block A(OFFSET+1:M,1:N). The block A(1:OFFSET,1:N) is accordingly pivoted, but not factorized.
pure subroutine, public	la_dlaqps (m, n, offset, nb, kb, a, lda, jpvt, tau, vn1, vn2, auxv, f, ldf)
	DLAQPS: computes a step of QR factorization with column pivoting of a real M-by-N matrix A by using Blas-3. It tries to factorize NB columns from A starting from the row OFFSET+1, and updates all of the matrix with Blas-3 xGEMM. In some cases, due to catastrophic cancellations, it cannot factorize NB columns. Hence, the actual number of factorized columns is returned in KB. Block A(1:OFFSET,1:N) is accordingly pivoted, but not factorized.
pure subroutine, public	la_dlaqr5 (wantt, wantz, kacc22, n, ktop, kbot, nshfts, sr, si, h, ldh, iloz, ihiz, z, ldz, v, ldv, u, ldu, nv, wv, ldwv, nh, wh, ldwh)
	DLAQR5:, called by DLAQR0, performs a single small-bulge multi-shift QR sweep.
subroutine, public	la_dlaqtr (ltran, lreal, n, t, ldt, b, w, scale, x, work, info)
	DLAQTR: solves the real quasi-triangular system op(T)*p = scale*c, if LREAL = .TRUE. or the complex quasi-triangular systems op(T + iB)*(p+iq) = scale*(c+id), if LREAL = .FALSE. in real arithmetic, where T is upper quasi-triangular. If LREAL = .FALSE., then the first diagonal block of T must be 1 by 1, B is the specially structured matrix B = [ b(1) b(2) ... b(n) ] [ w ] [ w ] [ . ] [ w ] op(A) = A or A**T, A**T denotes the transpose of matrix A. On input, X = [ c ]. On output, X = [ p ]. [ d ] [ q ] This subroutine is designed for the condition number estimation in routine DTRSNA.
pure subroutine, public	la_dlasd3 (nl, nr, sqre, k, d, q, ldq, dsigma, u, ldu, u2, ldu2, vt, ldvt, vt2, ldvt2, idxc, ctot, z, info)
	DLASD3: finds all the square roots of the roots of the secular equation, as defined by the values in D and Z. It makes the appropriate calls to DLASD4 and then updates the singular vectors by matrix multiplication. This code makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray XMP, Cray YMP, Cray C 90, or Cray 2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none. DLASD3 is called from DLASD1.
pure subroutine, public	la_dlasd6 (icompq, nl, nr, sqre, d, vf, vl, alpha, beta, idxq, perm, givptr, givcol, ldgcol, givnum, ldgnum, poles, difl, difr, z, k, c, s, work, iwork, info)
	DLASD6: computes the SVD of an updated upper bidiagonal matrix B obtained by merging two smaller ones by appending a row. This routine is used only for the problem which requires all singular values and optionally singular vector matrices in factored form. B is an N-by-M matrix with N = NL + NR + 1 and M = N + SQRE. A related subroutine, DLASD1, handles the case in which all singular values and singular vectors of the bidiagonal matrix are desired. DLASD6 computes the SVD as follows: ( D1(in) 0 0 0 ) B = U(in) * ( Z1**T a Z2**T b ) * VT(in) ( 0 0 D2(in) 0 ) = U(out) * ( D(out) 0) * VT(out) where Z**T = (Z1**T a Z2**T b) = u**T VT**T, and u is a vector of dimension M with ALPHA and BETA in the NL+1 and NL+2 th entries and zeros elsewhere; and the entry b is empty if SQRE = 0. The singular values of B can be computed using D1, D2, the first components of all the right singular vectors of the lower block, and the last components of all the right singular vectors of the upper block. These components are stored and updated in VF and VL, respectively, in DLASD6. Hence U and VT are not explicitly referenced. The singular values are stored in D. The algorithm consists of two stages: The first stage consists of deflating the size of the problem when there are multiple singular values or if there is a zero in the Z vector. For each such occurrence the dimension of the secular equation problem is reduced by one. This stage is performed by the routine DLASD7. The second stage consists of calculating the updated singular values. This is done by finding the roots of the secular equation via the routine DLASD4 (as called by DLASD8). This routine also updates VF and VL and computes the distances between the updated singular values and the old singular values. DLASD6 is called from DLASDA.
pure subroutine, public	la_dopgtr (uplo, n, ap, tau, q, ldq, work, info)
	DOPGTR: generates a real orthogonal matrix Q which is defined as the product of n-1 elementary reflectors H(i) of order n, as returned by DSPTRD using packed storage: if UPLO = 'U', Q = H(n-1) . . . H(2) H(1), if UPLO = 'L', Q = H(1) H(2) . . . H(n-1).
pure subroutine, public	la_dopmtr (side, uplo, trans, m, n, ap, tau, c, ldc, work, info)
	DOPMTR: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q * C C * Q TRANS = 'T': Q**T * C C * Q**T where Q is a real orthogonal matrix of order nq, with nq = m if SIDE = 'L' and nq = n if SIDE = 'R'. Q is defined as the product of nq-1 elementary reflectors, as returned by DSPTRD using packed storage: if UPLO = 'U', Q = H(nq-1) . . . H(2) H(1); if UPLO = 'L', Q = H(1) H(2) . . . H(nq-1).
subroutine, public	la_dorbdb1 (m, p, q, x11, ldx11, x21, ldx21, theta, phi, taup1, taup2, tauq1, work, lwork, info)
	DORBDB1: simultaneously bidiagonalizes the blocks of a tall and skinny matrix X with orthonomal columns: [ B11 ] [ X11 ] [ P1 | ] [ 0 ] [--—] = [------—] [--—] Q1**T . [ X21 ] [ | P2 ] [ B21 ] [ 0 ] X11 is P-by-Q, and X21 is (M-P)-by-Q. Q must be no larger than P, M-P, or M-Q. Routines DORBDB2, DORBDB3, and DORBDB4 handle cases in which Q is not the minimum dimension. The orthogonal matrices P1, P2, and Q1 are P-by-P, (M-P)-by-(M-P), and (M-Q)-by-(M-Q), respectively. They are represented implicitly by Householder vectors. B11 and B12 are Q-by-Q bidiagonal matrices represented implicitly by angles THETA, PHI.
subroutine, public	la_dorbdb2 (m, p, q, x11, ldx11, x21, ldx21, theta, phi, taup1, taup2, tauq1, work, lwork, info)
	DORBDB2: simultaneously bidiagonalizes the blocks of a tall and skinny matrix X with orthonomal columns: [ B11 ] [ X11 ] [ P1 | ] [ 0 ] [--—] = [------—] [--—] Q1**T . [ X21 ] [ | P2 ] [ B21 ] [ 0 ] X11 is P-by-Q, and X21 is (M-P)-by-Q. P must be no larger than M-P, Q, or M-Q. Routines DORBDB1, DORBDB3, and DORBDB4 handle cases in which P is not the minimum dimension. The orthogonal matrices P1, P2, and Q1 are P-by-P, (M-P)-by-(M-P), and (M-Q)-by-(M-Q), respectively. They are represented implicitly by Householder vectors. B11 and B12 are P-by-P bidiagonal matrices represented implicitly by angles THETA, PHI.
subroutine, public	la_dorbdb3 (m, p, q, x11, ldx11, x21, ldx21, theta, phi, taup1, taup2, tauq1, work, lwork, info)
	DORBDB3: simultaneously bidiagonalizes the blocks of a tall and skinny matrix X with orthonomal columns: [ B11 ] [ X11 ] [ P1 | ] [ 0 ] [--—] = [------—] [--—] Q1**T . [ X21 ] [ | P2 ] [ B21 ] [ 0 ] X11 is P-by-Q, and X21 is (M-P)-by-Q. M-P must be no larger than P, Q, or M-Q. Routines DORBDB1, DORBDB2, and DORBDB4 handle cases in which M-P is not the minimum dimension. The orthogonal matrices P1, P2, and Q1 are P-by-P, (M-P)-by-(M-P), and (M-Q)-by-(M-Q), respectively. They are represented implicitly by Householder vectors. B11 and B12 are (M-P)-by-(M-P) bidiagonal matrices represented implicitly by angles THETA, PHI.
subroutine, public	la_dorbdb4 (m, p, q, x11, ldx11, x21, ldx21, theta, phi, taup1, taup2, tauq1, phantom, work, lwork, info)
	DORBDB4: simultaneously bidiagonalizes the blocks of a tall and skinny matrix X with orthonomal columns: [ B11 ] [ X11 ] [ P1 | ] [ 0 ] [--—] = [------—] [--—] Q1**T . [ X21 ] [ | P2 ] [ B21 ] [ 0 ] X11 is P-by-Q, and X21 is (M-P)-by-Q. M-Q must be no larger than P, M-P, or Q. Routines DORBDB1, DORBDB2, and DORBDB3 handle cases in which M-Q is not the minimum dimension. The orthogonal matrices P1, P2, and Q1 are P-by-P, (M-P)-by-(M-P), and (M-Q)-by-(M-Q), respectively. They are represented implicitly by Householder vectors. B11 and B12 are (M-Q)-by-(M-Q) bidiagonal matrices represented implicitly by angles THETA, PHI.
subroutine, public	la_dorcsd2by1 (jobu1, jobu2, jobv1t, m, p, q, x11, ldx11, x21, ldx21, theta, u1, ldu1, u2, ldu2, v1t, ldv1t, work, lwork, iwork, info)
	DORCSD2BY1: computes the CS decomposition of an M-by-Q matrix X with orthonormal columns that has been partitioned into a 2-by-1 block structure: [ I1 0 0 ] [ 0 C 0 ] [ X11 ] [ U1 | ] [ 0 0 0 ] X = [--—] = [------—] [-------—] V1**T . [ X21 ] [ | U2 ] [ 0 0 0 ] [ 0 S 0 ] [ 0 0 I2] X11 is P-by-Q. The orthogonal matrices U1, U2, and V1 are P-by-P, (M-P)-by-(M-P), and Q-by-Q, respectively. C and S are R-by-R nonnegative diagonal matrices satisfying C^2 + S^2 = I, in which R = MIN(P,M-P,Q,M-Q). I1 is a K1-by-K1 identity matrix and I2 is a K2-by-K2 identity matrix, where K1 = MAX(Q+P-M,0), K2 = MAX(Q-P,0).
pure subroutine, public	la_dorgtr (uplo, n, a, lda, tau, work, lwork, info)
	DORGTR: generates a real orthogonal matrix Q which is defined as the product of n-1 elementary reflectors of order N, as returned by DSYTRD: if UPLO = 'U', Q = H(n-1) . . . H(2) H(1), if UPLO = 'L', Q = H(1) H(2) . . . H(n-1).
pure subroutine, public	la_dorgtsqr (m, n, mb, nb, a, lda, t, ldt, work, lwork, info)
	DORGTSQR: generates an M-by-N real matrix Q_out with orthonormal columns, which are the first N columns of a product of real orthogonal matrices of order M which are returned by DLATSQR Q_out = first_N_columns_of( Q(1)_in * Q(2)_in * ... * Q(k)_in ). See the documentation for DLATSQR.
pure subroutine, public	la_dormtr (side, uplo, trans, m, n, a, lda, tau, c, ldc, work, lwork, info)
	DORMTR: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q * C C * Q TRANS = 'T': Q**T * C C * Q**T where Q is a real orthogonal matrix of order nq, with nq = m if SIDE = 'L' and nq = n if SIDE = 'R'. Q is defined as the product of nq-1 elementary reflectors, as returned by DSYTRD: if UPLO = 'U', Q = H(nq-1) . . . H(2) H(1); if UPLO = 'L', Q = H(1) H(2) . . . H(nq-1).
pure subroutine, public	la_dpbtrf (uplo, n, kd, ab, ldab, info)
	DPBTRF: computes the Cholesky factorization of a real symmetric positive definite band matrix A. The factorization has the form A = U**T * U, if UPLO = 'U', or A = L * L**T, if UPLO = 'L', where U is an upper triangular matrix and L is lower triangular.
pure subroutine, public	la_dpftri (transr, uplo, n, a, info)
	DPFTRI: computes the inverse of a (real) symmetric positive definite matrix A using the Cholesky factorization A = U**T*U or A = L*L**T computed by DPFTRF.
pure subroutine, public	la_dpotrf (uplo, n, a, lda, info)
	DPOTRF: computes the Cholesky factorization of a real symmetric positive definite matrix A. The factorization has the form A = U**T * U, if UPLO = 'U', or A = L * L**T, if UPLO = 'L', where U is an upper triangular matrix and L is lower triangular. This is the block version of the algorithm, calling Level 3 BLAS.
pure subroutine, public	la_dptrfs (n, nrhs, d, e, df, ef, b, ldb, x, ldx, ferr, berr, work, info)
	DPTRFS: improves the computed solution to a system of linear equations when the coefficient matrix is symmetric positive definite and tridiagonal, and provides error bounds and backward error estimates for the solution.
pure subroutine, public	la_dptsv (n, nrhs, d, e, b, ldb, info)
	DPTSV: computes the solution to a real system of linear equations A*X = B, where A is an N-by-N symmetric positive definite tridiagonal matrix, and X and B are N-by-NRHS matrices. A is factored as A = L*D*L**T, and the factored form of A is then used to solve the system of equations.
pure subroutine, public	la_dptsvx (fact, n, nrhs, d, e, df, ef, b, ldb, x, ldx, rcond, ferr, berr, work, info)
	DPTSVX: uses the factorization A = L*D*L**T to compute the solution to a real system of linear equations A*X = B, where A is an N-by-N symmetric positive definite tridiagonal matrix and X and B are N-by-NRHS matrices. Error bounds on the solution and a condition estimate are also provided.
subroutine, public	la_dsbev (jobz, uplo, n, kd, ab, ldab, w, z, ldz, work, info)
	DSBEV: computes all the eigenvalues and, optionally, eigenvectors of a real symmetric band matrix A.
subroutine, public	la_dsbevx (jobz, range, uplo, n, kd, ab, ldab, q, ldq, vl, vu, il, iu, abstol, m, w, z, ldz, work, iwork, ifail, info)
	DSBEVX: computes selected eigenvalues and, optionally, eigenvectors of a real symmetric band matrix A. Eigenvalues and eigenvectors can be selected by specifying either a range of values or a range of indices for the desired eigenvalues.
pure subroutine, public	la_dsbgv (jobz, uplo, n, ka, kb, ab, ldab, bb, ldbb, w, z, ldz, work, info)
	DSBGV: computes all the eigenvalues, and optionally, the eigenvectors of a real generalized symmetric-definite banded eigenproblem, of the form A*x=(lambda)*B*x. Here A and B are assumed to be symmetric and banded, and B is also positive definite.
pure subroutine, public	la_dsbgvx (jobz, range, uplo, n, ka, kb, ab, ldab, bb, ldbb, q, ldq, vl, vu, il, iu, abstol, m, w, z, ldz, work, iwork, ifail, info)
	DSBGVX: computes selected eigenvalues, and optionally, eigenvectors of a real generalized symmetric-definite banded eigenproblem, of the form A*x=(lambda)*B*x. Here A and B are assumed to be symmetric and banded, and B is also positive definite. Eigenvalues and eigenvectors can be selected by specifying either all eigenvalues, a range of values or a range of indices for the desired eigenvalues.
subroutine, public	la_dsgesv (n, nrhs, a, lda, ipiv, b, ldb, x, ldx, work, swork, iter, info)
	DSGESV: computes the solution to a real system of linear equations A * X = B, where A is an N-by-N matrix and X and B are N-by-NRHS matrices. DSGESV first attempts to factorize the matrix in SINGLE PRECISION and use this factorization within an iterative refinement procedure to produce a solution with DOUBLE PRECISION normwise backward error quality (see below). If the approach fails the method switches to a DOUBLE PRECISION factorization and solve. The iterative refinement is not going to be a winning strategy if the ratio SINGLE PRECISION performance over DOUBLE PRECISION performance is too small. A reasonable strategy should take the number of right-hand sides and the size of the matrix into account. This might be done with a call to ILAENV in the future. Up to now, we always try iterative refinement. The iterative refinement process is stopped if ITER > ITERMAX or for all the RHS we have: RNRM < SQRT(N)*XNRM*ANRM*EPS*BWDMAX where o ITER is the number of the current iteration in the iterative refinement process o RNRM is the infinity-norm of the residual o XNRM is the infinity-norm of the solution o ANRM is the infinity-operator-norm of the matrix A o EPS is the machine epsilon returned by DLAMCH('Epsilon') The value ITERMAX and BWDMAX are fixed to 30 and 1.0D+00 respectively.
subroutine, public	la_dspev (jobz, uplo, n, ap, w, z, ldz, work, info)
	DSPEV: computes all the eigenvalues and, optionally, eigenvectors of a real symmetric matrix A in packed storage.
subroutine, public	la_dspevx (jobz, range, uplo, n, ap, vl, vu, il, iu, abstol, m, w, z, ldz, work, iwork, ifail, info)
	DSPEVX: computes selected eigenvalues and, optionally, eigenvectors of a real symmetric matrix A in packed storage. Eigenvalues/vectors can be selected by specifying either a range of values or a range of indices for the desired eigenvalues.
subroutine, public	la_dspgv (itype, jobz, uplo, n, ap, bp, w, z, ldz, work, info)
	DSPGV: computes all the eigenvalues and, optionally, the eigenvectors of a real generalized symmetric-definite eigenproblem, of the form A*x=(lambda)*B*x, A*Bx=(lambda)*x, or B*A*x=(lambda)*x. Here A and B are assumed to be symmetric, stored in packed format, and B is also positive definite.
subroutine, public	la_dspgvx (itype, jobz, range, uplo, n, ap, bp, vl, vu, il, iu, abstol, m, w, z, ldz, work, iwork, ifail, info)
	DSPGVX: computes selected eigenvalues, and optionally, eigenvectors of a real generalized symmetric-definite eigenproblem, of the form A*x=(lambda)*B*x, A*Bx=(lambda)*x, or B*A*x=(lambda)*x. Here A and B are assumed to be symmetric, stored in packed storage, and B is also positive definite. Eigenvalues and eigenvectors can be selected by specifying either a range of values or a range of indices for the desired eigenvalues.
subroutine, public	la_dsposv (uplo, n, nrhs, a, lda, b, ldb, x, ldx, work, swork, iter, info)
	DSPOSV: computes the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric positive definite matrix and X and B are N-by-NRHS matrices. DSPOSV first attempts to factorize the matrix in SINGLE PRECISION and use this factorization within an iterative refinement procedure to produce a solution with DOUBLE PRECISION normwise backward error quality (see below). If the approach fails the method switches to a DOUBLE PRECISION factorization and solve. The iterative refinement is not going to be a winning strategy if the ratio SINGLE PRECISION performance over DOUBLE PRECISION performance is too small. A reasonable strategy should take the number of right-hand sides and the size of the matrix into account. This might be done with a call to ILAENV in the future. Up to now, we always try iterative refinement. The iterative refinement process is stopped if ITER > ITERMAX or for all the RHS we have: RNRM < SQRT(N)*XNRM*ANRM*EPS*BWDMAX where o ITER is the number of the current iteration in the iterative refinement process o RNRM is the infinity-norm of the residual o XNRM is the infinity-norm of the solution o ANRM is the infinity-operator-norm of the matrix A o EPS is the machine epsilon returned by DLAMCH('Epsilon') The value ITERMAX and BWDMAX are fixed to 30 and 1.0D+00 respectively.
subroutine, public	la_dsyev (jobz, uplo, n, a, lda, w, work, lwork, info)
	DSYEV: computes all eigenvalues and, optionally, eigenvectors of a real symmetric matrix A.
subroutine, public	la_dsyevx (jobz, range, uplo, n, a, lda, vl, vu, il, iu, abstol, m, w, z, ldz, work, lwork, iwork, ifail, info)
	DSYEVX: computes selected eigenvalues and, optionally, eigenvectors of a real symmetric matrix A. Eigenvalues and eigenvectors can be selected by specifying either a range of values or a range of indices for the desired eigenvalues.
subroutine, public	la_dsygv (itype, jobz, uplo, n, a, lda, b, ldb, w, work, lwork, info)
	DSYGV: computes all the eigenvalues, and optionally, the eigenvectors of a real generalized symmetric-definite eigenproblem, of the form A*x=(lambda)*B*x, A*Bx=(lambda)*x, or B*A*x=(lambda)*x. Here A and B are assumed to be symmetric and B is also positive definite.
subroutine, public	la_dsygvx (itype, jobz, range, uplo, n, a, lda, b, ldb, vl, vu, il, iu, abstol, m, w, z, ldz, work, lwork, iwork, ifail, info)
	DSYGVX: computes selected eigenvalues, and optionally, eigenvectors of a real generalized symmetric-definite eigenproblem, of the form A*x=(lambda)*B*x, A*Bx=(lambda)*x, or B*A*x=(lambda)*x. Here A and B are assumed to be symmetric and B is also positive definite. Eigenvalues and eigenvectors can be selected by specifying either a range of values or a range of indices for the desired eigenvalues.
pure subroutine, public	la_dsysv (uplo, n, nrhs, a, lda, ipiv, b, ldb, work, lwork, info)
	DSYSV: computes the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric matrix and X and B are N-by-NRHS matrices. The diagonal pivoting method is used to factor A as A = U * D * U**T, if UPLO = 'U', or A = L * D * L**T, if UPLO = 'L', where U (or L) is a product of permutation and unit upper (lower) triangular matrices, and D is symmetric and block diagonal with 1-by-1 and 2-by-2 diagonal blocks. The factored form of A is then used to solve the system of equations A * X = B.
subroutine, public	la_dsysvx (fact, uplo, n, nrhs, a, lda, af, ldaf, ipiv, b, ldb, x, ldx, rcond, ferr, berr, work, lwork, iwork, info)
	DSYSVX: uses the diagonal pivoting factorization to compute the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric matrix and X and B are N-by-NRHS matrices. Error bounds on the solution and a condition estimate are also provided.
pure subroutine, public	la_dsytrd_sy2sb (uplo, n, kd, a, lda, ab, ldab, tau, work, lwork, info)
	DSYTRD_SY2SB: reduces a real symmetric matrix A to real symmetric band-diagonal form AB by a orthogonal similarity transformation: Q**T * A * Q = AB.
pure subroutine, public	la_dtgevc (side, howmny, select, n, s, lds, p, ldp, vl, ldvl, vr, ldvr, mm, m, work, info)
	DTGEVC: computes some or all of the right and/or left eigenvectors of a pair of real matrices (S,P), where S is a quasi-triangular matrix and P is upper triangular. Matrix pairs of this type are produced by the generalized Schur factorization of a matrix pair (A,B): A = Q*S*Z**T, B = Q*P*Z**T as computed by DGGHRD + DHGEQZ. The right eigenvector x and the left eigenvector y of (S,P) corresponding to an eigenvalue w are defined by: S*x = w*P*x, (y**H)*S = w*(y**H)*P, where y**H denotes the conjugate tranpose of y. The eigenvalues are not input to this routine, but are computed directly from the diagonal blocks of S and P. This routine returns the matrices X and/or Y of right and left eigenvectors of (S,P), or the products Z*X and/or Q*Y, where Z and Q are input matrices. If Q and Z are the orthogonal factors from the generalized Schur factorization of a matrix pair (A,B), then Z*X and Q*Y are the matrices of right and left eigenvectors of (A,B).
pure subroutine, public	la_dtgex2 (wantq, wantz, n, a, lda, b, ldb, q, ldq, z, ldz, j1, n1, n2, work, lwork, info)
	DTGEX2: swaps adjacent diagonal blocks (A11, B11) and (A22, B22) of size 1-by-1 or 2-by-2 in an upper (quasi) triangular matrix pair (A, B) by an orthogonal equivalence transformation. (A, B) must be in generalized real Schur canonical form (as returned by DGGES), i.e. A is block upper triangular with 1-by-1 and 2-by-2 diagonal blocks. B is upper triangular. Optionally, the matrices Q and Z of generalized Schur vectors are updated. Q(in) * A(in) * Z(in)**T = Q(out) * A(out) * Z(out)**T Q(in) * B(in) * Z(in)**T = Q(out) * B(out) * Z(out)**T.
pure subroutine, public	la_dtgexc (wantq, wantz, n, a, lda, b, ldb, q, ldq, z, ldz, ifst, ilst, work, lwork, info)
	DTGEXC: reorders the generalized real Schur decomposition of a real matrix pair (A,B) using an orthogonal equivalence transformation (A, B) = Q * (A, B) * Z**T, so that the diagonal block of (A, B) with row index IFST is moved to row ILST. (A, B) must be in generalized real Schur canonical form (as returned by DGGES), i.e. A is block upper triangular with 1-by-1 and 2-by-2 diagonal blocks. B is upper triangular. Optionally, the matrices Q and Z of generalized Schur vectors are updated. Q(in) * A(in) * Z(in)**T = Q(out) * A(out) * Z(out)**T Q(in) * B(in) * Z(in)**T = Q(out) * B(out) * Z(out)**T.
pure subroutine, public	la_dtgsen (ijob, wantq, wantz, select, n, a, lda, b, ldb, alphar, alphai, beta, q, ldq, z, ldz, m, pl, pr, dif, work, lwork, iwork, liwork, info)
	DTGSEN: reorders the generalized real Schur decomposition of a real matrix pair (A, B) (in terms of an orthonormal equivalence trans- formation Q**T * (A, B) * Z), so that a selected cluster of eigenvalues appears in the leading diagonal blocks of the upper quasi-triangular matrix A and the upper triangular B. The leading columns of Q and Z form orthonormal bases of the corresponding left and right eigen- spaces (deflating subspaces). (A, B) must be in generalized real Schur canonical form (as returned by DGGES), i.e. A is block upper triangular with 1-by-1 and 2-by-2 diagonal blocks. B is upper triangular. DTGSEN also computes the generalized eigenvalues w(j) = (ALPHAR(j) + i*ALPHAI(j))/BETA(j) of the reordered matrix pair (A, B). Optionally, DTGSEN computes the estimates of reciprocal condition numbers for eigenvalues and eigenspaces. These are Difu[(A11,B11), (A22,B22)] and Difl[(A11,B11), (A22,B22)], i.e. the separation(s) between the matrix pairs (A11, B11) and (A22,B22) that correspond to the selected cluster and the eigenvalues outside the cluster, resp., and norms of "projections" onto left and right eigenspaces w.r.t. the selected cluster in the (1,1)-block.
pure subroutine, public	la_dtgsja (jobu, jobv, jobq, m, p, n, k, l, a, lda, b, ldb, tola, tolb, alpha, beta, u, ldu, v, ldv, q, ldq, work, ncycle, info)
	DTGSJA: computes the generalized singular value decomposition (GSVD) of two real upper triangular (or trapezoidal) matrices A and B. On entry, it is assumed that matrices A and B have the following forms, which may be obtained by the preprocessing subroutine DGGSVP from a general M-by-N matrix A and P-by-N matrix B: N-K-L K L A = K ( 0 A12 A13 ) if M-K-L >= 0; L ( 0 0 A23 ) M-K-L ( 0 0 0 ) N-K-L K L A = K ( 0 A12 A13 ) if M-K-L < 0; M-K ( 0 0 A23 ) N-K-L K L B = L ( 0 0 B13 ) P-L ( 0 0 0 ) where the K-by-K matrix A12 and L-by-L matrix B13 are nonsingular upper triangular; A23 is L-by-L upper triangular if M-K-L >= 0, otherwise A23 is (M-K)-by-L upper trapezoidal. On exit, U**T A*Q = D1( 0 R ), V**T B*Q = D2( 0 R ), where U, V and Q are orthogonal matrices. R is a nonsingular upper triangular matrix, and D1 and D2 are `‘diagonal’' matrices, which are of the following structures: If M-K-L >= 0, K L D1 = K ( I 0 ) L ( 0 C ) M-K-L ( 0 0 ) K L D2 = L ( 0 S ) P-L ( 0 0 ) N-K-L K L ( 0 R ) = K ( 0 R11 R12 ) K L ( 0 0 R22 ) L where C = diag( ALPHA(K+1), ... , ALPHA(K+L) ), S = diag( BETA(K+1), ... , BETA(K+L) ), C**2 + S**2 = I. R is stored in A(1:K+L,N-K-L+1:N) on exit. If M-K-L < 0, K M-K K+L-M D1 = K ( I 0 0 ) M-K ( 0 C 0 ) K M-K K+L-M D2 = M-K ( 0 S 0 ) K+L-M ( 0 0 I ) P-L ( 0 0 0 ) N-K-L K M-K K+L-M ( 0 R ) = K ( 0 R11 R12 R13 ) M-K ( 0 0 R22 R23 ) K+L-M ( 0 0 0 R33 ) where C = diag( ALPHA(K+1), ... , ALPHA(M) ), S = diag( BETA(K+1), ... , BETA(M) ), C**2 + S**2 = I. R = ( R11 R12 R13 ) is stored in A(1:M, N-K-L+1:N) and R33 is stored ( 0 R22 R23 ) in B(M-K+1:L,N+M-K-L+1:N) on exit. The computation of the orthogonal transformation matrices U, V or Q is optional. These matrices may either be formed explicitly, or they may be postmultiplied into input matrices U1, V1, or Q1.
pure subroutine, public	la_dtgsna (job, howmny, select, n, a, lda, b, ldb, vl, ldvl, vr, ldvr, s, dif, mm, m, work, lwork, iwork, info)
	DTGSNA: estimates reciprocal condition numbers for specified eigenvalues and/or eigenvectors of a matrix pair (A, B) in generalized real Schur canonical form (or of any matrix pair (Q*A*Z**T, Q*B*Z**T) with orthogonal matrices Q and Z, where Z**T denotes the transpose of Z. (A, B) must be in generalized real Schur form (as returned by DGGES), i.e. A is block upper triangular with 1-by-1 and 2-by-2 diagonal blocks. B is upper triangular.
pure subroutine, public	la_dtplqt (m, n, l, mb, a, lda, b, ldb, t, ldt, work, info)
	DTPLQT: computes a blocked LQ factorization of a real "triangular-pentagonal" matrix C, which is composed of a triangular block A and pentagonal block B, using the compact WY representation for Q.
pure subroutine, public	la_dtpqrt (m, n, l, nb, a, lda, b, ldb, t, ldt, work, info)
	DTPQRT: computes a blocked QR factorization of a real "triangular-pentagonal" matrix C, which is composed of a triangular block A and pentagonal block B, using the compact WY representation for Q.
pure subroutine, public	la_dtrevc (side, howmny, select, n, t, ldt, vl, ldvl, vr, ldvr, mm, m, work, info)
	DTREVC: computes some or all of the right and/or left eigenvectors of a real upper quasi-triangular matrix T. Matrices of this type are produced by the Schur factorization of a real general matrix: A = Q*T*Q**T, as computed by DHSEQR. The right eigenvector x and the left eigenvector y of T corresponding to an eigenvalue w are defined by: T*x = w*x, (y**H)*T = w*(y**H) where y**H denotes the conjugate transpose of y. The eigenvalues are not input to this routine, but are read directly from the diagonal blocks of T. This routine returns the matrices X and/or Y of right and left eigenvectors of T, or the products Q*X and/or Q*Y, where Q is an input matrix. If Q is the orthogonal factor that reduces a matrix A to Schur form T, then Q*X and Q*Y are the matrices of right and left eigenvectors of A.
pure subroutine, public	la_dtrevc3 (side, howmny, select, n, t, ldt, vl, ldvl, vr, ldvr, mm, m, work, lwork, info)
	DTREVC3: computes some or all of the right and/or left eigenvectors of a real upper quasi-triangular matrix T. Matrices of this type are produced by the Schur factorization of a real general matrix: A = Q*T*Q**T, as computed by DHSEQR. The right eigenvector x and the left eigenvector y of T corresponding to an eigenvalue w are defined by: T*x = w*x, (y**T)*T = w*(y**T) where y**T denotes the transpose of the vector y. The eigenvalues are not input to this routine, but are read directly from the diagonal blocks of T. This routine returns the matrices X and/or Y of right and left eigenvectors of T, or the products Q*X and/or Q*Y, where Q is an input matrix. If Q is the orthogonal factor that reduces a matrix A to Schur form T, then Q*X and Q*Y are the matrices of right and left eigenvectors of A. This uses a Level 3 BLAS version of the back transformation.
subroutine, public	la_dtrsyl (trana, tranb, isgn, m, n, a, lda, b, ldb, c, ldc, scale, info)
	DTRSYL: solves the real Sylvester matrix equation: op(A)*X + X*op(B) = scale*C or op(A)*X - X*op(B) = scale*C, where op(A) = A or A**T, and A and B are both upper quasi- triangular. A is M-by-M and B is N-by-N; the right hand side C and the solution X are M-by-N; and scale is an output scale factor, set <= 1 to avoid overflow in X. A and B must be in Schur canonical form (as returned by DHSEQR), that is, block upper triangular with 1-by-1 and 2-by-2 diagonal blocks; each 2-by-2 diagonal block has its diagonal elements equal and its off-diagonal elements of opposite sign.
pure subroutine, public	la_dgebrd (m, n, a, lda, d, e, tauq, taup, work, lwork, info)
	DGEBRD: reduces a general real M-by-N matrix A to upper or lower bidiagonal form B by an orthogonal transformation: Q**T * A * P = B. If m >= n, B is upper bidiagonal; if m < n, B is lower bidiagonal.
pure subroutine, public	la_dgehrd (n, ilo, ihi, a, lda, tau, work, lwork, info)
	DGEHRD: reduces a real general matrix A to upper Hessenberg form H by an orthogonal similarity transformation: Q**T * A * Q = H .
pure subroutine, public	la_dgelqt (m, n, mb, a, lda, t, ldt, work, info)
	DGELQT: computes a blocked LQ factorization of a real M-by-N matrix A using the compact WY representation of Q.
subroutine, public	la_dgels (trans, m, n, nrhs, a, lda, b, ldb, work, lwork, info)
	DGELS: solves overdetermined or underdetermined real linear systems involving an M-by-N matrix A, or its transpose, using a QR or LQ factorization of A. It is assumed that A has full rank. The following options are provided:
pure subroutine, public	la_dgemlq (side, trans, m, n, k, a, lda, t, tsize, c, ldc, work, lwork, info)
	DGEMLQ: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q * C C * Q TRANS = 'T': Q**T * C C * Q**T where Q is a real orthogonal matrix defined as the product of blocked elementary reflectors computed by short wide LQ factorization (DGELQ)
pure subroutine, public	la_dgemqr (side, trans, m, n, k, a, lda, t, tsize, c, ldc, work, lwork, info)
	DGEMQR: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q * C C * Q TRANS = 'T': Q**T * C C * Q**T where Q is a real orthogonal matrix defined as the product of blocked elementary reflectors computed by tall skinny QR factorization (DGEQR)
pure subroutine, public	la_dgeqp3 (m, n, a, lda, jpvt, tau, work, lwork, info)
	DGEQP3: computes a QR factorization with column pivoting of a matrix A: A*P = Q*R using Level 3 BLAS.
pure subroutine, public	la_dgeqrt (m, n, nb, a, lda, t, ldt, work, info)
	DGEQRT: computes a blocked QR factorization of a real M-by-N matrix A using the compact WY representation of Q.
pure subroutine, public	la_dgesv (n, nrhs, a, lda, ipiv, b, ldb, info)
	DGESV: computes the solution to a real system of linear equations A * X = B, where A is an N-by-N matrix and X and B are N-by-NRHS matrices. The LU decomposition with partial pivoting and row interchanges is used to factor A as A = P * L * U, where P is a permutation matrix, L is unit lower triangular, and U is upper triangular. The factored form of A is then used to solve the system of equations A * X = B.
pure subroutine, public	la_dgesvj (joba, jobu, jobv, m, n, a, lda, sva, mv, v, ldv, work, lwork, info)
	DGESVJ: computes the singular value decomposition (SVD) of a real M-by-N matrix A, where M >= N. The SVD of A is written as [++] [xx] [x0] [xx] A = U * SIGMA * V^t, [++] = [xx] * [ox] * [xx] [++] [xx] where SIGMA is an N-by-N diagonal matrix, U is an M-by-N orthonormal matrix, and V is an N-by-N orthogonal matrix. The diagonal elements of SIGMA are the singular values of A. The columns of U and V are the left and the right singular vectors of A, respectively. DGESVJ can sometimes compute tiny singular values and their singular vectors much more accurately than other SVD routines, see below under Further Details.
subroutine, public	la_dgesvx (fact, trans, n, nrhs, a, lda, af, ldaf, ipiv, equed, r, c, b, ldb, x, ldx, rcond, ferr, berr, work, iwork, info)
	DGESVX: uses the LU factorization to compute the solution to a real system of linear equations A * X = B, where A is an N-by-N matrix and X and B are N-by-NRHS matrices. Error bounds on the solution and a condition estimate are also provided.
subroutine, public	la_dgges (jobvsl, jobvsr, sort, selctg, n, a, lda, b, ldb, sdim, alphar, alphai, beta, vsl, ldvsl, vsr, ldvsr, work, lwork, bwork, info)
	DGGES: computes for a pair of N-by-N real nonsymmetric matrices (A,B), the generalized eigenvalues, the generalized real Schur form (S,T), optionally, the left and/or right matrices of Schur vectors (VSL and VSR). This gives the generalized Schur factorization (A,B) = ( (VSL)*S*(VSR)**T, (VSL)*T*(VSR)**T ) Optionally, it also orders the eigenvalues so that a selected cluster of eigenvalues appears in the leading diagonal blocks of the upper quasi-triangular matrix S and the upper triangular matrix T.The leading columns of VSL and VSR then form an orthonormal basis for the corresponding left and right eigenspaces (deflating subspaces). (If only the generalized eigenvalues are needed, use the driver DGGEV instead, which is faster.) A generalized eigenvalue for a pair of matrices (A,B) is a scalar w or a ratio alpha/beta = w, such that A - w*B is singular. It is usually represented as the pair (alpha,beta), as there is a reasonable interpretation for beta=0 or both being zero. A pair of matrices (S,T) is in generalized real Schur form if T is upper triangular with non-negative diagonal and S is block upper triangular with 1-by-1 and 2-by-2 blocks. 1-by-1 blocks correspond to real generalized eigenvalues, while 2-by-2 blocks of S will be "standardized" by making the corresponding elements of T have the form: [ a 0 ] [ 0 b ] and the pair of corresponding 2-by-2 blocks in S and T will have a complex conjugate pair of generalized eigenvalues.
subroutine, public	la_dggesx (jobvsl, jobvsr, sort, selctg, sense, n, a, lda, b, ldb, sdim, alphar, alphai, beta, vsl, ldvsl, vsr, ldvsr, rconde, rcondv, work, lwork, iwork, liwork, bwork, info)
	DGGESX: computes for a pair of N-by-N real nonsymmetric matrices (A,B), the generalized eigenvalues, the real Schur form (S,T), and, optionally, the left and/or right matrices of Schur vectors (VSL and VSR). This gives the generalized Schur factorization (A,B) = ( (VSL) S (VSR)**T, (VSL) T (VSR)**T ) Optionally, it also orders the eigenvalues so that a selected cluster of eigenvalues appears in the leading diagonal blocks of the upper quasi-triangular matrix S and the upper triangular matrix T; computes a reciprocal condition number for the average of the selected eigenvalues (RCONDE); and computes a reciprocal condition number for the right and left deflating subspaces corresponding to the selected eigenvalues (RCONDV). The leading columns of VSL and VSR then form an orthonormal basis for the corresponding left and right eigenspaces (deflating subspaces). A generalized eigenvalue for a pair of matrices (A,B) is a scalar w or a ratio alpha/beta = w, such that A - w*B is singular. It is usually represented as the pair (alpha,beta), as there is a reasonable interpretation for beta=0 or for both being zero. A pair of matrices (S,T) is in generalized real Schur form if T is upper triangular with non-negative diagonal and S is block upper triangular with 1-by-1 and 2-by-2 blocks. 1-by-1 blocks correspond to real generalized eigenvalues, while 2-by-2 blocks of S will be "standardized" by making the corresponding elements of T have the form: [ a 0 ] [ 0 b ] and the pair of corresponding 2-by-2 blocks in S and T will have a complex conjugate pair of generalized eigenvalues.
subroutine, public	la_dggev (jobvl, jobvr, n, a, lda, b, ldb, alphar, alphai, beta, vl, ldvl, vr, ldvr, work, lwork, info)
	DGGEV: computes for a pair of N-by-N real nonsymmetric matrices (A,B) the generalized eigenvalues, and optionally, the left and/or right generalized eigenvectors. A generalized eigenvalue for a pair of matrices (A,B) is a scalar lambda or a ratio alpha/beta = lambda, such that A - lambda*B is singular. It is usually represented as the pair (alpha,beta), as there is a reasonable interpretation for beta=0, and even for both being zero. The right eigenvector v(j) corresponding to the eigenvalue lambda(j) of (A,B) satisfies A * v(j) = lambda(j) * B * v(j). The left eigenvector u(j) corresponding to the eigenvalue lambda(j) of (A,B) satisfies u(j)**H * A = lambda(j) * u(j)**H * B . where u(j)**H is the conjugate-transpose of u(j).
subroutine, public	la_dggevx (balanc, jobvl, jobvr, sense, n, a, lda, b, ldb, alphar, alphai, beta, vl, ldvl, vr, ldvr, ilo, ihi, lscale, rscale, abnrm, bbnrm, rconde, rcondv, work, lwork, iwork, bwork, info)
	DGGEVX: computes for a pair of N-by-N real nonsymmetric matrices (A,B) the generalized eigenvalues, and optionally, the left and/or right generalized eigenvectors. Optionally also, it computes a balancing transformation to improve the conditioning of the eigenvalues and eigenvectors (ILO, IHI, LSCALE, RSCALE, ABNRM, and BBNRM), reciprocal condition numbers for the eigenvalues (RCONDE), and reciprocal condition numbers for the right eigenvectors (RCONDV). A generalized eigenvalue for a pair of matrices (A,B) is a scalar lambda or a ratio alpha/beta = lambda, such that A - lambda*B is singular. It is usually represented as the pair (alpha,beta), as there is a reasonable interpretation for beta=0, and even for both being zero. The right eigenvector v(j) corresponding to the eigenvalue lambda(j) of (A,B) satisfies A * v(j) = lambda(j) * B * v(j) . The left eigenvector u(j) corresponding to the eigenvalue lambda(j) of (A,B) satisfies u(j)**H * A = lambda(j) * u(j)**H * B. where u(j)**H is the conjugate-transpose of u(j).
pure subroutine, public	la_dggglm (n, m, p, a, lda, b, ldb, d, x, y, work, lwork, info)
	DGGGLM: solves a general Gauss-Markov linear model (GLM) problem: minimize || y ||_2 subject to d = A*x + B*y x where A is an N-by-M matrix, B is an N-by-P matrix, and d is a given N-vector. It is assumed that M <= N <= M+P, and rank(A) = M and rank( A B ) = N. Under these assumptions, the constrained equation is always consistent, and there is a unique solution x and a minimal 2-norm solution y, which is obtained using a generalized QR factorization of the matrices (A, B) given by A = Q*(R), B = Q*T*Z. (0) In particular, if matrix B is square nonsingular, then the problem GLM is equivalent to the following weighted linear least squares problem minimize || inv(B)*(d-A*x) ||_2 x where inv(B) denotes the inverse of B.
pure subroutine, public	la_dgglse (m, n, p, a, lda, b, ldb, c, d, x, work, lwork, info)
	DGGLSE: solves the linear equality-constrained least squares (LSE) problem: minimize || c - A*x ||_2 subject to B*x = d where A is an M-by-N matrix, B is a P-by-N matrix, c is a given M-vector, and d is a given P-vector. It is assumed that P <= N <= M+P, and rank(B) = P and rank( (A) ) = N. ( (B) ) These conditions ensure that the LSE problem has a unique solution, which is obtained using a generalized RQ factorization of the matrices (B, A) given by B = (0 R)*Q, A = Z*T*Q.
subroutine, public	la_dhsein (side, eigsrc, initv, select, n, h, ldh, wr, wi, vl, ldvl, vr, ldvr, mm, m, work, ifaill, ifailr, info)
	DHSEIN: uses inverse iteration to find specified right and/or left eigenvectors of a real upper Hessenberg matrix H. The right eigenvector x and the left eigenvector y of the matrix H corresponding to an eigenvalue w are defined by: H * x = w * x, y**h * H = w * y**h where y**h denotes the conjugate transpose of the vector y.
real(dp) function, public	la_dla_porpvgrw (uplo, ncols, a, lda, af, ldaf, work)
	DLA_PORPVGRW: computes the reciprocal pivot growth factor norm(A)/norm(U). The "max absolute element" norm is used. If this is much less than 1, the stability of the LU factorization of the (equilibrated) matrix A could be poor. This also means that the solution X, estimated condition numbers, and error bounds could be unreliable.
pure subroutine, public	la_dlaed3 (k, n, n1, d, q, ldq, rho, dlamda, q2, indx, ctot, w, s, info)
	DLAED3: finds the roots of the secular equation, as defined by the values in D, W, and RHO, between 1 and K. It makes the appropriate calls to DLAED4 and then updates the eigenvectors by multiplying the matrix of eigenvectors of the pair of eigensystems being combined by the matrix of eigenvectors of the K-by-K system which is solved here. This code makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none.
pure subroutine, public	la_dlaed7 (icompq, n, qsiz, tlvls, curlvl, curpbm, d, q, ldq, indxq, rho, cutpnt, qstore, qptr, prmptr, perm, givptr, givcol, givnum, work, iwork, info)
	DLAED7: computes the updated eigensystem of a diagonal matrix after modification by a rank-one symmetric matrix. This routine is used only for the eigenproblem which requires all eigenvalues and optionally eigenvectors of a dense symmetric matrix that has been reduced to tridiagonal form. DLAED1 handles the case in which all eigenvalues and eigenvectors of a symmetric tridiagonal matrix are desired. T = Q(in) ( D(in) + RHO * Z*Z**T ) Q**T(in) = Q(out) * D(out) * Q**T(out) where Z = Q**Tu, u is a vector of length N with ones in the CUTPNT and CUTPNT + 1 th elements and zeros elsewhere. The eigenvectors of the original matrix are stored in Q, and the eigenvalues are in D. The algorithm consists of three stages: The first stage consists of deflating the size of the problem when there are multiple eigenvalues or if there is a zero in the Z vector. For each such occurrence the dimension of the secular equation problem is reduced by one. This stage is performed by the routine DLAED8. The second stage consists of calculating the updated eigenvalues. This is done by finding the roots of the secular equation via the routine DLAED4 (as called by DLAED9). This routine also calculates the eigenvectors of the current problem. The final stage consists of computing the updated eigenvectors directly using the updated eigenvalues. The eigenvectors for the current problem are multiplied with the eigenvectors from the overall problem.
subroutine, public	la_dlaexc (wantq, n, t, ldt, q, ldq, j1, n1, n2, work, info)
	DLAEXC: swaps adjacent diagonal blocks T11 and T22 of order 1 or 2 in an upper quasi-triangular matrix T by an orthogonal similarity transformation. T must be in Schur canonical form, that is, block upper triangular with 1-by-1 and 2-by-2 diagonal blocks; each 2-by-2 diagonal block has its diagonal elements equal and its off-diagonal elements of opposite sign.
pure subroutine, public	la_dlahqr (wantt, wantz, n, ilo, ihi, h, ldh, wr, wi, iloz, ihiz, z, ldz, info)
	DLAHQR: is an auxiliary routine called by DHSEQR to update the eigenvalues and Schur decomposition already computed by DHSEQR, by dealing with the Hessenberg submatrix in rows and columns ILO to IHI.
pure subroutine, public	la_dlasd2 (nl, nr, sqre, k, d, z, alpha, beta, u, ldu, vt, ldvt, dsigma, u2, ldu2, vt2, ldvt2, idxp, idx, idxc, idxq, coltyp, info)
	DLASD2: merges the two sets of singular values together into a single sorted set. Then it tries to deflate the size of the problem. There are two ways in which deflation can occur: when two or more singular values are close together or if there is a tiny entry in the Z vector. For each such occurrence the order of the related secular equation problem is reduced by one. DLASD2 is called from DLASD1.
pure subroutine, public	la_dlaswlq (m, n, mb, nb, a, lda, t, ldt, work, lwork, info)
	DLASWLQ: computes a blocked Tall-Skinny LQ factorization of a real M-by-N matrix A for M <= N: A = ( L 0 ) * Q, where: Q is a n-by-N orthogonal matrix, stored on exit in an implicit form in the elements above the diagonal of the array A and in the elements of the array T; L is a lower-triangular M-by-M matrix stored on exit in the elements on and below the diagonal of the array A. 0 is a M-by-(N-M) zero matrix, if M < N, and is not stored.
pure subroutine, public	la_dlatsqr (m, n, mb, nb, a, lda, t, ldt, work, lwork, info)
	DLATSQR: computes a blocked Tall-Skinny QR factorization of a real M-by-N matrix A for M >= N: A = Q * ( R ), ( 0 ) where: Q is a M-by-M orthogonal matrix, stored on exit in an implicit form in the elements below the diagonal of the array A and in the elements of the array T; R is an upper-triangular N-by-N matrix, stored on exit in the elements on and above the diagonal of the array A. 0 is a (M-N)-by-N zero matrix, and is not stored.
pure subroutine, public	la_dorgbr (vect, m, n, k, a, lda, tau, work, lwork, info)
	DORGBR: generates one of the real orthogonal matrices Q or P**T determined by DGEBRD when reducing a real matrix A to bidiagonal form: A = Q * B * P**T. Q and P**T are defined as products of elementary reflectors H(i) or G(i) respectively. If VECT = 'Q', A is assumed to have been an M-by-K matrix, and Q is of order M: if m >= k, Q = H(1) H(2) . . . H(k) and DORGBR returns the first n columns of Q, where m >= n >= k; if m < k, Q = H(1) H(2) . . . H(m-1) and DORGBR returns Q as an M-by-M matrix. If VECT = 'P', A is assumed to have been a K-by-N matrix, and P**T is of order N: if k < n, P**T = G(k) . . . G(2) G(1) and DORGBR returns the first m rows of P**T, where n >= m >= k; if k >= n, P**T = G(n-1) . . . G(2) G(1) and DORGBR returns P**T as an N-by-N matrix.
pure subroutine, public	la_dormbr (vect, side, trans, m, n, k, a, lda, tau, c, ldc, work, lwork, info)
	If VECT = 'Q', DORMBR: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q * C C * Q TRANS = 'T': Q**T * C C * Q**T If VECT = 'P', DORMBR overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': P * C C * P TRANS = 'T': P**T * C C * P**T Here Q and P**T are the orthogonal matrices determined by DGEBRD when reducing a real matrix A to bidiagonal form: A = Q * B * P**T. Q and P**T are defined as products of elementary reflectors H(i) and G(i) respectively. Let nq = m if SIDE = 'L' and nq = n if SIDE = 'R'. Thus nq is the order of the orthogonal matrix Q or P**T that is applied. If VECT = 'Q', A is assumed to have been an NQ-by-K matrix: if nq >= k, Q = H(1) H(2) . . . H(k); if nq < k, Q = H(1) H(2) . . . H(nq-1). If VECT = 'P', A is assumed to have been a K-by-NQ matrix: if k < nq, P = G(1) G(2) . . . G(k); if k >= nq, P = G(1) G(2) . . . G(nq-1).
pure subroutine, public	la_dpbsv (uplo, n, kd, nrhs, ab, ldab, b, ldb, info)
	DPBSV: computes the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric positive definite band matrix and X and B are N-by-NRHS matrices. The Cholesky decomposition is used to factor A as A = U**T * U, if UPLO = 'U', or A = L * L**T, if UPLO = 'L', where U is an upper triangular band matrix, and L is a lower triangular band matrix, with the same number of superdiagonals or subdiagonals as A. The factored form of A is then used to solve the system of equations A * X = B.
subroutine, public	la_dpbsvx (fact, uplo, n, kd, nrhs, ab, ldab, afb, ldafb, equed, s, b, ldb, x, ldx, rcond, ferr, berr, work, iwork, info)
	DPBSVX: uses the Cholesky factorization A = U**T*U or A = L*L**T to compute the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric positive definite band matrix and X and B are N-by-NRHS matrices. Error bounds on the solution and a condition estimate are also provided.
pure subroutine, public	la_dpftrf (transr, uplo, n, a, info)
	DPFTRF: computes the Cholesky factorization of a real symmetric positive definite matrix A. The factorization has the form A = U**T * U, if UPLO = 'U', or A = L * L**T, if UPLO = 'L', where U is an upper triangular matrix and L is lower triangular. This is the block version of the algorithm, calling Level 3 BLAS.
pure subroutine, public	la_dposv (uplo, n, nrhs, a, lda, b, ldb, info)
	DPOSV: computes the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric positive definite matrix and X and B are N-by-NRHS matrices. The Cholesky decomposition is used to factor A as A = U**T* U, if UPLO = 'U', or A = L * L**T, if UPLO = 'L', where U is an upper triangular matrix and L is a lower triangular matrix. The factored form of A is then used to solve the system of equations A * X = B.
subroutine, public	la_dposvx (fact, uplo, n, nrhs, a, lda, af, ldaf, equed, s, b, ldb, x, ldx, rcond, ferr, berr, work, iwork, info)
	DPOSVX: uses the Cholesky factorization A = U**T*U or A = L*L**T to compute the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric positive definite matrix and X and B are N-by-NRHS matrices. Error bounds on the solution and a condition estimate are also provided.
subroutine, public	la_dtrexc (compq, n, t, ldt, q, ldq, ifst, ilst, work, info)
	DTREXC: reorders the real Schur factorization of a real matrix A = Q*T*Q**T, so that the diagonal block of T with row index IFST is moved to row ILST. The real Schur form T is reordered by an orthogonal similarity transformation Z**T*T*Z, and optionally the matrix Q of Schur vectors is updated by postmultiplying it with Z. T must be in Schur canonical form (as returned by DHSEQR), that is, block upper triangular with 1-by-1 and 2-by-2 diagonal blocks; each 2-by-2 diagonal block has its diagonal elements equal and its off-diagonal elements of opposite sign.
subroutine, public	la_dtrsen (job, compq, select, n, t, ldt, q, ldq, wr, wi, m, s, sep, work, lwork, iwork, liwork, info)
	DTRSEN: reorders the real Schur factorization of a real matrix A = Q*T*Q**T, so that a selected cluster of eigenvalues appears in the leading diagonal blocks of the upper quasi-triangular matrix T, and the leading columns of Q form an orthonormal basis of the corresponding right invariant subspace. Optionally the routine computes the reciprocal condition numbers of the cluster of eigenvalues and/or the invariant subspace. T must be in Schur canonical form (as returned by DHSEQR), that is, block upper triangular with 1-by-1 and 2-by-2 diagonal blocks; each 2-by-2 diagonal block has its diagonal elements equal and its off-diagonal elements of opposite sign.
subroutine, public	la_dtrsna (job, howmny, select, n, t, ldt, vl, ldvl, vr, ldvr, s, sep, mm, m, work, ldwork, iwork, info)
	DTRSNA: estimates reciprocal condition numbers for specified eigenvalues and/or right eigenvectors of a real upper quasi-triangular matrix T (or of any matrix Q*T*Q**T with Q orthogonal). T must be in Schur canonical form (as returned by DHSEQR), that is, block upper triangular with 1-by-1 and 2-by-2 diagonal blocks; each 2-by-2 diagonal block has its diagonal elements equal and its off-diagonal elements of opposite sign.
pure subroutine, public	la_dgejsv (joba, jobu, jobv, jobr, jobt, jobp, m, n, a, lda, sva, u, ldu, v, ldv, work, lwork, iwork, info)
	DGEJSV: computes the singular value decomposition (SVD) of a real M-by-N matrix [A], where M >= N. The SVD of [A] is written as [A] = [U] * [SIGMA] * [V]^t, where [SIGMA] is an N-by-N (M-by-N) matrix which is zero except for its N diagonal elements, [U] is an M-by-N (or M-by-M) orthonormal matrix, and [V] is an N-by-N orthogonal matrix. The diagonal elements of [SIGMA] are the singular values of [A]. The columns of [U] and [V] are the left and the right singular vectors of [A], respectively. The matrices [U] and [V] are computed and stored in the arrays U and V, respectively. The diagonal of [SIGMA] is computed and stored in the array SVA. DGEJSV can sometimes compute tiny singular values and their singular vectors much more accurately than other SVD routines, see below under Further Details.
pure subroutine, public	la_dgelq (m, n, a, lda, t, tsize, work, lwork, info)
	DGELQ: computes an LQ factorization of a real M-by-N matrix A: A = ( L 0 ) * Q where: Q is a N-by-N orthogonal matrix; L is a lower-triangular M-by-M matrix; 0 is a M-by-(N-M) zero matrix, if M < N.
subroutine, public	la_dgelsy (m, n, nrhs, a, lda, b, ldb, jpvt, rcond, rank, work, lwork, info)
	DGELSY: computes the minimum-norm solution to a real linear least squares problem: minimize || A * X - B || using a complete orthogonal factorization of A. A is an M-by-N matrix which may be rank-deficient. Several right hand side vectors b and solution vectors x can be handled in a single call; they are stored as the columns of the M-by-NRHS right hand side matrix B and the N-by-NRHS solution matrix X. The routine first computes a QR factorization with column pivoting: A * P = Q * [ R11 R12 ] [ 0 R22 ] with R11 defined as the largest leading submatrix whose estimated condition number is less than 1/RCOND. The order of R11, RANK, is the effective rank of A. Then, R22 is considered to be negligible, and R12 is annihilated by orthogonal transformations from the right, arriving at the complete orthogonal factorization: A * P = Q * [ T11 0 ] * Z [ 0 0 ] The minimum-norm solution is then X = P * Z**T [ inv(T11)*Q1**T*B ] [ 0 ] where Q1 consists of the first RANK columns of Q. This routine is basically identical to the original xGELSX except three differences: o The call to the subroutine xGEQPF has been substituted by the the call to the subroutine xGEQP3. This subroutine is a Blas-3 version of the QR factorization with column pivoting. o Matrix B (the right hand side) is updated with Blas-3. o The permutation of matrix B (the right hand side) is faster and more simple.
pure subroutine, public	la_dgeqr (m, n, a, lda, t, tsize, work, lwork, info)
	DGEQR: computes a QR factorization of a real M-by-N matrix A: A = Q * ( R ), ( 0 ) where: Q is a M-by-M orthogonal matrix; R is an upper-triangular N-by-N matrix; 0 is a (M-N)-by-N zero matrix, if M > N.
subroutine, public	la_dgetsls (trans, m, n, nrhs, a, lda, b, ldb, work, lwork, info)
	DGETSLS: solves overdetermined or underdetermined real linear systems involving an M-by-N matrix A, using a tall skinny QR or short wide LQ factorization of A. It is assumed that A has full rank. The following options are provided:
pure subroutine, public	la_dgetsqrhrt (m, n, mb1, nb1, nb2, a, lda, t, ldt, work, lwork, info)
	DGETSQRHRT: computes a NB2-sized column blocked QR-factorization of a real M-by-N matrix A with M >= N, A = Q * R. The routine uses internally a NB1-sized column blocked and MB1-sized row blocked TSQR-factorization and perfors the reconstruction of the Householder vectors from the TSQR output. The routine also converts the R_tsqr factor from the TSQR-factorization output into the R factor that corresponds to the Householder QR-factorization, A = Q_tsqr * R_tsqr = Q * R. The output Q and R factors are stored in the same format as in DGEQRT (Q is in blocked compact WY-representation). See the documentation of DGEQRT for more details on the format.
pure subroutine, public	la_dlaed2 (k, n, n1, d, q, ldq, indxq, rho, z, dlamda, w, q2, indx, indxc, indxp, coltyp, info)
	DLAED2: merges the two sets of eigenvalues together into a single sorted set. Then it tries to deflate the size of the problem. There are two ways in which deflation can occur: when two or more eigenvalues are close together or if there is a tiny entry in the Z vector. For each such occurrence the order of the related secular equation problem is reduced by one.
subroutine, public	la_dlaqr2 (wantt, wantz, n, ktop, kbot, nw, h, ldh, iloz, ihiz, z, ldz, ns, nd, sr, si, v, ldv, nh, t, ldt, nv, wv, ldwv, work, lwork)
	DLAQR2: is identical to DLAQR3 except that it avoids recursion by calling DLAHQR instead of DLAQR4. Aggressive early deflation: This subroutine accepts as input an upper Hessenberg matrix H and performs an orthogonal similarity transformation designed to detect and deflate fully converged eigenvalues from a trailing principal submatrix. On output H has been over- written by a new Hessenberg matrix that is a perturbation of an orthogonal similarity transformation of H. It is to be hoped that the final version of H has many zero subdiagonal entries.
pure subroutine, public	la_dlasd1 (nl, nr, sqre, d, alpha, beta, u, ldu, vt, ldvt, idxq, iwork, work, info)
	DLASD1: computes the SVD of an upper bidiagonal N-by-M matrix B, where N = NL + NR + 1 and M = N + SQRE. DLASD1 is called from DLASD0. A related subroutine DLASD7 handles the case in which the singular values (and the singular vectors in factored form) are desired. DLASD1 computes the SVD as follows: ( D1(in) 0 0 0 ) B = U(in) * ( Z1**T a Z2**T b ) * VT(in) ( 0 0 D2(in) 0 ) = U(out) * ( D(out) 0) * VT(out) where Z**T = (Z1**T a Z2**T b) = u**T VT**T, and u is a vector of dimension M with ALPHA and BETA in the NL+1 and NL+2 th entries and zeros elsewhere; and the entry b is empty if SQRE = 0. The left singular vectors of the original matrix are stored in U, and the transpose of the right singular vectors are stored in VT, and the singular values are in D. The algorithm consists of three stages: The first stage consists of deflating the size of the problem when there are multiple singular values or when there are zeros in the Z vector. For each such occurrence the dimension of the secular equation problem is reduced by one. This stage is performed by the routine DLASD2. The second stage consists of calculating the updated singular values. This is done by finding the square roots of the roots of the secular equation via the routine DLASD4 (as called by DLASD3). This routine also calculates the singular vectors of the current problem. The final stage consists of computing the updated singular vectors directly using the updated singular values. The singular vectors for the current problem are multiplied with the singular vectors from the overall problem.
pure subroutine, public	la_dlaed1 (n, d, q, ldq, indxq, rho, cutpnt, work, iwork, info)
	DLAED1: computes the updated eigensystem of a diagonal matrix after modification by a rank-one symmetric matrix. This routine is used only for the eigenproblem which requires all eigenvalues and eigenvectors of a tridiagonal matrix. DLAED7 handles the case in which eigenvalues only or eigenvalues and eigenvectors of a full symmetric matrix (which was reduced to tridiagonal form) are desired. T = Q(in) ( D(in) + RHO * Z*Z**T ) Q**T(in) = Q(out) * D(out) * Q**T(out) where Z = Q**T*u, u is a vector of length N with ones in the CUTPNT and CUTPNT + 1 th elements and zeros elsewhere. The eigenvectors of the original matrix are stored in Q, and the eigenvalues are in D. The algorithm consists of three stages: The first stage consists of deflating the size of the problem when there are multiple eigenvalues or if there is a zero in the Z vector. For each such occurrence the dimension of the secular equation problem is reduced by one. This stage is performed by the routine DLAED2. The second stage consists of calculating the updated eigenvalues. This is done by finding the roots of the secular equation via the routine DLAED4 (as called by DLAED3). This routine also calculates the eigenvectors of the current problem. The final stage consists of computing the updated eigenvectors directly using the updated eigenvalues. The eigenvectors for the current problem are multiplied with the eigenvectors from the overall problem.
pure subroutine, public	la_dlaed0 (icompq, qsiz, n, d, e, q, ldq, qstore, ldqs, work, iwork, info)
	DLAED0: computes all eigenvalues and corresponding eigenvectors of a symmetric tridiagonal matrix using the divide and conquer method.
pure subroutine, public	la_dstedc (compz, n, d, e, z, ldz, work, lwork, iwork, liwork, info)
	DSTEDC: computes all eigenvalues and, optionally, eigenvectors of a symmetric tridiagonal matrix using the divide and conquer method. The eigenvectors of a full or band real symmetric matrix can also be found if DSYTRD or DSPTRD or DSBTRD has been used to reduce this matrix to tridiagonal form. This code makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none. See DLAED3 for details.
pure subroutine, public	la_dstevd (jobz, n, d, e, z, ldz, work, lwork, iwork, liwork, info)
	DSTEVD: computes all eigenvalues and, optionally, eigenvectors of a real symmetric tridiagonal matrix. If eigenvectors are desired, it uses a divide and conquer algorithm. The divide and conquer algorithm makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none.
subroutine, public	la_dsyevd (jobz, uplo, n, a, lda, w, work, lwork, iwork, liwork, info)
	DSYEVD: computes all eigenvalues and, optionally, eigenvectors of a real symmetric matrix A. If eigenvectors are desired, it uses a divide and conquer algorithm. The divide and conquer algorithm makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none. Because of large use of BLAS of level 3, DSYEVD needs N**2 more workspace than DSYEVX.
subroutine, public	la_dsygvd (itype, jobz, uplo, n, a, lda, b, ldb, w, work, lwork, iwork, liwork, info)
	DSYGVD: computes all the eigenvalues, and optionally, the eigenvectors of a real generalized symmetric-definite eigenproblem, of the form A*x=(lambda)*B*x, A*Bx=(lambda)*x, or B*A*x=(lambda)*x. Here A and B are assumed to be symmetric and B is also positive definite. If eigenvectors are desired, it uses a divide and conquer algorithm. The divide and conquer algorithm makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none.
subroutine, public	la_dsbevd (jobz, uplo, n, kd, ab, ldab, w, z, ldz, work, lwork, iwork, liwork, info)
	DSBEVD: computes all the eigenvalues and, optionally, eigenvectors of a real symmetric band matrix A. If eigenvectors are desired, it uses a divide and conquer algorithm. The divide and conquer algorithm makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none.
pure subroutine, public	la_dsbgvd (jobz, uplo, n, ka, kb, ab, ldab, bb, ldbb, w, z, ldz, work, lwork, iwork, liwork, info)
	DSBGVD: computes all the eigenvalues, and optionally, the eigenvectors of a real generalized symmetric-definite banded eigenproblem, of the form A*x=(lambda)*B*x. Here A and B are assumed to be symmetric and banded, and B is also positive definite. If eigenvectors are desired, it uses a divide and conquer algorithm. The divide and conquer algorithm makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none.
subroutine, public	la_dspevd (jobz, uplo, n, ap, w, z, ldz, work, lwork, iwork, liwork, info)
	DSPEVD: computes all the eigenvalues and, optionally, eigenvectors of a real symmetric matrix A in packed storage. If eigenvectors are desired, it uses a divide and conquer algorithm. The divide and conquer algorithm makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none.
subroutine, public	la_dspgvd (itype, jobz, uplo, n, ap, bp, w, z, ldz, work, lwork, iwork, liwork, info)
	DSPGVD: computes all the eigenvalues, and optionally, the eigenvectors of a real generalized symmetric-definite eigenproblem, of the form A*x=(lambda)*B*x, A*Bx=(lambda)*x, or B*A*x=(lambda)*x. Here A and B are assumed to be symmetric, stored in packed format, and B is also positive definite. If eigenvectors are desired, it uses a divide and conquer algorithm. The divide and conquer algorithm makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none.
pure subroutine, public	la_dbdsdc (uplo, compq, n, d, e, u, ldu, vt, ldvt, q, iq, work, iwork, info)
	DBDSDC: computes the singular value decomposition (SVD) of a real N-by-N (upper or lower) bidiagonal matrix B: B = U * S * VT, using a divide and conquer method, where S is a diagonal matrix with non-negative diagonal elements (the singular values of B), and U and VT are orthogonal matrices of left and right singular vectors, respectively. DBDSDC can be used to compute all singular values, and optionally, singular vectors or singular vectors in compact form. This code makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none. See DLASD3 for details. The code currently calls DLASDQ if singular values only are desired. However, it can be slightly modified to compute singular values using the divide and conquer method.
pure subroutine, public	la_dbdsqr (uplo, n, ncvt, nru, ncc, d, e, vt, ldvt, u, ldu, c, ldc, work, info)
	DBDSQR: computes the singular values and, optionally, the right and/or left singular vectors from the singular value decomposition (SVD) of a real N-by-N (upper or lower) bidiagonal matrix B using the implicit zero-shift QR algorithm. The SVD of B has the form B = Q * S * P**T where S is the diagonal matrix of singular values, Q is an orthogonal matrix of left singular vectors, and P is an orthogonal matrix of right singular vectors. If left singular vectors are requested, this subroutine actually returns U*Q instead of Q, and, if right singular vectors are requested, this subroutine returns P**T*VT instead of P**T, for given real input matrices U and VT. When U and VT are the orthogonal matrices that reduce a general matrix A to bidiagonal form: A = U*B*VT, as computed by DGEBRD, then A = (U*Q) * S * (P**T*VT) is the SVD of A. Optionally, the subroutine may also compute Q**T*C for a given real input matrix C. See "Computing Small Singular Values of Bidiagonal Matrices With Guaranteed High Relative Accuracy," by J. Demmel and W. Kahan, LAPACK Working Note #3 (or SIAM J. Sci. Statist. Comput. vol. 11, no. 5, pp. 873-912, Sept 1990) and "Accurate singular values and differential qd algorithms," by B. Parlett and V. Fernando, Technical Report CPAM-554, Mathematics Department, University of California at Berkeley, July 1992 for a detailed description of the algorithm.
subroutine, public	la_dgees (jobvs, sort, select, n, a, lda, sdim, wr, wi, vs, ldvs, work, lwork, bwork, info)
	DGEES: computes for an N-by-N real nonsymmetric matrix A, the eigenvalues, the real Schur form T, and, optionally, the matrix of Schur vectors Z. This gives the Schur factorization A = Z*T*(Z**T). Optionally, it also orders the eigenvalues on the diagonal of the real Schur form so that selected eigenvalues are at the top left. The leading columns of Z then form an orthonormal basis for the invariant subspace corresponding to the selected eigenvalues. A matrix is in real Schur form if it is upper quasi-triangular with 1-by-1 and 2-by-2 blocks. 2-by-2 blocks will be standardized in the form [ a b ] [ c a ] where b*c < 0. The eigenvalues of such a block are a +- sqrt(bc).
subroutine, public	la_dgeesx (jobvs, sort, select, sense, n, a, lda, sdim, wr, wi, vs, ldvs, rconde, rcondv, work, lwork, iwork, liwork, bwork, info)
	DGEESX: computes for an N-by-N real nonsymmetric matrix A, the eigenvalues, the real Schur form T, and, optionally, the matrix of Schur vectors Z. This gives the Schur factorization A = Z*T*(Z**T). Optionally, it also orders the eigenvalues on the diagonal of the real Schur form so that selected eigenvalues are at the top left; computes a reciprocal condition number for the average of the selected eigenvalues (RCONDE); and computes a reciprocal condition number for the right invariant subspace corresponding to the selected eigenvalues (RCONDV). The leading columns of Z form an orthonormal basis for this invariant subspace. For further explanation of the reciprocal condition numbers RCONDE and RCONDV, see Section 4.10_dp of the LAPACK Users' Guide (where these quantities are called s and sep respectively). A real matrix is in real Schur form if it is upper quasi-triangular with 1-by-1 and 2-by-2 blocks. 2-by-2 blocks will be standardized in the form [ a b ] [ c a ] where b*c < 0. The eigenvalues of such a block are a +- sqrt(bc).
subroutine, public	la_dgeev (jobvl, jobvr, n, a, lda, wr, wi, vl, ldvl, vr, ldvr, work, lwork, info)
	DGEEV: computes for an N-by-N real nonsymmetric matrix A, the eigenvalues and, optionally, the left and/or right eigenvectors. The right eigenvector v(j) of A satisfies A * v(j) = lambda(j) * v(j) where lambda(j) is its eigenvalue. The left eigenvector u(j) of A satisfies u(j)**H * A = lambda(j) * u(j)**H where u(j)**H denotes the conjugate-transpose of u(j). The computed eigenvectors are normalized to have Euclidean norm equal to 1 and largest component real.
subroutine, public	la_dgeevx (balanc, jobvl, jobvr, sense, n, a, lda, wr, wi, vl, ldvl, vr, ldvr, ilo, ihi, scale, abnrm, rconde, rcondv, work, lwork, iwork, info)
	DGEEVX: computes for an N-by-N real nonsymmetric matrix A, the eigenvalues and, optionally, the left and/or right eigenvectors. Optionally also, it computes a balancing transformation to improve the conditioning of the eigenvalues and eigenvectors (ILO, IHI, SCALE, and ABNRM), reciprocal condition numbers for the eigenvalues (RCONDE), and reciprocal condition numbers for the right eigenvectors (RCONDV). The right eigenvector v(j) of A satisfies A * v(j) = lambda(j) * v(j) where lambda(j) is its eigenvalue. The left eigenvector u(j) of A satisfies u(j)**H * A = lambda(j) * u(j)**H where u(j)**H denotes the conjugate-transpose of u(j). The computed eigenvectors are normalized to have Euclidean norm equal to 1 and largest component real. Balancing a matrix means permuting the rows and columns to make it more nearly upper triangular, and applying a diagonal similarity transformation D * A * D**(-1), where D is a diagonal matrix, to make its rows and columns closer in norm and the condition numbers of its eigenvalues and eigenvectors smaller. The computed reciprocal condition numbers correspond to the balanced matrix. Permuting rows and columns will not change the condition numbers (in exact arithmetic) but diagonal scaling will. For further explanation of balancing, see section 4.10.2_dp of the LAPACK Users' Guide.
subroutine, public	la_dgelsd (m, n, nrhs, a, lda, b, ldb, s, rcond, rank, work, lwork, iwork, info)
	DGELSD: computes the minimum-norm solution to a real linear least squares problem: minimize 2-norm(| b - A*x |) using the singular value decomposition (SVD) of A. A is an M-by-N matrix which may be rank-deficient. Several right hand side vectors b and solution vectors x can be handled in a single call; they are stored as the columns of the M-by-NRHS right hand side matrix B and the N-by-NRHS solution matrix X. The problem is solved in three steps: (1) Reduce the coefficient matrix A to bidiagonal form with Householder transformations, reducing the original problem into a "bidiagonal least squares problem" (BLS) (2) Solve the BLS using a divide and conquer approach. (3) Apply back all the Householder transformations to solve the original least squares problem. The effective rank of A is determined by treating as zero those singular values which are less than RCOND times the largest singular value. The divide and conquer algorithm makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none.
subroutine, public	la_dgelss (m, n, nrhs, a, lda, b, ldb, s, rcond, rank, work, lwork, info)
	DGELSS: computes the minimum norm solution to a real linear least squares problem: Minimize 2-norm(| b - A*x |). using the singular value decomposition (SVD) of A. A is an M-by-N matrix which may be rank-deficient. Several right hand side vectors b and solution vectors x can be handled in a single call; they are stored as the columns of the M-by-NRHS right hand side matrix B and the N-by-NRHS solution matrix X. The effective rank of A is determined by treating as zero those singular values which are less than RCOND times the largest singular value.
subroutine, public	la_dgesdd (jobz, m, n, a, lda, s, u, ldu, vt, ldvt, work, lwork, iwork, info)
	DGESDD: computes the singular value decomposition (SVD) of a real M-by-N matrix A, optionally computing the left and right singular vectors. If singular vectors are desired, it uses a divide-and-conquer algorithm. The SVD is written A = U * SIGMA * transpose(V) where SIGMA is an M-by-N matrix which is zero except for its min(m,n) diagonal elements, U is an M-by-M orthogonal matrix, and V is an N-by-N orthogonal matrix. The diagonal elements of SIGMA are the singular values of A; they are real and non-negative, and are returned in descending order. The first min(m,n) columns of U and V are the left and right singular vectors of A. Note that the routine returns VT = V**T, not V. The divide and conquer algorithm makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none.
subroutine, public	la_dgesvd (jobu, jobvt, m, n, a, lda, s, u, ldu, vt, ldvt, work, lwork, info)
	DGESVD: computes the singular value decomposition (SVD) of a real M-by-N matrix A, optionally computing the left and/or right singular vectors. The SVD is written A = U * SIGMA * transpose(V) where SIGMA is an M-by-N matrix which is zero except for its min(m,n) diagonal elements, U is an M-by-M orthogonal matrix, and V is an N-by-N orthogonal matrix. The diagonal elements of SIGMA are the singular values of A; they are real and non-negative, and are returned in descending order. The first min(m,n) columns of U and V are the left and right singular vectors of A. Note that the routine returns V**T, not V.
subroutine, public	la_dgesvdq (joba, jobp, jobr, jobu, jobv, m, n, a, lda, s, u, ldu, v, ldv, numrank, iwork, liwork, work, lwork, rwork, lrwork, info)
	DGESVDQ: computes the singular value decomposition (SVD) of a real M-by-N matrix A, where M >= N. The SVD of A is written as [++] [xx] [x0] [xx] A = U * SIGMA * V^*, [++] = [xx] * [ox] * [xx] [++] [xx] where SIGMA is an N-by-N diagonal matrix, U is an M-by-N orthonormal matrix, and V is an N-by-N orthogonal matrix. The diagonal elements of SIGMA are the singular values of A. The columns of U and V are the left and the right singular vectors of A, respectively.
subroutine, public	la_dgges3 (jobvsl, jobvsr, sort, selctg, n, a, lda, b, ldb, sdim, alphar, alphai, beta, vsl, ldvsl, vsr, ldvsr, work, lwork, bwork, info)
	DGGES3: computes for a pair of N-by-N real nonsymmetric matrices (A,B), the generalized eigenvalues, the generalized real Schur form (S,T), optionally, the left and/or right matrices of Schur vectors (VSL and VSR). This gives the generalized Schur factorization (A,B) = ( (VSL)*S*(VSR)**T, (VSL)*T*(VSR)**T ) Optionally, it also orders the eigenvalues so that a selected cluster of eigenvalues appears in the leading diagonal blocks of the upper quasi-triangular matrix S and the upper triangular matrix T.The leading columns of VSL and VSR then form an orthonormal basis for the corresponding left and right eigenspaces (deflating subspaces). (If only the generalized eigenvalues are needed, use the driver DGGEV instead, which is faster.) A generalized eigenvalue for a pair of matrices (A,B) is a scalar w or a ratio alpha/beta = w, such that A - w*B is singular. It is usually represented as the pair (alpha,beta), as there is a reasonable interpretation for beta=0 or both being zero. A pair of matrices (S,T) is in generalized real Schur form if T is upper triangular with non-negative diagonal and S is block upper triangular with 1-by-1 and 2-by-2 blocks. 1-by-1 blocks correspond to real generalized eigenvalues, while 2-by-2 blocks of S will be "standardized" by making the corresponding elements of T have the form: [ a 0 ] [ 0 b ] and the pair of corresponding 2-by-2 blocks in S and T will have a complex conjugate pair of generalized eigenvalues.
subroutine, public	la_dggev3 (jobvl, jobvr, n, a, lda, b, ldb, alphar, alphai, beta, vl, ldvl, vr, ldvr, work, lwork, info)
	DGGEV3: computes for a pair of N-by-N real nonsymmetric matrices (A,B) the generalized eigenvalues, and optionally, the left and/or right generalized eigenvectors. A generalized eigenvalue for a pair of matrices (A,B) is a scalar lambda or a ratio alpha/beta = lambda, such that A - lambda*B is singular. It is usually represented as the pair (alpha,beta), as there is a reasonable interpretation for beta=0, and even for both being zero. The right eigenvector v(j) corresponding to the eigenvalue lambda(j) of (A,B) satisfies A * v(j) = lambda(j) * B * v(j). The left eigenvector u(j) corresponding to the eigenvalue lambda(j) of (A,B) satisfies u(j)**H * A = lambda(j) * u(j)**H * B . where u(j)**H is the conjugate-transpose of u(j).
subroutine, public	la_dhseqr (job, compz, n, ilo, ihi, h, ldh, wr, wi, z, ldz, work, lwork, info)
	DHSEQR: computes the eigenvalues of a Hessenberg matrix H and, optionally, the matrices T and Z from the Schur decomposition H = Z T Z**T, where T is an upper quasi-triangular matrix (the Schur form), and Z is the orthogonal matrix of Schur vectors. Optionally Z may be postmultiplied into an input orthogonal matrix Q so that this routine can give the Schur factorization of a matrix A which has been reduced to the Hessenberg form H by the orthogonal matrix Q: A = Q*H*Q**T = (QZ)*T*(QZ)**T.
pure subroutine, public	la_dlalsa (icompq, smlsiz, n, nrhs, b, ldb, bx, ldbx, u, ldu, vt, k, difl, difr, z, poles, givptr, givcol, ldgcol, perm, givnum, c, s, work, iwork, info)
	DLALSA: is an itermediate step in solving the least squares problem by computing the SVD of the coefficient matrix in compact form (The singular vectors are computed as products of simple orthorgonal matrices.). If ICOMPQ = 0, DLALSA applies the inverse of the left singular vector matrix of an upper bidiagonal matrix to the right hand side; and if ICOMPQ = 1, DLALSA applies the right singular vector matrix to the right hand side. The singular vector matrices were generated in compact form by DLALSA.
pure subroutine, public	la_dlalsd (uplo, smlsiz, n, nrhs, d, e, b, ldb, rcond, rank, work, iwork, info)
	DLALSD: uses the singular value decomposition of A to solve the least squares problem of finding X to minimize the Euclidean norm of each column of A*X-B, where A is N-by-N upper bidiagonal, and X and B are N-by-NRHS. The solution X overwrites B. The singular values of A smaller than RCOND times the largest singular value are treated as zero in solving the least squares problem; in this case a minimum norm solution is returned. The actual singular values are returned in D in ascending order. This code makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray XMP, Cray YMP, Cray C 90, or Cray 2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none.
subroutine, public	la_dlaqr0 (wantt, wantz, n, ilo, ihi, h, ldh, wr, wi, iloz, ihiz, z, ldz, work, lwork, info)
	DLAQR0: computes the eigenvalues of a Hessenberg matrix H and, optionally, the matrices T and Z from the Schur decomposition H = Z T Z**T, where T is an upper quasi-triangular matrix (the Schur form), and Z is the orthogonal matrix of Schur vectors. Optionally Z may be postmultiplied into an input orthogonal matrix Q so that this routine can give the Schur factorization of a matrix A which has been reduced to the Hessenberg form H by the orthogonal matrix Q: A = Q*H*Q**T = (QZ)*T*(QZ)**T.
subroutine, public	la_dlaqr3 (wantt, wantz, n, ktop, kbot, nw, h, ldh, iloz, ihiz, z, ldz, ns, nd, sr, si, v, ldv, nh, t, ldt, nv, wv, ldwv, work, lwork)
	Aggressive early deflation: DLAQR3: accepts as input an upper Hessenberg matrix H and performs an orthogonal similarity transformation designed to detect and deflate fully converged eigenvalues from a trailing principal submatrix. On output H has been over- written by a new Hessenberg matrix that is a perturbation of an orthogonal similarity transformation of H. It is to be hoped that the final version of H has many zero subdiagonal entries.
subroutine, public	la_dlaqr4 (wantt, wantz, n, ilo, ihi, h, ldh, wr, wi, iloz, ihiz, z, ldz, work, lwork, info)
	DLAQR4: implements one level of recursion for DLAQR0. It is a complete implementation of the small bulge multi-shift QR algorithm. It may be called by DLAQR0 and, for large enough deflation window size, it may be called by DLAQR3. This subroutine is identical to DLAQR0 except that it calls DLAQR2 instead of DLAQR3. DLAQR4 computes the eigenvalues of a Hessenberg matrix H and, optionally, the matrices T and Z from the Schur decomposition H = Z T Z**T, where T is an upper quasi-triangular matrix (the Schur form), and Z is the orthogonal matrix of Schur vectors. Optionally Z may be postmultiplied into an input orthogonal matrix Q so that this routine can give the Schur factorization of a matrix A which has been reduced to the Hessenberg form H by the orthogonal matrix Q: A = Q*H*Q**T = (QZ)*T*(QZ)**T.
recursive subroutine, public	la_dlaqz0 (wants, wantq, wantz, n, ilo, ihi, a, lda, b, ldb, alphar, alphai, beta, q, ldq, z, ldz, work, lwork, rec, info)
	DLAQZ0: computes the eigenvalues of a real matrix pair (H,T), where H is an upper Hessenberg matrix and T is upper triangular, using the double-shift QZ method. Matrix pairs of this type are produced by the reduction to generalized upper Hessenberg form of a real matrix pair (A,B): A = Q1*H*Z1**T, B = Q1*T*Z1**T, as computed by DGGHRD. If JOB='S', then the Hessenberg-triangular pair (H,T) is also reduced to generalized Schur form, H = Q*S*Z**T, T = Q*P*Z**T, where Q and Z are orthogonal matrices, P is an upper triangular matrix, and S is a quasi-triangular matrix with 1-by-1 and 2-by-2 diagonal blocks. The 1-by-1 blocks correspond to real eigenvalues of the matrix pair (H,T) and the 2-by-2 blocks correspond to complex conjugate pairs of eigenvalues. Additionally, the 2-by-2 upper triangular diagonal blocks of P corresponding to 2-by-2 blocks of S are reduced to positive diagonal form, i.e., if S(j+1,j) is non-zero, then P(j+1,j) = P(j,j+1) = 0, P(j,j) > 0, and P(j+1,j+1) > 0. Optionally, the orthogonal matrix Q from the generalized Schur factorization may be postmultiplied into an input matrix Q1, and the orthogonal matrix Z may be postmultiplied into an input matrix Z1. If Q1 and Z1 are the orthogonal matrices from DGGHRD that reduced the matrix pair (A,B) to generalized upper Hessenberg form, then the output matrices Q1*Q and Z1*Z are the orthogonal factors from the generalized Schur factorization of (A,B): A = (Q1*Q)*S*(Z1*Z)**T, B = (Q1*Q)*P*(Z1*Z)**T. To avoid overflow, eigenvalues of the matrix pair (H,T) (equivalently, of (A,B)) are computed as a pair of values (alpha,beta), where alpha is complex and beta real. If beta is nonzero, lambda = alpha / beta is an eigenvalue of the generalized nonsymmetric eigenvalue problem (GNEP) A*x = lambda*B*x and if alpha is nonzero, mu = beta / alpha is an eigenvalue of the alternate form of the GNEP mu*A*y = B*y. Real eigenvalues can be read directly from the generalized Schur form: alpha = S(i,i), beta = P(i,i). Ref: C.B. Moler Eigenvalue Problems", SIAM J. Numer. Anal., 10(1973), pp. 241&ndash;256. Ref: B. Kagstrom, D. Kressner, "Multishift Variants of the QZ Algorithm with Aggressive Early Deflation", SIAM J. Numer. Anal., 29(2006), pp. 199&ndash;227. Ref: T. Steel, D. Camps, K. Meerbergen, R. Vandebril "A multishift, multipole rational QZ method with agressive early deflation".
recursive subroutine, public	la_dlaqz3 (ilschur, ilq, ilz, n, ilo, ihi, nw, a, lda, b, ldb, q, ldq, z, ldz, ns, nd, alphar, alphai, beta, qc, ldqc, zc, ldzc, work, lwork, rec, info)
	DLAQZ3: performs AED.
pure subroutine, public	la_dlarre (range, n, vl, vu, il, iu, d, e, e2, rtol1, rtol2, spltol, nsplit, isplit, m, w, werr, wgap, iblock, indexw, gers, pivmin, work, iwork, info)
	To find the desired eigenvalues of a given real symmetric tridiagonal matrix T, DLARRE: sets any "small" off-diagonal elements to zero, and for each unreduced block T_i, it finds (a) a suitable shift at one end of the block's spectrum, (b) the base representation, T_i - sigma_i I = L_i D_i L_i^T, and (c) eigenvalues of each L_i D_i L_i^T. The representations and eigenvalues found are then used by DSTEMR to compute the eigenvectors of T. The accuracy varies depending on whether bisection is used to find a few eigenvalues or the dqds algorithm (subroutine DLASQ2) to conpute all and then discard any unwanted one. As an added benefit, DLARRE also outputs the n Gerschgorin intervals for the matrices L_i D_i L_i^T.
pure subroutine, public	la_dlasd0 (n, sqre, d, e, u, ldu, vt, ldvt, smlsiz, iwork, work, info)
	Using a divide and conquer approach, DLASD0: computes the singular value decomposition (SVD) of a real upper bidiagonal N-by-M matrix B with diagonal D and offdiagonal E, where M = N + SQRE. The algorithm computes orthogonal matrices U and VT such that B = U * S * VT. The singular values S are overwritten on D. A related subroutine, DLASDA, computes only the singular values, and optionally, the singular vectors in compact form.
pure subroutine, public	la_dlasda (icompq, smlsiz, n, sqre, d, e, u, ldu, vt, k, difl, difr, z, poles, givptr, givcol, ldgcol, perm, givnum, c, s, work, iwork, info)
	Using a divide and conquer approach, DLASDA: computes the singular value decomposition (SVD) of a real upper bidiagonal N-by-M matrix B with diagonal D and offdiagonal E, where M = N + SQRE. The algorithm computes the singular values in the SVD B = U * S * VT. The orthogonal matrices U and VT are optionally computed in compact form. A related subroutine, DLASD0, computes the singular values and the singular vectors in explicit form.
pure subroutine, public	la_dlasdq (uplo, sqre, n, ncvt, nru, ncc, d, e, vt, ldvt, u, ldu, c, ldc, work, info)
	DLASDQ: computes the singular value decomposition (SVD) of a real (upper or lower) bidiagonal matrix with diagonal D and offdiagonal E, accumulating the transformations if desired. Letting B denote the input bidiagonal matrix, the algorithm computes orthogonal matrices Q and P such that B = Q * S * P**T (P**T denotes the transpose of P). The singular values S are overwritten on D. The input matrix U is changed to U * Q if desired. The input matrix VT is changed to P**T * VT if desired. The input matrix C is changed to Q**T * C if desired. See "Computing Small Singular Values of Bidiagonal Matrices With Guaranteed High Relative Accuracy," by J. Demmel and W. Kahan, LAPACK Working Note #3, for a detailed description of the algorithm.
pure subroutine, public	la_dlasq1 (n, d, e, work, info)
	DLASQ1: computes the singular values of a real N-by-N bidiagonal matrix with diagonal D and off-diagonal E. The singular values are computed to high relative accuracy, in the absence of denormalization, underflow and overflow. The algorithm was first presented in "Accurate singular values and differential qd algorithms" by K. V. Fernando and B. N. Parlett, Numer. Math., Vol-67, No. 2, pp. 191-230, 1994, and the present implementation is described in "An implementation of the dqds Algorithm (Positive Case)", LAPACK Working Note.
pure subroutine, public	la_dlasq2 (n, z, info)
	DLASQ2: computes all the eigenvalues of the symmetric positive definite tridiagonal matrix associated with the qd array Z to high relative accuracy are computed to high relative accuracy, in the absence of denormalization, underflow and overflow. To see the relation of Z to the tridiagonal matrix, let L be a unit lower bidiagonal matrix with subdiagonals Z(2,4,6,,..) and let U be an upper bidiagonal matrix with 1's above and diagonal Z(1,3,5,,..). The tridiagonal is L*U or, if you prefer, the symmetric tridiagonal to which it is similar. Note : DLASQ2 defines a logical variable, IEEE, which is true on machines which follow ieee-754 floating-point standard in their handling of infinities and NaNs, and false otherwise. This variable is passed to DLASQ3.
pure subroutine, public	la_dlasyf_aa (uplo, j1, m, nb, a, lda, ipiv, h, ldh, work)
	DLATRF_AA factorizes a panel of a real symmetric matrix A using the Aasen's algorithm. The panel consists of a set of NB rows of A when UPLO is U, or a set of NB columns when UPLO is L. In order to factorize the panel, the Aasen's algorithm requires the last row, or column, of the previous panel. The first row, or column, of A is set to be the first row, or column, of an identity matrix, which is used to factorize the first panel. The resulting J-th row of U, or J-th column of L, is stored in the (J-1)-th row, or column, of A (without the unit diagonals), while the diagonal and subdiagonal of A are overwritten by those of T.
pure subroutine, public	la_dpteqr (compz, n, d, e, z, ldz, work, info)
	DPTEQR: computes all eigenvalues and, optionally, eigenvectors of a symmetric positive definite tridiagonal matrix by first factoring the matrix using DPTTRF, and then calling DBDSQR to compute the singular values of the bidiagonal factor. This routine computes the eigenvalues of the positive definite tridiagonal matrix to high relative accuracy. This means that if the eigenvalues range over many orders of magnitude in size, then the small eigenvalues and corresponding eigenvectors will be computed more accurately than, for example, with the standard QR method. The eigenvectors of a full or band symmetric positive definite matrix can also be found if DSYTRD, DSPTRD, or DSBTRD has been used to reduce this matrix to tridiagonal form. (The reduction to tridiagonal form, however, may preclude the possibility of obtaining high relative accuracy in the small eigenvalues of the original matrix, if these eigenvalues range over many orders of magnitude.)
pure subroutine, public	la_dstegr (jobz, range, n, d, e, vl, vu, il, iu, abstol, m, w, z, ldz, isuppz, work, lwork, iwork, liwork, info)
	DSTEGR: computes selected eigenvalues and, optionally, eigenvectors of a real symmetric tridiagonal matrix T. Any such unreduced matrix has a well defined set of pairwise different real eigenvalues, the corresponding real eigenvectors are pairwise orthogonal. The spectrum may be computed either completely or partially by specifying either an interval (VL,VU] or a range of indices IL:IU for the desired eigenvalues. DSTEGR is a compatibility wrapper around the improved DSTEMR routine. See DSTEMR for further details. One important change is that the ABSTOL parameter no longer provides any benefit and hence is no longer used. Note : DSTEGR and DSTEMR work only on machines which follow IEEE-754 floating-point standard in their handling of infinities and NaNs. Normal execution may create these exceptiona values and hence may abort due to a floating point exception in environments which do not conform to the IEEE-754 standard.
pure subroutine, public	la_dstemr (jobz, range, n, d, e, vl, vu, il, iu, m, w, z, ldz, nzc, isuppz, tryrac, work, lwork, iwork, liwork, info)
	DSTEMR: computes selected eigenvalues and, optionally, eigenvectors of a real symmetric tridiagonal matrix T. Any such unreduced matrix has a well defined set of pairwise different real eigenvalues, the corresponding real eigenvectors are pairwise orthogonal. The spectrum may be computed either completely or partially by specifying either an interval (VL,VU] or a range of indices IL:IU for the desired eigenvalues. Depending on the number of desired eigenvalues, these are computed either by bisection or the dqds algorithm. Numerically orthogonal eigenvectors are computed by the use of various suitable L D L^T factorizations near clusters of close eigenvalues (referred to as RRRs, Relatively Robust Representations). An informal sketch of the algorithm follows. For each unreduced block (submatrix) of T, (a) Compute T - sigma I = L D L^T, so that L and D define all the wanted eigenvalues to high relative accuracy. This means that small relative changes in the entries of D and L cause only small relative changes in the eigenvalues and eigenvectors. The standard (unfactored) representation of the tridiagonal matrix T does not have this property in general. (b) Compute the eigenvalues to suitable accuracy. If the eigenvectors are desired, the algorithm attains full accuracy of the computed eigenvalues only right before the corresponding vectors have to be computed, see steps c) and d). (c) For each cluster of close eigenvalues, select a new shift close to the cluster, find a new factorization, and refine the shifted eigenvalues to suitable accuracy. (d) For each eigenvalue with a large enough relative separation compute the corresponding eigenvector by forming a rank revealing twisted factorization. Go back to (c) for any clusters that remain. For more details, see:
pure subroutine, public	la_dstevr (jobz, range, n, d, e, vl, vu, il, iu, abstol, m, w, z, ldz, isuppz, work, lwork, iwork, liwork, info)
	DSTEVR: computes selected eigenvalues and, optionally, eigenvectors of a real symmetric tridiagonal matrix T. Eigenvalues and eigenvectors can be selected by specifying either a range of values or a range of indices for the desired eigenvalues. Whenever possible, DSTEVR calls DSTEMR to compute the eigenspectrum using Relatively Robust Representations. DSTEMR computes eigenvalues by the dqds algorithm, while orthogonal eigenvectors are computed from various "good" L D L^T representations (also known as Relatively Robust Representations). Gram-Schmidt orthogonalization is avoided as far as possible. More specifically, the various steps of the algorithm are as follows. For the i-th unreduced block of T, (a) Compute T - sigma_i = L_i D_i L_i^T, such that L_i D_i L_i^T is a relatively robust representation, (b) Compute the eigenvalues, lambda_j, of L_i D_i L_i^T to high relative accuracy by the dqds algorithm, (c) If there is a cluster of close eigenvalues, "choose" sigma_i close to the cluster, and go to step (a), (d) Given the approximate eigenvalue lambda_j of L_i D_i L_i^T, compute the corresponding eigenvector by forming a rank-revealing twisted factorization. The desired accuracy of the output can be specified by the input parameter ABSTOL. For more details, see "A new O(n^2) algorithm for the symmetric tridiagonal eigenvalue/eigenvector problem", by Inderjit Dhillon, Computer Science Division Technical Report No. UCB//CSD-97-971, UC Berkeley, May 1997. Note 1 : DSTEVR calls DSTEMR when the full spectrum is requested on machines which conform to the ieee-754 floating point standard. DSTEVR calls DSTEBZ and DSTEIN on non-ieee machines and when partial spectrum requests are made. Normal execution of DSTEMR may create NaNs and infinities and hence may abort due to a floating point exception in environments which do not handle NaNs and infinities in the ieee standard default manner.
subroutine, public	la_dsyevr (jobz, range, uplo, n, a, lda, vl, vu, il, iu, abstol, m, w, z, ldz, isuppz, work, lwork, iwork, liwork, info)
	DSYEVR: computes selected eigenvalues and, optionally, eigenvectors of a real symmetric matrix A. Eigenvalues and eigenvectors can be selected by specifying either a range of values or a range of indices for the desired eigenvalues. DSYEVR first reduces the matrix A to tridiagonal form T with a call to DSYTRD. Then, whenever possible, DSYEVR calls DSTEMR to compute the eigenspectrum using Relatively Robust Representations. DSTEMR computes eigenvalues by the dqds algorithm, while orthogonal eigenvectors are computed from various "good" L D L^T representations (also known as Relatively Robust Representations). Gram-Schmidt orthogonalization is avoided as far as possible. More specifically, the various steps of the algorithm are as follows. For each unreduced block (submatrix) of T, (a) Compute T - sigma I = L D L^T, so that L and D define all the wanted eigenvalues to high relative accuracy. This means that small relative changes in the entries of D and L cause only small relative changes in the eigenvalues and eigenvectors. The standard (unfactored) representation of the tridiagonal matrix T does not have this property in general. (b) Compute the eigenvalues to suitable accuracy. If the eigenvectors are desired, the algorithm attains full accuracy of the computed eigenvalues only right before the corresponding vectors have to be computed, see steps c) and d). (c) For each cluster of close eigenvalues, select a new shift close to the cluster, find a new factorization, and refine the shifted eigenvalues to suitable accuracy. (d) For each eigenvalue with a large enough relative separation compute the corresponding eigenvector by forming a rank revealing twisted factorization. Go back to (c) for any clusters that remain. The desired accuracy of the output can be specified by the input parameter ABSTOL. For more details, see DSTEMR's documentation and:
pure subroutine, public	la_dsysv_aa (uplo, n, nrhs, a, lda, ipiv, b, ldb, work, lwork, info)
	DSYSV computes the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric matrix and X and B are N-by-NRHS matrices. Aasen's algorithm is used to factor A as A = U**T * T * U, if UPLO = 'U', or A = L * T * L**T, if UPLO = 'L', where U (or L) is a product of permutation and unit upper (lower) triangular matrices, and T is symmetric tridiagonal. The factored form of A is then used to solve the system of equations A * X = B.
pure subroutine, public	la_dsytrf_aa (uplo, n, a, lda, ipiv, work, lwork, info)
	DSYTRF_AA: computes the factorization of a real symmetric matrix A using the Aasen's algorithm. The form of the factorization is A = U**T*T*U or A = L*T*L**T where U (or L) is a product of permutation and unit upper (lower) triangular matrices, and T is a symmetric tridiagonal matrix. This is the blocked version of the algorithm, calling Level 3 BLAS.

Function/Subroutine Documentation

la_dbbcsd()

pure subroutine, public la_lapack_d::la_dbbcsd	(	character, intent(in)	jobu1,
		character, intent(in)	jobu2,
		character, intent(in)	jobv1t,
		character, intent(in)	jobv2t,
		character, intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	p,
		integer(ilp), intent(in)	q,
		real(dp), dimension(*), intent(inout)	theta,
		real(dp), dimension(*), intent(inout)	phi,
		real(dp), dimension(ldu1,*), intent(inout)	u1,
		integer(ilp), intent(in)	ldu1,
		real(dp), dimension(ldu2,*), intent(inout)	u2,
		integer(ilp), intent(in)	ldu2,
		real(dp), dimension(ldv1t,*), intent(inout)	v1t,
		integer(ilp), intent(in)	ldv1t,
		real(dp), dimension(ldv2t,*), intent(inout)	v2t,
		integer(ilp), intent(in)	ldv2t,
		real(dp), dimension(*), intent(out)	b11d,
		real(dp), dimension(*), intent(out)	b11e,
		real(dp), dimension(*), intent(out)	b12d,
		real(dp), dimension(*), intent(out)	b12e,
		real(dp), dimension(*), intent(out)	b21d,
		real(dp), dimension(*), intent(out)	b21e,
		real(dp), dimension(*), intent(out)	b22d,
		real(dp), dimension(*), intent(out)	b22e,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DBBCSD: computes the CS decomposition of an orthogonal matrix in bidiagonal-block form, [ B11 | B12 0 0 ] [ 0 | 0 -I 0 ] X = [-------------—] [ B21 | B22 0 0 ] [ 0 | 0 0 I ] [ C | -S 0 0 ] [ U1 | ] [ 0 | 0 -I 0 ] [ V1 | ]**T = [------—] [------------—] [------—] . [ | U2 ] [ S | C 0 0 ] [ | V2 ] [ 0 | 0 0 I ] X is M-by-M, its top-left block is P-by-Q, and Q must be no larger than P, M-P, or M-Q. (If Q is not the smallest index, then X must be transposed and/or permuted. This can be done in constant time using the TRANS and SIGNS options. See DORCSD for details.) The bidiagonal matrices B11, B12, B21, and B22 are represented implicitly by angles THETA(1:Q) and PHI(1:Q-1). The orthogonal matrices U1, U2, V1T, and V2T are input/output. The input matrices are pre- or post-multiplied by the appropriate singular vector matrices.

Here is the call graph for this function:

la_dbdsdc()

pure subroutine, public la_lapack_d::la_dbdsdc	(	character, intent(in)	uplo,
		character, intent(in)	compq,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(inout)	e,
		real(dp), dimension(ldu,*), intent(out)	u,
		integer(ilp), intent(in)	ldu,
		real(dp), dimension(ldvt,*), intent(out)	vt,
		integer(ilp), intent(in)	ldvt,
		real(dp), dimension(*), intent(out)	q,
		integer(ilp), dimension(*), intent(out)	iq,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DBDSDC: computes the singular value decomposition (SVD) of a real N-by-N (upper or lower) bidiagonal matrix B: B = U * S * VT, using a divide and conquer method, where S is a diagonal matrix with non-negative diagonal elements (the singular values of B), and U and VT are orthogonal matrices of left and right singular vectors, respectively. DBDSDC can be used to compute all singular values, and optionally, singular vectors or singular vectors in compact form. This code makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none. See DLASD3 for details. The code currently calls DLASDQ if singular values only are desired. However, it can be slightly modified to compute singular values using the divide and conquer method.

Here is the call graph for this function:

la_dbdsqr()

pure subroutine, public la_lapack_d::la_dbdsqr	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ncvt,
		integer(ilp), intent(in)	nru,
		integer(ilp), intent(in)	ncc,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(inout)	e,
		real(dp), dimension(ldvt,*), intent(inout)	vt,
		integer(ilp), intent(in)	ldvt,
		real(dp), dimension(ldu,*), intent(inout)	u,
		integer(ilp), intent(in)	ldu,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DBDSQR: computes the singular values and, optionally, the right and/or left singular vectors from the singular value decomposition (SVD) of a real N-by-N (upper or lower) bidiagonal matrix B using the implicit zero-shift QR algorithm. The SVD of B has the form B = Q * S * P**T where S is the diagonal matrix of singular values, Q is an orthogonal matrix of left singular vectors, and P is an orthogonal matrix of right singular vectors. If left singular vectors are requested, this subroutine actually returns U*Q instead of Q, and, if right singular vectors are requested, this subroutine returns P**T*VT instead of P**T, for given real input matrices U and VT. When U and VT are the orthogonal matrices that reduce a general matrix A to bidiagonal form: A = U*B*VT, as computed by DGEBRD, then A = (U*Q) * S * (P**T*VT) is the SVD of A. Optionally, the subroutine may also compute Q**T*C for a given real input matrix C. See "Computing Small Singular Values of Bidiagonal Matrices With Guaranteed High Relative Accuracy," by J. Demmel and W. Kahan, LAPACK Working Note #3 (or SIAM J. Sci. Statist. Comput. vol. 11, no. 5, pp. 873-912, Sept 1990) and "Accurate singular values and differential qd algorithms," by B. Parlett and V. Fernando, Technical Report CPAM-554, Mathematics Department, University of California at Berkeley, July 1992 for a detailed description of the algorithm.

Here is the call graph for this function:

la_ddisna()

pure subroutine, public la_lapack_d::la_ddisna	(	character, intent(in)	job,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(out)	sep,
		integer(ilp), intent(out)	info
	)

DDISNA: computes the reciprocal condition numbers for the eigenvectors of a real symmetric or complex Hermitian matrix or for the left or right singular vectors of a general m-by-n matrix. The reciprocal condition number is the 'gap' between the corresponding eigenvalue or singular value and the nearest other one. The bound on the error, measured by angle in radians, in the I-th computed vector is given by DLAMCH( 'E' ) * ( ANORM / SEP( I ) ) where ANORM = 2-norm(A) = max( abs( D(j) ) ). SEP(I) is not allowed to be smaller than DLAMCH( 'E' )*ANORM in order to limit the size of the error bound. DDISNA may also be used to compute error bounds for eigenvectors of the generalized symmetric definite eigenproblem.

Here is the call graph for this function:

la_dgbbrd()

pure subroutine, public la_lapack_d::la_dgbbrd	(	character, intent(in)	vect,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ncc,
		integer(ilp), intent(in)	kl,
		integer(ilp), intent(in)	ku,
		real(dp), dimension(ldab,*), intent(inout)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(*), intent(out)	d,
		real(dp), dimension(*), intent(out)	e,
		real(dp), dimension(ldq,*), intent(out)	q,
		integer(ilp), intent(in)	ldq,
		real(dp), dimension(ldpt,*), intent(out)	pt,
		integer(ilp), intent(in)	ldpt,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DGBBRD: reduces a real general m-by-n band matrix A to upper bidiagonal form B by an orthogonal transformation: Q**T * A * P = B. The routine computes B, and optionally forms Q or P**T, or computes Q**T*C for a given matrix C.

Here is the call graph for this function:

la_dgbcon()

pure subroutine, public la_lapack_d::la_dgbcon	(	character, intent(in)	norm,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kl,
		integer(ilp), intent(in)	ku,
		real(dp), dimension(ldab,*), intent(in)	ab,
		integer(ilp), intent(in)	ldab,
		integer(ilp), dimension(*), intent(in)	ipiv,
		real(dp), intent(in)	anorm,
		real(dp), intent(out)	rcond,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DGBCON: estimates the reciprocal of the condition number of a real general band matrix A, in either the 1-norm or the infinity-norm, using the LU factorization computed by DGBTRF. An estimate is obtained for norm(inv(A)), and the reciprocal of the condition number is computed as RCOND = 1 / ( norm(A) * norm(inv(A)) ).

Here is the call graph for this function:

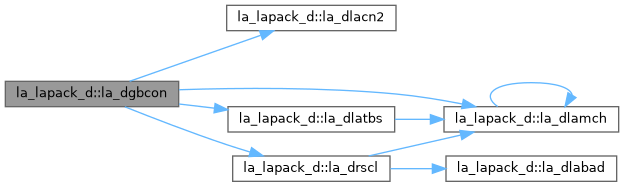
la_dgbequ()

pure subroutine, public la_lapack_d::la_dgbequ	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kl,
		integer(ilp), intent(in)	ku,
		real(dp), dimension(ldab,*), intent(in)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(*), intent(out)	r,
		real(dp), dimension(*), intent(out)	c,
		real(dp), intent(out)	rowcnd,
		real(dp), intent(out)	colcnd,
		real(dp), intent(out)	amax,
		integer(ilp), intent(out)	info
	)

DGBEQU: computes row and column scalings intended to equilibrate an M-by-N band matrix A and reduce its condition number. R returns the row scale factors and C the column scale factors, chosen to try to make the largest element in each row and column of the matrix B with elements B(i,j)=R(i)*A(i,j)*C(j) have absolute value 1. R(i) and C(j) are restricted to be between SMLNUM = smallest safe number and BIGNUM = largest safe number. Use of these scaling factors is not guaranteed to reduce the condition number of A but works well in practice.

Here is the call graph for this function:

la_dgbequb()

pure subroutine, public la_lapack_d::la_dgbequb	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kl,
		integer(ilp), intent(in)	ku,
		real(dp), dimension(ldab,*), intent(in)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(*), intent(out)	r,
		real(dp), dimension(*), intent(out)	c,
		real(dp), intent(out)	rowcnd,
		real(dp), intent(out)	colcnd,
		real(dp), intent(out)	amax,
		integer(ilp), intent(out)	info
	)

DGBEQUB: computes row and column scalings intended to equilibrate an M-by-N matrix A and reduce its condition number. R returns the row scale factors and C the column scale factors, chosen to try to make the largest element in each row and column of the matrix B with elements B(i,j)=R(i)*A(i,j)*C(j) have an absolute value of at most the radix. R(i) and C(j) are restricted to be a power of the radix between SMLNUM = smallest safe number and BIGNUM = largest safe number. Use of these scaling factors is not guaranteed to reduce the condition number of A but works well in practice. This routine differs from DGEEQU by restricting the scaling factors to a power of the radix. Barring over- and underflow, scaling by these factors introduces no additional rounding errors. However, the scaled entries' magnitudes are no longer approximately 1 but lie between sqrt(radix) and 1/sqrt(radix).

Here is the call graph for this function:

la_dgbrfs()

pure subroutine, public la_lapack_d::la_dgbrfs	(	character, intent(in)	trans,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kl,
		integer(ilp), intent(in)	ku,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(ldab,*), intent(in)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(ldafb,*), intent(in)	afb,
		integer(ilp), intent(in)	ldafb,
		integer(ilp), dimension(*), intent(in)	ipiv,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldx,*), intent(inout)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), dimension(*), intent(out)	ferr,
		real(dp), dimension(*), intent(out)	berr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DGBRFS: improves the computed solution to a system of linear equations when the coefficient matrix is banded, and provides error bounds and backward error estimates for the solution.

Here is the call graph for this function:

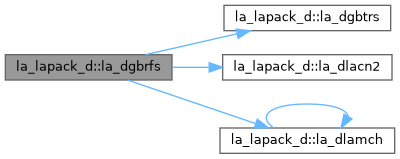
la_dgbsv()

pure subroutine, public la_lapack_d::la_dgbsv	(	integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kl,
		integer(ilp), intent(in)	ku,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(ldab,*), intent(inout)	ab,
		integer(ilp), intent(in)	ldab,
		integer(ilp), dimension(*), intent(out)	ipiv,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	info
	)

DGBSV: computes the solution to a real system of linear equations A * X = B, where A is a band matrix of order N with KL subdiagonals and KU superdiagonals, and X and B are N-by-NRHS matrices. The LU decomposition with partial pivoting and row interchanges is used to factor A as A = L * U, where L is a product of permutation and unit lower triangular matrices with KL subdiagonals, and U is upper triangular with KL+KU superdiagonals. The factored form of A is then used to solve the system of equations A * X = B.

Here is the call graph for this function:

la_dgbsvx()

subroutine, public la_lapack_d::la_dgbsvx	(	character, intent(in)	fact,
		character, intent(in)	trans,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kl,
		integer(ilp), intent(in)	ku,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(ldab,*), intent(inout)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(ldafb,*), intent(inout)	afb,
		integer(ilp), intent(in)	ldafb,
		integer(ilp), dimension(*), intent(inout)	ipiv,
		character, intent(inout)	equed,
		real(dp), dimension(*), intent(inout)	r,
		real(dp), dimension(*), intent(inout)	c,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldx,*), intent(out)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), intent(out)	rcond,
		real(dp), dimension(*), intent(out)	ferr,
		real(dp), dimension(*), intent(out)	berr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DGBSVX: uses the LU factorization to compute the solution to a real system of linear equations A * X = B, A**T * X = B, or A**H * X = B, where A is a band matrix of order N with KL subdiagonals and KU superdiagonals, and X and B are N-by-NRHS matrices. Error bounds on the solution and a condition estimate are also provided.

Here is the call graph for this function:

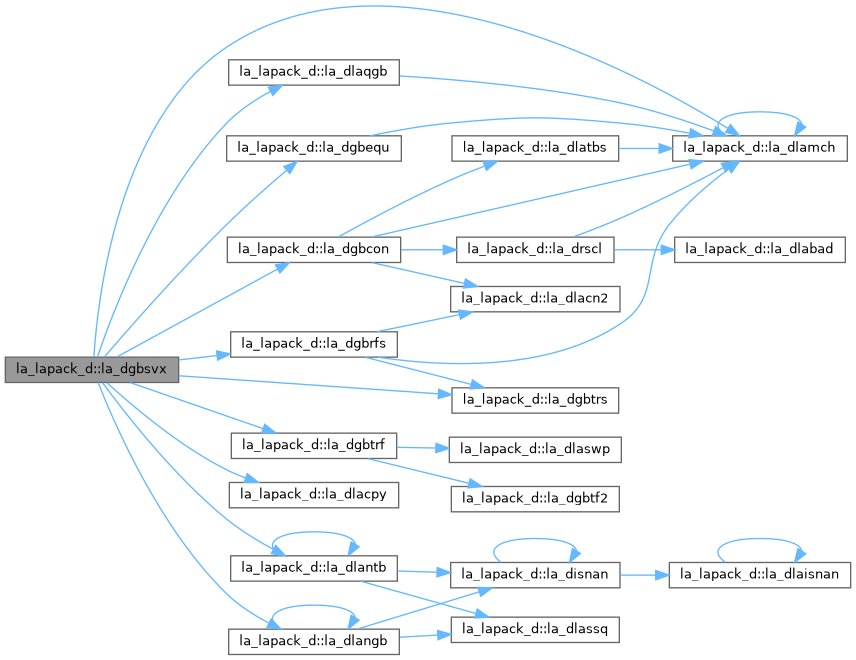
la_dgbtf2()

pure subroutine, public la_lapack_d::la_dgbtf2	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kl,
		integer(ilp), intent(in)	ku,
		real(dp), dimension(ldab,*), intent(inout)	ab,
		integer(ilp), intent(in)	ldab,
		integer(ilp), dimension(*), intent(out)	ipiv,
		integer(ilp), intent(out)	info
	)

DGBTF2: computes an LU factorization of a real m-by-n band matrix A using partial pivoting with row interchanges. This is the unblocked version of the algorithm, calling Level 2 BLAS.

la_dgbtrf()

pure subroutine, public la_lapack_d::la_dgbtrf	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kl,
		integer(ilp), intent(in)	ku,
		real(dp), dimension(ldab,*), intent(inout)	ab,
		integer(ilp), intent(in)	ldab,
		integer(ilp), dimension(*), intent(out)	ipiv,
		integer(ilp), intent(out)	info
	)

DGBTRF: computes an LU factorization of a real m-by-n band matrix A using partial pivoting with row interchanges. This is the blocked version of the algorithm, calling Level 3 BLAS.

Here is the call graph for this function:

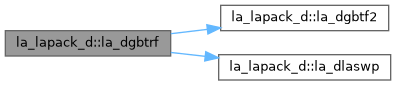
la_dgbtrs()

pure subroutine, public la_lapack_d::la_dgbtrs	(	character, intent(in)	trans,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kl,
		integer(ilp), intent(in)	ku,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(ldab,*), intent(in)	ab,
		integer(ilp), intent(in)	ldab,
		integer(ilp), dimension(*), intent(in)	ipiv,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	info
	)

DGBTRS: solves a system of linear equations A * X = B or A**T * X = B with a general band matrix A using the LU factorization computed by DGBTRF.

la_dgebak()

pure subroutine, public la_lapack_d::la_dgebak	(	character, intent(in)	job,
		character, intent(in)	side,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ilo,
		integer(ilp), intent(in)	ihi,
		real(dp), dimension(*), intent(in)	scale,
		integer(ilp), intent(in)	m,
		real(dp), dimension(ldv,*), intent(inout)	v,
		integer(ilp), intent(in)	ldv,
		integer(ilp), intent(out)	info
	)

DGEBAK: forms the right or left eigenvectors of a real general matrix by backward transformation on the computed eigenvectors of the balanced matrix output by DGEBAL.

la_dgebal()

pure subroutine, public la_lapack_d::la_dgebal	(	character, intent(in)	job,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), intent(out)	ilo,
		integer(ilp), intent(out)	ihi,
		real(dp), dimension(*), intent(out)	scale,
		integer(ilp), intent(out)	info
	)

DGEBAL: balances a general real matrix A. This involves, first, permuting A by a similarity transformation to isolate eigenvalues in the first 1 to ILO-1 and last IHI+1 to N elements on the diagonal; and second, applying a diagonal similarity transformation to rows and columns ILO to IHI to make the rows and columns as close in norm as possible. Both steps are optional. Balancing may reduce the 1-norm of the matrix, and improve the accuracy of the computed eigenvalues and/or eigenvectors.

Here is the call graph for this function:

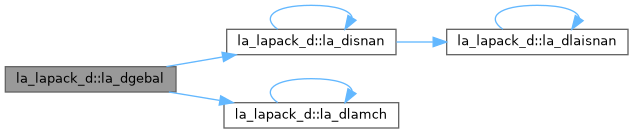
la_dgebd2()

pure subroutine, public la_lapack_d::la_dgebd2	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	d,
		real(dp), dimension(*), intent(out)	e,
		real(dp), dimension(*), intent(out)	tauq,
		real(dp), dimension(*), intent(out)	taup,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DGEBD2: reduces a real general m by n matrix A to upper or lower bidiagonal form B by an orthogonal transformation: Q**T * A * P = B. If m >= n, B is upper bidiagonal; if m < n, B is lower bidiagonal.

Here is the call graph for this function:

la_dgebrd()

pure subroutine, public la_lapack_d::la_dgebrd	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	d,
		real(dp), dimension(*), intent(out)	e,
		real(dp), dimension(*), intent(out)	tauq,
		real(dp), dimension(*), intent(out)	taup,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGEBRD: reduces a general real M-by-N matrix A to upper or lower bidiagonal form B by an orthogonal transformation: Q**T * A * P = B. If m >= n, B is upper bidiagonal; if m < n, B is lower bidiagonal.

Here is the call graph for this function:

la_dgecon()

pure subroutine, public la_lapack_d::la_dgecon	(	character, intent(in)	norm,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), intent(in)	anorm,
		real(dp), intent(out)	rcond,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DGECON: estimates the reciprocal of the condition number of a general real matrix A, in either the 1-norm or the infinity-norm, using the LU factorization computed by DGETRF. An estimate is obtained for norm(inv(A)), and the reciprocal of the condition number is computed as RCOND = 1 / ( norm(A) * norm(inv(A)) ).

Here is the call graph for this function:

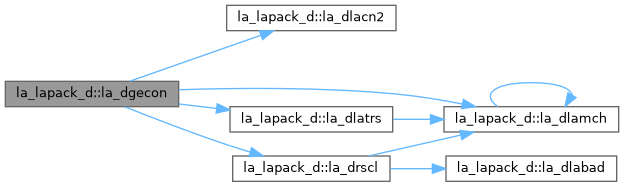
la_dgeequ()

pure subroutine, public la_lapack_d::la_dgeequ	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	r,
		real(dp), dimension(*), intent(out)	c,
		real(dp), intent(out)	rowcnd,
		real(dp), intent(out)	colcnd,
		real(dp), intent(out)	amax,
		integer(ilp), intent(out)	info
	)

DGEEQU: computes row and column scalings intended to equilibrate an M-by-N matrix A and reduce its condition number. R returns the row scale factors and C the column scale factors, chosen to try to make the largest element in each row and column of the matrix B with elements B(i,j)=R(i)*A(i,j)*C(j) have absolute value 1. R(i) and C(j) are restricted to be between SMLNUM = smallest safe number and BIGNUM = largest safe number. Use of these scaling factors is not guaranteed to reduce the condition number of A but works well in practice.

Here is the call graph for this function:

la_dgeequb()

pure subroutine, public la_lapack_d::la_dgeequb	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	r,
		real(dp), dimension(*), intent(out)	c,
		real(dp), intent(out)	rowcnd,
		real(dp), intent(out)	colcnd,
		real(dp), intent(out)	amax,
		integer(ilp), intent(out)	info
	)

DGEEQUB: computes row and column scalings intended to equilibrate an M-by-N matrix A and reduce its condition number. R returns the row scale factors and C the column scale factors, chosen to try to make the largest element in each row and column of the matrix B with elements B(i,j)=R(i)*A(i,j)*C(j) have an absolute value of at most the radix. R(i) and C(j) are restricted to be a power of the radix between SMLNUM = smallest safe number and BIGNUM = largest safe number. Use of these scaling factors is not guaranteed to reduce the condition number of A but works well in practice. This routine differs from DGEEQU by restricting the scaling factors to a power of the radix. Barring over- and underflow, scaling by these factors introduces no additional rounding errors. However, the scaled entries' magnitudes are no longer approximately 1 but lie between sqrt(radix) and 1/sqrt(radix).

Here is the call graph for this function:

la_dgees()

subroutine, public la_lapack_d::la_dgees	(	character, intent(in)	jobvs,
		character, intent(in)	sort,
		procedure(la_select_d)	select,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), intent(out)	sdim,
		real(dp), dimension(*), intent(out)	wr,
		real(dp), dimension(*), intent(out)	wi,
		real(dp), dimension(ldvs,*), intent(out)	vs,
		integer(ilp), intent(in)	ldvs,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		logical(lk), dimension(*), intent(out)	bwork,
		integer(ilp), intent(out)	info
	)

DGEES: computes for an N-by-N real nonsymmetric matrix A, the eigenvalues, the real Schur form T, and, optionally, the matrix of Schur vectors Z. This gives the Schur factorization A = Z*T*(Z**T). Optionally, it also orders the eigenvalues on the diagonal of the real Schur form so that selected eigenvalues are at the top left. The leading columns of Z then form an orthonormal basis for the invariant subspace corresponding to the selected eigenvalues. A matrix is in real Schur form if it is upper quasi-triangular with 1-by-1 and 2-by-2 blocks. 2-by-2 blocks will be standardized in the form [ a b ] [ c a ] where b*c < 0. The eigenvalues of such a block are a +- sqrt(bc).

Here is the call graph for this function:

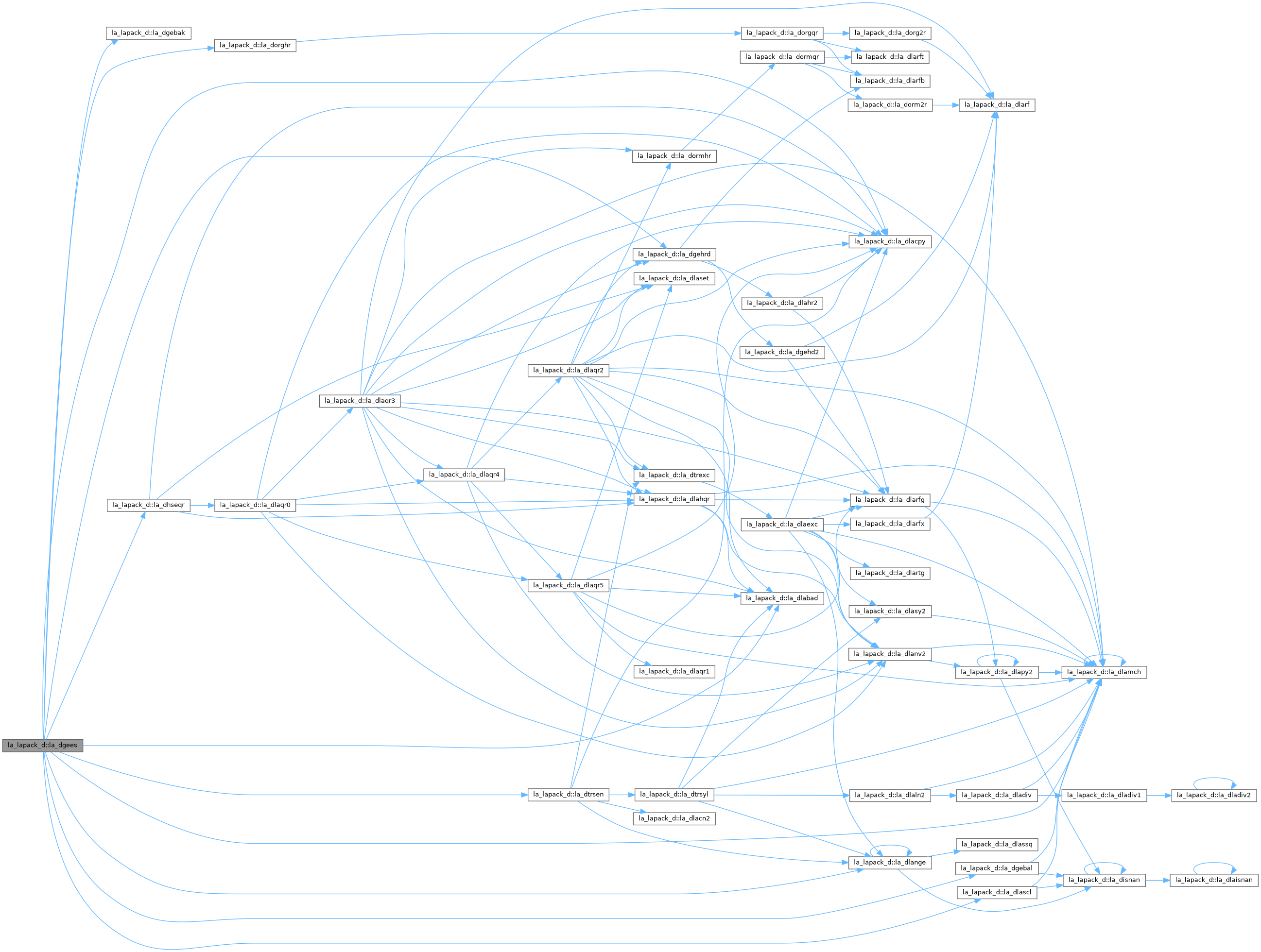
la_dgeesx()

subroutine, public la_lapack_d::la_dgeesx	(	character, intent(in)	jobvs,
		character, intent(in)	sort,
		procedure(la_select_d)	select,
		character, intent(in)	sense,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), intent(out)	sdim,
		real(dp), dimension(*), intent(out)	wr,
		real(dp), dimension(*), intent(out)	wi,
		real(dp), dimension(ldvs,*), intent(out)	vs,
		integer(ilp), intent(in)	ldvs,
		real(dp), intent(out)	rconde,
		real(dp), intent(out)	rcondv,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(in)	liwork,
		logical(lk), dimension(*), intent(out)	bwork,
		integer(ilp), intent(out)	info
	)

DGEESX: computes for an N-by-N real nonsymmetric matrix A, the eigenvalues, the real Schur form T, and, optionally, the matrix of Schur vectors Z. This gives the Schur factorization A = Z*T*(Z**T). Optionally, it also orders the eigenvalues on the diagonal of the real Schur form so that selected eigenvalues are at the top left; computes a reciprocal condition number for the average of the selected eigenvalues (RCONDE); and computes a reciprocal condition number for the right invariant subspace corresponding to the selected eigenvalues (RCONDV). The leading columns of Z form an orthonormal basis for this invariant subspace. For further explanation of the reciprocal condition numbers RCONDE and RCONDV, see Section 4.10_dp of the LAPACK Users' Guide (where these quantities are called s and sep respectively). A real matrix is in real Schur form if it is upper quasi-triangular with 1-by-1 and 2-by-2 blocks. 2-by-2 blocks will be standardized in the form [ a b ] [ c a ] where b*c < 0. The eigenvalues of such a block are a +- sqrt(bc).

Here is the call graph for this function:

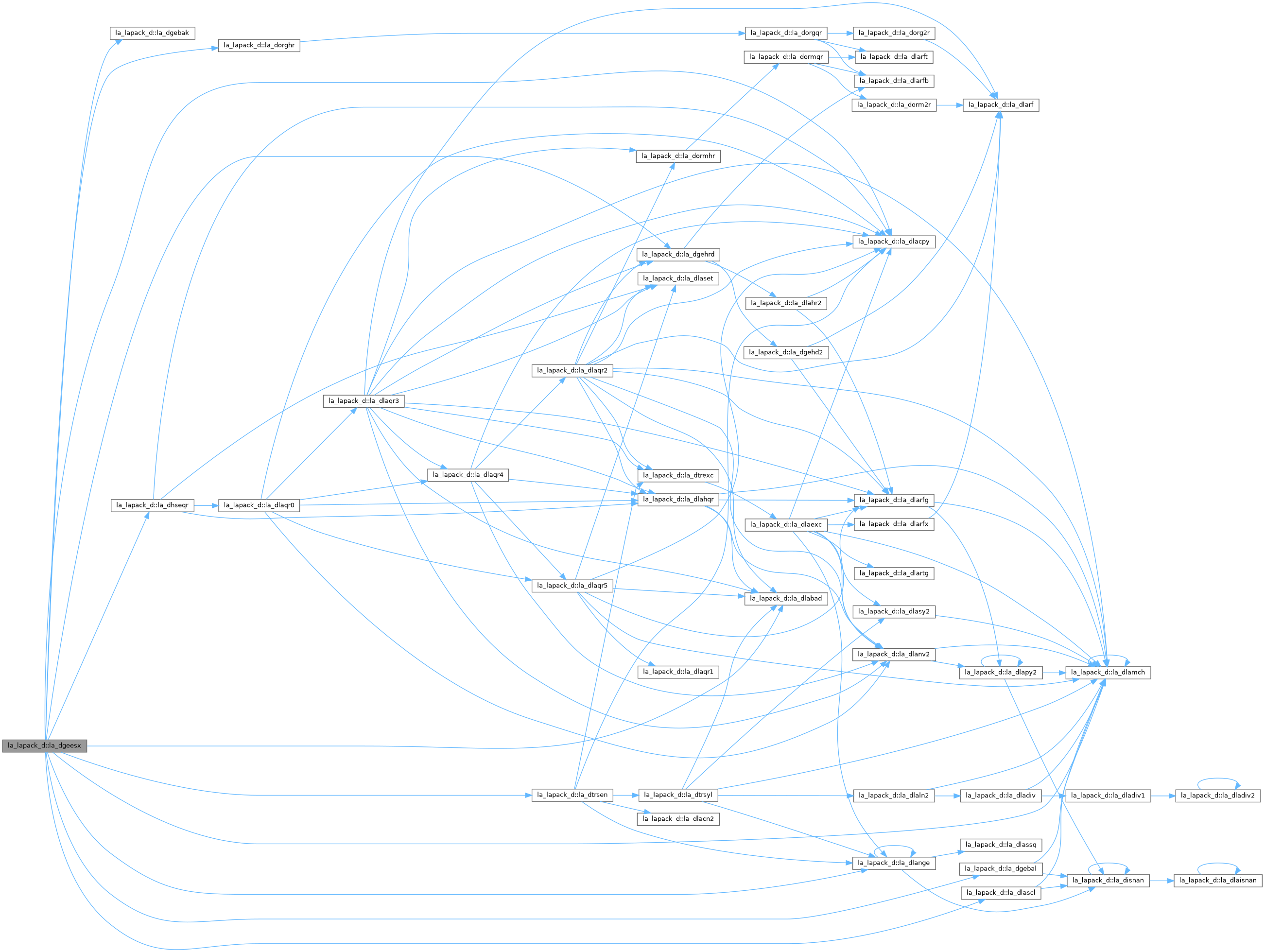
la_dgeev()

subroutine, public la_lapack_d::la_dgeev	(	character, intent(in)	jobvl,
		character, intent(in)	jobvr,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	wr,
		real(dp), dimension(*), intent(out)	wi,
		real(dp), dimension(ldvl,*), intent(out)	vl,
		integer(ilp), intent(in)	ldvl,
		real(dp), dimension(ldvr,*), intent(out)	vr,
		integer(ilp), intent(in)	ldvr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGEEV: computes for an N-by-N real nonsymmetric matrix A, the eigenvalues and, optionally, the left and/or right eigenvectors. The right eigenvector v(j) of A satisfies A * v(j) = lambda(j) * v(j) where lambda(j) is its eigenvalue. The left eigenvector u(j) of A satisfies u(j)**H * A = lambda(j) * u(j)**H where u(j)**H denotes the conjugate-transpose of u(j). The computed eigenvectors are normalized to have Euclidean norm equal to 1 and largest component real.

Here is the call graph for this function:

la_dgeevx()

subroutine, public la_lapack_d::la_dgeevx	(	character, intent(in)	balanc,
		character, intent(in)	jobvl,
		character, intent(in)	jobvr,
		character, intent(in)	sense,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	wr,
		real(dp), dimension(*), intent(out)	wi,
		real(dp), dimension(ldvl,*), intent(out)	vl,
		integer(ilp), intent(in)	ldvl,
		real(dp), dimension(ldvr,*), intent(out)	vr,
		integer(ilp), intent(in)	ldvr,
		integer(ilp), intent(out)	ilo,
		integer(ilp), intent(out)	ihi,
		real(dp), dimension(*), intent(out)	scale,
		real(dp), intent(out)	abnrm,
		real(dp), dimension(*), intent(out)	rconde,
		real(dp), dimension(*), intent(out)	rcondv,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DGEEVX: computes for an N-by-N real nonsymmetric matrix A, the eigenvalues and, optionally, the left and/or right eigenvectors. Optionally also, it computes a balancing transformation to improve the conditioning of the eigenvalues and eigenvectors (ILO, IHI, SCALE, and ABNRM), reciprocal condition numbers for the eigenvalues (RCONDE), and reciprocal condition numbers for the right eigenvectors (RCONDV). The right eigenvector v(j) of A satisfies A * v(j) = lambda(j) * v(j) where lambda(j) is its eigenvalue. The left eigenvector u(j) of A satisfies u(j)**H * A = lambda(j) * u(j)**H where u(j)**H denotes the conjugate-transpose of u(j). The computed eigenvectors are normalized to have Euclidean norm equal to 1 and largest component real. Balancing a matrix means permuting the rows and columns to make it more nearly upper triangular, and applying a diagonal similarity transformation D * A * D**(-1), where D is a diagonal matrix, to make its rows and columns closer in norm and the condition numbers of its eigenvalues and eigenvectors smaller. The computed reciprocal condition numbers correspond to the balanced matrix. Permuting rows and columns will not change the condition numbers (in exact arithmetic) but diagonal scaling will. For further explanation of balancing, see section 4.10.2_dp of the LAPACK Users' Guide.

Here is the call graph for this function:

la_dgehd2()

pure subroutine, public la_lapack_d::la_dgehd2	(	integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ilo,
		integer(ilp), intent(in)	ihi,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	tau,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DGEHD2: reduces a real general matrix A to upper Hessenberg form H by an orthogonal similarity transformation: Q**T * A * Q = H .

Here is the call graph for this function:

la_dgehrd()

pure subroutine, public la_lapack_d::la_dgehrd	(	integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ilo,
		integer(ilp), intent(in)	ihi,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	tau,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGEHRD: reduces a real general matrix A to upper Hessenberg form H by an orthogonal similarity transformation: Q**T * A * Q = H .

Here is the call graph for this function:

la_dgejsv()

pure subroutine, public la_lapack_d::la_dgejsv	(	character, intent(in)	joba,
		character, intent(in)	jobu,
		character, intent(in)	jobv,
		character, intent(in)	jobr,
		character, intent(in)	jobt,
		character, intent(in)	jobp,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(n), intent(out)	sva,
		real(dp), dimension(ldu,*), intent(out)	u,
		integer(ilp), intent(in)	ldu,
		real(dp), dimension(ldv,*), intent(out)	v,
		integer(ilp), intent(in)	ldv,
		real(dp), dimension(lwork), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DGEJSV: computes the singular value decomposition (SVD) of a real M-by-N matrix [A], where M >= N. The SVD of [A] is written as [A] = [U] * [SIGMA] * [V]^t, where [SIGMA] is an N-by-N (M-by-N) matrix which is zero except for its N diagonal elements, [U] is an M-by-N (or M-by-M) orthonormal matrix, and [V] is an N-by-N orthogonal matrix. The diagonal elements of [SIGMA] are the singular values of [A]. The columns of [U] and [V] are the left and the right singular vectors of [A], respectively. The matrices [U] and [V] are computed and stored in the arrays U and V, respectively. The diagonal of [SIGMA] is computed and stored in the array SVA. DGEJSV can sometimes compute tiny singular values and their singular vectors much more accurately than other SVD routines, see below under Further Details.

Here is the call graph for this function:

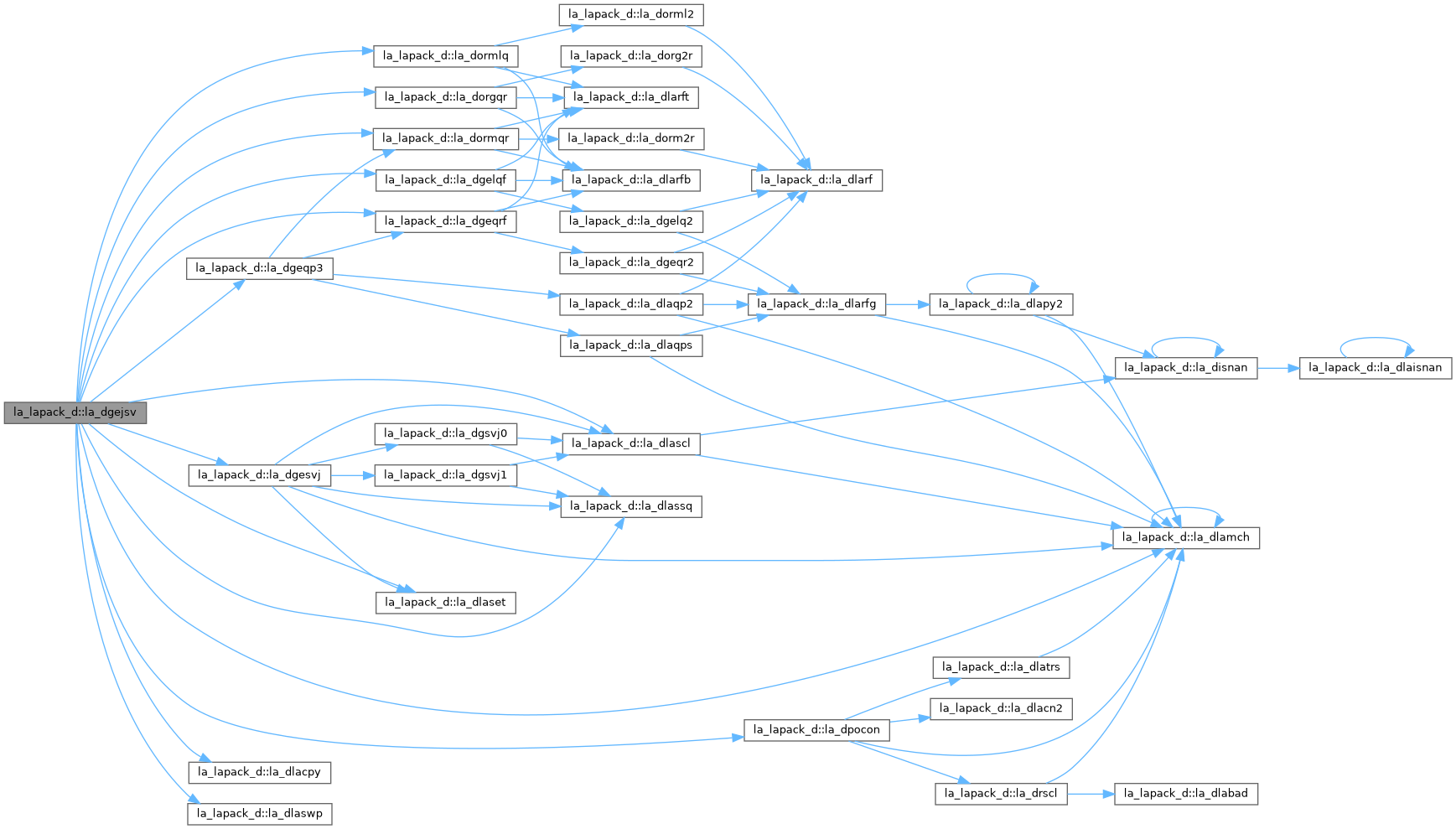
la_dgelq()

pure subroutine, public la_lapack_d::la_dgelq	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	t,
		integer(ilp), intent(in)	tsize,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGELQ: computes an LQ factorization of a real M-by-N matrix A: A = ( L 0 ) * Q where: Q is a N-by-N orthogonal matrix; L is a lower-triangular M-by-M matrix; 0 is a M-by-(N-M) zero matrix, if M < N.

Here is the call graph for this function:

la_dgelq2()

pure subroutine, public la_lapack_d::la_dgelq2	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	tau,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DGELQ2: computes an LQ factorization of a real m-by-n matrix A: A = ( L 0 ) * Q where: Q is a n-by-n orthogonal matrix; L is a lower-triangular m-by-m matrix; 0 is a m-by-(n-m) zero matrix, if m < n.

Here is the call graph for this function:

la_dgelqf()

pure subroutine, public la_lapack_d::la_dgelqf	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	tau,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGELQF: computes an LQ factorization of a real M-by-N matrix A: A = ( L 0 ) * Q where: Q is a N-by-N orthogonal matrix; L is a lower-triangular M-by-M matrix; 0 is a M-by-(N-M) zero matrix, if M < N.

Here is the call graph for this function:

la_dgelqt()

pure subroutine, public la_lapack_d::la_dgelqt	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	mb,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldt,*), intent(out)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DGELQT: computes a blocked LQ factorization of a real M-by-N matrix A using the compact WY representation of Q.

Here is the call graph for this function:

la_dgelqt3()

pure recursive subroutine, public la_lapack_d::la_dgelqt3	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldt,*), intent(out)	t,
		integer(ilp), intent(in)	ldt,
		integer(ilp), intent(out)	info
	)

DGELQT3: recursively computes a LQ factorization of a real M-by-N matrix A, using the compact WY representation of Q. Based on the algorithm of Elmroth and Gustavson, IBM J. Res. Develop. Vol 44 No. 4 July 2000.

Here is the call graph for this function:

la_dgels()

subroutine, public la_lapack_d::la_dgels	(	character, intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGELS: solves overdetermined or underdetermined real linear systems involving an M-by-N matrix A, or its transpose, using a QR or LQ factorization of A. It is assumed that A has full rank. The following options are provided:

1. If TRANS = 'N' and m >= n: find the least squares solution of an overdetermined system, i.e., solve the least squares problem minimize || B - A*X ||.
2. If TRANS = 'N' and m < n: find the minimum norm solution of an underdetermined system A * X = B.
3. If TRANS = 'T' and m >= n: find the minimum norm solution of an underdetermined system A**T * X = B.
4. If TRANS = 'T' and m < n: find the least squares solution of an overdetermined system, i.e., solve the least squares problem minimize || B - A**T * X ||. Several right hand side vectors b and solution vectors x can be handled in a single call; they are stored as the columns of the M-by-NRHS right hand side matrix B and the N-by-NRHS solution matrix X.

Here is the call graph for this function:

la_dgelsd()

subroutine, public la_lapack_d::la_dgelsd	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(*), intent(out)	s,
		real(dp), intent(in)	rcond,
		integer(ilp), intent(out)	rank,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DGELSD: computes the minimum-norm solution to a real linear least squares problem: minimize 2-norm(| b - A*x |) using the singular value decomposition (SVD) of A. A is an M-by-N matrix which may be rank-deficient. Several right hand side vectors b and solution vectors x can be handled in a single call; they are stored as the columns of the M-by-NRHS right hand side matrix B and the N-by-NRHS solution matrix X. The problem is solved in three steps: (1) Reduce the coefficient matrix A to bidiagonal form with Householder transformations, reducing the original problem into a "bidiagonal least squares problem" (BLS) (2) Solve the BLS using a divide and conquer approach. (3) Apply back all the Householder transformations to solve the original least squares problem. The effective rank of A is determined by treating as zero those singular values which are less than RCOND times the largest singular value. The divide and conquer algorithm makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none.

Here is the call graph for this function:

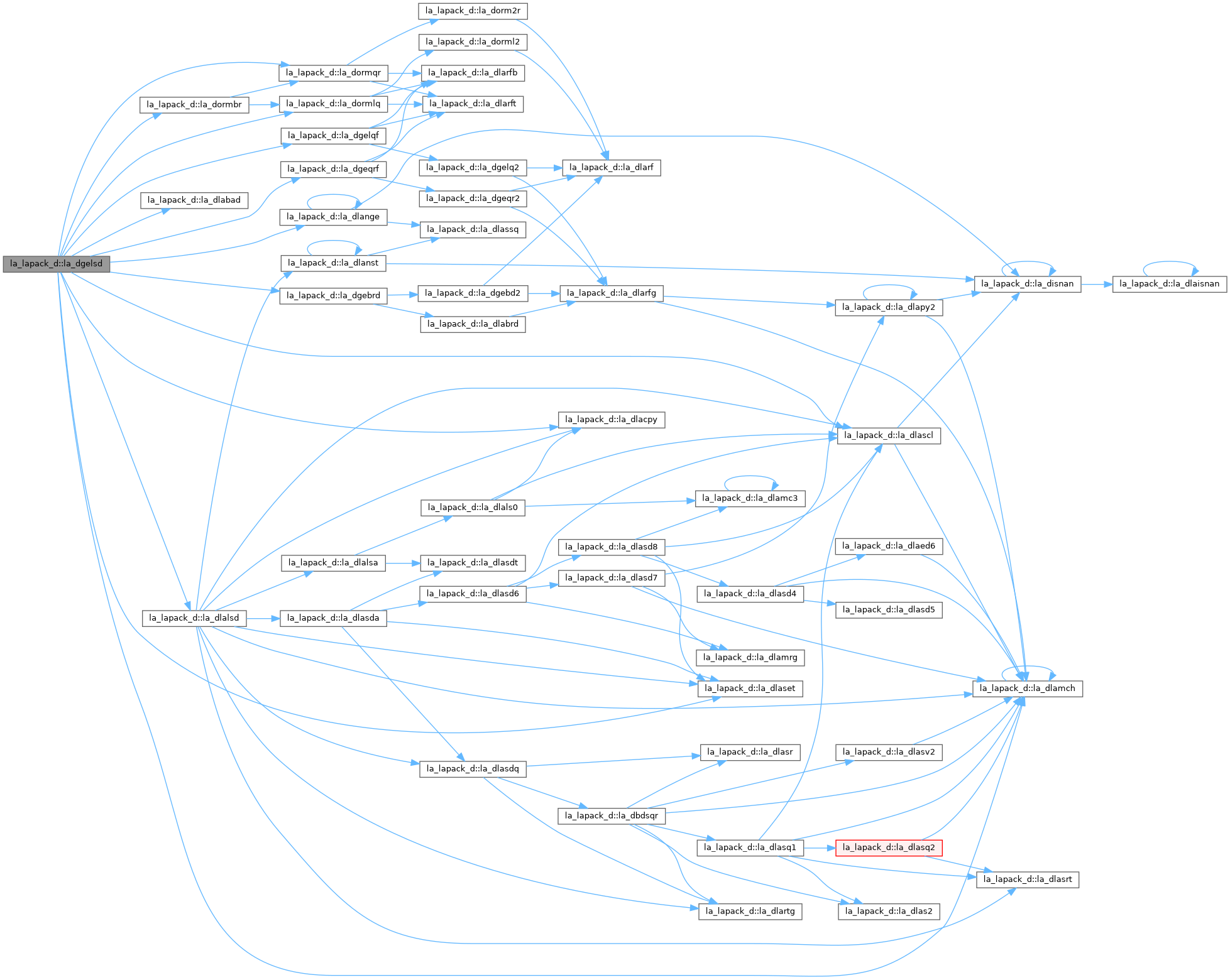
la_dgelss()

subroutine, public la_lapack_d::la_dgelss	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(*), intent(out)	s,
		real(dp), intent(in)	rcond,
		integer(ilp), intent(out)	rank,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGELSS: computes the minimum norm solution to a real linear least squares problem: Minimize 2-norm(| b - A*x |). using the singular value decomposition (SVD) of A. A is an M-by-N matrix which may be rank-deficient. Several right hand side vectors b and solution vectors x can be handled in a single call; they are stored as the columns of the M-by-NRHS right hand side matrix B and the N-by-NRHS solution matrix X. The effective rank of A is determined by treating as zero those singular values which are less than RCOND times the largest singular value.

Here is the call graph for this function:

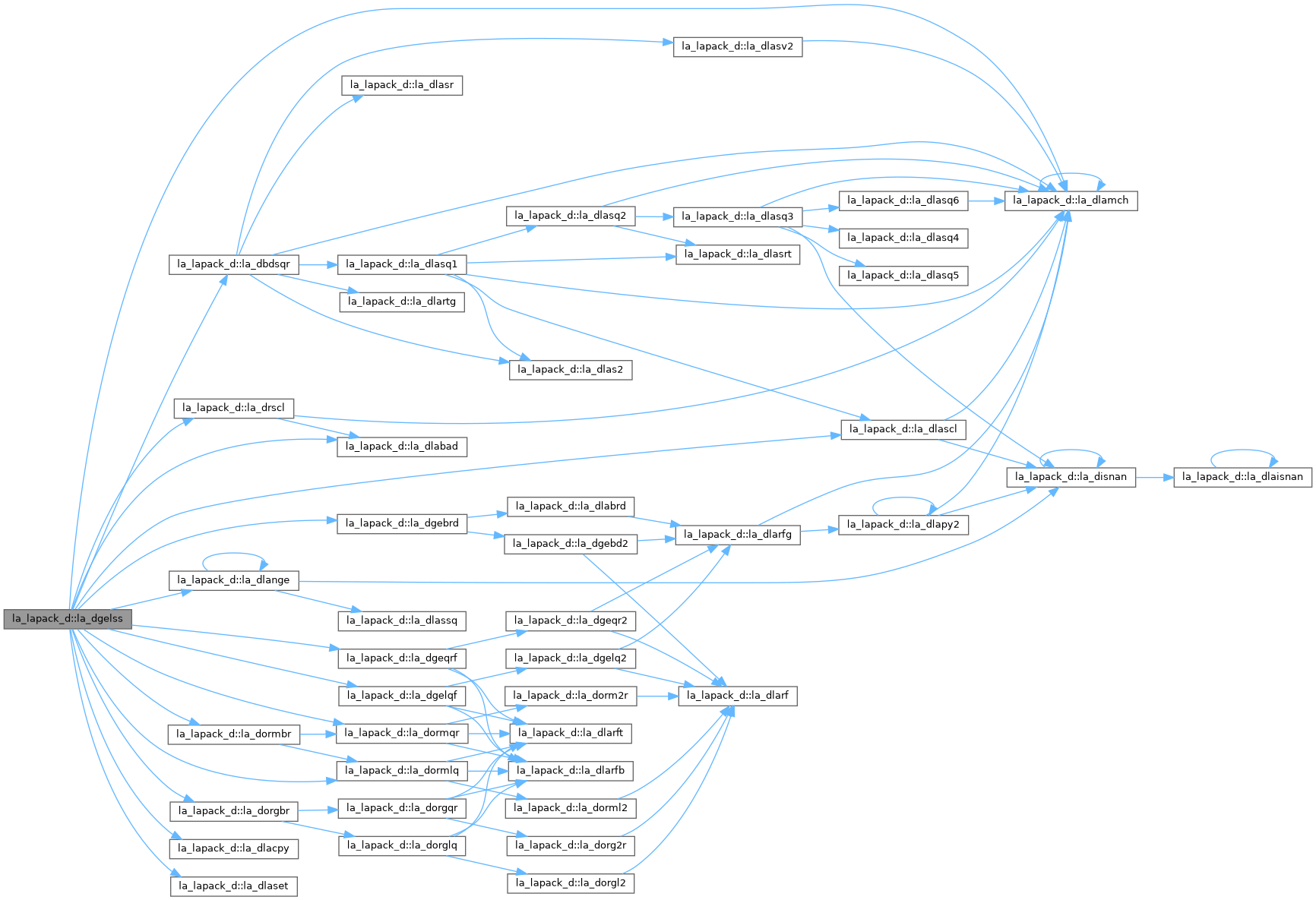
la_dgelsy()

subroutine, public la_lapack_d::la_dgelsy	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), dimension(*), intent(inout)	jpvt,
		real(dp), intent(in)	rcond,
		integer(ilp), intent(out)	rank,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGELSY: computes the minimum-norm solution to a real linear least squares problem: minimize || A * X - B || using a complete orthogonal factorization of A. A is an M-by-N matrix which may be rank-deficient. Several right hand side vectors b and solution vectors x can be handled in a single call; they are stored as the columns of the M-by-NRHS right hand side matrix B and the N-by-NRHS solution matrix X. The routine first computes a QR factorization with column pivoting: A * P = Q * [ R11 R12 ] [ 0 R22 ] with R11 defined as the largest leading submatrix whose estimated condition number is less than 1/RCOND. The order of R11, RANK, is the effective rank of A. Then, R22 is considered to be negligible, and R12 is annihilated by orthogonal transformations from the right, arriving at the complete orthogonal factorization: A * P = Q * [ T11 0 ] * Z [ 0 0 ] The minimum-norm solution is then X = P * Z**T [ inv(T11)*Q1**T*B ] [ 0 ] where Q1 consists of the first RANK columns of Q. This routine is basically identical to the original xGELSX except three differences: o The call to the subroutine xGEQPF has been substituted by the the call to the subroutine xGEQP3. This subroutine is a Blas-3 version of the QR factorization with column pivoting. o Matrix B (the right hand side) is updated with Blas-3. o The permutation of matrix B (the right hand side) is faster and more simple.

Here is the call graph for this function:

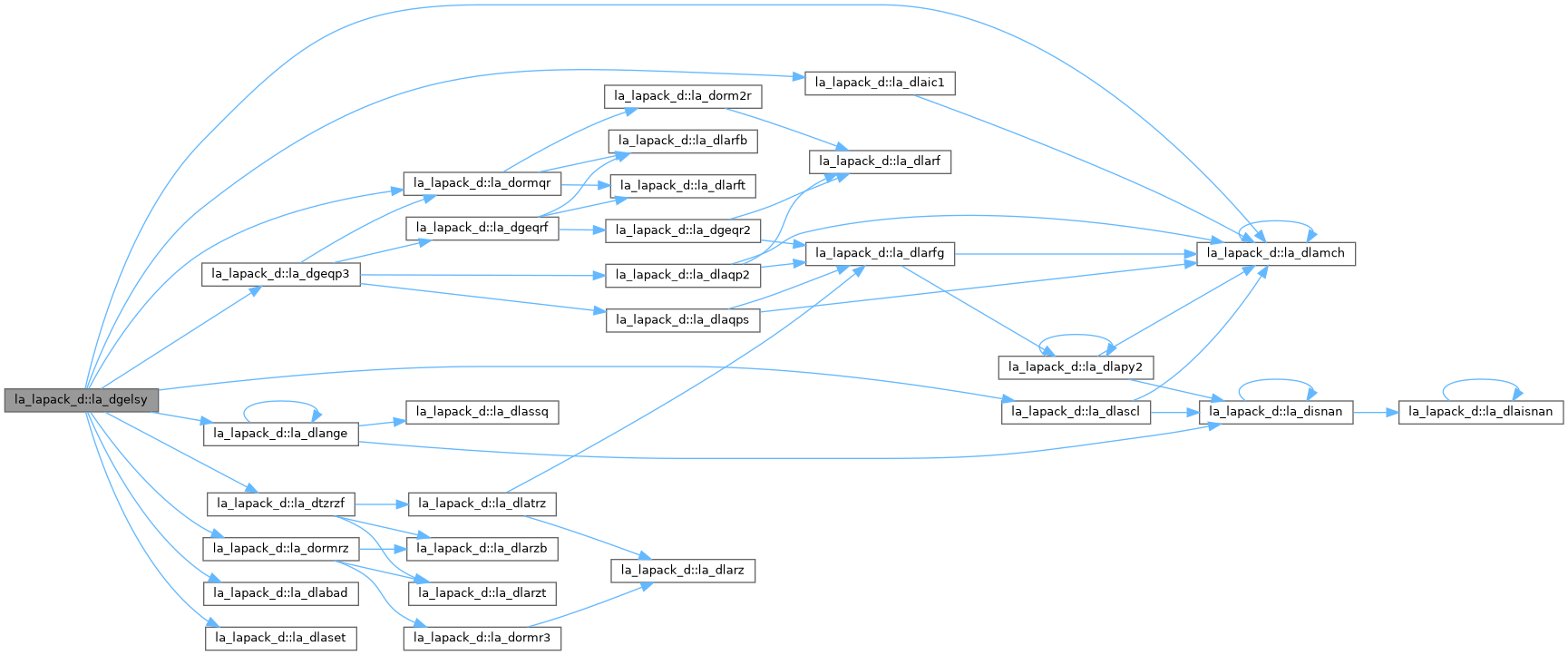
la_dgemlq()

pure subroutine, public la_lapack_d::la_dgemlq	(	character, intent(in)	side,
		character, intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	t,
		integer(ilp), intent(in)	tsize,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGEMLQ: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q * C C * Q TRANS = 'T': Q**T * C C * Q**T where Q is a real orthogonal matrix defined as the product of blocked elementary reflectors computed by short wide LQ factorization (DGELQ)

Here is the call graph for this function:

la_dgemlqt()

pure subroutine, public la_lapack_d::la_dgemlqt	(	character, intent(in)	side,
		character, intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		integer(ilp), intent(in)	mb,
		real(dp), dimension(ldv,*), intent(in)	v,
		integer(ilp), intent(in)	ldv,
		real(dp), dimension(ldt,*), intent(in)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DGEMLQT: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q C C Q TRANS = 'T': Q**T C C Q**T where Q is a real orthogonal matrix defined as the product of K elementary reflectors: Q = H(1) H(2) . . . H(K) = I - V T V**T generated using the compact WY representation as returned by DGELQT. Q is of order M if SIDE = 'L' and of order N if SIDE = 'R'.

Here is the call graph for this function:

la_dgemqr()

pure subroutine, public la_lapack_d::la_dgemqr	(	character, intent(in)	side,
		character, intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	t,
		integer(ilp), intent(in)	tsize,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGEMQR: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q * C C * Q TRANS = 'T': Q**T * C C * Q**T where Q is a real orthogonal matrix defined as the product of blocked elementary reflectors computed by tall skinny QR factorization (DGEQR)

Here is the call graph for this function:

la_dgemqrt()

pure subroutine, public la_lapack_d::la_dgemqrt	(	character, intent(in)	side,
		character, intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		integer(ilp), intent(in)	nb,
		real(dp), dimension(ldv,*), intent(in)	v,
		integer(ilp), intent(in)	ldv,
		real(dp), dimension(ldt,*), intent(in)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DGEMQRT: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q C C Q TRANS = 'T': Q**T C C Q**T where Q is a real orthogonal matrix defined as the product of K elementary reflectors: Q = H(1) H(2) . . . H(K) = I - V T V**T generated using the compact WY representation as returned by DGEQRT. Q is of order M if SIDE = 'L' and of order N if SIDE = 'R'.

Here is the call graph for this function:

la_dgeql2()

pure subroutine, public la_lapack_d::la_dgeql2	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	tau,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DGEQL2: computes a QL factorization of a real m by n matrix A: A = Q * L.

Here is the call graph for this function:

la_dgeqlf()

pure subroutine, public la_lapack_d::la_dgeqlf	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	tau,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGEQLF: computes a QL factorization of a real M-by-N matrix A: A = Q * L.

Here is the call graph for this function:

la_dgeqp3()

pure subroutine, public la_lapack_d::la_dgeqp3	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(inout)	jpvt,
		real(dp), dimension(*), intent(out)	tau,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGEQP3: computes a QR factorization with column pivoting of a matrix A: A*P = Q*R using Level 3 BLAS.

Here is the call graph for this function:

la_dgeqr()

pure subroutine, public la_lapack_d::la_dgeqr	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	t,
		integer(ilp), intent(in)	tsize,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGEQR: computes a QR factorization of a real M-by-N matrix A: A = Q * ( R ), ( 0 ) where: Q is a M-by-M orthogonal matrix; R is an upper-triangular N-by-N matrix; 0 is a (M-N)-by-N zero matrix, if M > N.

Here is the call graph for this function:

la_dgeqr2()

pure subroutine, public la_lapack_d::la_dgeqr2	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	tau,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DGEQR2: computes a QR factorization of a real m-by-n matrix A: A = Q * ( R ), ( 0 ) where: Q is a m-by-m orthogonal matrix; R is an upper-triangular n-by-n matrix; 0 is a (m-n)-by-n zero matrix, if m > n.

Here is the call graph for this function:

la_dgeqr2p()

subroutine, public la_lapack_d::la_dgeqr2p	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	tau,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DGEQR2P: computes a QR factorization of a real m-by-n matrix A: A = Q * ( R ), ( 0 ) where: Q is a m-by-m orthogonal matrix; R is an upper-triangular n-by-n matrix with nonnegative diagonal entries; 0 is a (m-n)-by-n zero matrix, if m > n.

Here is the call graph for this function:

la_dgeqrf()

pure subroutine, public la_lapack_d::la_dgeqrf	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	tau,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGEQRF: computes a QR factorization of a real M-by-N matrix A: A = Q * ( R ), ( 0 ) where: Q is a M-by-M orthogonal matrix; R is an upper-triangular N-by-N matrix; 0 is a (M-N)-by-N zero matrix, if M > N.

Here is the call graph for this function:

la_dgeqrfp()

subroutine, public la_lapack_d::la_dgeqrfp	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	tau,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGEQR2P computes a QR factorization of a real M-by-N matrix A: A = Q * ( R ), ( 0 ) where: Q is a M-by-M orthogonal matrix; R is an upper-triangular N-by-N matrix with nonnegative diagonal entries; 0 is a (M-N)-by-N zero matrix, if M > N.

Here is the call graph for this function:

la_dgeqrt()

pure subroutine, public la_lapack_d::la_dgeqrt	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nb,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldt,*), intent(out)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DGEQRT: computes a blocked QR factorization of a real M-by-N matrix A using the compact WY representation of Q.

Here is the call graph for this function:

la_dgeqrt2()

pure subroutine, public la_lapack_d::la_dgeqrt2	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldt,*), intent(out)	t,
		integer(ilp), intent(in)	ldt,
		integer(ilp), intent(out)	info
	)

DGEQRT2: computes a QR factorization of a real M-by-N matrix A, using the compact WY representation of Q.

Here is the call graph for this function:

la_dgeqrt3()

pure recursive subroutine, public la_lapack_d::la_dgeqrt3	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldt,*), intent(out)	t,
		integer(ilp), intent(in)	ldt,
		integer(ilp), intent(out)	info
	)

DGEQRT3: recursively computes a QR factorization of a real M-by-N matrix A, using the compact WY representation of Q. Based on the algorithm of Elmroth and Gustavson, IBM J. Res. Develop. Vol 44 No. 4 July 2000.

Here is the call graph for this function:

la_dgerfs()

pure subroutine, public la_lapack_d::la_dgerfs	(	character, intent(in)	trans,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldaf,*), intent(in)	af,
		integer(ilp), intent(in)	ldaf,
		integer(ilp), dimension(*), intent(in)	ipiv,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldx,*), intent(inout)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), dimension(*), intent(out)	ferr,
		real(dp), dimension(*), intent(out)	berr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DGERFS: improves the computed solution to a system of linear equations and provides error bounds and backward error estimates for the solution.

Here is the call graph for this function:

la_dgerq2()

pure subroutine, public la_lapack_d::la_dgerq2	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	tau,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DGERQ2: computes an RQ factorization of a real m by n matrix A: A = R * Q.

Here is the call graph for this function:

la_dgerqf()

pure subroutine, public la_lapack_d::la_dgerqf	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	tau,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGERQF: computes an RQ factorization of a real M-by-N matrix A: A = R * Q.

Here is the call graph for this function:

la_dgesc2()

pure subroutine, public la_lapack_d::la_dgesc2	(	integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(inout)	rhs,
		integer(ilp), dimension(*), intent(in)	ipiv,
		integer(ilp), dimension(*), intent(in)	jpiv,
		real(dp), intent(out)	scale
	)

DGESC2: solves a system of linear equations A * X = scale* RHS with a general N-by-N matrix A using the LU factorization with complete pivoting computed by DGETC2.

Here is the call graph for this function:

la_dgesdd()

subroutine, public la_lapack_d::la_dgesdd	(	character, intent(in)	jobz,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	s,
		real(dp), dimension(ldu,*), intent(out)	u,
		integer(ilp), intent(in)	ldu,
		real(dp), dimension(ldvt,*), intent(out)	vt,
		integer(ilp), intent(in)	ldvt,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DGESDD: computes the singular value decomposition (SVD) of a real M-by-N matrix A, optionally computing the left and right singular vectors. If singular vectors are desired, it uses a divide-and-conquer algorithm. The SVD is written A = U * SIGMA * transpose(V) where SIGMA is an M-by-N matrix which is zero except for its min(m,n) diagonal elements, U is an M-by-M orthogonal matrix, and V is an N-by-N orthogonal matrix. The diagonal elements of SIGMA are the singular values of A; they are real and non-negative, and are returned in descending order. The first min(m,n) columns of U and V are the left and right singular vectors of A. Note that the routine returns VT = V**T, not V. The divide and conquer algorithm makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none.

Here is the call graph for this function:

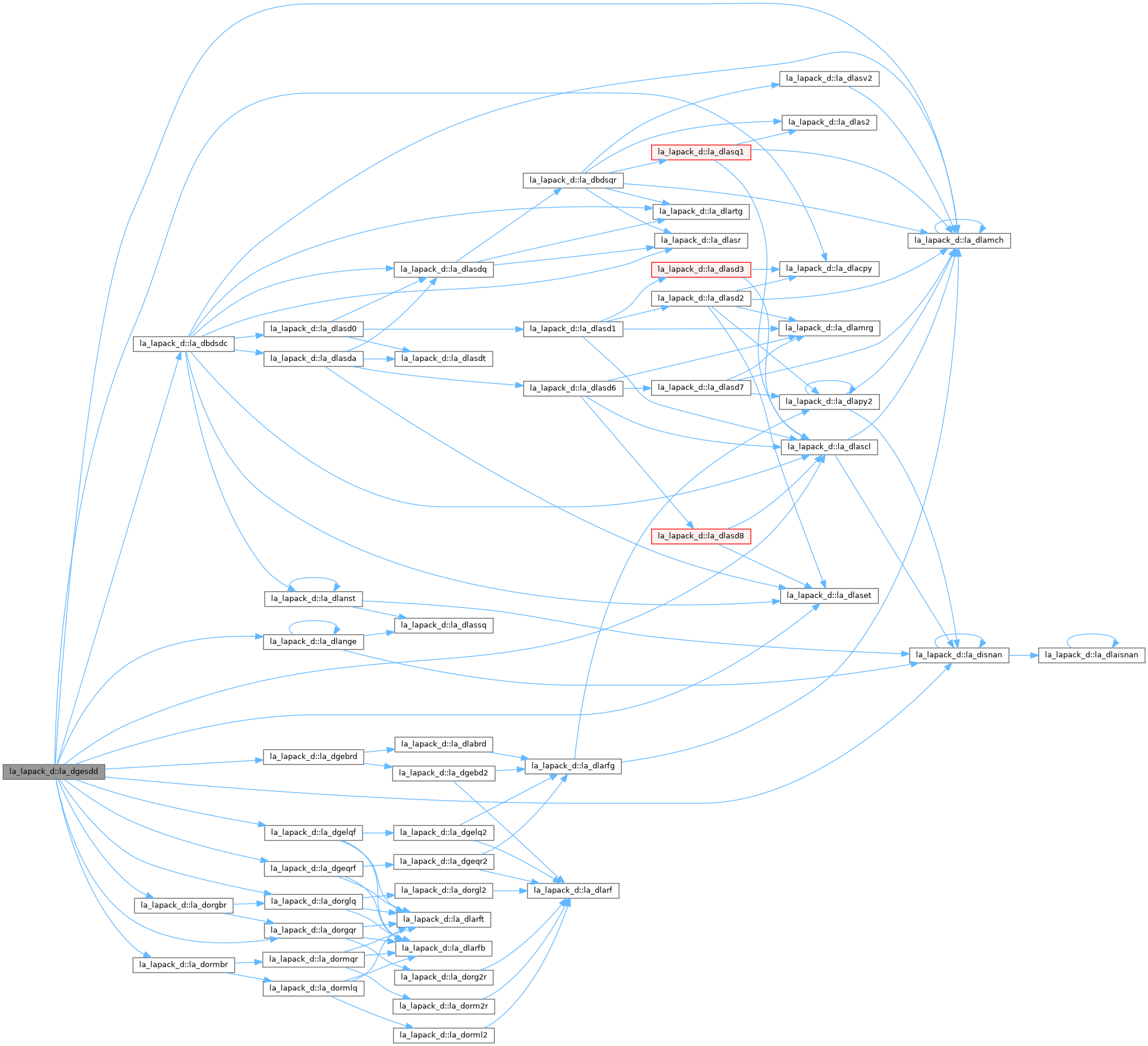
la_dgesv()

pure subroutine, public la_lapack_d::la_dgesv	(	integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(out)	ipiv,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	info
	)

DGESV: computes the solution to a real system of linear equations A * X = B, where A is an N-by-N matrix and X and B are N-by-NRHS matrices. The LU decomposition with partial pivoting and row interchanges is used to factor A as A = P * L * U, where P is a permutation matrix, L is unit lower triangular, and U is upper triangular. The factored form of A is then used to solve the system of equations A * X = B.

Here is the call graph for this function:

la_dgesvd()

subroutine, public la_lapack_d::la_dgesvd	(	character, intent(in)	jobu,
		character, intent(in)	jobvt,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	s,
		real(dp), dimension(ldu,*), intent(out)	u,
		integer(ilp), intent(in)	ldu,
		real(dp), dimension(ldvt,*), intent(out)	vt,
		integer(ilp), intent(in)	ldvt,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGESVD: computes the singular value decomposition (SVD) of a real M-by-N matrix A, optionally computing the left and/or right singular vectors. The SVD is written A = U * SIGMA * transpose(V) where SIGMA is an M-by-N matrix which is zero except for its min(m,n) diagonal elements, U is an M-by-M orthogonal matrix, and V is an N-by-N orthogonal matrix. The diagonal elements of SIGMA are the singular values of A; they are real and non-negative, and are returned in descending order. The first min(m,n) columns of U and V are the left and right singular vectors of A. Note that the routine returns V**T, not V.

Here is the call graph for this function:

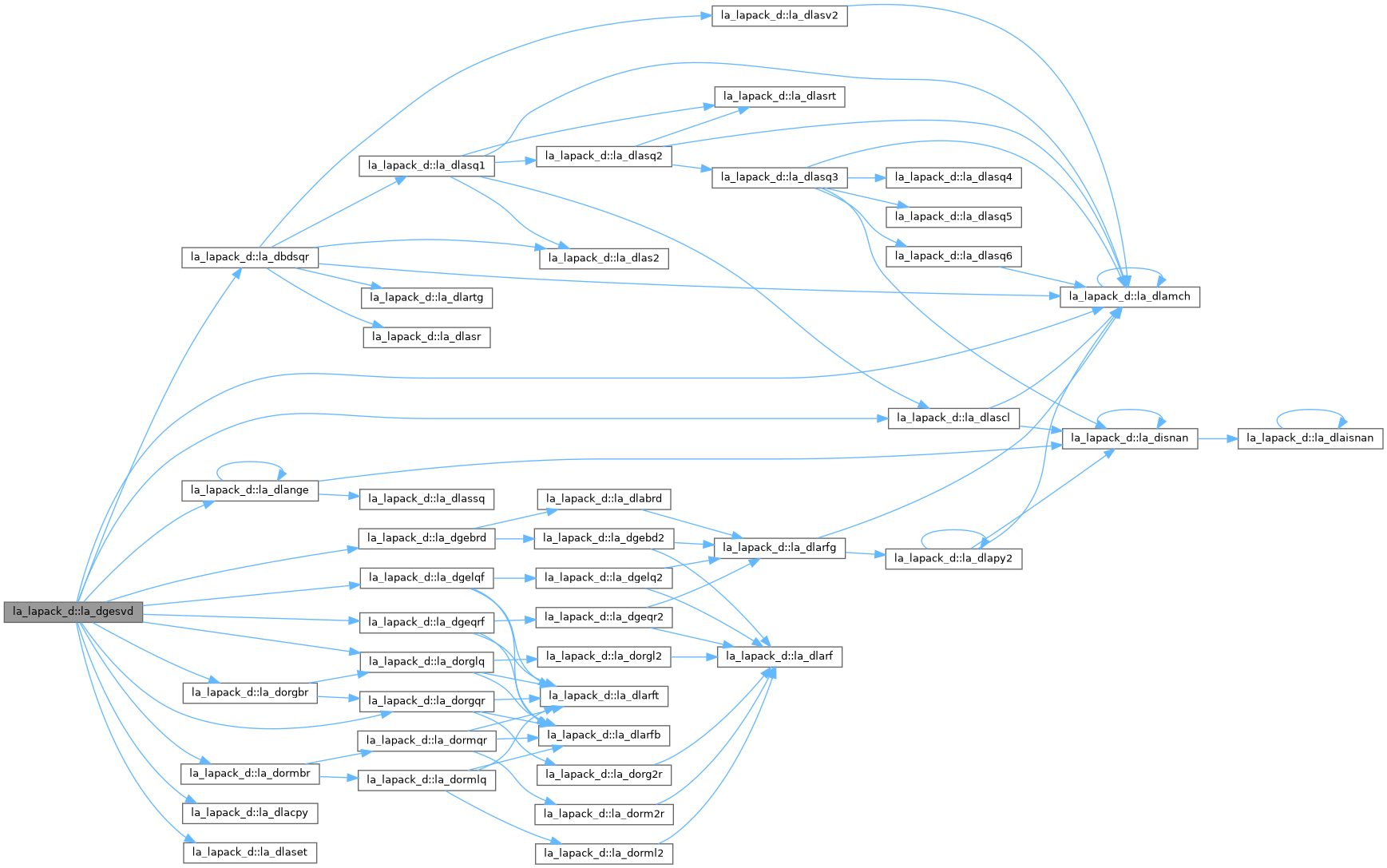
la_dgesvdq()

subroutine, public la_lapack_d::la_dgesvdq	(	character, intent(in)	joba,
		character, intent(in)	jobp,
		character, intent(in)	jobr,
		character, intent(in)	jobu,
		character, intent(in)	jobv,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	s,
		real(dp), dimension(ldu,*), intent(out)	u,
		integer(ilp), intent(in)	ldu,
		real(dp), dimension(ldv,*), intent(out)	v,
		integer(ilp), intent(in)	ldv,
		integer(ilp), intent(out)	numrank,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(in)	liwork,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(inout)	lwork,
		real(dp), dimension(*), intent(out)	rwork,
		integer(ilp), intent(in)	lrwork,
		integer(ilp), intent(out)	info
	)

DGESVDQ: computes the singular value decomposition (SVD) of a real M-by-N matrix A, where M >= N. The SVD of A is written as [++] [xx] [x0] [xx] A = U * SIGMA * V^*, [++] = [xx] * [ox] * [xx] [++] [xx] where SIGMA is an N-by-N diagonal matrix, U is an M-by-N orthonormal matrix, and V is an N-by-N orthogonal matrix. The diagonal elements of SIGMA are the singular values of A. The columns of U and V are the left and the right singular vectors of A, respectively.

Here is the call graph for this function:

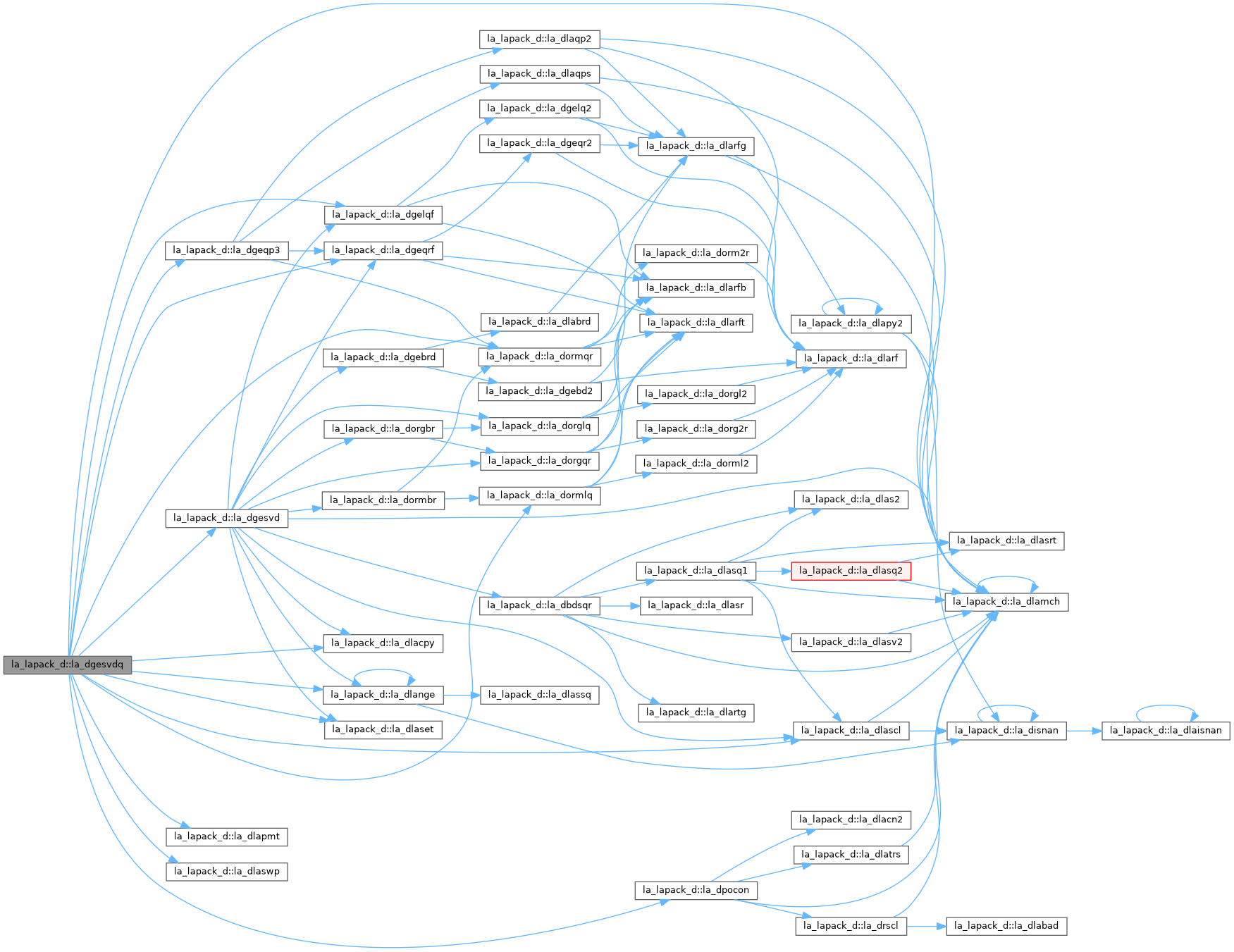
la_dgesvj()

pure subroutine, public la_lapack_d::la_dgesvj	(	character, intent(in)	joba,
		character, intent(in)	jobu,
		character, intent(in)	jobv,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(n), intent(out)	sva,
		integer(ilp), intent(in)	mv,
		real(dp), dimension(ldv,*), intent(inout)	v,
		integer(ilp), intent(in)	ldv,
		real(dp), dimension(lwork), intent(inout)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGESVJ: computes the singular value decomposition (SVD) of a real M-by-N matrix A, where M >= N. The SVD of A is written as [++] [xx] [x0] [xx] A = U * SIGMA * V^t, [++] = [xx] * [ox] * [xx] [++] [xx] where SIGMA is an N-by-N diagonal matrix, U is an M-by-N orthonormal matrix, and V is an N-by-N orthogonal matrix. The diagonal elements of SIGMA are the singular values of A. The columns of U and V are the left and the right singular vectors of A, respectively. DGESVJ can sometimes compute tiny singular values and their singular vectors much more accurately than other SVD routines, see below under Further Details.

Here is the call graph for this function:

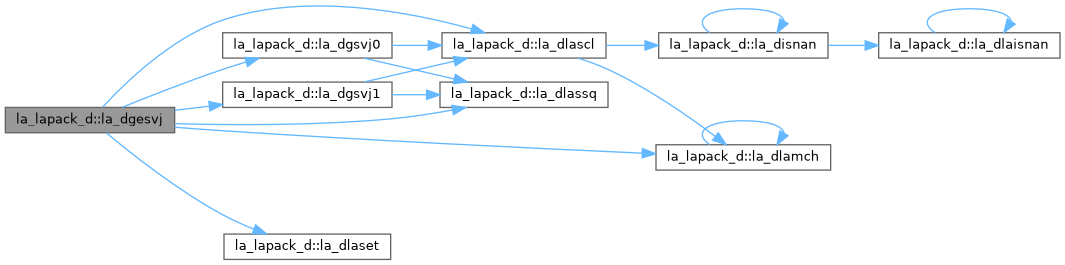
la_dgesvx()

subroutine, public la_lapack_d::la_dgesvx	(	character, intent(in)	fact,
		character, intent(in)	trans,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldaf,*), intent(inout)	af,
		integer(ilp), intent(in)	ldaf,
		integer(ilp), dimension(*), intent(inout)	ipiv,
		character, intent(inout)	equed,
		real(dp), dimension(*), intent(inout)	r,
		real(dp), dimension(*), intent(inout)	c,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldx,*), intent(out)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), intent(out)	rcond,
		real(dp), dimension(*), intent(out)	ferr,
		real(dp), dimension(*), intent(out)	berr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DGESVX: uses the LU factorization to compute the solution to a real system of linear equations A * X = B, where A is an N-by-N matrix and X and B are N-by-NRHS matrices. Error bounds on the solution and a condition estimate are also provided.

Here is the call graph for this function:

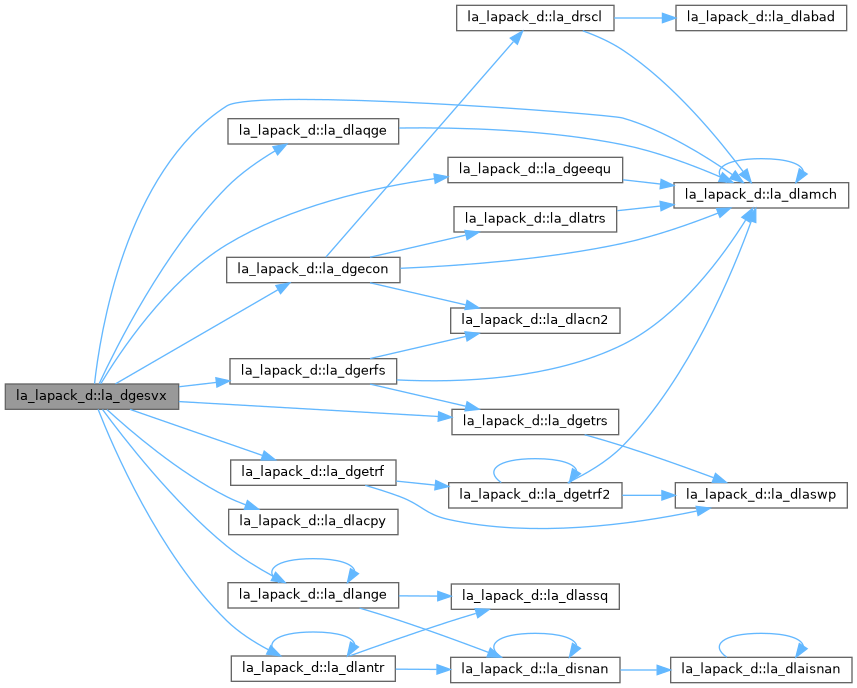
la_dgetc2()

pure subroutine, public la_lapack_d::la_dgetc2	(	integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(out)	ipiv,
		integer(ilp), dimension(*), intent(out)	jpiv,
		integer(ilp), intent(out)	info
	)

DGETC2: computes an LU factorization with complete pivoting of the n-by-n matrix A. The factorization has the form A = P * L * U * Q, where P and Q are permutation matrices, L is lower triangular with unit diagonal elements and U is upper triangular. This is the Level 2 BLAS algorithm.

Here is the call graph for this function:

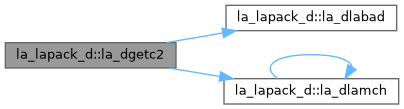
la_dgetf2()

pure subroutine, public la_lapack_d::la_dgetf2	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(out)	ipiv,
		integer(ilp), intent(out)	info
	)

DGETF2: computes an LU factorization of a general m-by-n matrix A using partial pivoting with row interchanges. The factorization has the form A = P * L * U where P is a permutation matrix, L is lower triangular with unit diagonal elements (lower trapezoidal if m > n), and U is upper triangular (upper trapezoidal if m < n). This is the right-looking Level 2 BLAS version of the algorithm.

Here is the call graph for this function:

la_dgetrf()

pure subroutine, public la_lapack_d::la_dgetrf	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(out)	ipiv,
		integer(ilp), intent(out)	info
	)

DGETRF: computes an LU factorization of a general M-by-N matrix A using partial pivoting with row interchanges. The factorization has the form A = P * L * U where P is a permutation matrix, L is lower triangular with unit diagonal elements (lower trapezoidal if m > n), and U is upper triangular (upper trapezoidal if m < n). This is the right-looking Level 3 BLAS version of the algorithm.

Here is the call graph for this function:

la_dgetrf2()

pure recursive subroutine, public la_lapack_d::la_dgetrf2	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(out)	ipiv,
		integer(ilp), intent(out)	info
	)

DGETRF2: computes an LU factorization of a general M-by-N matrix A using partial pivoting with row interchanges. The factorization has the form A = P * L * U where P is a permutation matrix, L is lower triangular with unit diagonal elements (lower trapezoidal if m > n), and U is upper triangular (upper trapezoidal if m < n). This is the recursive version of the algorithm. It divides the matrix into four submatrices: [ A11 | A12 ] where A11 is n1 by n1 and A22 is n2 by n2 A = [ --—|--— ] with n1 = min(m,n)/2 [ A21 | A22 ] n2 = n-n1 [ A11 ] The subroutine calls itself to factor [ — ], [ A12 ] [ A12 ] do the swaps on [ — ], solve A12, update A22, [ A22 ] then calls itself to factor A22 and do the swaps on A21.

Here is the call graph for this function:

la_dgetri()

pure subroutine, public la_lapack_d::la_dgetri	(	integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(in)	ipiv,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGETRI: computes the inverse of a matrix using the LU factorization computed by DGETRF. This method inverts U and then computes inv(A) by solving the system inv(A)*L = inv(U) for inv(A).

Here is the call graph for this function:

la_dgetrs()

pure subroutine, public la_lapack_d::la_dgetrs	(	character, intent(in)	trans,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(in)	ipiv,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	info
	)

DGETRS: solves a system of linear equations A * X = B or A**T * X = B with a general N-by-N matrix A using the LU factorization computed by DGETRF.

Here is the call graph for this function:

la_dgetsls()

subroutine, public la_lapack_d::la_dgetsls	(	character, intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGETSLS: solves overdetermined or underdetermined real linear systems involving an M-by-N matrix A, using a tall skinny QR or short wide LQ factorization of A. It is assumed that A has full rank. The following options are provided:

1. If TRANS = 'N' and m >= n: find the least squares solution of an overdetermined system, i.e., solve the least squares problem minimize || B - A*X ||.
2. If TRANS = 'N' and m < n: find the minimum norm solution of an underdetermined system A * X = B.
3. If TRANS = 'T' and m >= n: find the minimum norm solution of an undetermined system A**T * X = B.
4. If TRANS = 'T' and m < n: find the least squares solution of an overdetermined system, i.e., solve the least squares problem minimize || B - A**T * X ||. Several right hand side vectors b and solution vectors x can be handled in a single call; they are stored as the columns of the M-by-NRHS right hand side matrix B and the N-by-NRHS solution matrix X.

Here is the call graph for this function:

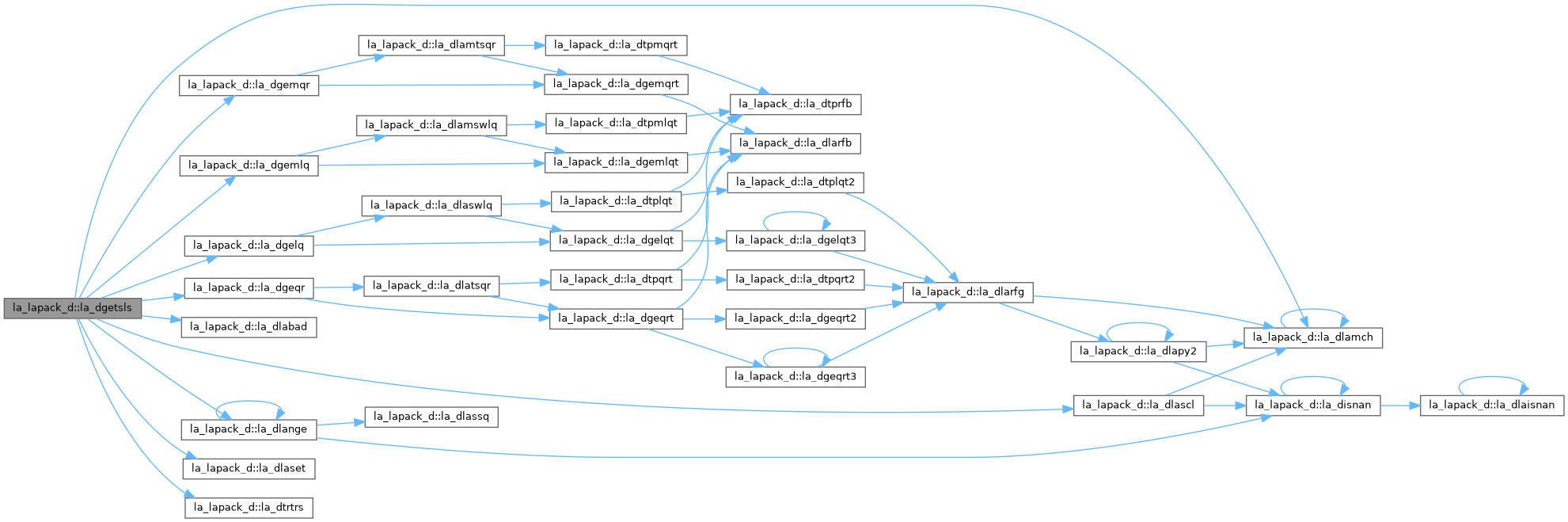
la_dgetsqrhrt()

pure subroutine, public la_lapack_d::la_dgetsqrhrt	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	mb1,
		integer(ilp), intent(in)	nb1,
		integer(ilp), intent(in)	nb2,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldt,*), intent(out)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGETSQRHRT: computes a NB2-sized column blocked QR-factorization of a real M-by-N matrix A with M >= N, A = Q * R. The routine uses internally a NB1-sized column blocked and MB1-sized row blocked TSQR-factorization and perfors the reconstruction of the Householder vectors from the TSQR output. The routine also converts the R_tsqr factor from the TSQR-factorization output into the R factor that corresponds to the Householder QR-factorization, A = Q_tsqr * R_tsqr = Q * R. The output Q and R factors are stored in the same format as in DGEQRT (Q is in blocked compact WY-representation). See the documentation of DGEQRT for more details on the format.

Here is the call graph for this function:

la_dggbak()

pure subroutine, public la_lapack_d::la_dggbak	(	character, intent(in)	job,
		character, intent(in)	side,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ilo,
		integer(ilp), intent(in)	ihi,
		real(dp), dimension(*), intent(in)	lscale,
		real(dp), dimension(*), intent(in)	rscale,
		integer(ilp), intent(in)	m,
		real(dp), dimension(ldv,*), intent(inout)	v,
		integer(ilp), intent(in)	ldv,
		integer(ilp), intent(out)	info
	)

DGGBAK: forms the right or left eigenvectors of a real generalized eigenvalue problem A*x = lambda*B*x, by backward transformation on the computed eigenvectors of the balanced pair of matrices output by DGGBAL.

la_dggbal()

pure subroutine, public la_lapack_d::la_dggbal	(	character, intent(in)	job,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	ilo,
		integer(ilp), intent(out)	ihi,
		real(dp), dimension(*), intent(out)	lscale,
		real(dp), dimension(*), intent(out)	rscale,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DGGBAL: balances a pair of general real matrices (A,B). This involves, first, permuting A and B by similarity transformations to isolate eigenvalues in the first 1 to ILO$-$1 and last IHI+1 to N elements on the diagonal; and second, applying a diagonal similarity transformation to rows and columns ILO to IHI to make the rows and columns as close in norm as possible. Both steps are optional. Balancing may reduce the 1-norm of the matrices, and improve the accuracy of the computed eigenvalues and/or eigenvectors in the generalized eigenvalue problem A*x = lambda*B*x.

Here is the call graph for this function:

la_dgges()

subroutine, public la_lapack_d::la_dgges	(	character, intent(in)	jobvsl,
		character, intent(in)	jobvsr,
		character, intent(in)	sort,
		procedure(la_selctg_d)	selctg,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	sdim,
		real(dp), dimension(*), intent(out)	alphar,
		real(dp), dimension(*), intent(out)	alphai,
		real(dp), dimension(*), intent(out)	beta,
		real(dp), dimension(ldvsl,*), intent(out)	vsl,
		integer(ilp), intent(in)	ldvsl,
		real(dp), dimension(ldvsr,*), intent(out)	vsr,
		integer(ilp), intent(in)	ldvsr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		logical(lk), dimension(*), intent(out)	bwork,
		integer(ilp), intent(out)	info
	)

DGGES: computes for a pair of N-by-N real nonsymmetric matrices (A,B), the generalized eigenvalues, the generalized real Schur form (S,T), optionally, the left and/or right matrices of Schur vectors (VSL and VSR). This gives the generalized Schur factorization (A,B) = ( (VSL)*S*(VSR)**T, (VSL)*T*(VSR)**T ) Optionally, it also orders the eigenvalues so that a selected cluster of eigenvalues appears in the leading diagonal blocks of the upper quasi-triangular matrix S and the upper triangular matrix T.The leading columns of VSL and VSR then form an orthonormal basis for the corresponding left and right eigenspaces (deflating subspaces). (If only the generalized eigenvalues are needed, use the driver DGGEV instead, which is faster.) A generalized eigenvalue for a pair of matrices (A,B) is a scalar w or a ratio alpha/beta = w, such that A - w*B is singular. It is usually represented as the pair (alpha,beta), as there is a reasonable interpretation for beta=0 or both being zero. A pair of matrices (S,T) is in generalized real Schur form if T is upper triangular with non-negative diagonal and S is block upper triangular with 1-by-1 and 2-by-2 blocks. 1-by-1 blocks correspond to real generalized eigenvalues, while 2-by-2 blocks of S will be "standardized" by making the corresponding elements of T have the form: [ a 0 ] [ 0 b ] and the pair of corresponding 2-by-2 blocks in S and T will have a complex conjugate pair of generalized eigenvalues.

Here is the call graph for this function:

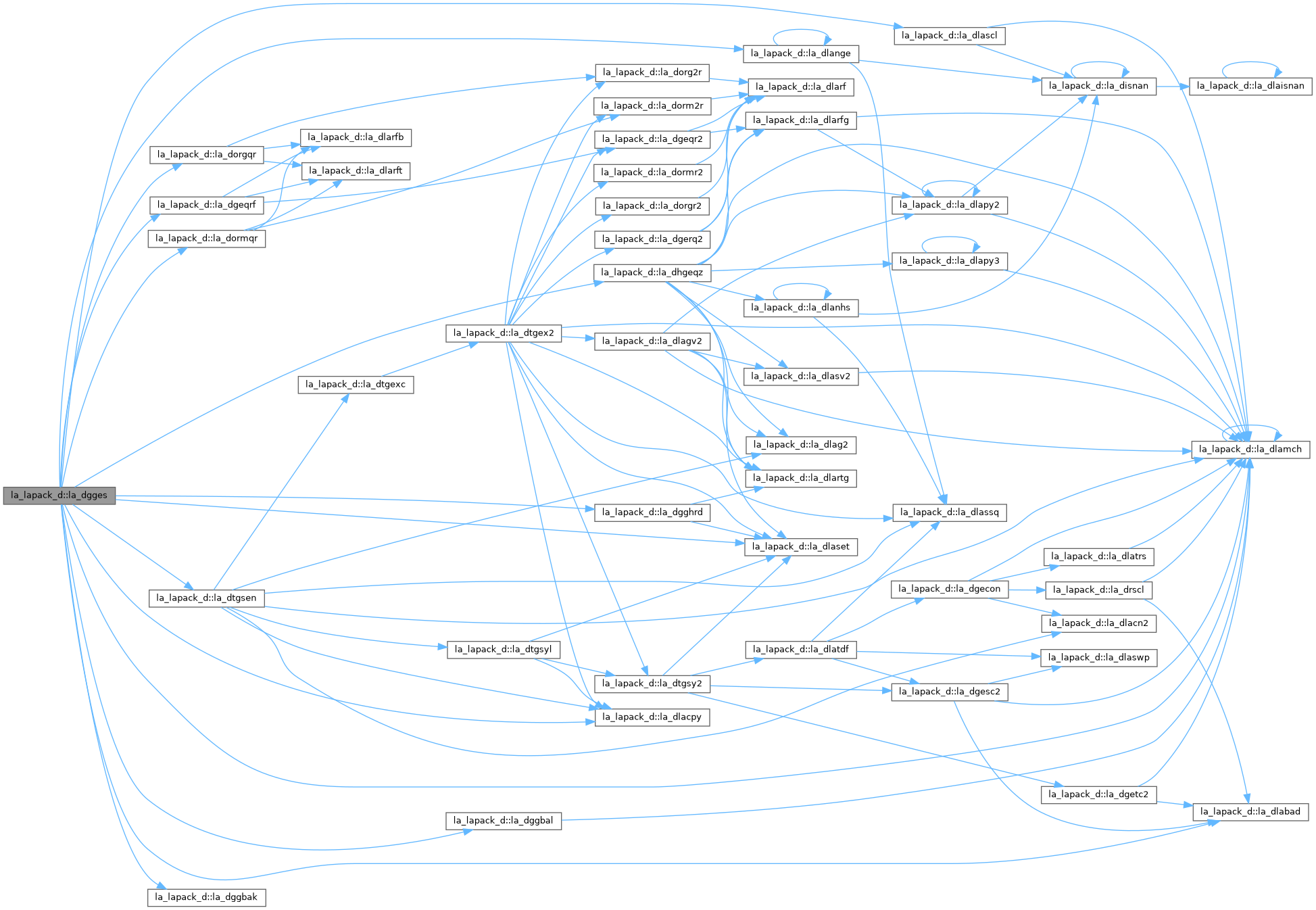
la_dgges3()

subroutine, public la_lapack_d::la_dgges3	(	character, intent(in)	jobvsl,
		character, intent(in)	jobvsr,
		character, intent(in)	sort,
		procedure(la_selctg_d)	selctg,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	sdim,
		real(dp), dimension(*), intent(out)	alphar,
		real(dp), dimension(*), intent(out)	alphai,
		real(dp), dimension(*), intent(out)	beta,
		real(dp), dimension(ldvsl,*), intent(out)	vsl,
		integer(ilp), intent(in)	ldvsl,
		real(dp), dimension(ldvsr,*), intent(out)	vsr,
		integer(ilp), intent(in)	ldvsr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		logical(lk), dimension(*), intent(out)	bwork,
		integer(ilp), intent(out)	info
	)

DGGES3: computes for a pair of N-by-N real nonsymmetric matrices (A,B), the generalized eigenvalues, the generalized real Schur form (S,T), optionally, the left and/or right matrices of Schur vectors (VSL and VSR). This gives the generalized Schur factorization (A,B) = ( (VSL)*S*(VSR)**T, (VSL)*T*(VSR)**T ) Optionally, it also orders the eigenvalues so that a selected cluster of eigenvalues appears in the leading diagonal blocks of the upper quasi-triangular matrix S and the upper triangular matrix T.The leading columns of VSL and VSR then form an orthonormal basis for the corresponding left and right eigenspaces (deflating subspaces). (If only the generalized eigenvalues are needed, use the driver DGGEV instead, which is faster.) A generalized eigenvalue for a pair of matrices (A,B) is a scalar w or a ratio alpha/beta = w, such that A - w*B is singular. It is usually represented as the pair (alpha,beta), as there is a reasonable interpretation for beta=0 or both being zero. A pair of matrices (S,T) is in generalized real Schur form if T is upper triangular with non-negative diagonal and S is block upper triangular with 1-by-1 and 2-by-2 blocks. 1-by-1 blocks correspond to real generalized eigenvalues, while 2-by-2 blocks of S will be "standardized" by making the corresponding elements of T have the form: [ a 0 ] [ 0 b ] and the pair of corresponding 2-by-2 blocks in S and T will have a complex conjugate pair of generalized eigenvalues.

Here is the call graph for this function:

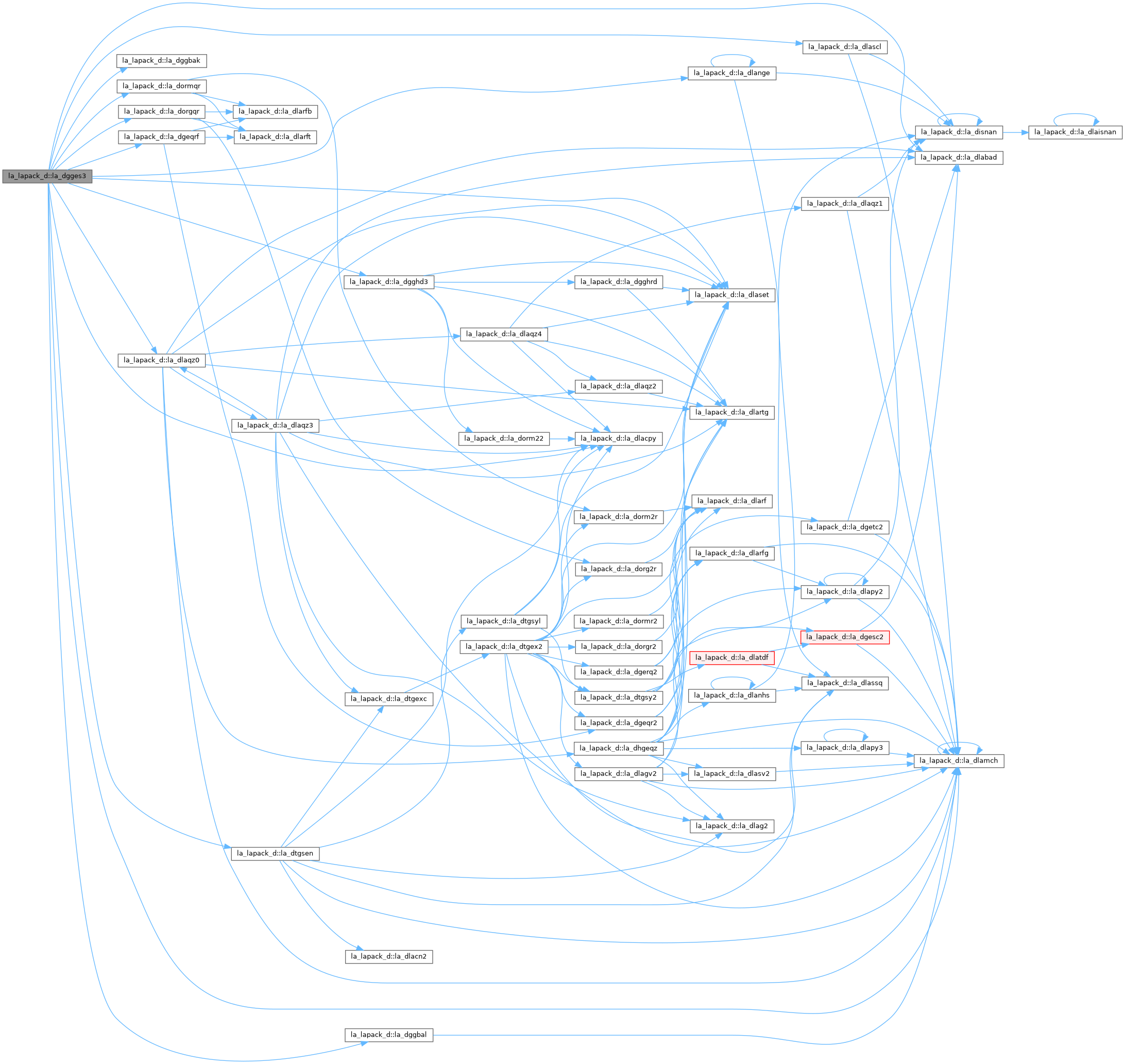
la_dggesx()

subroutine, public la_lapack_d::la_dggesx	(	character, intent(in)	jobvsl,
		character, intent(in)	jobvsr,
		character, intent(in)	sort,
		procedure(la_selctg_d)	selctg,
		character, intent(in)	sense,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	sdim,
		real(dp), dimension(*), intent(out)	alphar,
		real(dp), dimension(*), intent(out)	alphai,
		real(dp), dimension(*), intent(out)	beta,
		real(dp), dimension( ldvsl,*), intent(out)	vsl,
		integer(ilp), intent(in)	ldvsl,
		real(dp), dimension(ldvsr,*), intent(out)	vsr,
		integer(ilp), intent(in)	ldvsr,
		real(dp), dimension(2), intent(out)	rconde,
		real(dp), dimension(2), intent(out)	rcondv,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(in)	liwork,
		logical(lk), dimension(*), intent(out)	bwork,
		integer(ilp), intent(out)	info
	)

DGGESX: computes for a pair of N-by-N real nonsymmetric matrices (A,B), the generalized eigenvalues, the real Schur form (S,T), and, optionally, the left and/or right matrices of Schur vectors (VSL and VSR). This gives the generalized Schur factorization (A,B) = ( (VSL) S (VSR)**T, (VSL) T (VSR)**T ) Optionally, it also orders the eigenvalues so that a selected cluster of eigenvalues appears in the leading diagonal blocks of the upper quasi-triangular matrix S and the upper triangular matrix T; computes a reciprocal condition number for the average of the selected eigenvalues (RCONDE); and computes a reciprocal condition number for the right and left deflating subspaces corresponding to the selected eigenvalues (RCONDV). The leading columns of VSL and VSR then form an orthonormal basis for the corresponding left and right eigenspaces (deflating subspaces). A generalized eigenvalue for a pair of matrices (A,B) is a scalar w or a ratio alpha/beta = w, such that A - w*B is singular. It is usually represented as the pair (alpha,beta), as there is a reasonable interpretation for beta=0 or for both being zero. A pair of matrices (S,T) is in generalized real Schur form if T is upper triangular with non-negative diagonal and S is block upper triangular with 1-by-1 and 2-by-2 blocks. 1-by-1 blocks correspond to real generalized eigenvalues, while 2-by-2 blocks of S will be "standardized" by making the corresponding elements of T have the form: [ a 0 ] [ 0 b ] and the pair of corresponding 2-by-2 blocks in S and T will have a complex conjugate pair of generalized eigenvalues.

Here is the call graph for this function:

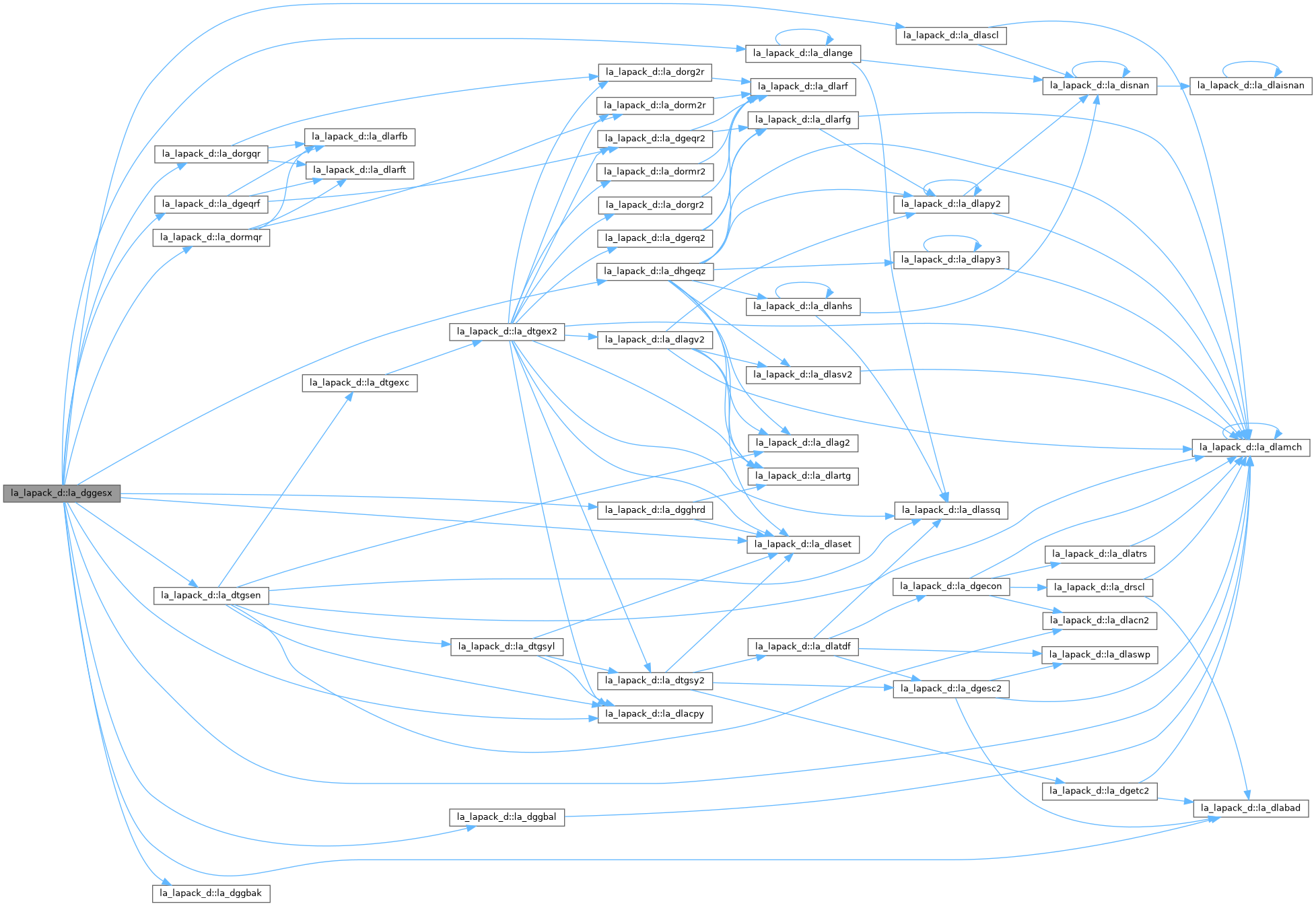
la_dggev()

subroutine, public la_lapack_d::la_dggev	(	character, intent(in)	jobvl,
		character, intent(in)	jobvr,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(*), intent(out)	alphar,
		real(dp), dimension(*), intent(out)	alphai,
		real(dp), dimension(*), intent(out)	beta,
		real(dp), dimension(ldvl,*), intent(out)	vl,
		integer(ilp), intent(in)	ldvl,
		real(dp), dimension(ldvr,*), intent(out)	vr,
		integer(ilp), intent(in)	ldvr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGGEV: computes for a pair of N-by-N real nonsymmetric matrices (A,B) the generalized eigenvalues, and optionally, the left and/or right generalized eigenvectors. A generalized eigenvalue for a pair of matrices (A,B) is a scalar lambda or a ratio alpha/beta = lambda, such that A - lambda*B is singular. It is usually represented as the pair (alpha,beta), as there is a reasonable interpretation for beta=0, and even for both being zero. The right eigenvector v(j) corresponding to the eigenvalue lambda(j) of (A,B) satisfies A * v(j) = lambda(j) * B * v(j). The left eigenvector u(j) corresponding to the eigenvalue lambda(j) of (A,B) satisfies u(j)**H * A = lambda(j) * u(j)**H * B . where u(j)**H is the conjugate-transpose of u(j).

Here is the call graph for this function:

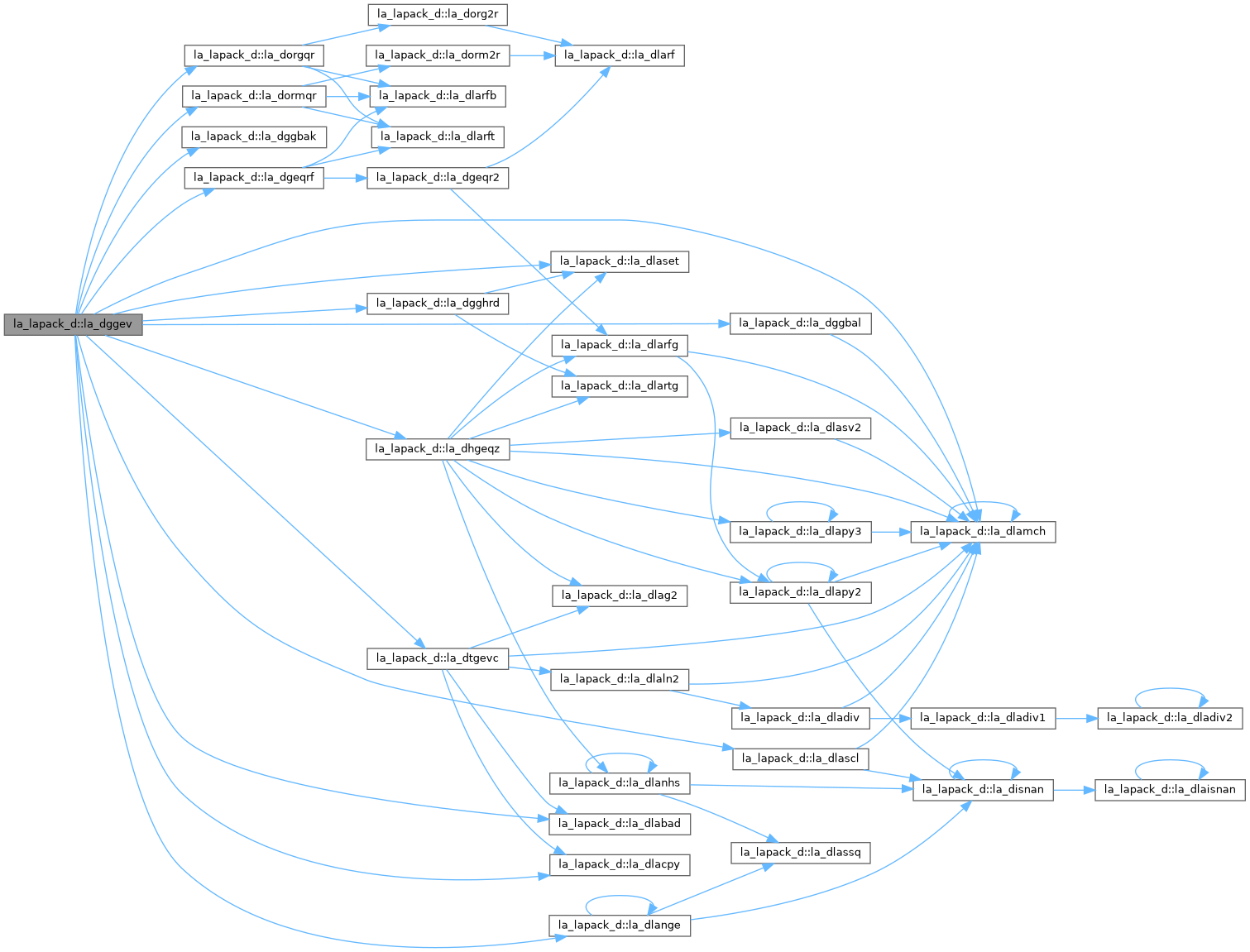
la_dggev3()

subroutine, public la_lapack_d::la_dggev3	(	character, intent(in)	jobvl,
		character, intent(in)	jobvr,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(*), intent(out)	alphar,
		real(dp), dimension(*), intent(out)	alphai,
		real(dp), dimension(*), intent(out)	beta,
		real(dp), dimension(ldvl,*), intent(out)	vl,
		integer(ilp), intent(in)	ldvl,
		real(dp), dimension(ldvr,*), intent(out)	vr,
		integer(ilp), intent(in)	ldvr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGGEV3: computes for a pair of N-by-N real nonsymmetric matrices (A,B) the generalized eigenvalues, and optionally, the left and/or right generalized eigenvectors. A generalized eigenvalue for a pair of matrices (A,B) is a scalar lambda or a ratio alpha/beta = lambda, such that A - lambda*B is singular. It is usually represented as the pair (alpha,beta), as there is a reasonable interpretation for beta=0, and even for both being zero. The right eigenvector v(j) corresponding to the eigenvalue lambda(j) of (A,B) satisfies A * v(j) = lambda(j) * B * v(j). The left eigenvector u(j) corresponding to the eigenvalue lambda(j) of (A,B) satisfies u(j)**H * A = lambda(j) * u(j)**H * B . where u(j)**H is the conjugate-transpose of u(j).

Here is the call graph for this function:

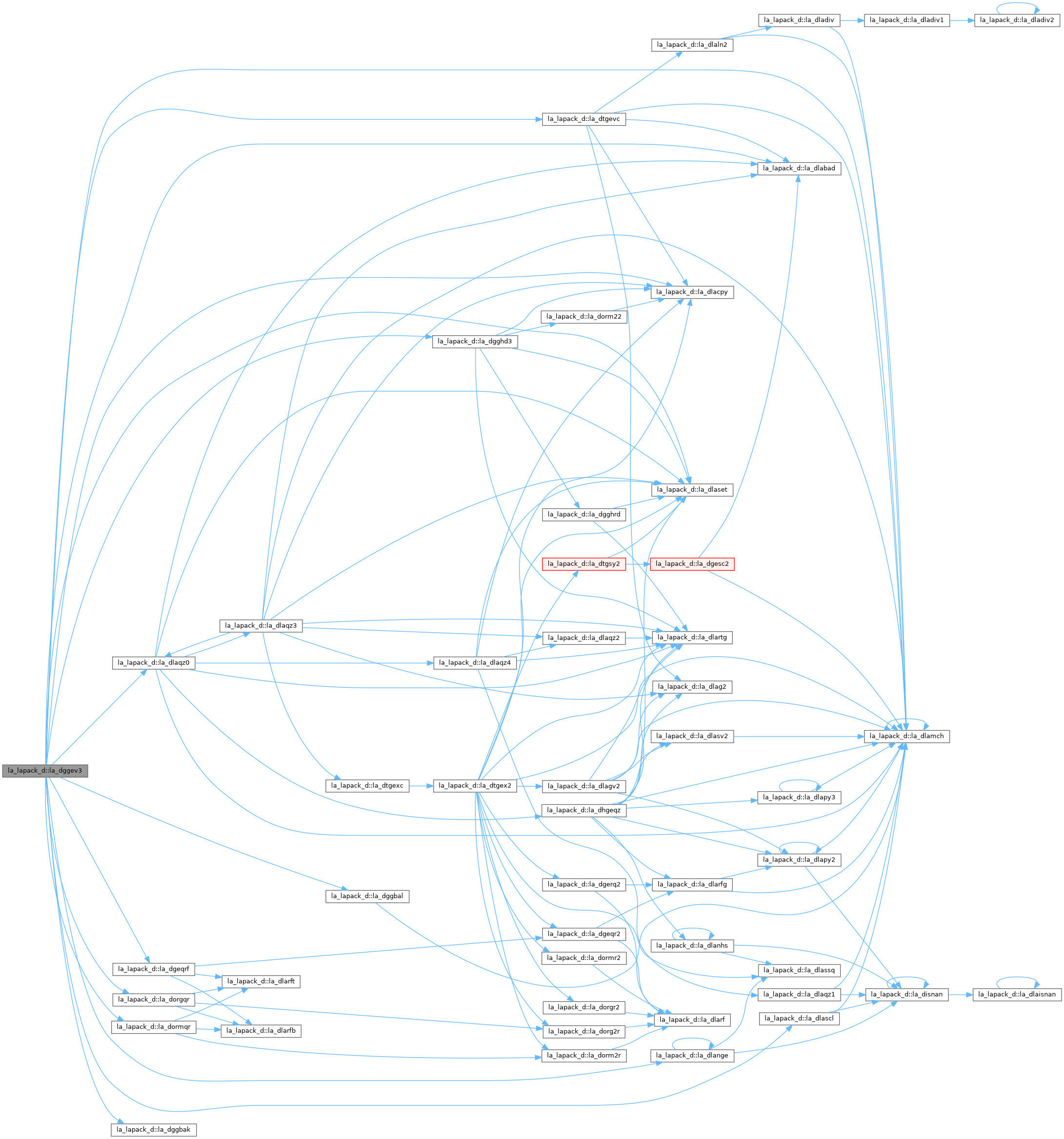
la_dggevx()

subroutine, public la_lapack_d::la_dggevx	(	character, intent(in)	balanc,
		character, intent(in)	jobvl,
		character, intent(in)	jobvr,
		character, intent(in)	sense,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(*), intent(out)	alphar,
		real(dp), dimension(*), intent(out)	alphai,
		real(dp), dimension(*), intent(out)	beta,
		real(dp), dimension(ldvl,*), intent(out)	vl,
		integer(ilp), intent(in)	ldvl,
		real(dp), dimension(ldvr,*), intent(out)	vr,
		integer(ilp), intent(in)	ldvr,
		integer(ilp), intent(out)	ilo,
		integer(ilp), intent(out)	ihi,
		real(dp), dimension(*), intent(out)	lscale,
		real(dp), dimension(*), intent(out)	rscale,
		real(dp), intent(out)	abnrm,
		real(dp), intent(out)	bbnrm,
		real(dp), dimension(*), intent(out)	rconde,
		real(dp), dimension(*), intent(out)	rcondv,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		logical(lk), dimension(*), intent(out)	bwork,
		integer(ilp), intent(out)	info
	)

DGGEVX: computes for a pair of N-by-N real nonsymmetric matrices (A,B) the generalized eigenvalues, and optionally, the left and/or right generalized eigenvectors. Optionally also, it computes a balancing transformation to improve the conditioning of the eigenvalues and eigenvectors (ILO, IHI, LSCALE, RSCALE, ABNRM, and BBNRM), reciprocal condition numbers for the eigenvalues (RCONDE), and reciprocal condition numbers for the right eigenvectors (RCONDV). A generalized eigenvalue for a pair of matrices (A,B) is a scalar lambda or a ratio alpha/beta = lambda, such that A - lambda*B is singular. It is usually represented as the pair (alpha,beta), as there is a reasonable interpretation for beta=0, and even for both being zero. The right eigenvector v(j) corresponding to the eigenvalue lambda(j) of (A,B) satisfies A * v(j) = lambda(j) * B * v(j) . The left eigenvector u(j) corresponding to the eigenvalue lambda(j) of (A,B) satisfies u(j)**H * A = lambda(j) * u(j)**H * B. where u(j)**H is the conjugate-transpose of u(j).

Here is the call graph for this function:

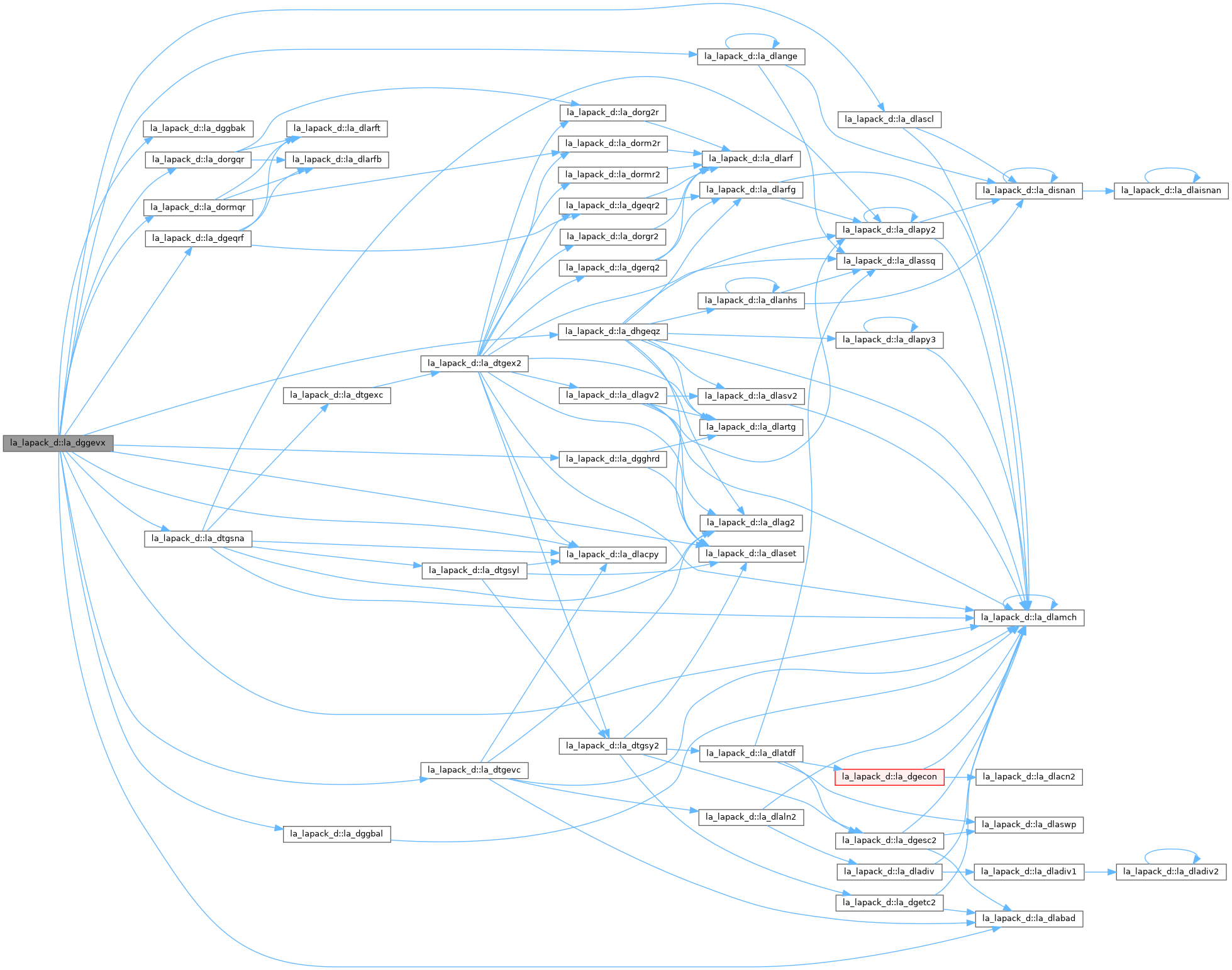
la_dggglm()

pure subroutine, public la_lapack_d::la_dggglm	(	integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	p,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(out)	x,
		real(dp), dimension(*), intent(out)	y,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGGGLM: solves a general Gauss-Markov linear model (GLM) problem: minimize || y ||_2 subject to d = A*x + B*y x where A is an N-by-M matrix, B is an N-by-P matrix, and d is a given N-vector. It is assumed that M <= N <= M+P, and rank(A) = M and rank( A B ) = N. Under these assumptions, the constrained equation is always consistent, and there is a unique solution x and a minimal 2-norm solution y, which is obtained using a generalized QR factorization of the matrices (A, B) given by A = Q*(R), B = Q*T*Z. (0) In particular, if matrix B is square nonsingular, then the problem GLM is equivalent to the following weighted linear least squares problem minimize || inv(B)*(d-A*x) ||_2 x where inv(B) denotes the inverse of B.

Here is the call graph for this function:

la_dgghd3()

pure subroutine, public la_lapack_d::la_dgghd3	(	character, intent(in)	compq,
		character, intent(in)	compz,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ilo,
		integer(ilp), intent(in)	ihi,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldq,*), intent(inout)	q,
		integer(ilp), intent(in)	ldq,
		real(dp), dimension(ldz,*), intent(inout)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGGHD3: reduces a pair of real matrices (A,B) to generalized upper Hessenberg form using orthogonal transformations, where A is a general matrix and B is upper triangular. The form of the generalized eigenvalue problem is A*x = lambda*B*x, and B is typically made upper triangular by computing its QR factorization and moving the orthogonal matrix Q to the left side of the equation. This subroutine simultaneously reduces A to a Hessenberg matrix H: Q**T*A*Z = H and transforms B to another upper triangular matrix T: Q**T*B*Z = T in order to reduce the problem to its standard form H*y = lambda*T*y where y = Z**T*x. The orthogonal matrices Q and Z are determined as products of Givens rotations. They may either be formed explicitly, or they may be postmultiplied into input matrices Q1 and Z1, so that Q1 * A * Z1**T = (Q1*Q) * H * (Z1*Z)**T Q1 * B * Z1**T = (Q1*Q) * T * (Z1*Z)**T If Q1 is the orthogonal matrix from the QR factorization of B in the original equation A*x = lambda*B*x, then DGGHD3 reduces the original problem to generalized Hessenberg form. This is a blocked variant of DGGHRD, using matrix-matrix multiplications for parts of the computation to enhance performance.

Here is the call graph for this function:

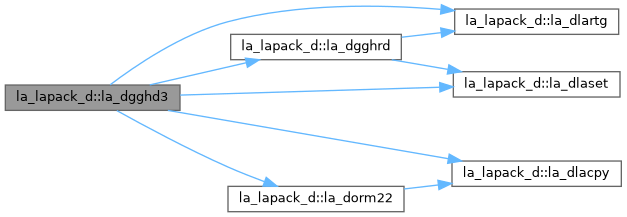
la_dgghrd()

pure subroutine, public la_lapack_d::la_dgghrd	(	character, intent(in)	compq,
		character, intent(in)	compz,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ilo,
		integer(ilp), intent(in)	ihi,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldq,*), intent(inout)	q,
		integer(ilp), intent(in)	ldq,
		real(dp), dimension(ldz,*), intent(inout)	z,
		integer(ilp), intent(in)	ldz,
		integer(ilp), intent(out)	info
	)

DGGHRD: reduces a pair of real matrices (A,B) to generalized upper Hessenberg form using orthogonal transformations, where A is a general matrix and B is upper triangular. The form of the generalized eigenvalue problem is A*x = lambda*B*x, and B is typically made upper triangular by computing its QR factorization and moving the orthogonal matrix Q to the left side of the equation. This subroutine simultaneously reduces A to a Hessenberg matrix H: Q**T*A*Z = H and transforms B to another upper triangular matrix T: Q**T*B*Z = T in order to reduce the problem to its standard form H*y = lambda*T*y where y = Z**T*x. The orthogonal matrices Q and Z are determined as products of Givens rotations. They may either be formed explicitly, or they may be postmultiplied into input matrices Q1 and Z1, so that Q1 * A * Z1**T = (Q1*Q) * H * (Z1*Z)**T Q1 * B * Z1**T = (Q1*Q) * T * (Z1*Z)**T If Q1 is the orthogonal matrix from the QR factorization of B in the original equation A*x = lambda*B*x, then DGGHRD reduces the original problem to generalized Hessenberg form.

Here is the call graph for this function:

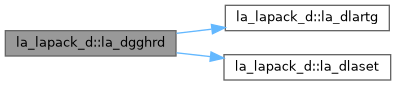
la_dgglse()

pure subroutine, public la_lapack_d::la_dgglse	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	p,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(*), intent(inout)	c,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(out)	x,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGGLSE: solves the linear equality-constrained least squares (LSE) problem: minimize || c - A*x ||_2 subject to B*x = d where A is an M-by-N matrix, B is a P-by-N matrix, c is a given M-vector, and d is a given P-vector. It is assumed that P <= N <= M+P, and rank(B) = P and rank( (A) ) = N. ( (B) ) These conditions ensure that the LSE problem has a unique solution, which is obtained using a generalized RQ factorization of the matrices (B, A) given by B = (0 R)*Q, A = Z*T*Q.

Here is the call graph for this function:

la_dggqrf()

pure subroutine, public la_lapack_d::la_dggqrf	(	integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	p,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	taua,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(*), intent(out)	taub,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGGQRF: computes a generalized QR factorization of an N-by-M matrix A and an N-by-P matrix B: A = Q*R, B = Q*T*Z, where Q is an N-by-N orthogonal matrix, Z is a P-by-P orthogonal matrix, and R and T assume one of the forms: if N >= M, R = ( R11 ) M , or if N < M, R = ( R11 R12 ) N, ( 0 ) N-M N M-N M where R11 is upper triangular, and if N <= P, T = ( 0 T12 ) N, or if N > P, T = ( T11 ) N-P, P-N N ( T21 ) P P where T12 or T21 is upper triangular. In particular, if B is square and nonsingular, the GQR factorization of A and B implicitly gives the QR factorization of inv(B)*A: inv(B)*A = Z**T*(inv(T)*R) where inv(B) denotes the inverse of the matrix B, and Z**T denotes the transpose of the matrix Z.

Here is the call graph for this function:

la_dggrqf()

pure subroutine, public la_lapack_d::la_dggrqf	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	p,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	taua,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(*), intent(out)	taub,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGGRQF: computes a generalized RQ factorization of an M-by-N matrix A and a P-by-N matrix B: A = R*Q, B = Z*T*Q, where Q is an N-by-N orthogonal matrix, Z is a P-by-P orthogonal matrix, and R and T assume one of the forms: if M <= N, R = ( 0 R12 ) M, or if M > N, R = ( R11 ) M-N, N-M M ( R21 ) N N where R12 or R21 is upper triangular, and if P >= N, T = ( T11 ) N , or if P < N, T = ( T11 T12 ) P, ( 0 ) P-N P N-P N where T11 is upper triangular. In particular, if B is square and nonsingular, the GRQ factorization of A and B implicitly gives the RQ factorization of A*inv(B): A*inv(B) = (R*inv(T))*Z**T where inv(B) denotes the inverse of the matrix B, and Z**T denotes the transpose of the matrix Z.

Here is the call graph for this function:

la_dgsvj0()

pure subroutine, public la_lapack_d::la_dgsvj0	(	character, intent(in)	jobv,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(n), intent(inout)	d,
		real(dp), dimension(n), intent(inout)	sva,
		integer(ilp), intent(in)	mv,
		real(dp), dimension(ldv,*), intent(inout)	v,
		integer(ilp), intent(in)	ldv,
		real(dp), intent(in)	eps,
		real(dp), intent(in)	sfmin,
		real(dp), intent(in)	tol,
		integer(ilp), intent(in)	nsweep,
		real(dp), dimension(lwork), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGSVJ0: is called from DGESVJ as a pre-processor and that is its main purpose. It applies Jacobi rotations in the same way as DGESVJ does, but it does not check convergence (stopping criterion). Few tuning parameters (marked by [TP]) are available for the implementer.

Here is the call graph for this function:

la_dgsvj1()

pure subroutine, public la_lapack_d::la_dgsvj1	(	character, intent(in)	jobv,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	n1,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(n), intent(inout)	d,
		real(dp), dimension(n), intent(inout)	sva,
		integer(ilp), intent(in)	mv,
		real(dp), dimension(ldv,*), intent(inout)	v,
		integer(ilp), intent(in)	ldv,
		real(dp), intent(in)	eps,
		real(dp), intent(in)	sfmin,
		real(dp), intent(in)	tol,
		integer(ilp), intent(in)	nsweep,
		real(dp), dimension(lwork), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DGSVJ1: is called from DGESVJ as a pre-processor and that is its main purpose. It applies Jacobi rotations in the same way as DGESVJ does, but it targets only particular pivots and it does not check convergence (stopping criterion). Few tuning parameters (marked by [TP]) are available for the implementer. Further Details ~~~~~~~~~~~~~~~ DGSVJ1 applies few sweeps of Jacobi rotations in the column space of the input M-by-N matrix A. The pivot pairs are taken from the (1,2) off-diagonal block in the corresponding N-by-N Gram matrix A^T * A. The block-entries (tiles) of the (1,2) off-diagonal block are marked by the [x]'s in the following scheme: | * * * [x] [x] [x]| | * * * [x] [x] [x]| Row-cycling in the nblr-by-nblc [x] blocks. | * * * [x] [x] [x]| Row-cyclic pivoting inside each [x] block. |[x] [x] [x] * * * | |[x] [x] [x] * * * | |[x] [x] [x] * * * | In terms of the columns of A, the first N1 columns are rotated 'against' the remaining N-N1 columns, trying to increase the angle between the corresponding subspaces. The off-diagonal block is N1-by(N-N1) and it is tiled using quadratic tiles of side KBL. Here, KBL is a tuning parameter. The number of sweeps is given in NSWEEP and the orthogonality threshold is given in TOL.

Here is the call graph for this function:

la_dgtcon()

pure subroutine, public la_lapack_d::la_dgtcon	(	character, intent(in)	norm,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(in)	dl,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(in)	du,
		real(dp), dimension(*), intent(in)	du2,
		integer(ilp), dimension(*), intent(in)	ipiv,
		real(dp), intent(in)	anorm,
		real(dp), intent(out)	rcond,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DGTCON: estimates the reciprocal of the condition number of a real tridiagonal matrix A using the LU factorization as computed by DGTTRF. An estimate is obtained for norm(inv(A)), and the reciprocal of the condition number is computed as RCOND = 1 / (ANORM * norm(inv(A))).

Here is the call graph for this function:

la_dgtrfs()

pure subroutine, public la_lapack_d::la_dgtrfs	(	character, intent(in)	trans,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(*), intent(in)	dl,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(in)	du,
		real(dp), dimension(*), intent(in)	dlf,
		real(dp), dimension(*), intent(in)	df,
		real(dp), dimension(*), intent(in)	duf,
		real(dp), dimension(*), intent(in)	du2,
		integer(ilp), dimension(*), intent(in)	ipiv,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldx,*), intent(inout)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), dimension(*), intent(out)	ferr,
		real(dp), dimension(*), intent(out)	berr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DGTRFS: improves the computed solution to a system of linear equations when the coefficient matrix is tridiagonal, and provides error bounds and backward error estimates for the solution.

Here is the call graph for this function:

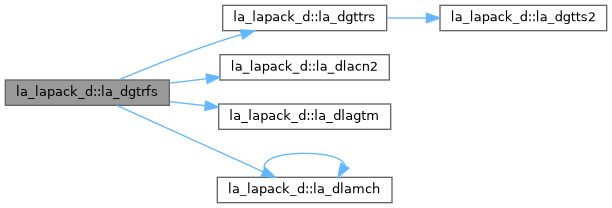
la_dgtsv()

pure subroutine, public la_lapack_d::la_dgtsv	(	integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(*), intent(inout)	dl,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(inout)	du,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	info
	)

DGTSV: solves the equation A*X = B, where A is an n by n tridiagonal matrix, by Gaussian elimination with partial pivoting. Note that the equation A**T*X = B may be solved by interchanging the order of the arguments DU and DL.

la_dgtsvx()

pure subroutine, public la_lapack_d::la_dgtsvx	(	character, intent(in)	fact,
		character, intent(in)	trans,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(*), intent(in)	dl,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(in)	du,
		real(dp), dimension(*), intent(inout)	dlf,
		real(dp), dimension(*), intent(inout)	df,
		real(dp), dimension(*), intent(inout)	duf,
		real(dp), dimension(*), intent(inout)	du2,
		integer(ilp), dimension(*), intent(inout)	ipiv,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldx,*), intent(out)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), intent(out)	rcond,
		real(dp), dimension(*), intent(out)	ferr,
		real(dp), dimension(*), intent(out)	berr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DGTSVX: uses the LU factorization to compute the solution to a real system of linear equations A * X = B or A**T * X = B, where A is a tridiagonal matrix of order N and X and B are N-by-NRHS matrices. Error bounds on the solution and a condition estimate are also provided.

Here is the call graph for this function:

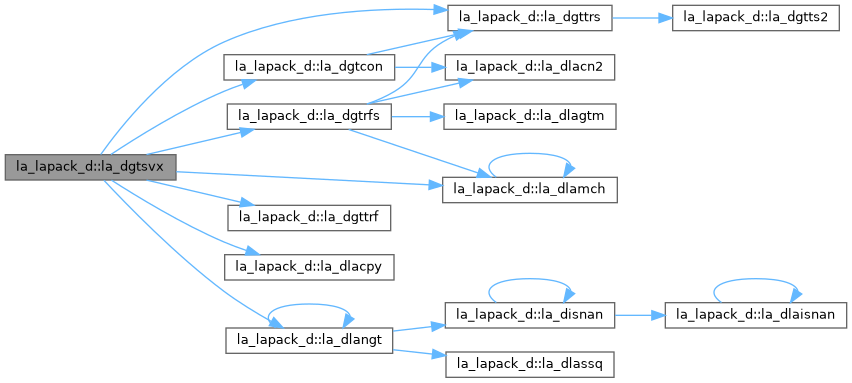
la_dgttrf()

pure subroutine, public la_lapack_d::la_dgttrf	(	integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	dl,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(inout)	du,
		real(dp), dimension(*), intent(out)	du2,
		integer(ilp), dimension(*), intent(out)	ipiv,
		integer(ilp), intent(out)	info
	)

DGTTRF: computes an LU factorization of a real tridiagonal matrix A using elimination with partial pivoting and row interchanges. The factorization has the form A = L * U where L is a product of permutation and unit lower bidiagonal matrices and U is upper triangular with nonzeros in only the main diagonal and first two superdiagonals.

la_dgttrs()

pure subroutine, public la_lapack_d::la_dgttrs	(	character, intent(in)	trans,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(*), intent(in)	dl,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(in)	du,
		real(dp), dimension(*), intent(in)	du2,
		integer(ilp), dimension(*), intent(in)	ipiv,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	info
	)

DGTTRS: solves one of the systems of equations A*X = B or A**T*X = B, with a tridiagonal matrix A using the LU factorization computed by DGTTRF.

Here is the call graph for this function:

la_dgtts2()

pure subroutine, public la_lapack_d::la_dgtts2	(	integer(ilp), intent(in)	itrans,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(*), intent(in)	dl,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(in)	du,
		real(dp), dimension(*), intent(in)	du2,
		integer(ilp), dimension(*), intent(in)	ipiv,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb
	)

DGTTS2: solves one of the systems of equations A*X = B or A**T*X = B, with a tridiagonal matrix A using the LU factorization computed by DGTTRF.

la_dhgeqz()

subroutine, public la_lapack_d::la_dhgeqz	(	character, intent(in)	job,
		character, intent(in)	compq,
		character, intent(in)	compz,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ilo,
		integer(ilp), intent(in)	ihi,
		real(dp), dimension(ldh,*), intent(inout)	h,
		integer(ilp), intent(in)	ldh,
		real(dp), dimension(ldt,*), intent(inout)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(*), intent(out)	alphar,
		real(dp), dimension(*), intent(out)	alphai,
		real(dp), dimension(*), intent(out)	beta,
		real(dp), dimension(ldq,*), intent(inout)	q,
		integer(ilp), intent(in)	ldq,
		real(dp), dimension(ldz,*), intent(inout)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DHGEQZ: computes the eigenvalues of a real matrix pair (H,T), where H is an upper Hessenberg matrix and T is upper triangular, using the double-shift QZ method. Matrix pairs of this type are produced by the reduction to generalized upper Hessenberg form of a real matrix pair (A,B): A = Q1*H*Z1**T, B = Q1*T*Z1**T, as computed by DGGHRD. If JOB='S', then the Hessenberg-triangular pair (H,T) is also reduced to generalized Schur form, H = Q*S*Z**T, T = Q*P*Z**T, where Q and Z are orthogonal matrices, P is an upper triangular matrix, and S is a quasi-triangular matrix with 1-by-1 and 2-by-2 diagonal blocks. The 1-by-1 blocks correspond to real eigenvalues of the matrix pair (H,T) and the 2-by-2 blocks correspond to complex conjugate pairs of eigenvalues. Additionally, the 2-by-2 upper triangular diagonal blocks of P corresponding to 2-by-2 blocks of S are reduced to positive diagonal form, i.e., if S(j+1,j) is non-zero, then P(j+1,j) = P(j,j+1) = 0, P(j,j) > 0, and P(j+1,j+1) > 0. Optionally, the orthogonal matrix Q from the generalized Schur factorization may be postmultiplied into an input matrix Q1, and the orthogonal matrix Z may be postmultiplied into an input matrix Z1. If Q1 and Z1 are the orthogonal matrices from DGGHRD that reduced the matrix pair (A,B) to generalized upper Hessenberg form, then the output matrices Q1*Q and Z1*Z are the orthogonal factors from the generalized Schur factorization of (A,B): A = (Q1*Q)*S*(Z1*Z)**T, B = (Q1*Q)*P*(Z1*Z)**T. To avoid overflow, eigenvalues of the matrix pair (H,T) (equivalently, of (A,B)) are computed as a pair of values (alpha,beta), where alpha is complex and beta real. If beta is nonzero, lambda = alpha / beta is an eigenvalue of the generalized nonsymmetric eigenvalue problem (GNEP) A*x = lambda*B*x and if alpha is nonzero, mu = beta / alpha is an eigenvalue of the alternate form of the GNEP mu*A*y = B*y. Real eigenvalues can be read directly from the generalized Schur form: alpha = S(i,i), beta = P(i,i). Ref: C.B. Moler Eigenvalue Problems", SIAM J. Numer. Anal., 10(1973), pp. 241–256.

Here is the call graph for this function:

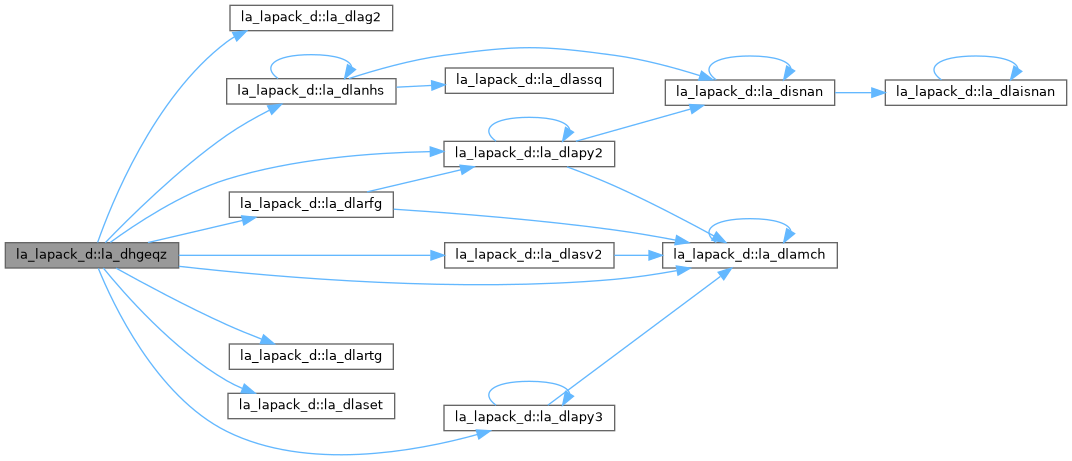
la_dhsein()

subroutine, public la_lapack_d::la_dhsein	(	character, intent(in)	side,
		character, intent(in)	eigsrc,
		character, intent(in)	initv,
		logical(lk), dimension(*), intent(inout)	select,
		integer(ilp), intent(in)	n,
		real(dp), dimension(ldh,*), intent(in)	h,
		integer(ilp), intent(in)	ldh,
		real(dp), dimension(*), intent(inout)	wr,
		real(dp), dimension(*), intent(in)	wi,
		real(dp), dimension(ldvl,*), intent(inout)	vl,
		integer(ilp), intent(in)	ldvl,
		real(dp), dimension(ldvr,*), intent(inout)	vr,
		integer(ilp), intent(in)	ldvr,
		integer(ilp), intent(in)	mm,
		integer(ilp), intent(out)	m,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	ifaill,
		integer(ilp), dimension(*), intent(out)	ifailr,
		integer(ilp), intent(out)	info
	)

DHSEIN: uses inverse iteration to find specified right and/or left eigenvectors of a real upper Hessenberg matrix H. The right eigenvector x and the left eigenvector y of the matrix H corresponding to an eigenvalue w are defined by: H * x = w * x, y**h * H = w * y**h where y**h denotes the conjugate transpose of the vector y.

Here is the call graph for this function:

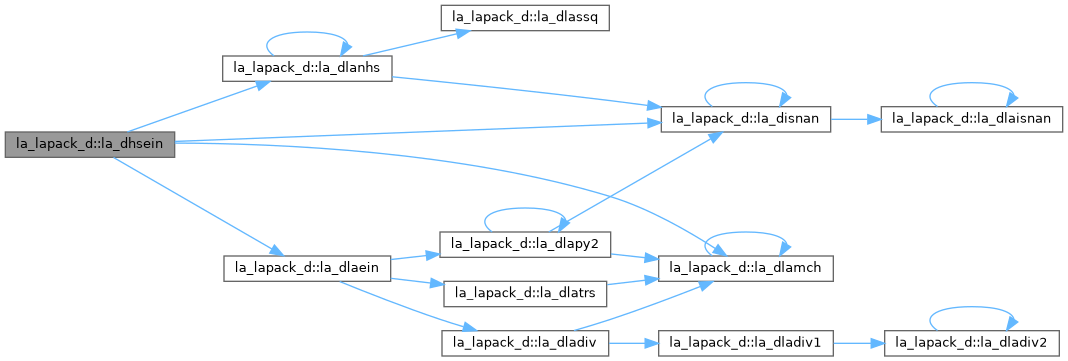
la_dhseqr()

subroutine, public la_lapack_d::la_dhseqr	(	character, intent(in)	job,
		character, intent(in)	compz,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ilo,
		integer(ilp), intent(in)	ihi,
		real(dp), dimension(ldh,*), intent(inout)	h,
		integer(ilp), intent(in)	ldh,
		real(dp), dimension(*), intent(out)	wr,
		real(dp), dimension(*), intent(out)	wi,
		real(dp), dimension(ldz,*), intent(inout)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DHSEQR: computes the eigenvalues of a Hessenberg matrix H and, optionally, the matrices T and Z from the Schur decomposition H = Z T Z**T, where T is an upper quasi-triangular matrix (the Schur form), and Z is the orthogonal matrix of Schur vectors. Optionally Z may be postmultiplied into an input orthogonal matrix Q so that this routine can give the Schur factorization of a matrix A which has been reduced to the Hessenberg form H by the orthogonal matrix Q: A = Q*H*Q**T = (QZ)*T*(QZ)**T.

Here is the call graph for this function:

la_disnan()

pure logical(lk) function, public la_lapack_d::la_disnan

(

real(dp), intent(in)

din

)

DISNAN: returns .TRUE. if its argument is NaN, and .FALSE. otherwise. To be replaced by the Fortran 2003 intrinsic in the future.

Here is the call graph for this function:

la_dla_gbamv()

subroutine, public la_lapack_d::la_dla_gbamv	(	integer(ilp), intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kl,
		integer(ilp), intent(in)	ku,
		real(dp), intent(in)	alpha,
		real(dp), dimension(ldab,*), intent(in)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(*), intent(in)	x,
		integer(ilp), intent(in)	incx,
		real(dp), intent(in)	beta,
		real(dp), dimension(*), intent(inout)	y,
		integer(ilp), intent(in)	incy
	)

DLA_GBAMV: performs one of the matrix-vector operations y := alpha*abs(A)*abs(x) + beta*abs(y), or y := alpha*abs(A)**T*abs(x) + beta*abs(y), where alpha and beta are scalars, x and y are vectors and A is an m by n matrix. This function is primarily used in calculating error bounds. To protect against underflow during evaluation, components in the resulting vector are perturbed away from zero by (N+1) times the underflow threshold. To prevent unnecessarily large errors for block-structure embedded in general matrices, "symbolically" zero components are not perturbed. A zero entry is considered "symbolic" if all multiplications involved in computing that entry have at least one zero multiplicand.

Here is the call graph for this function:

la_dla_gbrcond()

real(dp) function, public la_lapack_d::la_dla_gbrcond	(	character, intent(in)	trans,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kl,
		integer(ilp), intent(in)	ku,
		real(dp), dimension(ldab,*), intent(in)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(ldafb,*), intent(in)	afb,
		integer(ilp), intent(in)	ldafb,
		integer(ilp), dimension(*), intent(in)	ipiv,
		integer(ilp), intent(in)	cmode,
		real(dp), dimension(*), intent(in)	c,
		integer(ilp), intent(out)	info,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork
	)

DLA_GBRCOND: Estimates the Skeel condition number of op(A) * op2(C) where op2 is determined by CMODE as follows CMODE = 1 op2(C) = C CMODE = 0 op2(C) = I CMODE = -1 op2(C) = inv(C) The Skeel condition number cond(A) = norminf( |inv(A)||A| ) is computed by computing scaling factors R such that diag(R)*A*op2(C) is row equilibrated and computing the standard infinity-norm condition number.

Here is the call graph for this function:

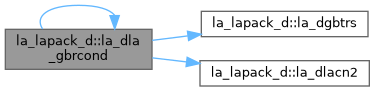
la_dla_gbrpvgrw()

pure real(dp) function, public la_lapack_d::la_dla_gbrpvgrw	(	integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kl,
		integer(ilp), intent(in)	ku,
		integer(ilp), intent(in)	ncols,
		real(dp), dimension(ldab,*), intent(in)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(ldafb,*), intent(in)	afb,
		integer(ilp), intent(in)	ldafb
	)

DLA_GBRPVGRW: computes the reciprocal pivot growth factor norm(A)/norm(U). The "max absolute element" norm is used. If this is much less than 1, the stability of the LU factorization of the (equilibrated) matrix A could be poor. This also means that the solution X, estimated condition numbers, and error bounds could be unreliable.

Here is the call graph for this function:

la_dla_geamv()

subroutine, public la_lapack_d::la_dla_geamv	(	integer(ilp), intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), intent(in)	alpha,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	x,
		integer(ilp), intent(in)	incx,
		real(dp), intent(in)	beta,
		real(dp), dimension(*), intent(inout)	y,
		integer(ilp), intent(in)	incy
	)

DLA_GEAMV: performs one of the matrix-vector operations y := alpha*abs(A)*abs(x) + beta*abs(y), or y := alpha*abs(A)**T*abs(x) + beta*abs(y), where alpha and beta are scalars, x and y are vectors and A is an m by n matrix. This function is primarily used in calculating error bounds. To protect against underflow during evaluation, components in the resulting vector are perturbed away from zero by (N+1) times the underflow threshold. To prevent unnecessarily large errors for block-structure embedded in general matrices, "symbolically" zero components are not perturbed. A zero entry is considered "symbolic" if all multiplications involved in computing that entry have at least one zero multiplicand.

Here is the call graph for this function:

la_dla_gercond()

real(dp) function, public la_lapack_d::la_dla_gercond	(	character, intent(in)	trans,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldaf,*), intent(in)	af,
		integer(ilp), intent(in)	ldaf,
		integer(ilp), dimension(*), intent(in)	ipiv,
		integer(ilp), intent(in)	cmode,
		real(dp), dimension(*), intent(in)	c,
		integer(ilp), intent(out)	info,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork
	)

DLA_GERCOND: estimates the Skeel condition number of op(A) * op2(C) where op2 is determined by CMODE as follows CMODE = 1 op2(C) = C CMODE = 0 op2(C) = I CMODE = -1 op2(C) = inv(C) The Skeel condition number cond(A) = norminf( |inv(A)||A| ) is computed by computing scaling factors R such that diag(R)*A*op2(C) is row equilibrated and computing the standard infinity-norm condition number.

Here is the call graph for this function:

la_dla_gerpvgrw()

pure real(dp) function, public la_lapack_d::la_dla_gerpvgrw	(	integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ncols,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldaf,*), intent(in)	af,
		integer(ilp), intent(in)	ldaf
	)

DLA_GERPVGRW: computes the reciprocal pivot growth factor norm(A)/norm(U). The "max absolute element" norm is used. If this is much less than 1, the stability of the LU factorization of the (equilibrated) matrix A could be poor. This also means that the solution X, estimated condition numbers, and error bounds could be unreliable.

Here is the call graph for this function:

la_dla_lin_berr()

pure subroutine, public la_lapack_d::la_dla_lin_berr	(	integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nz,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(n,nrhs), intent(in)	res,
		real(dp), dimension(n,nrhs), intent(in)	ayb,
		real(dp), dimension(nrhs), intent(out)	berr
	)

DLA_LIN_BERR: computes component-wise relative backward error from the formula max(i) ( abs(R(i)) / ( abs(op(A_s))*abs(Y) + abs(B_s) )(i) ) where abs(Z) is the component-wise absolute value of the matrix or vector Z.

Here is the call graph for this function:

la_dla_porcond()

real(dp) function, public la_lapack_d::la_dla_porcond	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldaf,*), intent(in)	af,
		integer(ilp), intent(in)	ldaf,
		integer(ilp), intent(in)	cmode,
		real(dp), dimension(*), intent(in)	c,
		integer(ilp), intent(out)	info,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork
	)

DLA_PORCOND: Estimates the Skeel condition number of op(A) * op2(C) where op2 is determined by CMODE as follows CMODE = 1 op2(C) = C CMODE = 0 op2(C) = I CMODE = -1 op2(C) = inv(C) The Skeel condition number cond(A) = norminf( |inv(A)||A| ) is computed by computing scaling factors R such that diag(R)*A*op2(C) is row equilibrated and computing the standard infinity-norm condition number.

Here is the call graph for this function:

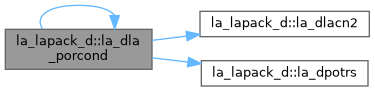
la_dla_porpvgrw()

real(dp) function, public la_lapack_d::la_dla_porpvgrw	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	ncols,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldaf,*), intent(in)	af,
		integer(ilp), intent(in)	ldaf,
		real(dp), dimension(*), intent(out)	work
	)

DLA_PORPVGRW: computes the reciprocal pivot growth factor norm(A)/norm(U). The "max absolute element" norm is used. If this is much less than 1, the stability of the LU factorization of the (equilibrated) matrix A could be poor. This also means that the solution X, estimated condition numbers, and error bounds could be unreliable.

Here is the call graph for this function:

la_dla_syamv()

subroutine, public la_lapack_d::la_dla_syamv	(	integer(ilp), intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), intent(in)	alpha,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	x,
		integer(ilp), intent(in)	incx,
		real(dp), intent(in)	beta,
		real(dp), dimension(*), intent(inout)	y,
		integer(ilp), intent(in)	incy
	)

DLA_SYAMV: performs the matrix-vector operation y := alpha*abs(A)*abs(x) + beta*abs(y), where alpha and beta are scalars, x and y are vectors and A is an n by n symmetric matrix. This function is primarily used in calculating error bounds. To protect against underflow during evaluation, components in the resulting vector are perturbed away from zero by (N+1) times the underflow threshold. To prevent unnecessarily large errors for block-structure embedded in general matrices, "symbolically" zero components are not perturbed. A zero entry is considered "symbolic" if all multiplications involved in computing that entry have at least one zero multiplicand.

Here is the call graph for this function:

la_dla_syrcond()

real(dp) function, public la_lapack_d::la_dla_syrcond	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldaf,*), intent(in)	af,
		integer(ilp), intent(in)	ldaf,
		integer(ilp), dimension(*), intent(in)	ipiv,
		integer(ilp), intent(in)	cmode,
		real(dp), dimension(*), intent(in)	c,
		integer(ilp), intent(out)	info,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork
	)

DLA_SYRCOND: estimates the Skeel condition number of op(A) * op2(C) where op2 is determined by CMODE as follows CMODE = 1 op2(C) = C CMODE = 0 op2(C) = I CMODE = -1 op2(C) = inv(C) The Skeel condition number cond(A) = norminf( |inv(A)||A| ) is computed by computing scaling factors R such that diag(R)*A*op2(C) is row equilibrated and computing the standard infinity-norm condition number.

Here is the call graph for this function:

la_dla_syrpvgrw()

real(dp) function, public la_lapack_d::la_dla_syrpvgrw	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	info,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldaf,*), intent(in)	af,
		integer(ilp), intent(in)	ldaf,
		integer(ilp), dimension(*), intent(in)	ipiv,
		real(dp), dimension(*), intent(out)	work
	)

DLA_SYRPVGRW: computes the reciprocal pivot growth factor norm(A)/norm(U). The "max absolute element" norm is used. If this is much less than 1, the stability of the LU factorization of the (equilibrated) matrix A could be poor. This also means that the solution X, estimated condition numbers, and error bounds could be unreliable.

Here is the call graph for this function:

la_dla_wwaddw()

pure subroutine, public la_lapack_d::la_dla_wwaddw	(	integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	x,
		real(dp), dimension(*), intent(inout)	y,
		real(dp), dimension(*), intent(in)	w
	)

DLA_WWADDW: adds a vector W into a doubled-single vector (X, Y). This works for all extant IBM's hex and binary floating point arithmetic, but not for decimal.

la_dlabad()

pure subroutine, public la_lapack_d::la_dlabad	(	real(dp), intent(inout)	small,
		real(dp), intent(inout)	large
	)

DLABAD: takes as input the values computed by DLAMCH for underflow and overflow, and returns the square root of each of these values if the log of LARGE is sufficiently large. This subroutine is intended to identify machines with a large exponent range, such as the Crays, and redefine the underflow and overflow limits to be the square roots of the values computed by DLAMCH. This subroutine is needed because DLAMCH does not compensate for poor arithmetic in the upper half of the exponent range, as is found on a Cray.

la_dlabrd()

pure subroutine, public la_lapack_d::la_dlabrd	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nb,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	d,
		real(dp), dimension(*), intent(out)	e,
		real(dp), dimension(*), intent(out)	tauq,
		real(dp), dimension(*), intent(out)	taup,
		real(dp), dimension(ldx,*), intent(out)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), dimension(ldy,*), intent(out)	y,
		integer(ilp), intent(in)	ldy
	)

DLABRD: reduces the first NB rows and columns of a real general m by n matrix A to upper or lower bidiagonal form by an orthogonal transformation Q**T * A * P, and returns the matrices X and Y which are needed to apply the transformation to the unreduced part of A. If m >= n, A is reduced to upper bidiagonal form; if m < n, to lower bidiagonal form. This is an auxiliary routine called by DGEBRD.

Here is the call graph for this function:

la_dlacn2()

pure subroutine, public la_lapack_d::la_dlacn2	(	integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(out)	v,
		real(dp), dimension(*), intent(inout)	x,
		integer(ilp), dimension(*), intent(out)	isgn,
		real(dp), intent(inout)	est,
		integer(ilp), intent(inout)	kase,
		integer(ilp), dimension(3), intent(inout)	isave
	)

DLACN2: estimates the 1-norm of a square, real matrix A. Reverse communication is used for evaluating matrix-vector products.

la_dlacon()

subroutine, public la_lapack_d::la_dlacon	(	integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(out)	v,
		real(dp), dimension(*), intent(inout)	x,
		integer(ilp), dimension(*), intent(out)	isgn,
		real(dp), intent(inout)	est,
		integer(ilp), intent(inout)	kase
	)

DLACON: estimates the 1-norm of a square, real matrix A. Reverse communication is used for evaluating matrix-vector products.

la_dlacpy()

pure subroutine, public la_lapack_d::la_dlacpy	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(out)	b,
		integer(ilp), intent(in)	ldb
	)

DLACPY: copies all or part of a two-dimensional matrix A to another matrix B.

la_dladiv()

pure subroutine, public la_lapack_d::la_dladiv	(	real(dp), intent(in)	a,
		real(dp), intent(in)	b,
		real(dp), intent(in)	c,
		real(dp), intent(in)	d,
		real(dp), intent(out)	p,
		real(dp), intent(out)	q
	)

DLADIV: performs complex division in real arithmetic a + i*b p + i*q = ------— c + i*d The algorithm is due to Michael Baudin and Robert L. Smith and can be found in the paper "A Robust Complex Division in Scilab".

Here is the call graph for this function:

la_dladiv1()

pure subroutine, public la_lapack_d::la_dladiv1	(	real(dp), intent(inout)	a,
		real(dp), intent(in)	b,
		real(dp), intent(in)	c,
		real(dp), intent(in)	d,
		real(dp), intent(out)	p,
		real(dp), intent(out)	q
	)

Here is the call graph for this function:

la_dladiv2()

pure real(dp) function, public la_lapack_d::la_dladiv2	(	real(dp), intent(in)	a,
		real(dp), intent(in)	b,
		real(dp), intent(in)	c,
		real(dp), intent(in)	d,
		real(dp), intent(in)	r,
		real(dp), intent(in)	t
	)

Here is the call graph for this function:

la_dlae2()

pure subroutine, public la_lapack_d::la_dlae2	(	real(dp), intent(in)	a,
		real(dp), intent(in)	b,
		real(dp), intent(in)	c,
		real(dp), intent(out)	rt1,
		real(dp), intent(out)	rt2
	)

DLAE2: computes the eigenvalues of a 2-by-2 symmetric matrix [ A B ] [ B C ]. On return, RT1 is the eigenvalue of larger absolute value, and RT2 is the eigenvalue of smaller absolute value.

la_dlaebz()

pure subroutine, public la_lapack_d::la_dlaebz	(	integer(ilp), intent(in)	ijob,
		integer(ilp), intent(in)	nitmax,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	mmax,
		integer(ilp), intent(in)	minp,
		integer(ilp), intent(in)	nbmin,
		real(dp), intent(in)	abstol,
		real(dp), intent(in)	reltol,
		real(dp), intent(in)	pivmin,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(in)	e,
		real(dp), dimension(*), intent(in)	e2,
		integer(ilp), dimension(*), intent(inout)	nval,
		real(dp), dimension(mmax,*), intent(inout)	ab,
		real(dp), dimension(*), intent(inout)	c,
		integer(ilp), intent(out)	mout,
		integer(ilp), dimension(mmax,*), intent(inout)	nab,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DLAEBZ: contains the iteration loops which compute and use the function N(w), which is the count of eigenvalues of a symmetric tridiagonal matrix T less than or equal to its argument w. It performs a choice of two types of loops: IJOB=1, followed by IJOB=2: It takes as input a list of intervals and returns a list of sufficiently small intervals whose union contains the same eigenvalues as the union of the original intervals. The input intervals are (AB(j,1),AB(j,2)], j=1,...,MINP. The output interval (AB(j,1),AB(j,2)] will contain eigenvalues NAB(j,1)+1,...,NAB(j,2), where 1 <= j <= MOUT. IJOB=3: It performs a binary search in each input interval (AB(j,1),AB(j,2)] for a point w(j) such that N(w(j))=NVAL(j), and uses C(j) as the starting point of the search. If such a w(j) is found, then on output AB(j,1)=AB(j,2)=w. If no such w(j) is found, then on output (AB(j,1),AB(j,2)] will be a small interval containing the point where N(w) jumps through NVAL(j), unless that point lies outside the initial interval. Note that the intervals are in all cases half-open intervals, i.e., of the form (a,b] , which includes b but not a . To avoid underflow, the matrix should be scaled so that its largest element is no greater than overflow**(1/2) * underflow**(1/4) in absolute value. To assure the most accurate computation of small eigenvalues, the matrix should be scaled to be not much smaller than that, either. See W. Kahan "Accurate Eigenvalues of a Symmetric Tridiagonal Matrix", Report CS41, Computer Science Dept., Stanford University, July 21, 1966 Note: the arguments are, in general, not checked for unreasonable values.

la_dlaed0()

pure subroutine, public la_lapack_d::la_dlaed0	(	integer(ilp), intent(in)	icompq,
		integer(ilp), intent(in)	qsiz,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(inout)	e,
		real(dp), dimension(ldq,*), intent(inout)	q,
		integer(ilp), intent(in)	ldq,
		real(dp), dimension(ldqs,*), intent(out)	qstore,
		integer(ilp), intent(in)	ldqs,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DLAED0: computes all eigenvalues and corresponding eigenvectors of a symmetric tridiagonal matrix using the divide and conquer method.

Here is the call graph for this function:

la_dlaed1()

pure subroutine, public la_lapack_d::la_dlaed1	(	integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(ldq,*), intent(inout)	q,
		integer(ilp), intent(in)	ldq,
		integer(ilp), dimension(*), intent(inout)	indxq,
		real(dp), intent(inout)	rho,
		integer(ilp), intent(in)	cutpnt,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DLAED1: computes the updated eigensystem of a diagonal matrix after modification by a rank-one symmetric matrix. This routine is used only for the eigenproblem which requires all eigenvalues and eigenvectors of a tridiagonal matrix. DLAED7 handles the case in which eigenvalues only or eigenvalues and eigenvectors of a full symmetric matrix (which was reduced to tridiagonal form) are desired. T = Q(in) ( D(in) + RHO * Z*Z**T ) Q**T(in) = Q(out) * D(out) * Q**T(out) where Z = Q**T*u, u is a vector of length N with ones in the CUTPNT and CUTPNT + 1 th elements and zeros elsewhere. The eigenvectors of the original matrix are stored in Q, and the eigenvalues are in D. The algorithm consists of three stages: The first stage consists of deflating the size of the problem when there are multiple eigenvalues or if there is a zero in the Z vector. For each such occurrence the dimension of the secular equation problem is reduced by one. This stage is performed by the routine DLAED2. The second stage consists of calculating the updated eigenvalues. This is done by finding the roots of the secular equation via the routine DLAED4 (as called by DLAED3). This routine also calculates the eigenvectors of the current problem. The final stage consists of computing the updated eigenvectors directly using the updated eigenvalues. The eigenvectors for the current problem are multiplied with the eigenvectors from the overall problem.

Here is the call graph for this function:

la_dlaed2()

pure subroutine, public la_lapack_d::la_dlaed2	(	integer(ilp), intent(out)	k,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	n1,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(ldq,*), intent(inout)	q,
		integer(ilp), intent(in)	ldq,
		integer(ilp), dimension(*), intent(inout)	indxq,
		real(dp), intent(inout)	rho,
		real(dp), dimension(*), intent(inout)	z,
		real(dp), dimension(*), intent(out)	dlamda,
		real(dp), dimension(*), intent(out)	w,
		real(dp), dimension(*), intent(out)	q2,
		integer(ilp), dimension(*), intent(out)	indx,
		integer(ilp), dimension(*), intent(out)	indxc,
		integer(ilp), dimension(*), intent(out)	indxp,
		integer(ilp), dimension(*), intent(out)	coltyp,
		integer(ilp), intent(out)	info
	)

DLAED2: merges the two sets of eigenvalues together into a single sorted set. Then it tries to deflate the size of the problem. There are two ways in which deflation can occur: when two or more eigenvalues are close together or if there is a tiny entry in the Z vector. For each such occurrence the order of the related secular equation problem is reduced by one.

Here is the call graph for this function:

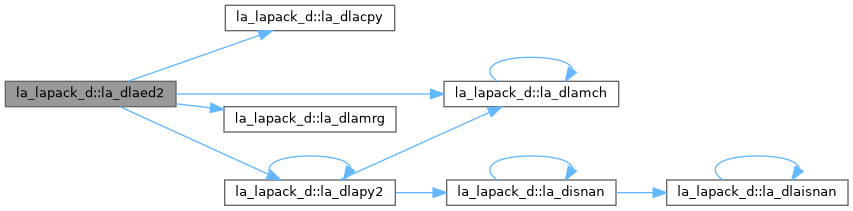
la_dlaed3()

pure subroutine, public la_lapack_d::la_dlaed3	(	integer(ilp), intent(in)	k,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	n1,
		real(dp), dimension(*), intent(out)	d,
		real(dp), dimension(ldq,*), intent(out)	q,
		integer(ilp), intent(in)	ldq,
		real(dp), intent(in)	rho,
		real(dp), dimension(*), intent(inout)	dlamda,
		real(dp), dimension(*), intent(in)	q2,
		integer(ilp), dimension(*), intent(in)	indx,
		integer(ilp), dimension(*), intent(in)	ctot,
		real(dp), dimension(*), intent(inout)	w,
		real(dp), dimension(*), intent(out)	s,
		integer(ilp), intent(out)	info
	)

DLAED3: finds the roots of the secular equation, as defined by the values in D, W, and RHO, between 1 and K. It makes the appropriate calls to DLAED4 and then updates the eigenvectors by multiplying the matrix of eigenvectors of the pair of eigensystems being combined by the matrix of eigenvectors of the K-by-K system which is solved here. This code makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none.

Here is the call graph for this function:

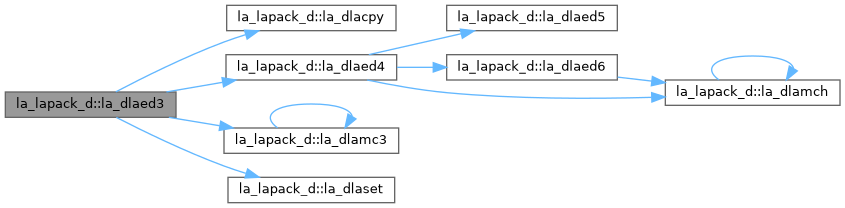
la_dlaed4()

pure subroutine, public la_lapack_d::la_dlaed4	(	integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	i,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(in)	z,
		real(dp), dimension(*), intent(out)	delta,
		real(dp), intent(in)	rho,
		real(dp), intent(out)	dlam,
		integer(ilp), intent(out)	info
	)

This subroutine computes the I-th updated eigenvalue of a symmetric rank-one modification to a diagonal matrix whose elements are given in the array d, and that D(i) < D(j) for i < j and that RHO > 0. This is arranged by the calling routine, and is no loss in generality. The rank-one modified system is thus diag( D ) + RHO * Z * Z_transpose. where we assume the Euclidean norm of Z is 1. The method consists of approximating the rational functions in the secular equation by simpler interpolating rational functions.

Here is the call graph for this function:

la_dlaed5()

pure subroutine, public la_lapack_d::la_dlaed5	(	integer(ilp), intent(in)	i,
		real(dp), dimension(2), intent(in)	d,
		real(dp), dimension(2), intent(in)	z,
		real(dp), dimension(2), intent(out)	delta,
		real(dp), intent(in)	rho,
		real(dp), intent(out)	dlam
	)

This subroutine computes the I-th eigenvalue of a symmetric rank-one modification of a 2-by-2 diagonal matrix diag( D ) + RHO * Z * transpose(Z) . The diagonal elements in the array D are assumed to satisfy D(i) < D(j) for i < j . We also assume RHO > 0 and that the Euclidean norm of the vector Z is one.

la_dlaed6()

pure subroutine, public la_lapack_d::la_dlaed6	(	integer(ilp), intent(in)	kniter,
		logical(lk), intent(in)	orgati,
		real(dp), intent(in)	rho,
		real(dp), dimension(3), intent(in)	d,
		real(dp), dimension(3), intent(in)	z,
		real(dp), intent(in)	finit,
		real(dp), intent(out)	tau,
		integer(ilp), intent(out)	info
	)

DLAED6: computes the positive or negative root (closest to the origin) of z(1) z(2) z(3) f(x) = rho + ------— + -------— + ------— d(1)-x d(2)-x d(3)-x It is assumed that if ORGATI = .true. the root is between d(2) and d(3); otherwise it is between d(1) and d(2) This routine will be called by DLAED4 when necessary. In most cases, the root sought is the smallest in magnitude, though it might not be in some extremely rare situations.

Here is the call graph for this function:

la_dlaed7()

pure subroutine, public la_lapack_d::la_dlaed7	(	integer(ilp), intent(in)	icompq,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	qsiz,
		integer(ilp), intent(in)	tlvls,
		integer(ilp), intent(in)	curlvl,
		integer(ilp), intent(in)	curpbm,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(ldq,*), intent(inout)	q,
		integer(ilp), intent(in)	ldq,
		integer(ilp), dimension(*), intent(out)	indxq,
		real(dp), intent(inout)	rho,
		integer(ilp), intent(in)	cutpnt,
		real(dp), dimension(*), intent(inout)	qstore,
		integer(ilp), dimension(*), intent(inout)	qptr,
		integer(ilp), dimension(*), intent(inout)	prmptr,
		integer(ilp), dimension(*), intent(inout)	perm,
		integer(ilp), dimension(*), intent(inout)	givptr,
		integer(ilp), dimension(2,*), intent(inout)	givcol,
		real(dp), dimension(2,*), intent(inout)	givnum,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DLAED7: computes the updated eigensystem of a diagonal matrix after modification by a rank-one symmetric matrix. This routine is used only for the eigenproblem which requires all eigenvalues and optionally eigenvectors of a dense symmetric matrix that has been reduced to tridiagonal form. DLAED1 handles the case in which all eigenvalues and eigenvectors of a symmetric tridiagonal matrix are desired. T = Q(in) ( D(in) + RHO * Z*Z**T ) Q**T(in) = Q(out) * D(out) * Q**T(out) where Z = Q**Tu, u is a vector of length N with ones in the CUTPNT and CUTPNT + 1 th elements and zeros elsewhere. The eigenvectors of the original matrix are stored in Q, and the eigenvalues are in D. The algorithm consists of three stages: The first stage consists of deflating the size of the problem when there are multiple eigenvalues or if there is a zero in the Z vector. For each such occurrence the dimension of the secular equation problem is reduced by one. This stage is performed by the routine DLAED8. The second stage consists of calculating the updated eigenvalues. This is done by finding the roots of the secular equation via the routine DLAED4 (as called by DLAED9). This routine also calculates the eigenvectors of the current problem. The final stage consists of computing the updated eigenvectors directly using the updated eigenvalues. The eigenvectors for the current problem are multiplied with the eigenvectors from the overall problem.

Here is the call graph for this function:

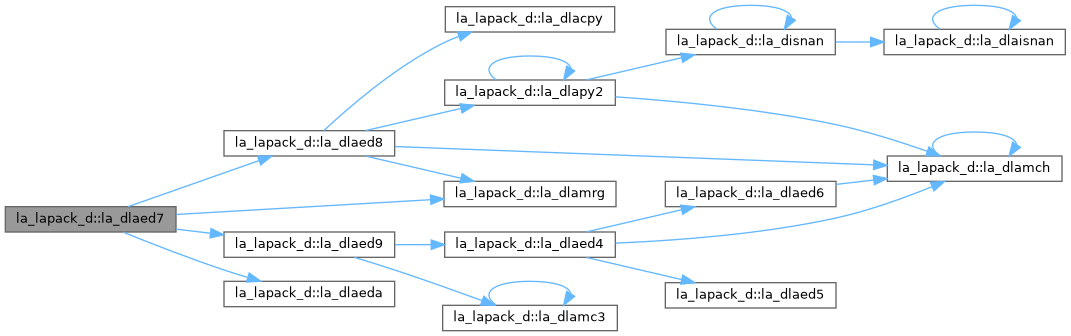
la_dlaed8()

pure subroutine, public la_lapack_d::la_dlaed8	(	integer(ilp), intent(in)	icompq,
		integer(ilp), intent(out)	k,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	qsiz,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(ldq,*), intent(inout)	q,
		integer(ilp), intent(in)	ldq,
		integer(ilp), dimension(*), intent(inout)	indxq,
		real(dp), intent(inout)	rho,
		integer(ilp), intent(in)	cutpnt,
		real(dp), dimension(*), intent(inout)	z,
		real(dp), dimension(*), intent(out)	dlamda,
		real(dp), dimension(ldq2,*), intent(out)	q2,
		integer(ilp), intent(in)	ldq2,
		real(dp), dimension(*), intent(out)	w,
		integer(ilp), dimension(*), intent(out)	perm,
		integer(ilp), intent(out)	givptr,
		integer(ilp), dimension(2,*), intent(out)	givcol,
		real(dp), dimension(2,*), intent(out)	givnum,
		integer(ilp), dimension(*), intent(out)	indxp,
		integer(ilp), dimension(*), intent(out)	indx,
		integer(ilp), intent(out)	info
	)

DLAED8: merges the two sets of eigenvalues together into a single sorted set. Then it tries to deflate the size of the problem. There are two ways in which deflation can occur: when two or more eigenvalues are close together or if there is a tiny element in the Z vector. For each such occurrence the order of the related secular equation problem is reduced by one.

Here is the call graph for this function:

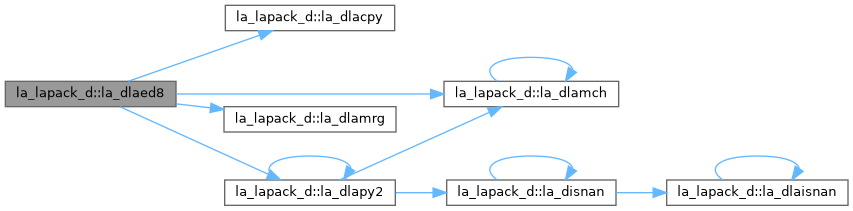
la_dlaed9()

pure subroutine, public la_lapack_d::la_dlaed9	(	integer(ilp), intent(in)	k,
		integer(ilp), intent(in)	kstart,
		integer(ilp), intent(in)	kstop,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(out)	d,
		real(dp), dimension(ldq,*), intent(out)	q,
		integer(ilp), intent(in)	ldq,
		real(dp), intent(in)	rho,
		real(dp), dimension(*), intent(inout)	dlamda,
		real(dp), dimension(*), intent(inout)	w,
		real(dp), dimension(lds,*), intent(out)	s,
		integer(ilp), intent(in)	lds,
		integer(ilp), intent(out)	info
	)

DLAED9: finds the roots of the secular equation, as defined by the values in D, Z, and RHO, between KSTART and KSTOP. It makes the appropriate calls to DLAED4 and then stores the new matrix of eigenvectors for use in calculating the next level of Z vectors.

Here is the call graph for this function:

la_dlaeda()

pure subroutine, public la_lapack_d::la_dlaeda	(	integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	tlvls,
		integer(ilp), intent(in)	curlvl,
		integer(ilp), intent(in)	curpbm,
		integer(ilp), dimension(*), intent(in)	prmptr,
		integer(ilp), dimension(*), intent(in)	perm,
		integer(ilp), dimension(*), intent(in)	givptr,
		integer(ilp), dimension(2,*), intent(in)	givcol,
		real(dp), dimension(2,*), intent(in)	givnum,
		real(dp), dimension(*), intent(in)	q,
		integer(ilp), dimension(*), intent(in)	qptr,
		real(dp), dimension(*), intent(out)	z,
		real(dp), dimension(*), intent(out)	ztemp,
		integer(ilp), intent(out)	info
	)

DLAEDA: computes the Z vector corresponding to the merge step in the CURLVLth step of the merge process with TLVLS steps for the CURPBMth problem.

la_dlaein()

pure subroutine, public la_lapack_d::la_dlaein	(	logical(lk), intent(in)	rightv,
		logical(lk), intent(in)	noinit,
		integer(ilp), intent(in)	n,
		real(dp), dimension(ldh,*), intent(in)	h,
		integer(ilp), intent(in)	ldh,
		real(dp), intent(in)	wr,
		real(dp), intent(in)	wi,
		real(dp), dimension(*), intent(inout)	vr,
		real(dp), dimension(*), intent(inout)	vi,
		real(dp), dimension(ldb,*), intent(out)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(*), intent(out)	work,
		real(dp), intent(in)	eps3,
		real(dp), intent(in)	smlnum,
		real(dp), intent(in)	bignum,
		integer(ilp), intent(out)	info
	)

DLAEIN: uses inverse iteration to find a right or left eigenvector corresponding to the eigenvalue (WR,WI) of a real upper Hessenberg matrix H.

Here is the call graph for this function:

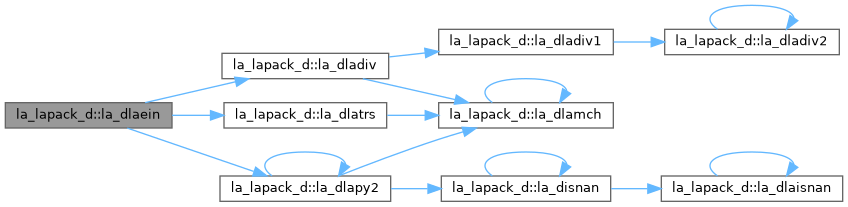
la_dlaev2()

pure subroutine, public la_lapack_d::la_dlaev2	(	real(dp), intent(in)	a,
		real(dp), intent(in)	b,
		real(dp), intent(in)	c,
		real(dp), intent(out)	rt1,
		real(dp), intent(out)	rt2,
		real(dp), intent(out)	cs1,
		real(dp), intent(out)	sn1
	)

DLAEV2: computes the eigendecomposition of a 2-by-2 symmetric matrix [ A B ] [ B C ]. On return, RT1 is the eigenvalue of larger absolute value, RT2 is the eigenvalue of smaller absolute value, and (CS1,SN1) is the unit right eigenvector for RT1, giving the decomposition [ CS1 SN1 ] [ A B ] [ CS1 -SN1 ] = [ RT1 0 ] [-SN1 CS1 ] [ B C ] [ SN1 CS1 ] [ 0 RT2 ].

la_dlaexc()

subroutine, public la_lapack_d::la_dlaexc	(	logical(lk), intent(in)	wantq,
		integer(ilp), intent(in)	n,
		real(dp), dimension(ldt,*), intent(inout)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(ldq,*), intent(inout)	q,
		integer(ilp), intent(in)	ldq,
		integer(ilp), intent(in)	j1,
		integer(ilp), intent(in)	n1,
		integer(ilp), intent(in)	n2,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DLAEXC: swaps adjacent diagonal blocks T11 and T22 of order 1 or 2 in an upper quasi-triangular matrix T by an orthogonal similarity transformation. T must be in Schur canonical form, that is, block upper triangular with 1-by-1 and 2-by-2 diagonal blocks; each 2-by-2 diagonal block has its diagonal elements equal and its off-diagonal elements of opposite sign.

Here is the call graph for this function:

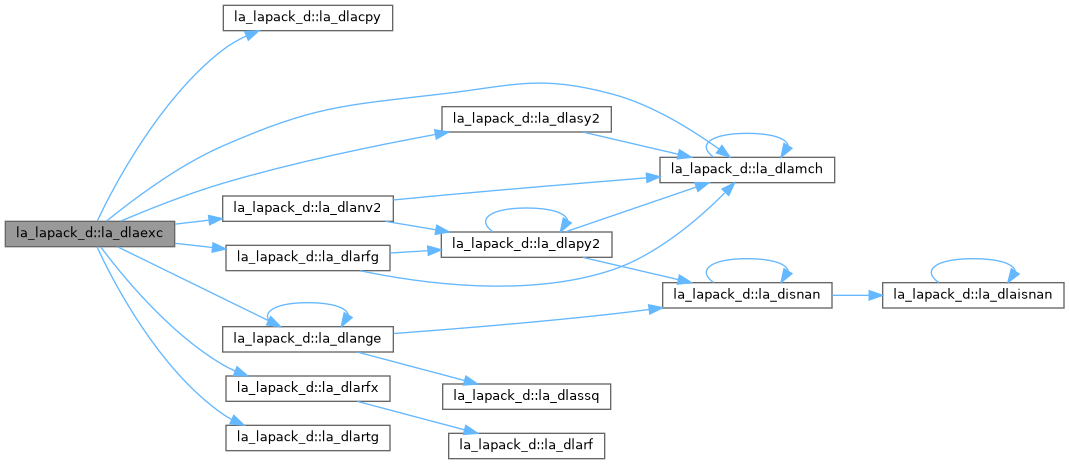
la_dlag2()

pure subroutine, public la_lapack_d::la_dlag2	(	real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), intent(in)	safmin,
		real(dp), intent(out)	scale1,
		real(dp), intent(out)	scale2,
		real(dp), intent(out)	wr1,
		real(dp), intent(out)	wr2,
		real(dp), intent(out)	wi
	)

DLAG2: computes the eigenvalues of a 2 x 2 generalized eigenvalue problem A - w B, with scaling as necessary to avoid over-/underflow. The scaling factor "s" results in a modified eigenvalue equation s A - w B where s is a non-negative scaling factor chosen so that w, w B, and s A do not overflow and, if possible, do not underflow, either.

la_dlag2q()

pure subroutine, public la_lapack_d::la_dlag2q	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(ldsa,*), intent(in)	sa,
		integer(ilp), intent(in)	ldsa,
		real(qp), dimension(lda,*), intent(out)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), intent(out)	info
	)

DLAG2Q: converts a SINGLE PRECISION matrix, SA, to a DOUBLE PRECISION matrix, A. Note that while it is possible to overflow while converting from double to single, it is not possible to overflow when converting from single to double. This is an auxiliary routine so there is no argument checking.

la_dlag2s()

pure subroutine, public la_lapack_d::la_dlag2s	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(sp), dimension(ldsa,*), intent(out)	sa,
		integer(ilp), intent(in)	ldsa,
		integer(ilp), intent(out)	info
	)

DLAG2S: converts a DOUBLE PRECISION matrix, SA, to a SINGLE PRECISION matrix, A. RMAX is the overflow for the SINGLE PRECISION arithmetic DLAG2S checks that all the entries of A are between -RMAX and RMAX. If not the conversion is aborted and a flag is raised. This is an auxiliary routine so there is no argument checking.

Here is the call graph for this function:

la_dlags2()

pure subroutine, public la_lapack_d::la_dlags2	(	logical(lk), intent(in)	upper,
		real(dp), intent(in)	a1,
		real(dp), intent(in)	a2,
		real(dp), intent(in)	a3,
		real(dp), intent(in)	b1,
		real(dp), intent(in)	b2,
		real(dp), intent(in)	b3,
		real(dp), intent(out)	csu,
		real(dp), intent(out)	snu,
		real(dp), intent(out)	csv,
		real(dp), intent(out)	snv,
		real(dp), intent(out)	csq,
		real(dp), intent(out)	snq
	)

DLAGS2: computes 2-by-2 orthogonal matrices U, V and Q, such that if ( UPPER ) then U**T A*Q = U**T *( A1 A2 )*Q = ( x 0 ) ( 0 A3 ) ( x x ) and V**T*B*Q = V**T *( B1 B2 )*Q = ( x 0 ) ( 0 B3 ) ( x x ) or if ( .NOT.UPPER ) then U**T *A*Q = U**T *( A1 0 )*Q = ( x x ) ( A2 A3 ) ( 0 x ) and V**T*B*Q = V**T( B1 0 )*Q = ( x x ) ( B2 B3 ) ( 0 x ) The rows of the transformed A and B are parallel, where U = ( CSU SNU ), V = ( CSV SNV ), Q = ( CSQ SNQ ) ( -SNU CSU ) ( -SNV CSV ) ( -SNQ CSQ ) Z**T denotes the transpose of Z.

Here is the call graph for this function:

la_dlagtf()

pure subroutine, public la_lapack_d::la_dlagtf	(	integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	a,
		real(dp), intent(in)	lambda,
		real(dp), dimension(*), intent(inout)	b,
		real(dp), dimension(*), intent(inout)	c,
		real(dp), intent(in)	tol,
		real(dp), dimension(*), intent(out)	d,
		integer(ilp), dimension(*), intent(out)	in,
		integer(ilp), intent(out)	info
	)

DLAGTF: factorizes the matrix (T - lambda*I), where T is an n by n tridiagonal matrix and lambda is a scalar, as T - lambda*I = PLU, where P is a permutation matrix, L is a unit lower tridiagonal matrix with at most one non-zero sub-diagonal elements per column and U is an upper triangular matrix with at most two non-zero super-diagonal elements per column. The factorization is obtained by Gaussian elimination with partial pivoting and implicit row scaling. The parameter LAMBDA is included in the routine so that DLAGTF may be used, in conjunction with DLAGTS, to obtain eigenvectors of T by inverse iteration.

Here is the call graph for this function:

la_dlagtm()

pure subroutine, public la_lapack_d::la_dlagtm	(	character, intent(in)	trans,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), intent(in)	alpha,
		real(dp), dimension(*), intent(in)	dl,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(in)	du,
		real(dp), dimension(ldx,*), intent(in)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), intent(in)	beta,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb
	)

DLAGTM: performs a matrix-vector product of the form B := alpha * A * X + beta * B where A is a tridiagonal matrix of order N, B and X are N by NRHS matrices, and alpha and beta are real scalars, each of which may be 0., 1., or -1.

la_dlagts()

pure subroutine, public la_lapack_d::la_dlagts	(	integer(ilp), intent(in)	job,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(in)	a,
		real(dp), dimension(*), intent(in)	b,
		real(dp), dimension(*), intent(in)	c,
		real(dp), dimension(*), intent(in)	d,
		integer(ilp), dimension(*), intent(in)	in,
		real(dp), dimension(*), intent(inout)	y,
		real(dp), intent(inout)	tol,
		integer(ilp), intent(out)	info
	)

DLAGTS: may be used to solve one of the systems of equations (T - lambda*I)*x = y or (T - lambda*I)**T*x = y, where T is an n by n tridiagonal matrix, for x, following the factorization of (T - lambda*I) as (T - lambda*I) = P*L*U , by routine DLAGTF. The choice of equation to be solved is controlled by the argument JOB, and in each case there is an option to perturb zero or very small diagonal elements of U, this option being intended for use in applications such as inverse iteration.

Here is the call graph for this function:

la_dlagv2()

pure subroutine, public la_lapack_d::la_dlagv2	(	real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(2), intent(out)	alphar,
		real(dp), dimension(2), intent(out)	alphai,
		real(dp), dimension(2), intent(out)	beta,
		real(dp), intent(out)	csl,
		real(dp), intent(out)	snl,
		real(dp), intent(out)	csr,
		real(dp), intent(out)	snr
	)

DLAGV2: computes the Generalized Schur factorization of a real 2-by-2 matrix pencil (A,B) where B is upper triangular. This routine computes orthogonal (rotation) matrices given by CSL, SNL and CSR, SNR such that 1) if the pencil (A,B) has two real eigenvalues (include 0/0 or 1/0 types), then [ a11 a12 ] := [ CSL SNL ] [ a11 a12 ] [ CSR -SNR ] [ 0 a22 ] [ -SNL CSL ] [ a21 a22 ] [ SNR CSR ] [ b11 b12 ] := [ CSL SNL ] [ b11 b12 ] [ CSR -SNR ] [ 0 b22 ] [ -SNL CSL ] [ 0 b22 ] [ SNR CSR ], 2) if the pencil (A,B) has a pair of complex conjugate eigenvalues, then [ a11 a12 ] := [ CSL SNL ] [ a11 a12 ] [ CSR -SNR ] [ a21 a22 ] [ -SNL CSL ] [ a21 a22 ] [ SNR CSR ] [ b11 0 ] := [ CSL SNL ] [ b11 b12 ] [ CSR -SNR ] [ 0 b22 ] [ -SNL CSL ] [ 0 b22 ] [ SNR CSR ] where b11 >= b22 > 0.

Here is the call graph for this function:

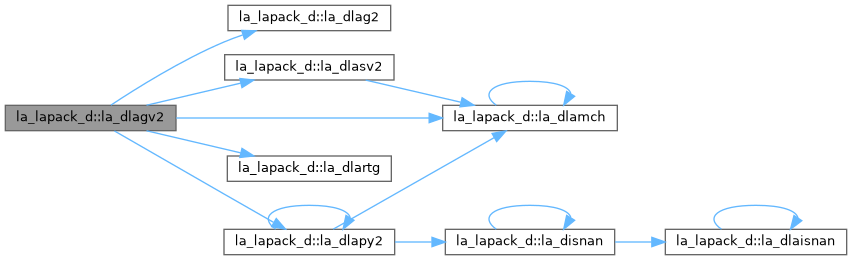
la_dlahqr()

pure subroutine, public la_lapack_d::la_dlahqr	(	logical(lk), intent(in)	wantt,
		logical(lk), intent(in)	wantz,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ilo,
		integer(ilp), intent(in)	ihi,
		real(dp), dimension(ldh,*), intent(inout)	h,
		integer(ilp), intent(in)	ldh,
		real(dp), dimension(*), intent(out)	wr,
		real(dp), dimension(*), intent(out)	wi,
		integer(ilp), intent(in)	iloz,
		integer(ilp), intent(in)	ihiz,
		real(dp), dimension(ldz,*), intent(inout)	z,
		integer(ilp), intent(in)	ldz,
		integer(ilp), intent(out)	info
	)

DLAHQR: is an auxiliary routine called by DHSEQR to update the eigenvalues and Schur decomposition already computed by DHSEQR, by dealing with the Hessenberg submatrix in rows and columns ILO to IHI.

Here is the call graph for this function:

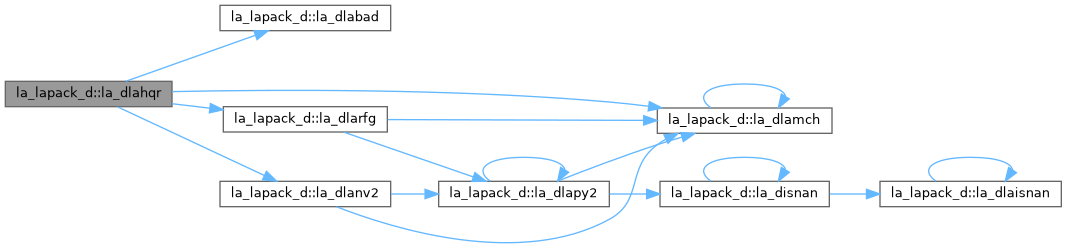
la_dlahr2()

pure subroutine, public la_lapack_d::la_dlahr2	(	integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		integer(ilp), intent(in)	nb,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(nb), intent(out)	tau,
		real(dp), dimension(ldt,nb), intent(out)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(ldy,nb), intent(out)	y,
		integer(ilp), intent(in)	ldy
	)

DLAHR2: reduces the first NB columns of A real general n-BY-(n-k+1) matrix A so that elements below the k-th subdiagonal are zero. The reduction is performed by an orthogonal similarity transformation Q**T * A * Q. The routine returns the matrices V and T which determine Q as a block reflector I - V*T*V**T, and also the matrix Y = A * V * T. This is an auxiliary routine called by DGEHRD.

Here is the call graph for this function:

la_dlaic1()

pure subroutine, public la_lapack_d::la_dlaic1	(	integer(ilp), intent(in)	job,
		integer(ilp), intent(in)	j,
		real(dp), dimension(j), intent(in)	x,
		real(dp), intent(in)	sest,
		real(dp), dimension(j), intent(in)	w,
		real(dp), intent(in)	gamma,
		real(dp), intent(out)	sestpr,
		real(dp), intent(out)	s,
		real(dp), intent(out)	c
	)

DLAIC1: applies one step of incremental condition estimation in its simplest version: Let x, twonorm(x) = 1, be an approximate singular vector of an j-by-j lower triangular matrix L, such that twonorm(L*x) = sest Then DLAIC1 computes sestpr, s, c such that the vector [ s*x ] xhat = [ c ] is an approximate singular vector of [ L 0 ] Lhat = [ w**T gamma ] in the sense that twonorm(Lhat*xhat) = sestpr. Depending on JOB, an estimate for the largest or smallest singular value is computed. Note that [s c]**T and sestpr**2 is an eigenpair of the system diag(sest*sest, 0) + [alpha gamma] * [ alpha ] [ gamma ] where alpha = x**T*w.

Here is the call graph for this function:

la_dlaisnan()

pure logical(lk) function, public la_lapack_d::la_dlaisnan	(	real(dp), intent(in)	din1,
		real(dp), intent(in)	din2
	)

This routine is not for general use. It exists solely to avoid over-optimization in DISNAN. DLAISNAN: checks for NaNs by comparing its two arguments for inequality. NaN is the only floating-point value where NaN != NaN returns .TRUE. To check for NaNs, pass the same variable as both arguments. A compiler must assume that the two arguments are not the same variable, and the test will not be optimized away. Interprocedural or whole-program optimization may delete this test. The ISNAN functions will be replaced by the correct Fortran 03 intrinsic once the intrinsic is widely available.

Here is the call graph for this function:

la_dlaln2()

pure subroutine, public la_lapack_d::la_dlaln2	(	logical(lk), intent(in)	ltrans,
		integer(ilp), intent(in)	na,
		integer(ilp), intent(in)	nw,
		real(dp), intent(in)	smin,
		real(dp), intent(in)	ca,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), intent(in)	d1,
		real(dp), intent(in)	d2,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), intent(in)	wr,
		real(dp), intent(in)	wi,
		real(dp), dimension(ldx,*), intent(out)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), intent(out)	scale,
		real(dp), intent(out)	xnorm,
		integer(ilp), intent(out)	info
	)

DLALN2: solves a system of the form (ca A - w D ) X = s B or (ca A**T - w D) X = s B with possible scaling ("s") and perturbation of A. (A**T means A-transpose.) A is an NA x NA real matrix, ca is a real scalar, D is an NA x NA real diagonal matrix, w is a real or complex value, and X and B are NA x 1 matrices – real if w is real, complex if w is complex. NA may be 1 or 2. If w is complex, X and B are represented as NA x 2 matrices, the first column of each being the real part and the second being the imaginary part. "s" is a scaling factor (<= 1), computed by DLALN2, which is so chosen that X can be computed without overflow. X is further scaled if necessary to assure that norm(ca A - w D)*norm(X) is less than overflow. If both singular values of (ca A - w D) are less than SMIN, SMIN*identity will be used instead of (ca A - w D). If only one singular value is less than SMIN, one element of (ca A - w D) will be perturbed enough to make the smallest singular value roughly SMIN. If both singular values are at least SMIN, (ca A - w D) will not be perturbed. In any case, the perturbation will be at most some small multiple of max( SMIN, ulp*norm(ca A - w D) ). The singular values are computed by infinity-norm approximations, and thus will only be correct to a factor of 2 or so. Note: all input quantities are assumed to be smaller than overflow by a reasonable factor. (See BIGNUM.)

Here is the call graph for this function:

la_dlals0()

pure subroutine, public la_lapack_d::la_dlals0	(	integer(ilp), intent(in)	icompq,
		integer(ilp), intent(in)	nl,
		integer(ilp), intent(in)	nr,
		integer(ilp), intent(in)	sqre,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldbx,*), intent(out)	bx,
		integer(ilp), intent(in)	ldbx,
		integer(ilp), dimension(*), intent(in)	perm,
		integer(ilp), intent(in)	givptr,
		integer(ilp), dimension(ldgcol,*), intent(in)	givcol,
		integer(ilp), intent(in)	ldgcol,
		real(dp), dimension(ldgnum,*), intent(in)	givnum,
		integer(ilp), intent(in)	ldgnum,
		real(dp), dimension(ldgnum,*), intent(in)	poles,
		real(dp), dimension(*), intent(in)	difl,
		real(dp), dimension(ldgnum,*), intent(in)	difr,
		real(dp), dimension( *), intent(in)	z,
		integer(ilp), intent(in)	k,
		real(dp), intent(in)	c,
		real(dp), intent(in)	s,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DLALS0: applies back the multiplying factors of either the left or the right singular vector matrix of a diagonal matrix appended by a row to the right hand side matrix B in solving the least squares problem using the divide-and-conquer SVD approach. For the left singular vector matrix, three types of orthogonal matrices are involved: (1L) Givens rotations: the number of such rotations is GIVPTR; the pairs of columns/rows they were applied to are stored in GIVCOL; and the C- and S-values of these rotations are stored in GIVNUM. (2L) Permutation. The (NL+1)-st row of B is to be moved to the first row, and for J=2:N, PERM(J)-th row of B is to be moved to the J-th row. (3L) The left singular vector matrix of the remaining matrix. For the right singular vector matrix, four types of orthogonal matrices are involved: (1R) The right singular vector matrix of the remaining matrix. (2R) If SQRE = 1, one extra Givens rotation to generate the right null space. (3R) The inverse transformation of (2L). (4R) The inverse transformation of (1L).

Here is the call graph for this function:

la_dlalsa()

pure subroutine, public la_lapack_d::la_dlalsa	(	integer(ilp), intent(in)	icompq,
		integer(ilp), intent(in)	smlsiz,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldbx,*), intent(out)	bx,
		integer(ilp), intent(in)	ldbx,
		real(dp), dimension(ldu,*), intent(in)	u,
		integer(ilp), intent(in)	ldu,
		real(dp), dimension(ldu,*), intent(in)	vt,
		integer(ilp), dimension(*), intent(in)	k,
		real(dp), dimension(ldu,*), intent(in)	difl,
		real(dp), dimension(ldu,*), intent(in)	difr,
		real(dp), dimension(ldu,*), intent(in)	z,
		real(dp), dimension(ldu,*), intent(in)	poles,
		integer(ilp), dimension(*), intent(in)	givptr,
		integer(ilp), dimension(ldgcol,*), intent(in)	givcol,
		integer(ilp), intent(in)	ldgcol,
		integer(ilp), dimension(ldgcol,*), intent(in)	perm,
		real(dp), dimension(ldu,*), intent(in)	givnum,
		real(dp), dimension(*), intent(in)	c,
		real(dp), dimension( *), intent(in)	s,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DLALSA: is an itermediate step in solving the least squares problem by computing the SVD of the coefficient matrix in compact form (The singular vectors are computed as products of simple orthorgonal matrices.). If ICOMPQ = 0, DLALSA applies the inverse of the left singular vector matrix of an upper bidiagonal matrix to the right hand side; and if ICOMPQ = 1, DLALSA applies the right singular vector matrix to the right hand side. The singular vector matrices were generated in compact form by DLALSA.

Here is the call graph for this function:

la_dlalsd()

pure subroutine, public la_lapack_d::la_dlalsd	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	smlsiz,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(inout)	e,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), intent(in)	rcond,
		integer(ilp), intent(out)	rank,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DLALSD: uses the singular value decomposition of A to solve the least squares problem of finding X to minimize the Euclidean norm of each column of A*X-B, where A is N-by-N upper bidiagonal, and X and B are N-by-NRHS. The solution X overwrites B. The singular values of A smaller than RCOND times the largest singular value are treated as zero in solving the least squares problem; in this case a minimum norm solution is returned. The actual singular values are returned in D in ascending order. This code makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray XMP, Cray YMP, Cray C 90, or Cray 2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none.

Here is the call graph for this function:

la_dlamc3()

pure real(dp) function, public la_lapack_d::la_dlamc3	(	real(dp), intent(in)	a,
		real(dp), intent(in)	b
	)

Here is the call graph for this function:

la_dlamch()

pure real(dp) function, public la_lapack_d::la_dlamch

(

character, intent(in)

cmach

)

DLAMCH: determines double precision machine parameters.

Here is the call graph for this function:

la_dlamrg()

pure subroutine, public la_lapack_d::la_dlamrg	(	integer(ilp), intent(in)	n1,
		integer(ilp), intent(in)	n2,
		real(dp), dimension(*), intent(in)	a,
		integer(ilp), intent(in)	dtrd1,
		integer(ilp), intent(in)	dtrd2,
		integer(ilp), dimension(*), intent(out)	index
	)

DLAMRG: will create a permutation list which will merge the elements of A (which is composed of two independently sorted sets) into a single set which is sorted in ascending order.

la_dlamswlq()

pure subroutine, public la_lapack_d::la_dlamswlq	(	character, intent(in)	side,
		character, intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		integer(ilp), intent(in)	mb,
		integer(ilp), intent(in)	nb,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldt,*), intent(in)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DLAMSWLQ: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q * C C * Q TRANS = 'T': Q**T * C C * Q**T where Q is a real orthogonal matrix defined as the product of blocked elementary reflectors computed by short wide LQ factorization (DLASWLQ)

Here is the call graph for this function:

la_dlamtsqr()

pure subroutine, public la_lapack_d::la_dlamtsqr	(	character, intent(in)	side,
		character, intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		integer(ilp), intent(in)	mb,
		integer(ilp), intent(in)	nb,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldt,*), intent(in)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DLAMTSQR: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q * C C * Q TRANS = 'T': Q**T * C C * Q**T where Q is a real orthogonal matrix defined as the product of blocked elementary reflectors computed by tall skinny QR factorization (DLATSQR)

Here is the call graph for this function:

la_dlaneg()

pure integer(ilp) function, public la_lapack_d::la_dlaneg	(	integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(in)	lld,
		real(dp), intent(in)	sigma,
		real(dp), intent(in)	pivmin,
		integer(ilp), intent(in)	r
	)

DLANEG: computes the Sturm count, the number of negative pivots encountered while factoring tridiagonal T - sigma I = L D L^T. This implementation works directly on the factors without forming the tridiagonal matrix T. The Sturm count is also the number of eigenvalues of T less than sigma. This routine is called from DLARRB. The current routine does not use the PIVMIN parameter but rather requires IEEE-754 propagation of Infinities and NaNs. This routine also has no input range restrictions but does require default exception handling such that x/0 produces Inf when x is non-zero, and Inf/Inf produces NaN. For more information, see: Marques, Riedy, and Voemel, "Benefits of IEEE-754 Features in Modern Symmetric Tridiagonal Eigensolvers," SIAM Journal on Scientific Computing, v28, n5, 2006. DOI 10.1137/050641624 (Tech report version in LAWN 172 with the same title.)

Here is the call graph for this function:

la_dlangb()

real(dp) function, public la_lapack_d::la_dlangb	(	character, intent(in)	norm,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kl,
		integer(ilp), intent(in)	ku,
		real(dp), dimension(ldab,*), intent(in)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(*), intent(out)	work
	)

DLANGB: returns the value of the one norm, or the Frobenius norm, or the infinity norm, or the element of largest absolute value of an n by n band matrix A, with kl sub-diagonals and ku super-diagonals.

Here is the call graph for this function:

la_dlange()

real(dp) function, public la_lapack_d::la_dlange	(	character, intent(in)	norm,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	work
	)

DLANGE: returns the value of the one norm, or the Frobenius norm, or the infinity norm, or the element of largest absolute value of a real matrix A.

Here is the call graph for this function:

la_dlangt()

pure real(dp) function, public la_lapack_d::la_dlangt	(	character, intent(in)	norm,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(in)	dl,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(in)	du
	)

DLANGT: returns the value of the one norm, or the Frobenius norm, or the infinity norm, or the element of largest absolute value of a real tridiagonal matrix A.

Here is the call graph for this function:

la_dlanhs()

real(dp) function, public la_lapack_d::la_dlanhs	(	character, intent(in)	norm,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	work
	)

DLANHS: returns the value of the one norm, or the Frobenius norm, or the infinity norm, or the element of largest absolute value of a Hessenberg matrix A.

Here is the call graph for this function:

la_dlansb()

real(dp) function, public la_lapack_d::la_dlansb	(	character, intent(in)	norm,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		real(dp), dimension(ldab,*), intent(in)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(*), intent(out)	work
	)

DLANSB: returns the value of the one norm, or the Frobenius norm, or the infinity norm, or the element of largest absolute value of an n by n symmetric band matrix A, with k super-diagonals.

Here is the call graph for this function:

la_dlansf()

real(dp) function, public la_lapack_d::la_dlansf	(	character, intent(in)	norm,
		character, intent(in)	transr,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(0:*), intent(in)	a,
		real(dp), dimension(0:*), intent(out)	work
	)

DLANSF: returns the value of the one norm, or the Frobenius norm, or the infinity norm, or the element of largest absolute value of a real symmetric matrix A in RFP format.

Here is the call graph for this function:

la_dlansp()

real(dp) function, public la_lapack_d::la_dlansp	(	character, intent(in)	norm,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(in)	ap,
		real(dp), dimension(*), intent(out)	work
	)

DLANSP: returns the value of the one norm, or the Frobenius norm, or the infinity norm, or the element of largest absolute value of a real symmetric matrix A, supplied in packed form.

Here is the call graph for this function:

la_dlanst()

pure real(dp) function, public la_lapack_d::la_dlanst	(	character, intent(in)	norm,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(in)	e
	)

DLANST: returns the value of the one norm, or the Frobenius norm, or the infinity norm, or the element of largest absolute value of a real symmetric tridiagonal matrix A.

Here is the call graph for this function:

la_dlansy()

real(dp) function, public la_lapack_d::la_dlansy	(	character, intent(in)	norm,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	work
	)

DLANSY: returns the value of the one norm, or the Frobenius norm, or the infinity norm, or the element of largest absolute value of a real symmetric matrix A.

Here is the call graph for this function:

la_dlantb()

real(dp) function, public la_lapack_d::la_dlantb	(	character, intent(in)	norm,
		character, intent(in)	uplo,
		character, intent(in)	diag,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		real(dp), dimension(ldab,*), intent(in)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(*), intent(out)	work
	)

DLANTB: returns the value of the one norm, or the Frobenius norm, or the infinity norm, or the element of largest absolute value of an n by n triangular band matrix A, with ( k + 1 ) diagonals.

Here is the call graph for this function:

la_dlantp()

real(dp) function, public la_lapack_d::la_dlantp	(	character, intent(in)	norm,
		character, intent(in)	uplo,
		character, intent(in)	diag,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(in)	ap,
		real(dp), dimension(*), intent(out)	work
	)

DLANTP: returns the value of the one norm, or the Frobenius norm, or the infinity norm, or the element of largest absolute value of a triangular matrix A, supplied in packed form.

Here is the call graph for this function:

la_dlantr()

real(dp) function, public la_lapack_d::la_dlantr	(	character, intent(in)	norm,
		character, intent(in)	uplo,
		character, intent(in)	diag,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	work
	)

DLANTR: returns the value of the one norm, or the Frobenius norm, or the infinity norm, or the element of largest absolute value of a trapezoidal or triangular matrix A.

Here is the call graph for this function:

la_dlanv2()

pure subroutine, public la_lapack_d::la_dlanv2	(	real(dp), intent(inout)	a,
		real(dp), intent(inout)	b,
		real(dp), intent(inout)	c,
		real(dp), intent(inout)	d,
		real(dp), intent(out)	rt1r,
		real(dp), intent(out)	rt1i,
		real(dp), intent(out)	rt2r,
		real(dp), intent(out)	rt2i,
		real(dp), intent(out)	cs,
		real(dp), intent(out)	sn
	)

DLANV2: computes the Schur factorization of a real 2-by-2 nonsymmetric matrix in standard form: [ A B ] = [ CS -SN ] [ AA BB ] [ CS SN ] [ C D ] [ SN CS ] [ CC DD ] [-SN CS ] where either 1) CC = 0 so that AA and DD are real eigenvalues of the matrix, or 2) AA = DD and BB*CC < 0, so that AA + or - sqrt(BB*CC) are complex conjugate eigenvalues.

Here is the call graph for this function:

la_dlaorhr_col_getrfnp()

pure subroutine, public la_lapack_d::la_dlaorhr_col_getrfnp	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	d,
		integer(ilp), intent(out)	info
	)

DLAORHR_COL_GETRFNP: computes the modified LU factorization without pivoting of a real general M-by-N matrix A. The factorization has the form: A - S = L * U, where: S is a m-by-n diagonal sign matrix with the diagonal D, so that D(i) = S(i,i), 1 <= i <= min(M,N). The diagonal D is constructed as D(i)=-SIGN(A(i,i)), where A(i,i) is the value after performing i-1 steps of Gaussian elimination. This means that the diagonal element at each step of "modified" Gaussian elimination is at least one in absolute value (so that division-by-zero not not possible during the division by the diagonal element); L is a M-by-N lower triangular matrix with unit diagonal elements (lower trapezoidal if M > N); and U is a M-by-N upper triangular matrix (upper trapezoidal if M < N). This routine is an auxiliary routine used in the Householder reconstruction routine DORHR_COL. In DORHR_COL, this routine is applied to an M-by-N matrix A with orthonormal columns, where each element is bounded by one in absolute value. With the choice of the matrix S above, one can show that the diagonal element at each step of Gaussian elimination is the largest (in absolute value) in the column on or below the diagonal, so that no pivoting is required for numerical stability [1]. For more details on the Householder reconstruction algorithm, including the modified LU factorization, see [1]. This is the blocked right-looking version of the algorithm, calling Level 3 BLAS to update the submatrix. To factorize a block, this routine calls the recursive routine DLAORHR_COL_GETRFNP2. [1] "Reconstructing Householder vectors from tall-skinny QR", G. Ballard, J. Demmel, L. Grigori, M. Jacquelin, H.D. Nguyen, E. Solomonik, J. Parallel Distrib. Comput., vol. 85, pp. 3-31, 2015.

Here is the call graph for this function:

la_dlaorhr_col_getrfnp2()

pure recursive subroutine, public la_lapack_d::la_dlaorhr_col_getrfnp2	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	d,
		integer(ilp), intent(out)	info
	)

DLAORHR_COL_GETRFNP2: computes the modified LU factorization without pivoting of a real general M-by-N matrix A. The factorization has the form: A - S = L * U, where: S is a m-by-n diagonal sign matrix with the diagonal D, so that D(i) = S(i,i), 1 <= i <= min(M,N). The diagonal D is constructed as D(i)=-SIGN(A(i,i)), where A(i,i) is the value after performing i-1 steps of Gaussian elimination. This means that the diagonal element at each step of "modified" Gaussian elimination is at least one in absolute value (so that division-by-zero not possible during the division by the diagonal element); L is a M-by-N lower triangular matrix with unit diagonal elements (lower trapezoidal if M > N); and U is a M-by-N upper triangular matrix (upper trapezoidal if M < N). This routine is an auxiliary routine used in the Householder reconstruction routine DORHR_COL. In DORHR_COL, this routine is applied to an M-by-N matrix A with orthonormal columns, where each element is bounded by one in absolute value. With the choice of the matrix S above, one can show that the diagonal element at each step of Gaussian elimination is the largest (in absolute value) in the column on or below the diagonal, so that no pivoting is required for numerical stability [1]. For more details on the Householder reconstruction algorithm, including the modified LU factorization, see [1]. This is the recursive version of the LU factorization algorithm. Denote A - S by B. The algorithm divides the matrix B into four submatrices: [ B11 | B12 ] where B11 is n1 by n1, B = [ --—|--— ] B21 is (m-n1) by n1, [ B21 | B22 ] B12 is n1 by n2, B22 is (m-n1) by n2, with n1 = min(m,n)/2, n2 = n-n1. The subroutine calls itself to factor B11, solves for B21, solves for B12, updates B22, then calls itself to factor B22. For more details on the recursive LU algorithm, see [2]. DLAORHR_COL_GETRFNP2 is called to factorize a block by the blocked routine DLAORHR_COL_GETRFNP, which uses blocked code calling Level 3 BLAS to update the submatrix. However, DLAORHR_COL_GETRFNP2 is self-sufficient and can be used without DLAORHR_COL_GETRFNP. [1] "Reconstructing Householder vectors from tall-skinny QR", G. Ballard, J. Demmel, L. Grigori, M. Jacquelin, H.D. Nguyen, E. Solomonik, J. Parallel Distrib. Comput., vol. 85, pp. 3-31, 2015. [2] "Recursion leads to automatic variable blocking for dense linear algebra algorithms", F. Gustavson, IBM J. of Res. and Dev., vol. 41, no. 6, pp. 737-755, 1997.

Here is the call graph for this function:

la_dlapll()

pure subroutine, public la_lapack_d::la_dlapll	(	integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	x,
		integer(ilp), intent(in)	incx,
		real(dp), dimension(*), intent(inout)	y,
		integer(ilp), intent(in)	incy,
		real(dp), intent(out)	ssmin
	)

Given two column vectors X and Y, let A = ( X Y ). The subroutine first computes the QR factorization of A = Q*R, and then computes the SVD of the 2-by-2 upper triangular matrix R. The smaller singular value of R is returned in SSMIN, which is used as the measurement of the linear dependency of the vectors X and Y.

Here is the call graph for this function:

la_dlapmr()

pure subroutine, public la_lapack_d::la_dlapmr	(	logical(lk), intent(in)	forwrd,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(ldx,*), intent(inout)	x,
		integer(ilp), intent(in)	ldx,
		integer(ilp), dimension(*), intent(inout)	k
	)

DLAPMR: rearranges the rows of the M by N matrix X as specified by the permutation K(1),K(2),...,K(M) of the integers 1,...,M. If FORWRD = .TRUE., forward permutation: X(K(I),*) is moved X(I,*) for I = 1,2,...,M. If FORWRD = .FALSE., backward permutation: X(I,*) is moved to X(K(I),*) for I = 1,2,...,M.

la_dlapmt()

pure subroutine, public la_lapack_d::la_dlapmt	(	logical(lk), intent(in)	forwrd,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(ldx,*), intent(inout)	x,
		integer(ilp), intent(in)	ldx,
		integer(ilp), dimension(*), intent(inout)	k
	)

DLAPMT: rearranges the columns of the M by N matrix X as specified by the permutation K(1),K(2),...,K(N) of the integers 1,...,N. If FORWRD = .TRUE., forward permutation: X(*,K(J)) is moved X(*,J) for J = 1,2,...,N. If FORWRD = .FALSE., backward permutation: X(*,J) is moved to X(*,K(J)) for J = 1,2,...,N.

la_dlapy2()

pure real(dp) function, public la_lapack_d::la_dlapy2	(	real(dp), intent(in)	x,
		real(dp), intent(in)	y
	)

DLAPY2: returns sqrt(x**2+y**2), taking care not to cause unnecessary overflow and unnecessary underflow.

Here is the call graph for this function:

la_dlapy3()

pure real(dp) function, public la_lapack_d::la_dlapy3	(	real(dp), intent(in)	x,
		real(dp), intent(in)	y,
		real(dp), intent(in)	z
	)

DLAPY3: returns sqrt(x**2+y**2+z**2), taking care not to cause unnecessary overflow and unnecessary underflow.

Here is the call graph for this function:

la_dlaqgb()

pure subroutine, public la_lapack_d::la_dlaqgb	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kl,
		integer(ilp), intent(in)	ku,
		real(dp), dimension(ldab,*), intent(inout)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(*), intent(in)	r,
		real(dp), dimension(*), intent(in)	c,
		real(dp), intent(in)	rowcnd,
		real(dp), intent(in)	colcnd,
		real(dp), intent(in)	amax,
		character, intent(out)	equed
	)

DLAQGB: equilibrates a general M by N band matrix A with KL subdiagonals and KU superdiagonals using the row and scaling factors in the vectors R and C.

Here is the call graph for this function:

la_dlaqge()

pure subroutine, public la_lapack_d::la_dlaqge	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	r,
		real(dp), dimension(*), intent(in)	c,
		real(dp), intent(in)	rowcnd,
		real(dp), intent(in)	colcnd,
		real(dp), intent(in)	amax,
		character, intent(out)	equed
	)

DLAQGE: equilibrates a general M by N matrix A using the row and column scaling factors in the vectors R and C.

Here is the call graph for this function:

la_dlaqp2()

pure subroutine, public la_lapack_d::la_dlaqp2	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	offset,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(inout)	jpvt,
		real(dp), dimension(*), intent(out)	tau,
		real(dp), dimension(*), intent(inout)	vn1,
		real(dp), dimension(*), intent(inout)	vn2,
		real(dp), dimension(*), intent(out)	work
	)

DLAQP2: computes a QR factorization with column pivoting of the block A(OFFSET+1:M,1:N). The block A(1:OFFSET,1:N) is accordingly pivoted, but not factorized.

Here is the call graph for this function:

la_dlaqps()

pure subroutine, public la_lapack_d::la_dlaqps	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	offset,
		integer(ilp), intent(in)	nb,
		integer(ilp), intent(out)	kb,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(inout)	jpvt,
		real(dp), dimension(*), intent(out)	tau,
		real(dp), dimension(*), intent(inout)	vn1,
		real(dp), dimension(*), intent(inout)	vn2,
		real(dp), dimension(*), intent(inout)	auxv,
		real(dp), dimension(ldf,*), intent(inout)	f,
		integer(ilp), intent(in)	ldf
	)

DLAQPS: computes a step of QR factorization with column pivoting of a real M-by-N matrix A by using Blas-3. It tries to factorize NB columns from A starting from the row OFFSET+1, and updates all of the matrix with Blas-3 xGEMM. In some cases, due to catastrophic cancellations, it cannot factorize NB columns. Hence, the actual number of factorized columns is returned in KB. Block A(1:OFFSET,1:N) is accordingly pivoted, but not factorized.

Here is the call graph for this function:

la_dlaqr0()

subroutine, public la_lapack_d::la_dlaqr0	(	logical(lk), intent(in)	wantt,
		logical(lk), intent(in)	wantz,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ilo,
		integer(ilp), intent(in)	ihi,
		real(dp), dimension(ldh,*), intent(inout)	h,
		integer(ilp), intent(in)	ldh,
		real(dp), dimension(*), intent(out)	wr,
		real(dp), dimension(*), intent(out)	wi,
		integer(ilp), intent(in)	iloz,
		integer(ilp), intent(in)	ihiz,
		real(dp), dimension(ldz,*), intent(inout)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DLAQR0: computes the eigenvalues of a Hessenberg matrix H and, optionally, the matrices T and Z from the Schur decomposition H = Z T Z**T, where T is an upper quasi-triangular matrix (the Schur form), and Z is the orthogonal matrix of Schur vectors. Optionally Z may be postmultiplied into an input orthogonal matrix Q so that this routine can give the Schur factorization of a matrix A which has been reduced to the Hessenberg form H by the orthogonal matrix Q: A = Q*H*Q**T = (QZ)*T*(QZ)**T.

Here is the call graph for this function:

la_dlaqr1()

pure subroutine, public la_lapack_d::la_dlaqr1	(	integer(ilp), intent(in)	n,
		real(dp), dimension(ldh,*), intent(in)	h,
		integer(ilp), intent(in)	ldh,
		real(dp), intent(in)	sr1,
		real(dp), intent(in)	si1,
		real(dp), intent(in)	sr2,
		real(dp), intent(in)	si2,
		real(dp), dimension(*), intent(out)	v
	)

Given a 2-by-2 or 3-by-3 matrix H, DLAQR1: sets v to a scalar multiple of the first column of the product (*) K = (H - (sr1 + i*si1)*I)*(H - (sr2 + i*si2)*I) scaling to avoid overflows and most underflows. It is assumed that either 1) sr1 = sr2 and si1 = -si2 or 2) si1 = si2 = 0. This is useful for starting double implicit shift bulges in the QR algorithm.

la_dlaqr2()

subroutine, public la_lapack_d::la_dlaqr2	(	logical(lk), intent(in)	wantt,
		logical(lk), intent(in)	wantz,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ktop,
		integer(ilp), intent(in)	kbot,
		integer(ilp), intent(in)	nw,
		real(dp), dimension(ldh,*), intent(inout)	h,
		integer(ilp), intent(in)	ldh,
		integer(ilp), intent(in)	iloz,
		integer(ilp), intent(in)	ihiz,
		real(dp), dimension(ldz,*), intent(inout)	z,
		integer(ilp), intent(in)	ldz,
		integer(ilp), intent(out)	ns,
		integer(ilp), intent(out)	nd,
		real(dp), dimension(*), intent(out)	sr,
		real(dp), dimension(*), intent(out)	si,
		real(dp), dimension(ldv,*), intent(out)	v,
		integer(ilp), intent(in)	ldv,
		integer(ilp), intent(in)	nh,
		real(dp), dimension(ldt,*), intent(out)	t,
		integer(ilp), intent(in)	ldt,
		integer(ilp), intent(in)	nv,
		real(dp), dimension(ldwv,*), intent(out)	wv,
		integer(ilp), intent(in)	ldwv,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork
	)

DLAQR2: is identical to DLAQR3 except that it avoids recursion by calling DLAHQR instead of DLAQR4. Aggressive early deflation: This subroutine accepts as input an upper Hessenberg matrix H and performs an orthogonal similarity transformation designed to detect and deflate fully converged eigenvalues from a trailing principal submatrix. On output H has been over- written by a new Hessenberg matrix that is a perturbation of an orthogonal similarity transformation of H. It is to be hoped that the final version of H has many zero subdiagonal entries.

Here is the call graph for this function:

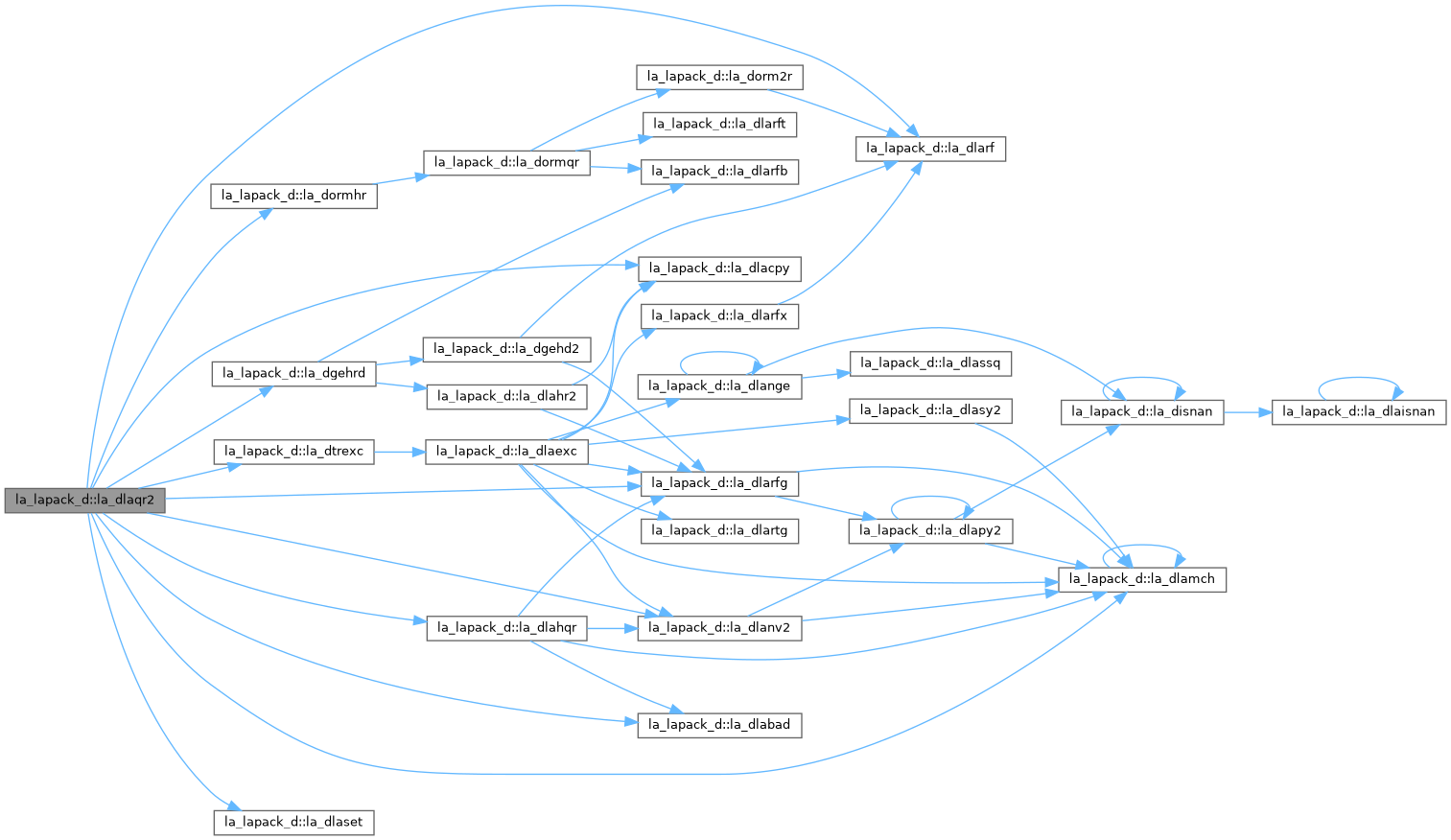
la_dlaqr3()

subroutine, public la_lapack_d::la_dlaqr3	(	logical(lk), intent(in)	wantt,
		logical(lk), intent(in)	wantz,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ktop,
		integer(ilp), intent(in)	kbot,
		integer(ilp), intent(in)	nw,
		real(dp), dimension(ldh,*), intent(inout)	h,
		integer(ilp), intent(in)	ldh,
		integer(ilp), intent(in)	iloz,
		integer(ilp), intent(in)	ihiz,
		real(dp), dimension(ldz,*), intent(inout)	z,
		integer(ilp), intent(in)	ldz,
		integer(ilp), intent(out)	ns,
		integer(ilp), intent(out)	nd,
		real(dp), dimension(*), intent(out)	sr,
		real(dp), dimension(*), intent(out)	si,
		real(dp), dimension(ldv,*), intent(out)	v,
		integer(ilp), intent(in)	ldv,
		integer(ilp), intent(in)	nh,
		real(dp), dimension(ldt,*), intent(out)	t,
		integer(ilp), intent(in)	ldt,
		integer(ilp), intent(in)	nv,
		real(dp), dimension(ldwv,*), intent(out)	wv,
		integer(ilp), intent(in)	ldwv,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork
	)

Aggressive early deflation: DLAQR3: accepts as input an upper Hessenberg matrix H and performs an orthogonal similarity transformation designed to detect and deflate fully converged eigenvalues from a trailing principal submatrix. On output H has been over- written by a new Hessenberg matrix that is a perturbation of an orthogonal similarity transformation of H. It is to be hoped that the final version of H has many zero subdiagonal entries.

Here is the call graph for this function:

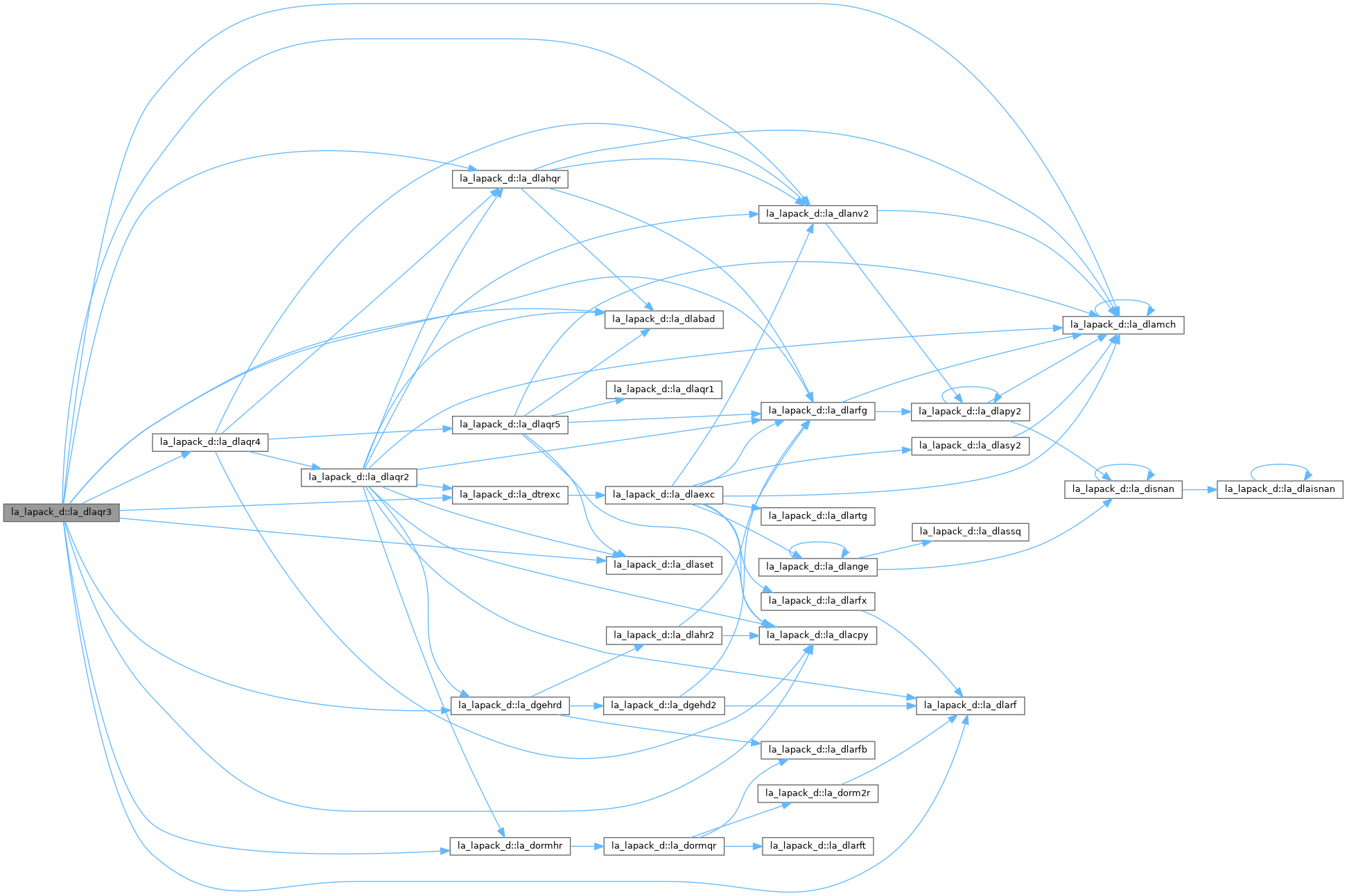
la_dlaqr4()

subroutine, public la_lapack_d::la_dlaqr4	(	logical(lk), intent(in)	wantt,
		logical(lk), intent(in)	wantz,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ilo,
		integer(ilp), intent(in)	ihi,
		real(dp), dimension(ldh,*), intent(inout)	h,
		integer(ilp), intent(in)	ldh,
		real(dp), dimension(*), intent(out)	wr,
		real(dp), dimension(*), intent(out)	wi,
		integer(ilp), intent(in)	iloz,
		integer(ilp), intent(in)	ihiz,
		real(dp), dimension(ldz,*), intent(inout)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DLAQR4: implements one level of recursion for DLAQR0. It is a complete implementation of the small bulge multi-shift QR algorithm. It may be called by DLAQR0 and, for large enough deflation window size, it may be called by DLAQR3. This subroutine is identical to DLAQR0 except that it calls DLAQR2 instead of DLAQR3. DLAQR4 computes the eigenvalues of a Hessenberg matrix H and, optionally, the matrices T and Z from the Schur decomposition H = Z T Z**T, where T is an upper quasi-triangular matrix (the Schur form), and Z is the orthogonal matrix of Schur vectors. Optionally Z may be postmultiplied into an input orthogonal matrix Q so that this routine can give the Schur factorization of a matrix A which has been reduced to the Hessenberg form H by the orthogonal matrix Q: A = Q*H*Q**T = (QZ)*T*(QZ)**T.

Here is the call graph for this function:

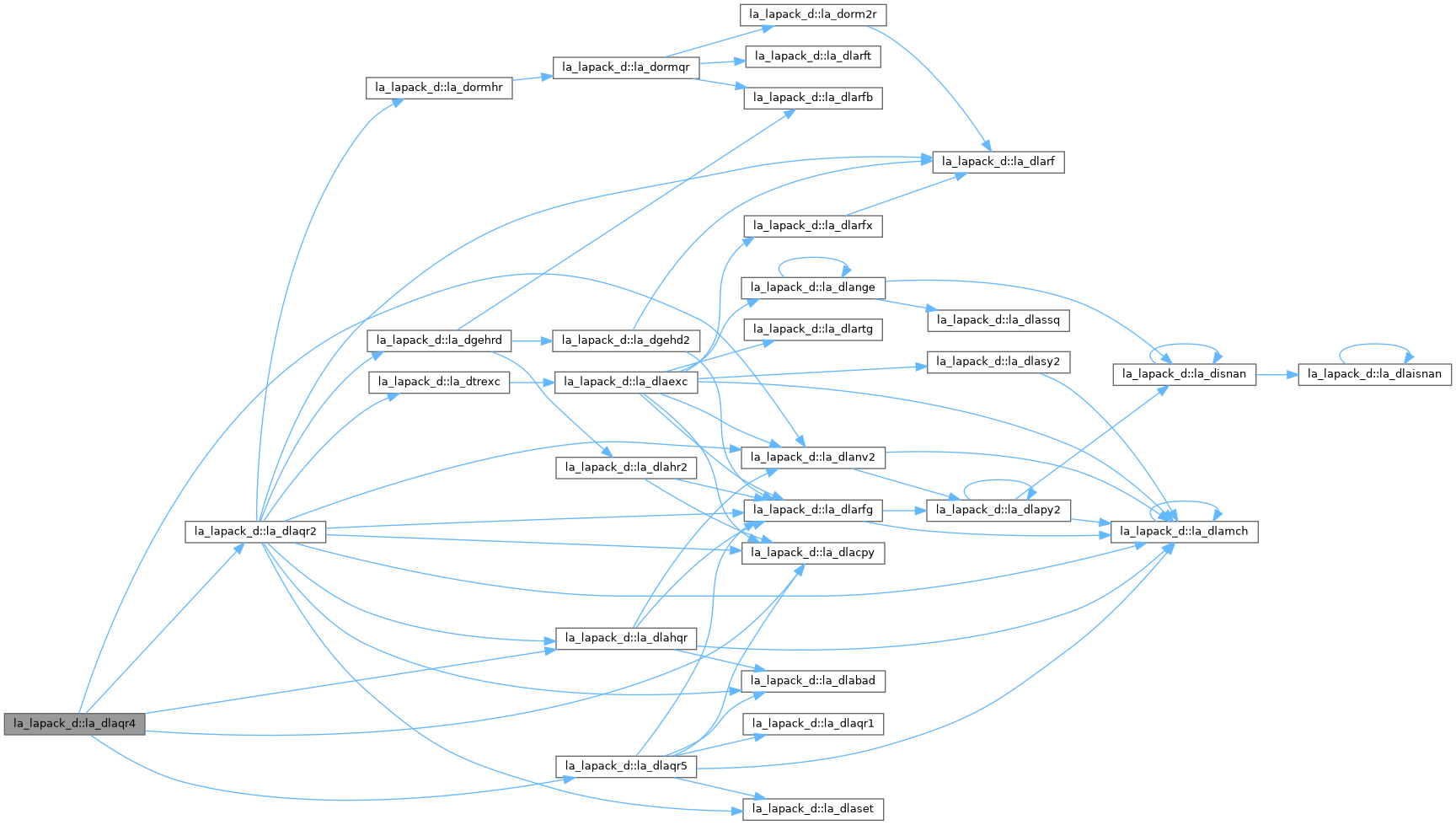
la_dlaqr5()

pure subroutine, public la_lapack_d::la_dlaqr5	(	logical(lk), intent(in)	wantt,
		logical(lk), intent(in)	wantz,
		integer(ilp), intent(in)	kacc22,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ktop,
		integer(ilp), intent(in)	kbot,
		integer(ilp), intent(in)	nshfts,
		real(dp), dimension(*), intent(inout)	sr,
		real(dp), dimension(*), intent(inout)	si,
		real(dp), dimension(ldh,*), intent(inout)	h,
		integer(ilp), intent(in)	ldh,
		integer(ilp), intent(in)	iloz,
		integer(ilp), intent(in)	ihiz,
		real(dp), dimension(ldz,*), intent(inout)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(ldv,*), intent(out)	v,
		integer(ilp), intent(in)	ldv,
		real(dp), dimension(ldu,*), intent(out)	u,
		integer(ilp), intent(in)	ldu,
		integer(ilp), intent(in)	nv,
		real(dp), dimension(ldwv,*), intent(out)	wv,
		integer(ilp), intent(in)	ldwv,
		integer(ilp), intent(in)	nh,
		real(dp), dimension(ldwh,*), intent(out)	wh,
		integer(ilp), intent(in)	ldwh
	)

DLAQR5:, called by DLAQR0, performs a single small-bulge multi-shift QR sweep.

Here is the call graph for this function:

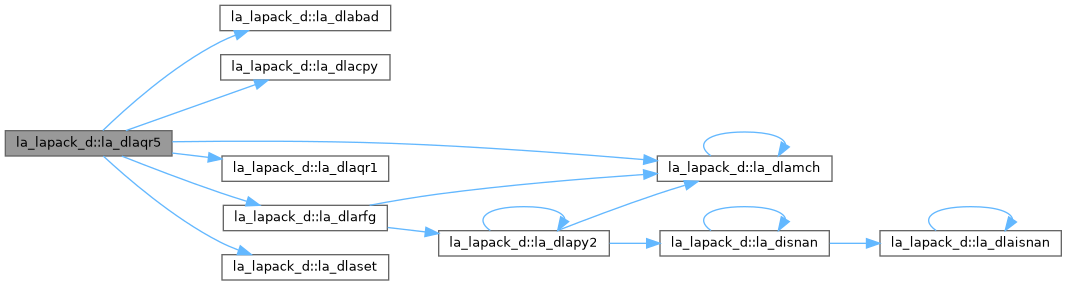
la_dlaqsb()

pure subroutine, public la_lapack_d::la_dlaqsb	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kd,
		real(dp), dimension(ldab,*), intent(inout)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(*), intent(in)	s,
		real(dp), intent(in)	scond,
		real(dp), intent(in)	amax,
		character, intent(out)	equed
	)

DLAQSB: equilibrates a symmetric band matrix A using the scaling factors in the vector S.

Here is the call graph for this function:

la_dlaqsp()

pure subroutine, public la_lapack_d::la_dlaqsp	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	ap,
		real(dp), dimension(*), intent(in)	s,
		real(dp), intent(in)	scond,
		real(dp), intent(in)	amax,
		character, intent(out)	equed
	)

DLAQSP: equilibrates a symmetric matrix A using the scaling factors in the vector S.

Here is the call graph for this function:

la_dlaqsy()

pure subroutine, public la_lapack_d::la_dlaqsy	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	s,
		real(dp), intent(in)	scond,
		real(dp), intent(in)	amax,
		character, intent(out)	equed
	)

DLAQSY: equilibrates a symmetric matrix A using the scaling factors in the vector S.

Here is the call graph for this function:

la_dlaqtr()

subroutine, public la_lapack_d::la_dlaqtr	(	logical(lk), intent(in)	ltran,
		logical(lk), intent(in)	lreal,
		integer(ilp), intent(in)	n,
		real(dp), dimension(ldt,*), intent(in)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(*), intent(in)	b,
		real(dp), intent(in)	w,
		real(dp), intent(out)	scale,
		real(dp), dimension(*), intent(inout)	x,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DLAQTR: solves the real quasi-triangular system op(T)*p = scale*c, if LREAL = .TRUE. or the complex quasi-triangular systems op(T + iB)*(p+iq) = scale*(c+id), if LREAL = .FALSE. in real arithmetic, where T is upper quasi-triangular. If LREAL = .FALSE., then the first diagonal block of T must be 1 by 1, B is the specially structured matrix B = [ b(1) b(2) ... b(n) ] [ w ] [ w ] [ . ] [ w ] op(A) = A or A**T, A**T denotes the transpose of matrix A. On input, X = [ c ]. On output, X = [ p ]. [ d ] [ q ] This subroutine is designed for the condition number estimation in routine DTRSNA.

Here is the call graph for this function:

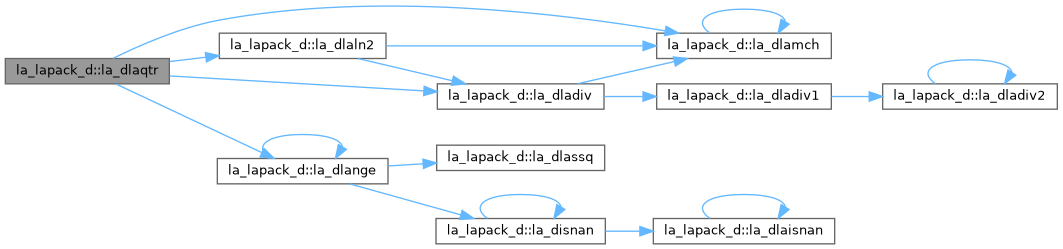
la_dlaqz0()

recursive subroutine, public la_lapack_d::la_dlaqz0	(	character, intent(in)	wants,
		character, intent(in)	wantq,
		character, intent(in)	wantz,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ilo,
		integer(ilp), intent(in)	ihi,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension( *), intent(inout)	alphar,
		real(dp), dimension(*), intent(inout)	alphai,
		real(dp), dimension(*), intent(inout)	beta,
		real(dp), dimension(ldq,*), intent(inout)	q,
		integer(ilp), intent(in)	ldq,
		real(dp), dimension(ldz,*), intent(inout)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(inout)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(in)	rec,
		integer(ilp), intent(out)	info
	)

DLAQZ0: computes the eigenvalues of a real matrix pair (H,T), where H is an upper Hessenberg matrix and T is upper triangular, using the double-shift QZ method. Matrix pairs of this type are produced by the reduction to generalized upper Hessenberg form of a real matrix pair (A,B): A = Q1*H*Z1**T, B = Q1*T*Z1**T, as computed by DGGHRD. If JOB='S', then the Hessenberg-triangular pair (H,T) is also reduced to generalized Schur form, H = Q*S*Z**T, T = Q*P*Z**T, where Q and Z are orthogonal matrices, P is an upper triangular matrix, and S is a quasi-triangular matrix with 1-by-1 and 2-by-2 diagonal blocks. The 1-by-1 blocks correspond to real eigenvalues of the matrix pair (H,T) and the 2-by-2 blocks correspond to complex conjugate pairs of eigenvalues. Additionally, the 2-by-2 upper triangular diagonal blocks of P corresponding to 2-by-2 blocks of S are reduced to positive diagonal form, i.e., if S(j+1,j) is non-zero, then P(j+1,j) = P(j,j+1) = 0, P(j,j) > 0, and P(j+1,j+1) > 0. Optionally, the orthogonal matrix Q from the generalized Schur factorization may be postmultiplied into an input matrix Q1, and the orthogonal matrix Z may be postmultiplied into an input matrix Z1. If Q1 and Z1 are the orthogonal matrices from DGGHRD that reduced the matrix pair (A,B) to generalized upper Hessenberg form, then the output matrices Q1*Q and Z1*Z are the orthogonal factors from the generalized Schur factorization of (A,B): A = (Q1*Q)*S*(Z1*Z)**T, B = (Q1*Q)*P*(Z1*Z)**T. To avoid overflow, eigenvalues of the matrix pair (H,T) (equivalently, of (A,B)) are computed as a pair of values (alpha,beta), where alpha is complex and beta real. If beta is nonzero, lambda = alpha / beta is an eigenvalue of the generalized nonsymmetric eigenvalue problem (GNEP) A*x = lambda*B*x and if alpha is nonzero, mu = beta / alpha is an eigenvalue of the alternate form of the GNEP mu*A*y = B*y. Real eigenvalues can be read directly from the generalized Schur form: alpha = S(i,i), beta = P(i,i). Ref: C.B. Moler Eigenvalue Problems", SIAM J. Numer. Anal., 10(1973), pp. 241&ndash;256. Ref: B. Kagstrom, D. Kressner, "Multishift Variants of the QZ Algorithm with Aggressive Early Deflation", SIAM J. Numer. Anal., 29(2006), pp. 199&ndash;227. Ref: T. Steel, D. Camps, K. Meerbergen, R. Vandebril "A multishift, multipole rational QZ method with agressive early deflation".

Here is the call graph for this function:

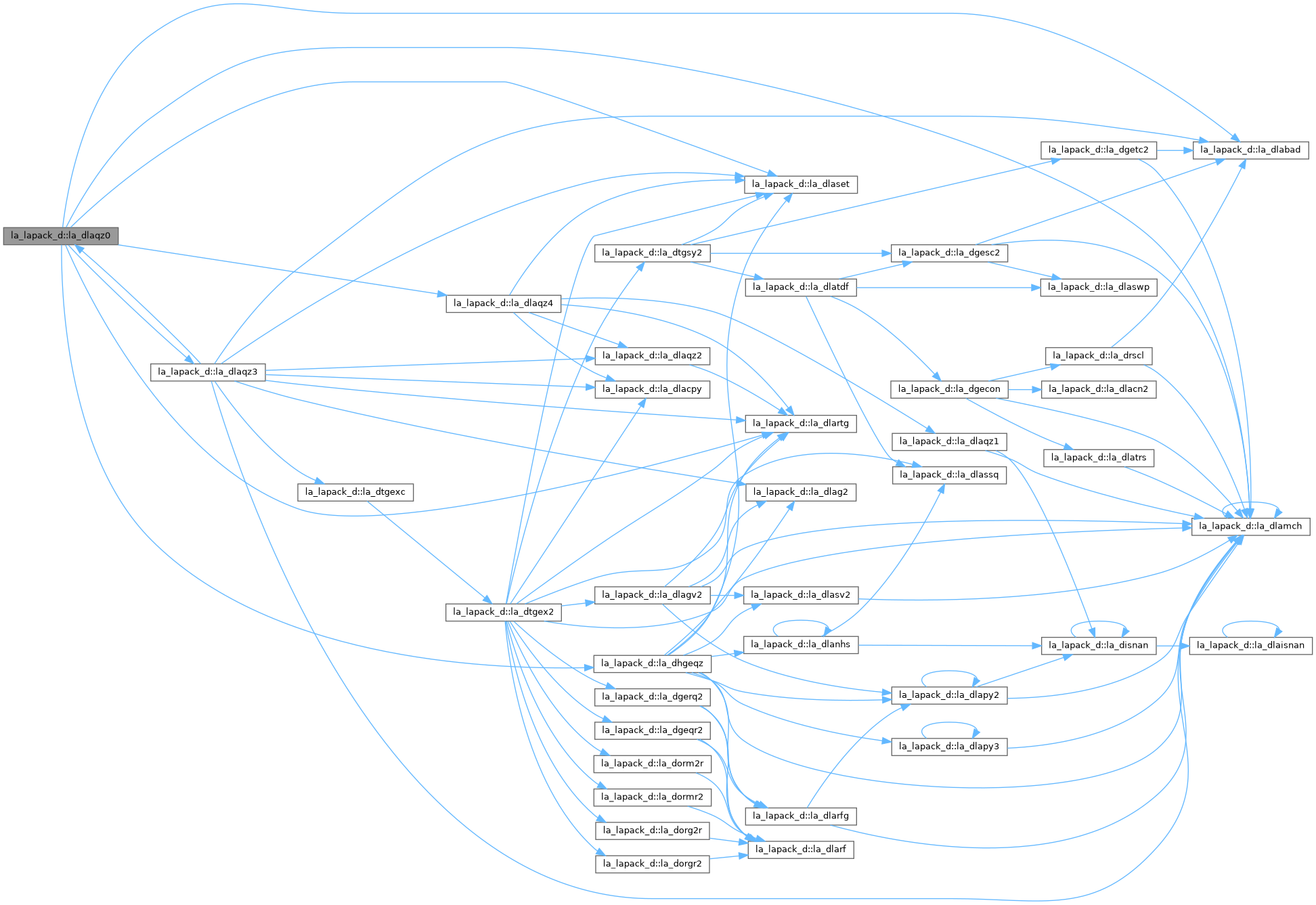
la_dlaqz1()

pure subroutine, public la_lapack_d::la_dlaqz1	(	real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), intent(in)	sr1,
		real(dp), intent(in)	sr2,
		real(dp), intent(in)	si,
		real(dp), intent(in)	beta1,
		real(dp), intent(in)	beta2,
		real(dp), dimension(*), intent(out)	v
	)

Given a 3-by-3 matrix pencil (A,B), DLAQZ1: sets v to a scalar multiple of the first column of the product (*) K = (A - (beta2*sr2 - i*si)*B)*B^(-1)*(beta1*A - (sr2 + i*si2)*B)*B^(-1). It is assumed that either 1) sr1 = sr2 or 2) si = 0. This is useful for starting double implicit shift bulges in the QZ algorithm.

Here is the call graph for this function:

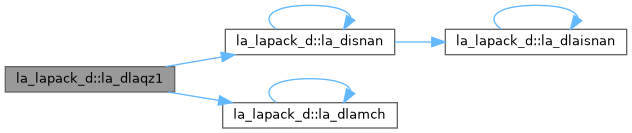
la_dlaqz2()

pure subroutine, public la_lapack_d::la_dlaqz2	(	logical(lk), intent(in)	ilq,
		logical(lk), intent(in)	ilz,
		integer(ilp), intent(in)	k,
		integer(ilp), intent(in)	istartm,
		integer(ilp), intent(in)	istopm,
		integer(ilp), intent(in)	ihi,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(in)	nq,
		integer(ilp), intent(in)	qstart,
		real(dp), dimension(ldq,*), intent(inout)	q,
		integer(ilp), intent(in)	ldq,
		integer(ilp), intent(in)	nz,
		integer(ilp), intent(in)	zstart,
		real(dp), dimension(ldz,*), intent(inout)	z,
		integer(ilp), intent(in)	ldz
	)

DLAQZ2: chases a 2x2 shift bulge in a matrix pencil down a single position.

Here is the call graph for this function:

la_dlaqz3()

recursive subroutine, public la_lapack_d::la_dlaqz3	(	logical(lk), intent(in)	ilschur,
		logical(lk), intent(in)	ilq,
		logical(lk), intent(in)	ilz,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ilo,
		integer(ilp), intent(in)	ihi,
		integer(ilp), intent(in)	nw,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldq,*), intent(inout)	q,
		integer(ilp), intent(in)	ldq,
		real(dp), dimension(ldz,*), intent(inout)	z,
		integer(ilp), intent(in)	ldz,
		integer(ilp), intent(out)	ns,
		integer(ilp), intent(out)	nd,
		real(dp), dimension( *), intent(inout)	alphar,
		real(dp), dimension(*), intent(inout)	alphai,
		real(dp), dimension(*), intent(inout)	beta,
		real(dp), dimension(ldqc,*), intent(inout)	qc,
		integer(ilp), intent(in)	ldqc,
		real(dp), dimension(ldzc,*), intent(inout)	zc,
		integer(ilp), intent(in)	ldzc,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(in)	rec,
		integer(ilp), intent(out)	info
	)

DLAQZ3: performs AED.

Here is the call graph for this function:

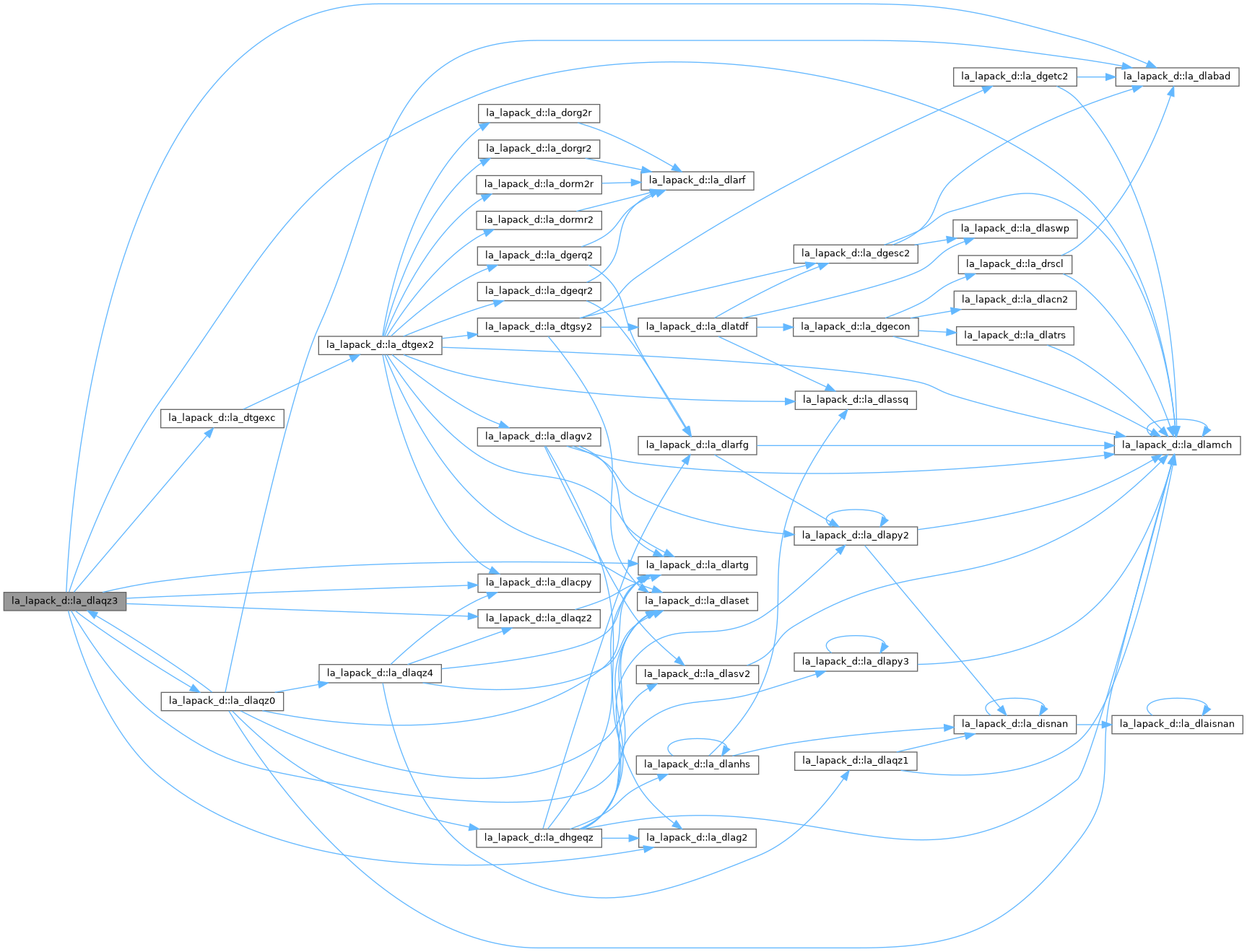
la_dlaqz4()

pure subroutine, public la_lapack_d::la_dlaqz4	(	logical(lk), intent(in)	ilschur,
		logical(lk), intent(in)	ilq,
		logical(lk), intent(in)	ilz,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ilo,
		integer(ilp), intent(in)	ihi,
		integer(ilp), intent(in)	nshifts,
		integer(ilp), intent(in)	nblock_desired,
		real(dp), dimension(*), intent(inout)	sr,
		real(dp), dimension(*), intent(inout)	si,
		real(dp), dimension(*), intent(inout)	ss,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldq,*), intent(inout)	q,
		integer(ilp), intent(in)	ldq,
		real(dp), dimension(ldz,*), intent(inout)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension( ldqc,*), intent(inout)	qc,
		integer(ilp), intent(in)	ldqc,
		real(dp), dimension(ldzc,*), intent(inout)	zc,
		integer(ilp), intent(in)	ldzc,
		real(dp), dimension(*), intent(inout)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DLAQZ4: Executes a single multishift QZ sweep.

Here is the call graph for this function:

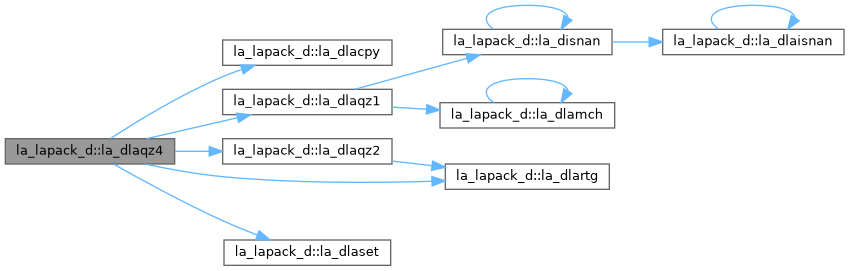
la_dlar1v()

pure subroutine, public la_lapack_d::la_dlar1v	(	integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	b1,
		integer(ilp), intent(in)	bn,
		real(dp), intent(in)	lambda,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(in)	l,
		real(dp), dimension(*), intent(in)	ld,
		real(dp), dimension(*), intent(in)	lld,
		real(dp), intent(in)	pivmin,
		real(dp), intent(in)	gaptol,
		real(dp), dimension(*), intent(inout)	z,
		logical(lk), intent(in)	wantnc,
		integer(ilp), intent(out)	negcnt,
		real(dp), intent(out)	ztz,
		real(dp), intent(out)	mingma,
		integer(ilp), intent(inout)	r,
		integer(ilp), dimension(*), intent(out)	isuppz,
		real(dp), intent(out)	nrminv,
		real(dp), intent(out)	resid,
		real(dp), intent(out)	rqcorr,
		real(dp), dimension(*), intent(out)	work
	)

DLAR1V: computes the (scaled) r-th column of the inverse of the sumbmatrix in rows B1 through BN of the tridiagonal matrix L D L**T - sigma I. When sigma is close to an eigenvalue, the computed vector is an accurate eigenvector. Usually, r corresponds to the index where the eigenvector is largest in magnitude. The following steps accomplish this computation : (a) Stationary qd transform, L D L**T - sigma I = L(+) D(+) L(+)**T, (b) Progressive qd transform, L D L**T - sigma I = U(-) D(-) U(-)**T, (c) Computation of the diagonal elements of the inverse of L D L**T - sigma I by combining the above transforms, and choosing r as the index where the diagonal of the inverse is (one of the) largest in magnitude. (d) Computation of the (scaled) r-th column of the inverse using the twisted factorization obtained by combining the top part of the the stationary and the bottom part of the progressive transform.

Here is the call graph for this function:

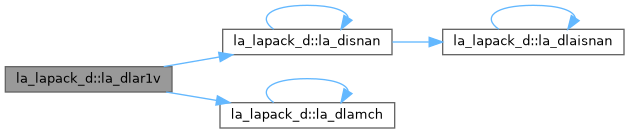
la_dlar2v()

pure subroutine, public la_lapack_d::la_dlar2v	(	integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	x,
		real(dp), dimension(*), intent(inout)	y,
		real(dp), dimension(*), intent(inout)	z,
		integer(ilp), intent(in)	incx,
		real(dp), dimension(*), intent(in)	c,
		real(dp), dimension(*), intent(in)	s,
		integer(ilp), intent(in)	incc
	)

DLAR2V: applies a vector of real plane rotations from both sides to a sequence of 2-by-2 real symmetric matrices, defined by the elements of the vectors x, y and z. For i = 1,2,...,n ( x(i) z(i) ) := ( c(i) s(i) ) ( x(i) z(i) ) ( c(i) -s(i) ) ( z(i) y(i) ) ( -s(i) c(i) ) ( z(i) y(i) ) ( s(i) c(i) )

la_dlarf()

pure subroutine, public la_lapack_d::la_dlarf	(	character, intent(in)	side,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(in)	v,
		integer(ilp), intent(in)	incv,
		real(dp), intent(in)	tau,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work
	)

DLARF: applies a real elementary reflector H to a real m by n matrix C, from either the left or the right. H is represented in the form H = I - tau * v * v**T where tau is a real scalar and v is a real vector. If tau = 0, then H is taken to be the unit matrix.

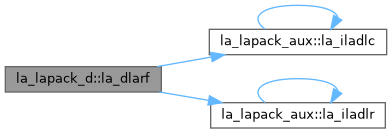
la_dlarfb()

pure subroutine, public la_lapack_d::la_dlarfb	(	character, intent(in)	side,
		character, intent(in)	trans,
		character, intent(in)	direct,
		character, intent(in)	storev,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		real(dp), dimension(ldv,*), intent(in)	v,
		integer(ilp), intent(in)	ldv,
		real(dp), dimension(ldt,*), intent(in)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(ldwork,*), intent(out)	work,
		integer(ilp), intent(in)	ldwork
	)

DLARFB: applies a real block reflector H or its transpose H**T to a real m by n matrix C, from either the left or the right.

la_dlarfb_gett()

pure subroutine, public la_lapack_d::la_dlarfb_gett	(	character, intent(in)	ident,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		real(dp), dimension(ldt,*), intent(in)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldwork,*), intent(out)	work,
		integer(ilp), intent(in)	ldwork
	)

DLARFB_GETT: applies a real Householder block reflector H from the left to a real (K+M)-by-N "triangular-pentagonal" matrix composed of two block matrices: an upper trapezoidal K-by-N matrix A stored in the array A, and a rectangular M-by-(N-K) matrix B, stored in the array B. The block reflector H is stored in a compact WY-representation, where the elementary reflectors are in the arrays A, B and T. See Further Details section.

la_dlarfg()

pure subroutine, public la_lapack_d::la_dlarfg	(	integer(ilp), intent(in)	n,
		real(dp), intent(inout)	alpha,
		real(dp), dimension(*), intent(inout)	x,
		integer(ilp), intent(in)	incx,
		real(dp), intent(out)	tau
	)

DLARFG: generates a real elementary reflector H of order n, such that H * ( alpha ) = ( beta ), H**T * H = I. ( x ) ( 0 ) where alpha and beta are scalars, and x is an (n-1)-element real vector. H is represented in the form H = I - tau * ( 1 ) * ( 1 v**T ) , ( v ) where tau is a real scalar and v is a real (n-1)-element vector. If the elements of x are all zero, then tau = 0 and H is taken to be the unit matrix. Otherwise 1 <= tau <= 2.

Here is the call graph for this function:

la_dlarfgp()

subroutine, public la_lapack_d::la_dlarfgp	(	integer(ilp), intent(in)	n,
		real(dp), intent(inout)	alpha,
		real(dp), dimension(*), intent(inout)	x,
		integer(ilp), intent(in)	incx,
		real(dp), intent(out)	tau
	)

DLARFGP: generates a real elementary reflector H of order n, such that H * ( alpha ) = ( beta ), H**T * H = I. ( x ) ( 0 ) where alpha and beta are scalars, beta is non-negative, and x is an (n-1)-element real vector. H is represented in the form H = I - tau * ( 1 ) * ( 1 v**T ) , ( v ) where tau is a real scalar and v is a real (n-1)-element vector. If the elements of x are all zero, then tau = 0 and H is taken to be the unit matrix.

Here is the call graph for this function:

la_dlarft()

pure subroutine, public la_lapack_d::la_dlarft	(	character, intent(in)	direct,
		character, intent(in)	storev,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		real(dp), dimension(ldv,*), intent(in)	v,
		integer(ilp), intent(in)	ldv,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(ldt,*), intent(out)	t,
		integer(ilp), intent(in)	ldt
	)

DLARFT: forms the triangular factor T of a real block reflector H of order n, which is defined as a product of k elementary reflectors. If DIRECT = 'F', H = H(1) H(2) . . . H(k) and T is upper triangular; If DIRECT = 'B', H = H(k) . . . H(2) H(1) and T is lower triangular. If STOREV = 'C', the vector which defines the elementary reflector H(i) is stored in the i-th column of the array V, and H = I - V * T * V**T If STOREV = 'R', the vector which defines the elementary reflector H(i) is stored in the i-th row of the array V, and H = I - V**T * T * V.

la_dlarfx()

pure subroutine, public la_lapack_d::la_dlarfx	(	character, intent(in)	side,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(in)	v,
		real(dp), intent(in)	tau,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work
	)

DLARFX: applies a real elementary reflector H to a real m by n matrix C, from either the left or the right. H is represented in the form H = I - tau * v * v**T where tau is a real scalar and v is a real vector. If tau = 0, then H is taken to be the unit matrix This version uses inline code if H has order < 11.

Here is the call graph for this function:

la_dlarfy()

pure subroutine, public la_lapack_d::la_dlarfy	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(in)	v,
		integer(ilp), intent(in)	incv,
		real(dp), intent(in)	tau,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work
	)

DLARFY: applies an elementary reflector, or Householder matrix, H, to an n x n symmetric matrix C, from both the left and the right. H is represented in the form H = I - tau * v * v' where tau is a scalar and v is a vector. If tau is zero, then H is taken to be the unit matrix.

la_dlargv()

pure subroutine, public la_lapack_d::la_dlargv	(	integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	x,
		integer(ilp), intent(in)	incx,
		real(dp), dimension(*), intent(inout)	y,
		integer(ilp), intent(in)	incy,
		real(dp), dimension(*), intent(out)	c,
		integer(ilp), intent(in)	incc
	)

DLARGV: generates a vector of real plane rotations, determined by elements of the real vectors x and y. For i = 1,2,...,n ( c(i) s(i) ) ( x(i) ) = ( a(i) ) ( -s(i) c(i) ) ( y(i) ) = ( 0 )

la_dlarnv()

pure subroutine, public la_lapack_d::la_dlarnv	(	integer(ilp), intent(in)	idist,
		integer(ilp), dimension(4), intent(inout)	iseed,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(out)	x
	)

DLARNV: returns a vector of n random real numbers from a uniform or normal distribution.

Here is the call graph for this function:

la_dlarra()

pure subroutine, public la_lapack_d::la_dlarra	(	integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(inout)	e,
		real(dp), dimension(*), intent(inout)	e2,
		real(dp), intent(in)	spltol,
		real(dp), intent(in)	tnrm,
		integer(ilp), intent(out)	nsplit,
		integer(ilp), dimension(*), intent(out)	isplit,
		integer(ilp), intent(out)	info
	)

Compute the splitting points with threshold SPLTOL. DLARRA: sets any "small" off-diagonal elements to zero.

la_dlarrb()

pure subroutine, public la_lapack_d::la_dlarrb	(	integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(in)	lld,
		integer(ilp), intent(in)	ifirst,
		integer(ilp), intent(in)	ilast,
		real(dp), intent(in)	rtol1,
		real(dp), intent(in)	rtol2,
		integer(ilp), intent(in)	offset,
		real(dp), dimension(*), intent(inout)	w,
		real(dp), dimension(*), intent(inout)	wgap,
		real(dp), dimension(*), intent(inout)	werr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		real(dp), intent(in)	pivmin,
		real(dp), intent(in)	spdiam,
		integer(ilp), intent(in)	twist,
		integer(ilp), intent(out)	info
	)

Given the relatively robust representation(RRR) L D L^T, DLARRB: does "limited" bisection to refine the eigenvalues of L D L^T, W( IFIRST-OFFSET ) through W( ILAST-OFFSET ), to more accuracy. Initial guesses for these eigenvalues are input in W, the corresponding estimate of the error in these guesses and their gaps are input in WERR and WGAP, respectively. During bisection, intervals [left, right] are maintained by storing their mid-points and semi-widths in the arrays W and WERR respectively.

Here is the call graph for this function:

la_dlarrc()

pure subroutine, public la_lapack_d::la_dlarrc	(	character, intent(in)	jobt,
		integer(ilp), intent(in)	n,
		real(dp), intent(in)	vl,
		real(dp), intent(in)	vu,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(in)	e,
		real(dp), intent(in)	pivmin,
		integer(ilp), intent(out)	eigcnt,
		integer(ilp), intent(out)	lcnt,
		integer(ilp), intent(out)	rcnt,
		integer(ilp), intent(out)	info
	)

Find the number of eigenvalues of the symmetric tridiagonal matrix T that are in the interval (VL,VU] if JOBT = 'T', and of L D L^T if JOBT = 'L'.

la_dlarrd()

pure subroutine, public la_lapack_d::la_dlarrd	(	character, intent(in)	range,
		character, intent(in)	order,
		integer(ilp), intent(in)	n,
		real(dp), intent(in)	vl,
		real(dp), intent(in)	vu,
		integer(ilp), intent(in)	il,
		integer(ilp), intent(in)	iu,
		real(dp), dimension(*), intent(in)	gers,
		real(dp), intent(in)	reltol,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(in)	e,
		real(dp), dimension(*), intent(in)	e2,
		real(dp), intent(in)	pivmin,
		integer(ilp), intent(in)	nsplit,
		integer(ilp), dimension(*), intent(in)	isplit,
		integer(ilp), intent(out)	m,
		real(dp), dimension(*), intent(out)	w,
		real(dp), dimension(*), intent(out)	werr,
		real(dp), intent(out)	wl,
		real(dp), intent(out)	wu,
		integer(ilp), dimension(*), intent(out)	iblock,
		integer(ilp), dimension(*), intent(out)	indexw,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DLARRD: computes the eigenvalues of a symmetric tridiagonal matrix T to suitable accuracy. This is an auxiliary code to be called from DSTEMR. The user may ask for all eigenvalues, all eigenvalues in the half-open interval (VL, VU], or the IL-th through IU-th eigenvalues. To avoid overflow, the matrix must be scaled so that its largest element is no greater than overflow**(1/2) * underflow**(1/4) in absolute value, and for greatest accuracy, it should not be much smaller than that. See W. Kahan "Accurate Eigenvalues of a Symmetric Tridiagonal Matrix", Report CS41, Computer Science Dept., Stanford University, July 21, 1966.

Here is the call graph for this function:

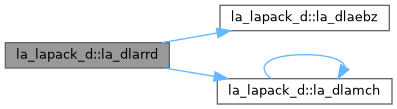
la_dlarre()

pure subroutine, public la_lapack_d::la_dlarre	(	character, intent(in)	range,
		integer(ilp), intent(in)	n,
		real(dp), intent(inout)	vl,
		real(dp), intent(inout)	vu,
		integer(ilp), intent(in)	il,
		integer(ilp), intent(in)	iu,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(inout)	e,
		real(dp), dimension(*), intent(inout)	e2,
		real(dp), intent(in)	rtol1,
		real(dp), intent(in)	rtol2,
		real(dp), intent(in)	spltol,
		integer(ilp), intent(out)	nsplit,
		integer(ilp), dimension(*), intent(out)	isplit,
		integer(ilp), intent(out)	m,
		real(dp), dimension(*), intent(out)	w,
		real(dp), dimension(*), intent(out)	werr,
		real(dp), dimension(*), intent(out)	wgap,
		integer(ilp), dimension(*), intent(out)	iblock,
		integer(ilp), dimension(*), intent(out)	indexw,
		real(dp), dimension(*), intent(out)	gers,
		real(dp), intent(out)	pivmin,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

To find the desired eigenvalues of a given real symmetric tridiagonal matrix T, DLARRE: sets any "small" off-diagonal elements to zero, and for each unreduced block T_i, it finds (a) a suitable shift at one end of the block's spectrum, (b) the base representation, T_i - sigma_i I = L_i D_i L_i^T, and (c) eigenvalues of each L_i D_i L_i^T. The representations and eigenvalues found are then used by DSTEMR to compute the eigenvectors of T. The accuracy varies depending on whether bisection is used to find a few eigenvalues or the dqds algorithm (subroutine DLASQ2) to conpute all and then discard any unwanted one. As an added benefit, DLARRE also outputs the n Gerschgorin intervals for the matrices L_i D_i L_i^T.

Here is the call graph for this function:

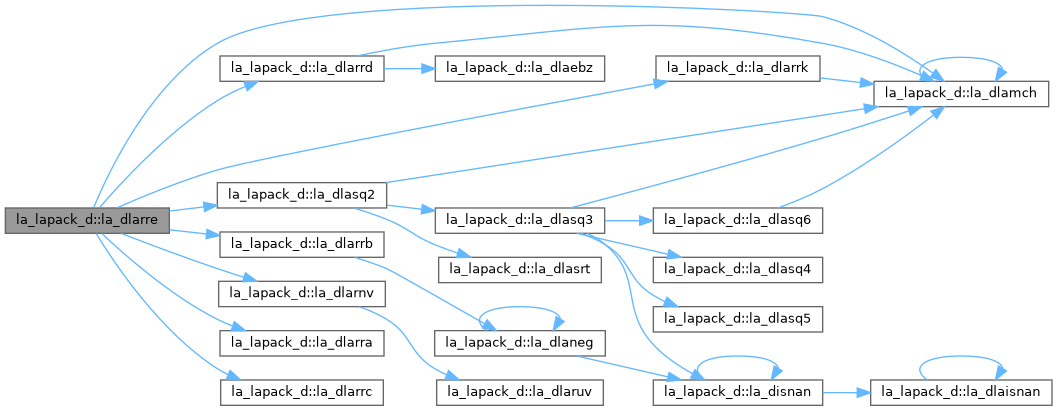
la_dlarrf()

pure subroutine, public la_lapack_d::la_dlarrf	(	integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(in)	l,
		real(dp), dimension(*), intent(in)	ld,
		integer(ilp), intent(in)	clstrt,
		integer(ilp), intent(in)	clend,
		real(dp), dimension(*), intent(in)	w,
		real(dp), dimension(*), intent(inout)	wgap,
		real(dp), dimension(*), intent(in)	werr,
		real(dp), intent(in)	spdiam,
		real(dp), intent(in)	clgapl,
		real(dp), intent(in)	clgapr,
		real(dp), intent(in)	pivmin,
		real(dp), intent(out)	sigma,
		real(dp), dimension(*), intent(out)	dplus,
		real(dp), dimension(*), intent(out)	lplus,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

Given the initial representation L D L^T and its cluster of close eigenvalues (in a relative measure), W( CLSTRT ), W( CLSTRT+1 ), ... W( CLEND ), DLARRF: finds a new relatively robust representation L D L^T - SIGMA I = L(+) D(+) L(+)^T such that at least one of the eigenvalues of L(+) D(+) L(+)^T is relatively isolated.

Here is the call graph for this function:

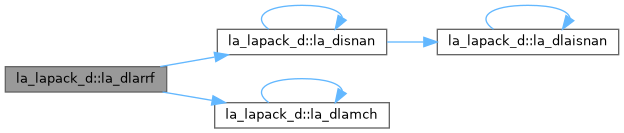
la_dlarrj()

pure subroutine, public la_lapack_d::la_dlarrj	(	integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(in)	e2,
		integer(ilp), intent(in)	ifirst,
		integer(ilp), intent(in)	ilast,
		real(dp), intent(in)	rtol,
		integer(ilp), intent(in)	offset,
		real(dp), dimension(*), intent(inout)	w,
		real(dp), dimension(*), intent(inout)	werr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		real(dp), intent(in)	pivmin,
		real(dp), intent(in)	spdiam,
		integer(ilp), intent(out)	info
	)

Given the initial eigenvalue approximations of T, DLARRJ: does bisection to refine the eigenvalues of T, W( IFIRST-OFFSET ) through W( ILAST-OFFSET ), to more accuracy. Initial guesses for these eigenvalues are input in W, the corresponding estimate of the error in these guesses in WERR. During bisection, intervals [left, right] are maintained by storing their mid-points and semi-widths in the arrays W and WERR respectively.

la_dlarrk()

pure subroutine, public la_lapack_d::la_dlarrk	(	integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	iw,
		real(dp), intent(in)	gl,
		real(dp), intent(in)	gu,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(in)	e2,
		real(dp), intent(in)	pivmin,
		real(dp), intent(in)	reltol,
		real(dp), intent(out)	w,
		real(dp), intent(out)	werr,
		integer(ilp), intent(out)	info
	)

DLARRK: computes one eigenvalue of a symmetric tridiagonal matrix T to suitable accuracy. This is an auxiliary code to be called from DSTEMR. To avoid overflow, the matrix must be scaled so that its largest element is no greater than overflow**(1/2) * underflow**(1/4) in absolute value, and for greatest accuracy, it should not be much smaller than that. See W. Kahan "Accurate Eigenvalues of a Symmetric Tridiagonal Matrix", Report CS41, Computer Science Dept., Stanford University, July 21, 1966.

Here is the call graph for this function:

la_dlarrr()

pure subroutine, public la_lapack_d::la_dlarrr	(	integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(inout)	e,
		integer(ilp), intent(out)	info
	)

Perform tests to decide whether the symmetric tridiagonal matrix T warrants expensive computations which guarantee high relative accuracy in the eigenvalues.

Here is the call graph for this function:

la_dlarrv()

pure subroutine, public la_lapack_d::la_dlarrv	(	integer(ilp), intent(in)	n,
		real(dp), intent(in)	vl,
		real(dp), intent(in)	vu,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(inout)	l,
		real(dp), intent(in)	pivmin,
		integer(ilp), dimension(*), intent(in)	isplit,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	dol,
		integer(ilp), intent(in)	dou,
		real(dp), intent(in)	minrgp,
		real(dp), intent(inout)	rtol1,
		real(dp), intent(inout)	rtol2,
		real(dp), dimension(*), intent(inout)	w,
		real(dp), dimension(*), intent(inout)	werr,
		real(dp), dimension(*), intent(inout)	wgap,
		integer(ilp), dimension(*), intent(in)	iblock,
		integer(ilp), dimension(*), intent(in)	indexw,
		real(dp), dimension(*), intent(in)	gers,
		real(dp), dimension(ldz,*), intent(out)	z,
		integer(ilp), intent(in)	ldz,
		integer(ilp), dimension(*), intent(out)	isuppz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DLARRV: computes the eigenvectors of the tridiagonal matrix T = L D L**T given L, D and APPROXIMATIONS to the eigenvalues of L D L**T. The input eigenvalues should have been computed by DLARRE.

Here is the call graph for this function:

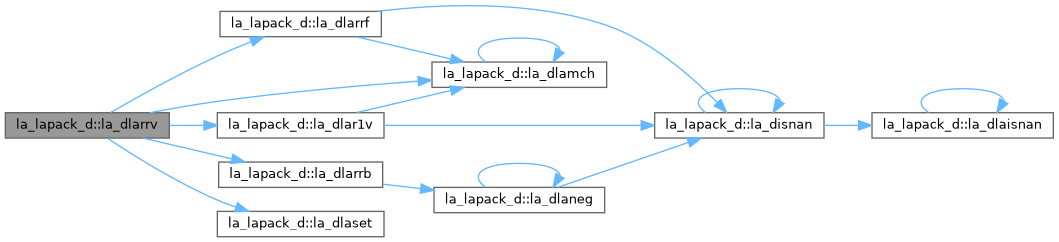
la_dlartg()

pure subroutine, public la_lapack_d::la_dlartg	(	real(dp), intent(in)	f,
		real(dp), intent(in)	g,
		real(dp), intent(out)	c,
		real(dp), intent(out)	s,
		real(dp), intent(out)	r
	)

!

DLARTG: generates a plane rotation so that [ C S ] . [ F ] = [ R ] [ -S C ] [ G ] [ 0 ] where C**2 + S**2 = 1. The mathematical formulas used for C and S are R = sign(F) * sqrt(F**2 + G**2) C = F / R S = G / R Hence C >= 0. The algorithm used to compute these quantities incorporates scaling to avoid overflow or underflow in computing the square root of the sum of squares. This version is discontinuous in R at F = 0 but it returns the same C and S as ZLARTG for complex inputs (F,0) and (G,0). This is a more accurate version of the BLAS1 routine DROTG, with the following other differences: F and G are unchanged on return. If G=0, then C=1 and S=0. If F=0 and (G .ne. 0), then C=0 and S=sign(1,G) without doing any floating point operations (saves work in DBDSQR when there are zeros on the diagonal). If F exceeds G in magnitude, C will be positive. Below, wp=>dp stands for double precision from LA_CONSTANTS module.

la_dlartgp()

pure subroutine, public la_lapack_d::la_dlartgp	(	real(dp), intent(in)	f,
		real(dp), intent(in)	g,
		real(dp), intent(out)	cs,
		real(dp), intent(out)	sn,
		real(dp), intent(out)	r
	)

DLARTGP: generates a plane rotation so that [ CS SN ] . [ F ] = [ R ] where CS**2 + SN**2 = 1. [ -SN CS ] [ G ] [ 0 ] This is a slower, more accurate version of the Level 1 BLAS routine DROTG, with the following other differences: F and G are unchanged on return. If G=0, then CS=(+/-)1 and SN=0. If F=0 and (G .ne. 0), then CS=0 and SN=(+/-)1. The sign is chosen so that R >= 0.

Here is the call graph for this function:

la_dlartgs()

pure subroutine, public la_lapack_d::la_dlartgs	(	real(dp), intent(in)	x,
		real(dp), intent(in)	y,
		real(dp), intent(in)	sigma,
		real(dp), intent(out)	cs,
		real(dp), intent(out)	sn
	)

DLARTGS: generates a plane rotation designed to introduce a bulge in Golub-Reinsch-style implicit QR iteration for the bidiagonal SVD problem. X and Y are the top-row entries, and SIGMA is the shift. The computed CS and SN define a plane rotation satisfying [ CS SN ] . [ X^2 - SIGMA ] = [ R ], [ -SN CS ] [ X * Y ] [ 0 ] with R nonnegative. If X^2 - SIGMA and X * Y are 0, then the rotation is by PI/2.

Here is the call graph for this function:

la_dlartv()

pure subroutine, public la_lapack_d::la_dlartv	(	integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	x,
		integer(ilp), intent(in)	incx,
		real(dp), dimension(*), intent(inout)	y,
		integer(ilp), intent(in)	incy,
		real(dp), dimension(*), intent(in)	c,
		real(dp), dimension(*), intent(in)	s,
		integer(ilp), intent(in)	incc
	)

DLARTV: applies a vector of real plane rotations to elements of the real vectors x and y. For i = 1,2,...,n ( x(i) ) := ( c(i) s(i) ) ( x(i) ) ( y(i) ) ( -s(i) c(i) ) ( y(i) )

la_dlaruv()

pure subroutine, public la_lapack_d::la_dlaruv	(	integer(ilp), dimension(4), intent(inout)	iseed,
		integer(ilp), intent(in)	n,
		real(dp), dimension(n), intent(out)	x
	)

DLARUV: returns a vector of n random real numbers from a uniform (0,1) distribution (n <= 128). This is an auxiliary routine called by DLARNV and ZLARNV.

la_dlarz()

pure subroutine, public la_lapack_d::la_dlarz	(	character, intent(in)	side,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	l,
		real(dp), dimension(*), intent(in)	v,
		integer(ilp), intent(in)	incv,
		real(dp), intent(in)	tau,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work
	)

DLARZ: applies a real elementary reflector H to a real M-by-N matrix C, from either the left or the right. H is represented in the form H = I - tau * v * v**T where tau is a real scalar and v is a real vector. If tau = 0, then H is taken to be the unit matrix. H is a product of k elementary reflectors as returned by DTZRZF.

la_dlarzb()

pure subroutine, public la_lapack_d::la_dlarzb	(	character, intent(in)	side,
		character, intent(in)	trans,
		character, intent(in)	direct,
		character, intent(in)	storev,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		integer(ilp), intent(in)	l,
		real(dp), dimension(ldv,*), intent(inout)	v,
		integer(ilp), intent(in)	ldv,
		real(dp), dimension(ldt,*), intent(inout)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(ldwork,*), intent(out)	work,
		integer(ilp), intent(in)	ldwork
	)

DLARZB: applies a real block reflector H or its transpose H**T to a real distributed M-by-N C from the left or the right. Currently, only STOREV = 'R' and DIRECT = 'B' are supported.

la_dlarzt()

pure subroutine, public la_lapack_d::la_dlarzt	(	character, intent(in)	direct,
		character, intent(in)	storev,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		real(dp), dimension(ldv,*), intent(inout)	v,
		integer(ilp), intent(in)	ldv,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(ldt,*), intent(out)	t,
		integer(ilp), intent(in)	ldt
	)

DLARZT: forms the triangular factor T of a real block reflector H of order > n, which is defined as a product of k elementary reflectors. If DIRECT = 'F', H = H(1) H(2) . . . H(k) and T is upper triangular; If DIRECT = 'B', H = H(k) . . . H(2) H(1) and T is lower triangular. If STOREV = 'C', the vector which defines the elementary reflector H(i) is stored in the i-th column of the array V, and H = I - V * T * V**T If STOREV = 'R', the vector which defines the elementary reflector H(i) is stored in the i-th row of the array V, and H = I - V**T * T * V Currently, only STOREV = 'R' and DIRECT = 'B' are supported.

la_dlas2()

pure subroutine, public la_lapack_d::la_dlas2	(	real(dp), intent(in)	f,
		real(dp), intent(in)	g,
		real(dp), intent(in)	h,
		real(dp), intent(out)	ssmin,
		real(dp), intent(out)	ssmax
	)

DLAS2: computes the singular values of the 2-by-2 matrix [ F G ] [ 0 H ]. On return, SSMIN is the smaller singular value and SSMAX is the larger singular value.

la_dlascl()

pure subroutine, public la_lapack_d::la_dlascl	(	character, intent(in)	type,
		integer(ilp), intent(in)	kl,
		integer(ilp), intent(in)	ku,
		real(dp), intent(in)	cfrom,
		real(dp), intent(in)	cto,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), intent(out)	info
	)

DLASCL: multiplies the M by N real matrix A by the real scalar CTO/CFROM. This is done without over/underflow as long as the final result CTO*A(I,J)/CFROM does not over/underflow. TYPE specifies that A may be full, upper triangular, lower triangular, upper Hessenberg, or banded.

Here is the call graph for this function:

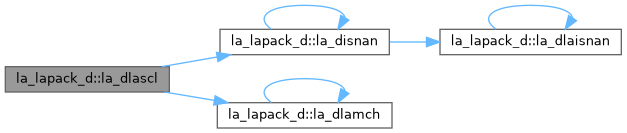
la_dlasd0()

pure subroutine, public la_lapack_d::la_dlasd0	(	integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	sqre,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(inout)	e,
		real(dp), dimension(ldu,*), intent(out)	u,
		integer(ilp), intent(in)	ldu,
		real(dp), dimension(ldvt,*), intent(out)	vt,
		integer(ilp), intent(in)	ldvt,
		integer(ilp), intent(in)	smlsiz,
		integer(ilp), dimension(*), intent(out)	iwork,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

Using a divide and conquer approach, DLASD0: computes the singular value decomposition (SVD) of a real upper bidiagonal N-by-M matrix B with diagonal D and offdiagonal E, where M = N + SQRE. The algorithm computes orthogonal matrices U and VT such that B = U * S * VT. The singular values S are overwritten on D. A related subroutine, DLASDA, computes only the singular values, and optionally, the singular vectors in compact form.

Here is the call graph for this function:

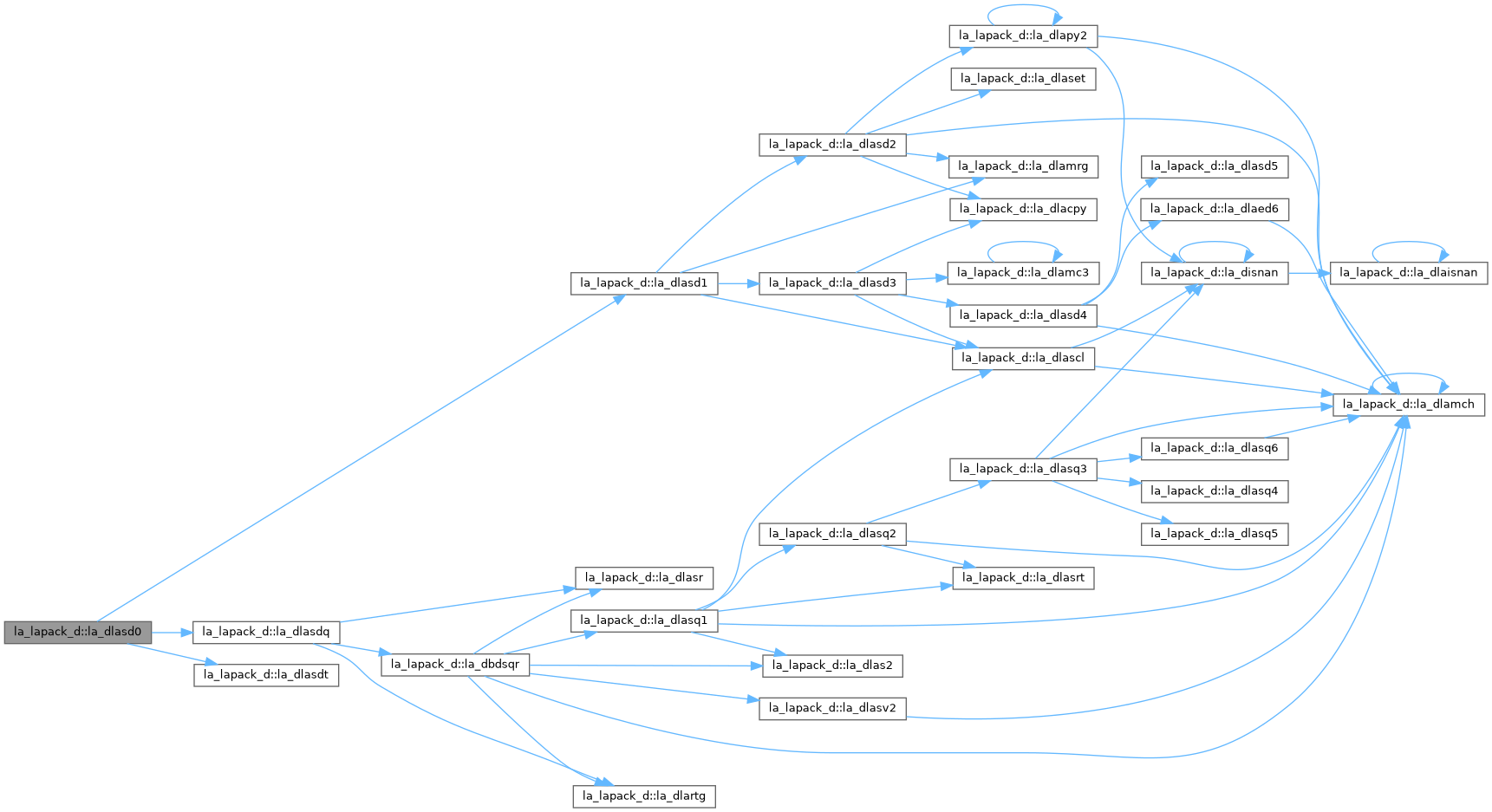
la_dlasd1()

pure subroutine, public la_lapack_d::la_dlasd1	(	integer(ilp), intent(in)	nl,
		integer(ilp), intent(in)	nr,
		integer(ilp), intent(in)	sqre,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), intent(inout)	alpha,
		real(dp), intent(inout)	beta,
		real(dp), dimension(ldu,*), intent(inout)	u,
		integer(ilp), intent(in)	ldu,
		real(dp), dimension(ldvt,*), intent(inout)	vt,
		integer(ilp), intent(in)	ldvt,
		integer(ilp), dimension(*), intent(inout)	idxq,
		integer(ilp), dimension(*), intent(out)	iwork,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DLASD1: computes the SVD of an upper bidiagonal N-by-M matrix B, where N = NL + NR + 1 and M = N + SQRE. DLASD1 is called from DLASD0. A related subroutine DLASD7 handles the case in which the singular values (and the singular vectors in factored form) are desired. DLASD1 computes the SVD as follows: ( D1(in) 0 0 0 ) B = U(in) * ( Z1**T a Z2**T b ) * VT(in) ( 0 0 D2(in) 0 ) = U(out) * ( D(out) 0) * VT(out) where Z**T = (Z1**T a Z2**T b) = u**T VT**T, and u is a vector of dimension M with ALPHA and BETA in the NL+1 and NL+2 th entries and zeros elsewhere; and the entry b is empty if SQRE = 0. The left singular vectors of the original matrix are stored in U, and the transpose of the right singular vectors are stored in VT, and the singular values are in D. The algorithm consists of three stages: The first stage consists of deflating the size of the problem when there are multiple singular values or when there are zeros in the Z vector. For each such occurrence the dimension of the secular equation problem is reduced by one. This stage is performed by the routine DLASD2. The second stage consists of calculating the updated singular values. This is done by finding the square roots of the roots of the secular equation via the routine DLASD4 (as called by DLASD3). This routine also calculates the singular vectors of the current problem. The final stage consists of computing the updated singular vectors directly using the updated singular values. The singular vectors for the current problem are multiplied with the singular vectors from the overall problem.

Here is the call graph for this function:

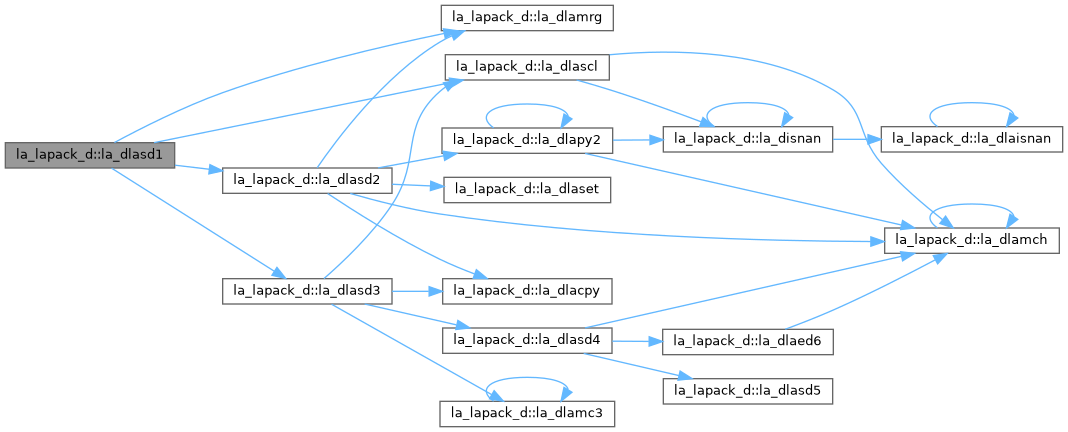
la_dlasd2()

pure subroutine, public la_lapack_d::la_dlasd2	(	integer(ilp), intent(in)	nl,
		integer(ilp), intent(in)	nr,
		integer(ilp), intent(in)	sqre,
		integer(ilp), intent(out)	k,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(out)	z,
		real(dp), intent(in)	alpha,
		real(dp), intent(in)	beta,
		real(dp), dimension(ldu,*), intent(inout)	u,
		integer(ilp), intent(in)	ldu,
		real(dp), dimension(ldvt,*), intent(inout)	vt,
		integer(ilp), intent(in)	ldvt,
		real(dp), dimension(*), intent(out)	dsigma,
		real(dp), dimension(ldu2,*), intent(out)	u2,
		integer(ilp), intent(in)	ldu2,
		real(dp), dimension(ldvt2,*), intent(out)	vt2,
		integer(ilp), intent(in)	ldvt2,
		integer(ilp), dimension(*), intent(out)	idxp,
		integer(ilp), dimension(*), intent(out)	idx,
		integer(ilp), dimension(*), intent(out)	idxc,
		integer(ilp), dimension(*), intent(inout)	idxq,
		integer(ilp), dimension(*), intent(out)	coltyp,
		integer(ilp), intent(out)	info
	)

DLASD2: merges the two sets of singular values together into a single sorted set. Then it tries to deflate the size of the problem. There are two ways in which deflation can occur: when two or more singular values are close together or if there is a tiny entry in the Z vector. For each such occurrence the order of the related secular equation problem is reduced by one. DLASD2 is called from DLASD1.

Here is the call graph for this function:

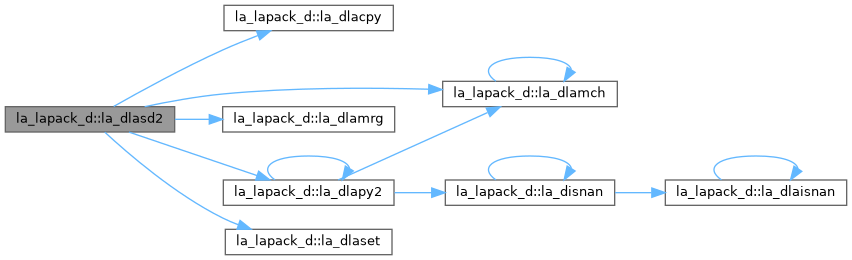
la_dlasd3()

pure subroutine, public la_lapack_d::la_dlasd3	(	integer(ilp), intent(in)	nl,
		integer(ilp), intent(in)	nr,
		integer(ilp), intent(in)	sqre,
		integer(ilp), intent(in)	k,
		real(dp), dimension(*), intent(out)	d,
		real(dp), dimension(ldq,*), intent(out)	q,
		integer(ilp), intent(in)	ldq,
		real(dp), dimension(*), intent(inout)	dsigma,
		real(dp), dimension(ldu,*), intent(out)	u,
		integer(ilp), intent(in)	ldu,
		real(dp), dimension(ldu2,*), intent(in)	u2,
		integer(ilp), intent(in)	ldu2,
		real(dp), dimension(ldvt,*), intent(out)	vt,
		integer(ilp), intent(in)	ldvt,
		real(dp), dimension(ldvt2,*), intent(inout)	vt2,
		integer(ilp), intent(in)	ldvt2,
		integer(ilp), dimension(*), intent(in)	idxc,
		integer(ilp), dimension(*), intent(in)	ctot,
		real(dp), dimension(*), intent(inout)	z,
		integer(ilp), intent(out)	info
	)

DLASD3: finds all the square roots of the roots of the secular equation, as defined by the values in D and Z. It makes the appropriate calls to DLASD4 and then updates the singular vectors by matrix multiplication. This code makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray XMP, Cray YMP, Cray C 90, or Cray 2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none. DLASD3 is called from DLASD1.

Here is the call graph for this function:

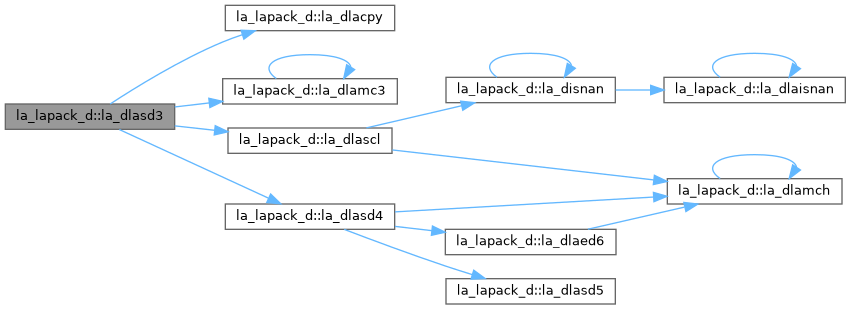
la_dlasd4()

pure subroutine, public la_lapack_d::la_dlasd4	(	integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	i,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(in)	z,
		real(dp), dimension(*), intent(out)	delta,
		real(dp), intent(in)	rho,
		real(dp), intent(out)	sigma,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

This subroutine computes the square root of the I-th updated eigenvalue of a positive symmetric rank-one modification to a positive diagonal matrix whose entries are given as the squares of the corresponding entries in the array d, and that 0 <= D(i) < D(j) for i < j and that RHO > 0. This is arranged by the calling routine, and is no loss in generality. The rank-one modified system is thus diag( D ) * diag( D ) + RHO * Z * Z_transpose. where we assume the Euclidean norm of Z is 1. The method consists of approximating the rational functions in the secular equation by simpler interpolating rational functions.

Here is the call graph for this function:

la_dlasd5()

pure subroutine, public la_lapack_d::la_dlasd5	(	integer(ilp), intent(in)	i,
		real(dp), dimension(2), intent(in)	d,
		real(dp), dimension(2), intent(in)	z,
		real(dp), dimension(2), intent(out)	delta,
		real(dp), intent(in)	rho,
		real(dp), intent(out)	dsigma,
		real(dp), dimension(2), intent(out)	work
	)

This subroutine computes the square root of the I-th eigenvalue of a positive symmetric rank-one modification of a 2-by-2 diagonal matrix diag( D ) * diag( D ) + RHO * Z * transpose(Z) . The diagonal entries in the array D are assumed to satisfy 0 <= D(i) < D(j) for i < j . We also assume RHO > 0 and that the Euclidean norm of the vector Z is one.

la_dlasd6()

pure subroutine, public la_lapack_d::la_dlasd6	(	integer(ilp), intent(in)	icompq,
		integer(ilp), intent(in)	nl,
		integer(ilp), intent(in)	nr,
		integer(ilp), intent(in)	sqre,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(inout)	vf,
		real(dp), dimension(*), intent(inout)	vl,
		real(dp), intent(inout)	alpha,
		real(dp), intent(inout)	beta,
		integer(ilp), dimension(*), intent(inout)	idxq,
		integer(ilp), dimension(*), intent(out)	perm,
		integer(ilp), intent(out)	givptr,
		integer(ilp), dimension(ldgcol,*), intent(out)	givcol,
		integer(ilp), intent(in)	ldgcol,
		real(dp), dimension(ldgnum,*), intent(out)	givnum,
		integer(ilp), intent(in)	ldgnum,
		real(dp), dimension(ldgnum,*), intent(out)	poles,
		real(dp), dimension(*), intent(out)	difl,
		real(dp), dimension(*), intent(out)	difr,
		real(dp), dimension(*), intent(out)	z,
		integer(ilp), intent(out)	k,
		real(dp), intent(out)	c,
		real(dp), intent(out)	s,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DLASD6: computes the SVD of an updated upper bidiagonal matrix B obtained by merging two smaller ones by appending a row. This routine is used only for the problem which requires all singular values and optionally singular vector matrices in factored form. B is an N-by-M matrix with N = NL + NR + 1 and M = N + SQRE. A related subroutine, DLASD1, handles the case in which all singular values and singular vectors of the bidiagonal matrix are desired. DLASD6 computes the SVD as follows: ( D1(in) 0 0 0 ) B = U(in) * ( Z1**T a Z2**T b ) * VT(in) ( 0 0 D2(in) 0 ) = U(out) * ( D(out) 0) * VT(out) where Z**T = (Z1**T a Z2**T b) = u**T VT**T, and u is a vector of dimension M with ALPHA and BETA in the NL+1 and NL+2 th entries and zeros elsewhere; and the entry b is empty if SQRE = 0. The singular values of B can be computed using D1, D2, the first components of all the right singular vectors of the lower block, and the last components of all the right singular vectors of the upper block. These components are stored and updated in VF and VL, respectively, in DLASD6. Hence U and VT are not explicitly referenced. The singular values are stored in D. The algorithm consists of two stages: The first stage consists of deflating the size of the problem when there are multiple singular values or if there is a zero in the Z vector. For each such occurrence the dimension of the secular equation problem is reduced by one. This stage is performed by the routine DLASD7. The second stage consists of calculating the updated singular values. This is done by finding the roots of the secular equation via the routine DLASD4 (as called by DLASD8). This routine also updates VF and VL and computes the distances between the updated singular values and the old singular values. DLASD6 is called from DLASDA.

Here is the call graph for this function:

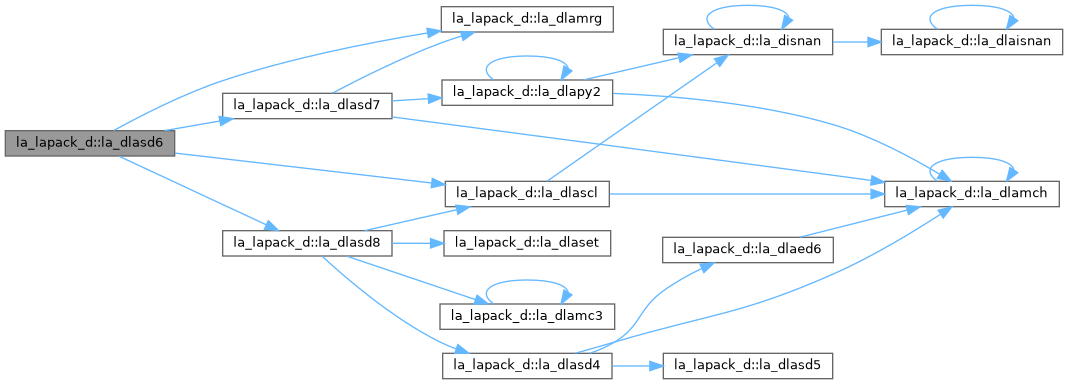
la_dlasd7()

pure subroutine, public la_lapack_d::la_dlasd7	(	integer(ilp), intent(in)	icompq,
		integer(ilp), intent(in)	nl,
		integer(ilp), intent(in)	nr,
		integer(ilp), intent(in)	sqre,
		integer(ilp), intent(out)	k,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(out)	z,
		real(dp), dimension(*), intent(out)	zw,
		real(dp), dimension(*), intent(inout)	vf,
		real(dp), dimension(*), intent(out)	vfw,
		real(dp), dimension(*), intent(inout)	vl,
		real(dp), dimension(*), intent(out)	vlw,
		real(dp), intent(in)	alpha,
		real(dp), intent(in)	beta,
		real(dp), dimension(*), intent(out)	dsigma,
		integer(ilp), dimension(*), intent(out)	idx,
		integer(ilp), dimension(*), intent(out)	idxp,
		integer(ilp), dimension(*), intent(inout)	idxq,
		integer(ilp), dimension(*), intent(out)	perm,
		integer(ilp), intent(out)	givptr,
		integer(ilp), dimension(ldgcol,*), intent(out)	givcol,
		integer(ilp), intent(in)	ldgcol,
		real(dp), dimension(ldgnum,*), intent(out)	givnum,
		integer(ilp), intent(in)	ldgnum,
		real(dp), intent(out)	c,
		real(dp), intent(out)	s,
		integer(ilp), intent(out)	info
	)

DLASD7: merges the two sets of singular values together into a single sorted set. Then it tries to deflate the size of the problem. There are two ways in which deflation can occur: when two or more singular values are close together or if there is a tiny entry in the Z vector. For each such occurrence the order of the related secular equation problem is reduced by one. DLASD7 is called from DLASD6.

Here is the call graph for this function:

la_dlasd8()

pure subroutine, public la_lapack_d::la_dlasd8	(	integer(ilp), intent(in)	icompq,
		integer(ilp), intent(in)	k,
		real(dp), dimension(*), intent(out)	d,
		real(dp), dimension(*), intent(inout)	z,
		real(dp), dimension(*), intent(inout)	vf,
		real(dp), dimension(*), intent(inout)	vl,
		real(dp), dimension(*), intent(out)	difl,
		real(dp), dimension(lddifr,*), intent(out)	difr,
		integer(ilp), intent(in)	lddifr,
		real(dp), dimension(*), intent(inout)	dsigma,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DLASD8: finds the square roots of the roots of the secular equation, as defined by the values in DSIGMA and Z. It makes the appropriate calls to DLASD4, and stores, for each element in D, the distance to its two nearest poles (elements in DSIGMA). It also updates the arrays VF and VL, the first and last components of all the right singular vectors of the original bidiagonal matrix. DLASD8 is called from DLASD6.

Here is the call graph for this function:

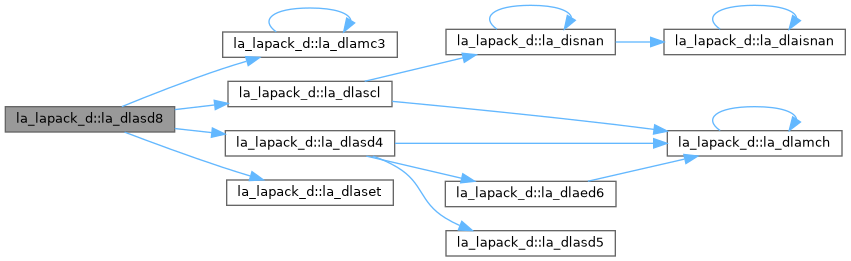
la_dlasda()

pure subroutine, public la_lapack_d::la_dlasda	(	integer(ilp), intent(in)	icompq,
		integer(ilp), intent(in)	smlsiz,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	sqre,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(inout)	e,
		real(dp), dimension(ldu,*), intent(out)	u,
		integer(ilp), intent(in)	ldu,
		real(dp), dimension(ldu,*), intent(out)	vt,
		integer(ilp), dimension(*), intent(out)	k,
		real(dp), dimension(ldu,*), intent(out)	difl,
		real(dp), dimension(ldu,*), intent(out)	difr,
		real(dp), dimension(ldu,*), intent(out)	z,
		real(dp), dimension(ldu,*), intent(out)	poles,
		integer(ilp), dimension(*), intent(out)	givptr,
		integer(ilp), dimension(ldgcol,*), intent(out)	givcol,
		integer(ilp), intent(in)	ldgcol,
		integer(ilp), dimension(ldgcol, *), intent(out)	perm,
		real(dp), dimension(ldu,*), intent(out)	givnum,
		real(dp), dimension(*), intent(out)	c,
		real(dp), dimension(*), intent(out)	s,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

Using a divide and conquer approach, DLASDA: computes the singular value decomposition (SVD) of a real upper bidiagonal N-by-M matrix B with diagonal D and offdiagonal E, where M = N + SQRE. The algorithm computes the singular values in the SVD B = U * S * VT. The orthogonal matrices U and VT are optionally computed in compact form. A related subroutine, DLASD0, computes the singular values and the singular vectors in explicit form.

Here is the call graph for this function:

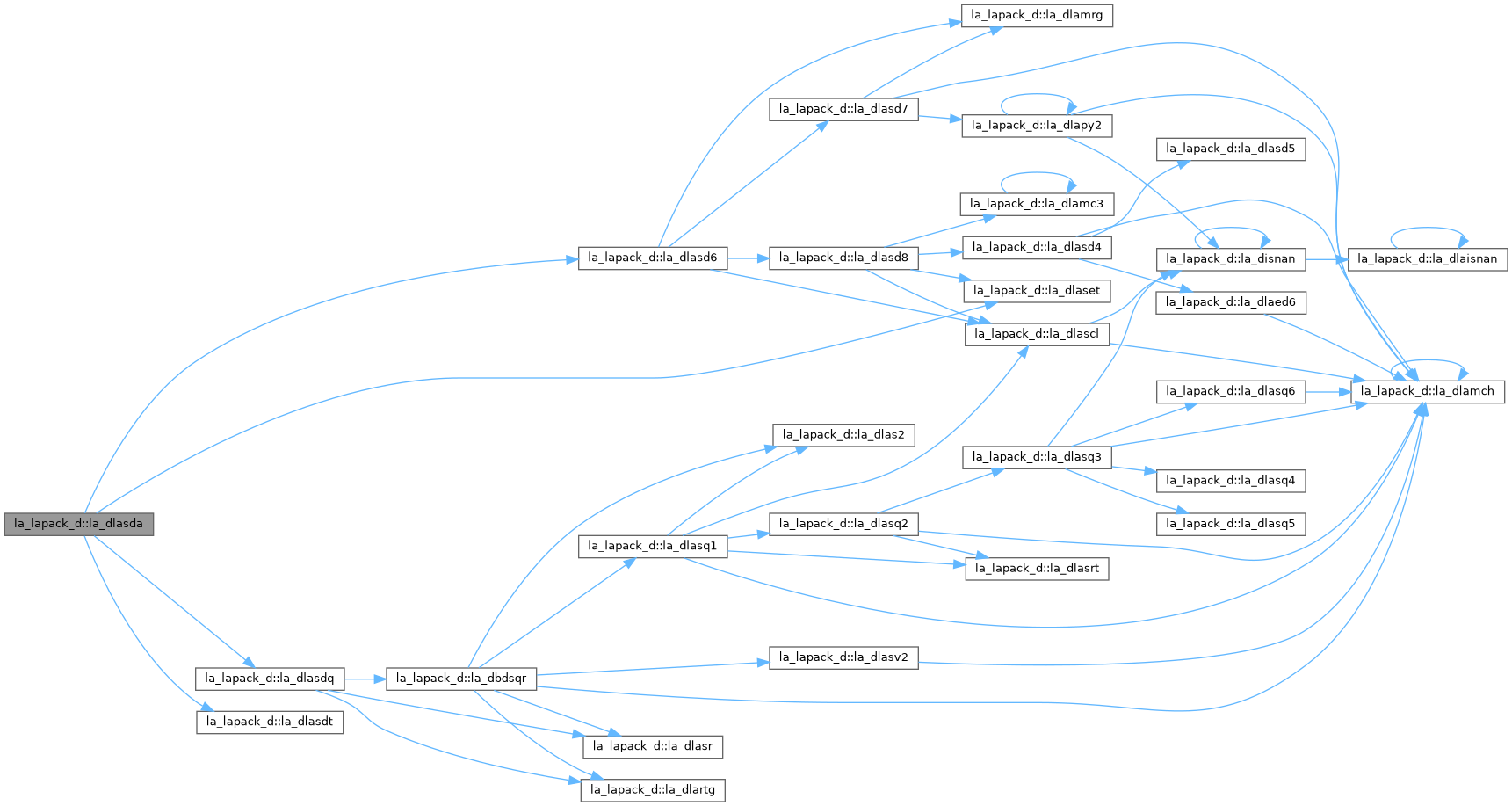
la_dlasdq()

pure subroutine, public la_lapack_d::la_dlasdq	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	sqre,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ncvt,
		integer(ilp), intent(in)	nru,
		integer(ilp), intent(in)	ncc,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(inout)	e,
		real(dp), dimension(ldvt,*), intent(inout)	vt,
		integer(ilp), intent(in)	ldvt,
		real(dp), dimension(ldu,*), intent(inout)	u,
		integer(ilp), intent(in)	ldu,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DLASDQ: computes the singular value decomposition (SVD) of a real (upper or lower) bidiagonal matrix with diagonal D and offdiagonal E, accumulating the transformations if desired. Letting B denote the input bidiagonal matrix, the algorithm computes orthogonal matrices Q and P such that B = Q * S * P**T (P**T denotes the transpose of P). The singular values S are overwritten on D. The input matrix U is changed to U * Q if desired. The input matrix VT is changed to P**T * VT if desired. The input matrix C is changed to Q**T * C if desired. See "Computing Small Singular Values of Bidiagonal Matrices With Guaranteed High Relative Accuracy," by J. Demmel and W. Kahan, LAPACK Working Note #3, for a detailed description of the algorithm.

Here is the call graph for this function:

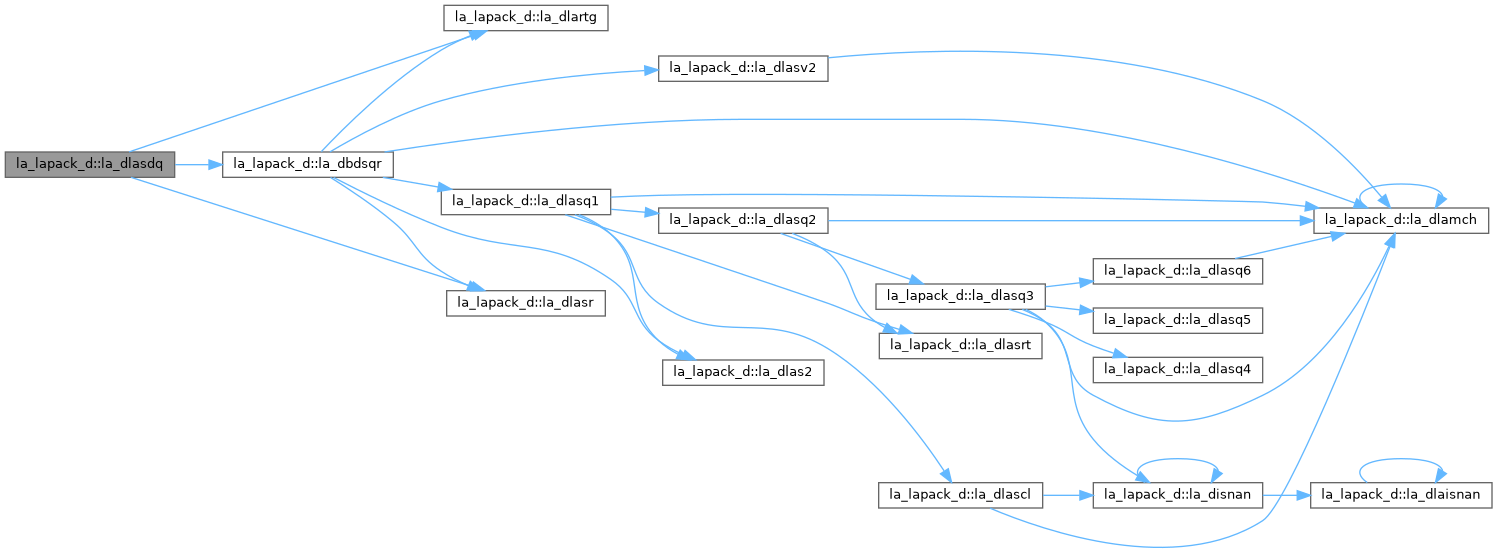
la_dlasdt()

pure subroutine, public la_lapack_d::la_dlasdt	(	integer(ilp), intent(in)	n,
		integer(ilp), intent(out)	lvl,
		integer(ilp), intent(out)	nd,
		integer(ilp), dimension(*), intent(out)	inode,
		integer(ilp), dimension(*), intent(out)	ndiml,
		integer(ilp), dimension(*), intent(out)	ndimr,
		integer(ilp), intent(in)	msub
	)

DLASDT: creates a tree of subproblems for bidiagonal divide and conquer.

la_dlaset()

pure subroutine, public la_lapack_d::la_dlaset	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), intent(in)	alpha,
		real(dp), intent(in)	beta,
		real(dp), dimension(lda,*), intent(out)	a,
		integer(ilp), intent(in)	lda
	)

DLASET: initializes an m-by-n matrix A to BETA on the diagonal and ALPHA on the offdiagonals.

la_dlasq1()

pure subroutine, public la_lapack_d::la_dlasq1	(	integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(inout)	e,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DLASQ1: computes the singular values of a real N-by-N bidiagonal matrix with diagonal D and off-diagonal E. The singular values are computed to high relative accuracy, in the absence of denormalization, underflow and overflow. The algorithm was first presented in "Accurate singular values and differential qd algorithms" by K. V. Fernando and B. N. Parlett, Numer. Math., Vol-67, No. 2, pp. 191-230, 1994, and the present implementation is described in "An implementation of the dqds Algorithm (Positive Case)", LAPACK Working Note.

Here is the call graph for this function:

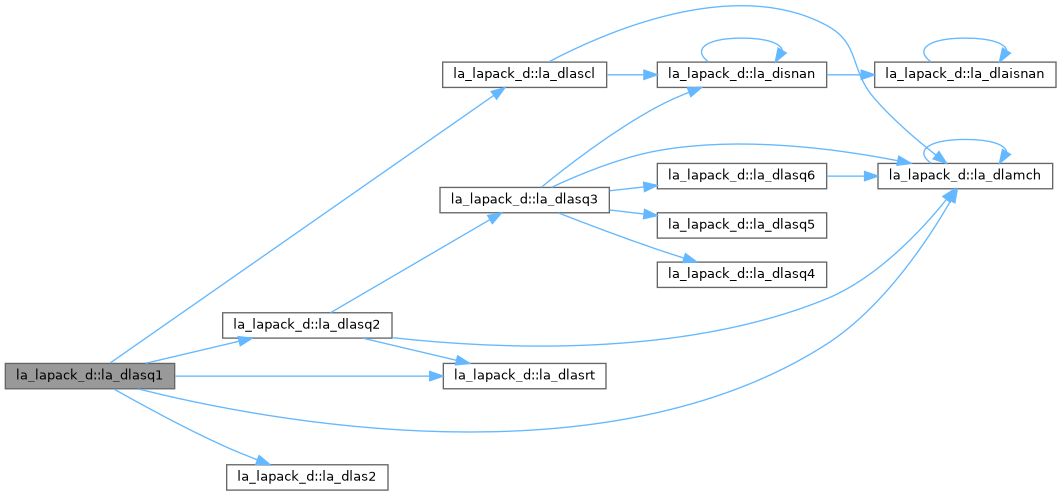
la_dlasq2()

pure subroutine, public la_lapack_d::la_dlasq2	(	integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	z,
		integer(ilp), intent(out)	info
	)

DLASQ2: computes all the eigenvalues of the symmetric positive definite tridiagonal matrix associated with the qd array Z to high relative accuracy are computed to high relative accuracy, in the absence of denormalization, underflow and overflow. To see the relation of Z to the tridiagonal matrix, let L be a unit lower bidiagonal matrix with subdiagonals Z(2,4,6,,..) and let U be an upper bidiagonal matrix with 1's above and diagonal Z(1,3,5,,..). The tridiagonal is L*U or, if you prefer, the symmetric tridiagonal to which it is similar. Note : DLASQ2 defines a logical variable, IEEE, which is true on machines which follow ieee-754 floating-point standard in their handling of infinities and NaNs, and false otherwise. This variable is passed to DLASQ3.

Here is the call graph for this function:

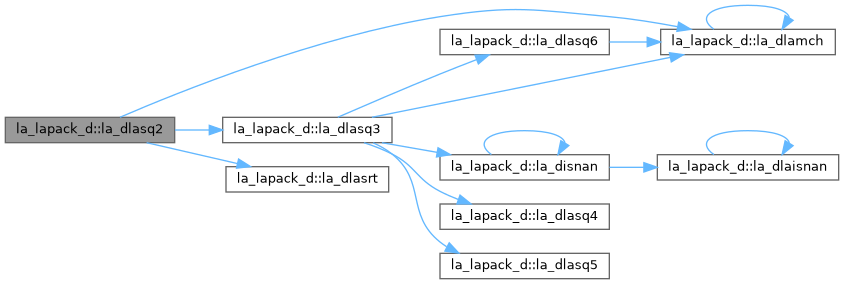
la_dlasq3()

pure subroutine, public la_lapack_d::la_dlasq3	(	integer(ilp), intent(in)	i0,
		integer(ilp), intent(inout)	n0,
		real(dp), dimension(*), intent(inout)	z,
		integer(ilp), intent(inout)	pp,
		real(dp), intent(out)	dmin,
		real(dp), intent(out)	sigma,
		real(dp), intent(inout)	desig,
		real(dp), intent(inout)	qmax,
		integer(ilp), intent(inout)	nfail,
		integer(ilp), intent(inout)	iter,
		integer(ilp), intent(inout)	ndiv,
		logical(lk), intent(in)	ieee,
		integer(ilp), intent(inout)	ttype,
		real(dp), intent(inout)	dmin1,
		real(dp), intent(inout)	dmin2,
		real(dp), intent(inout)	dn,
		real(dp), intent(inout)	dn1,
		real(dp), intent(inout)	dn2,
		real(dp), intent(inout)	g,
		real(dp), intent(inout)	tau
	)

DLASQ3: checks for deflation, computes a shift (TAU) and calls dqds. In case of failure it changes shifts, and tries again until output is positive.

Here is the call graph for this function:

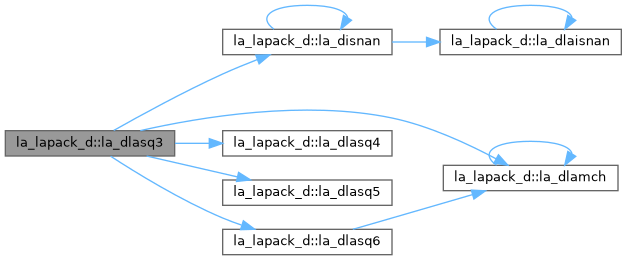
la_dlasq4()

pure subroutine, public la_lapack_d::la_dlasq4	(	integer(ilp), intent(in)	i0,
		integer(ilp), intent(in)	n0,
		real(dp), dimension(*), intent(in)	z,
		integer(ilp), intent(in)	pp,
		integer(ilp), intent(in)	n0in,
		real(dp), intent(in)	dmin,
		real(dp), intent(in)	dmin1,
		real(dp), intent(in)	dmin2,
		real(dp), intent(in)	dn,
		real(dp), intent(in)	dn1,
		real(dp), intent(in)	dn2,
		real(dp), intent(out)	tau,
		integer(ilp), intent(out)	ttype,
		real(dp), intent(inout)	g
	)

DLASQ4: computes an approximation TAU to the smallest eigenvalue using values of d from the previous transform.

la_dlasq5()

pure subroutine, public la_lapack_d::la_dlasq5	(	integer(ilp), intent(in)	i0,
		integer(ilp), intent(in)	n0,
		real(dp), dimension(*), intent(inout)	z,
		integer(ilp), intent(in)	pp,
		real(dp), intent(inout)	tau,
		real(dp), intent(in)	sigma,
		real(dp), intent(out)	dmin,
		real(dp), intent(out)	dmin1,
		real(dp), intent(out)	dmin2,
		real(dp), intent(out)	dn,
		real(dp), intent(out)	dnm1,
		real(dp), intent(out)	dnm2,
		logical(lk), intent(in)	ieee,
		real(dp), intent(in)	eps
	)

DLASQ5: computes one dqds transform in ping-pong form, one version for IEEE machines another for non IEEE machines.

la_dlasq6()

pure subroutine, public la_lapack_d::la_dlasq6	(	integer(ilp), intent(in)	i0,
		integer(ilp), intent(in)	n0,
		real(dp), dimension(*), intent(inout)	z,
		integer(ilp), intent(in)	pp,
		real(dp), intent(out)	dmin,
		real(dp), intent(out)	dmin1,
		real(dp), intent(out)	dmin2,
		real(dp), intent(out)	dn,
		real(dp), intent(out)	dnm1,
		real(dp), intent(out)	dnm2
	)

DLASQ6: computes one dqd (shift equal to zero) transform in ping-pong form, with protection against underflow and overflow.

Here is the call graph for this function:

la_dlasr()

pure subroutine, public la_lapack_d::la_dlasr	(	character, intent(in)	side,
		character, intent(in)	pivot,
		character, intent(in)	direct,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(in)	c,
		real(dp), dimension(*), intent(in)	s,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda
	)

DLASR: applies a sequence of plane rotations to a real matrix A, from either the left or the right. When SIDE = 'L', the transformation takes the form A := P*A and when SIDE = 'R', the transformation takes the form A := A*P**T where P is an orthogonal matrix consisting of a sequence of z plane rotations, with z = M when SIDE = 'L' and z = N when SIDE = 'R', and P**T is the transpose of P. When DIRECT = 'F' (Forward sequence), then P = P(z-1) * ... * P(2) * P(1) and when DIRECT = 'B' (Backward sequence), then P = P(1) * P(2) * ... * P(z-1) where P(k) is a plane rotation matrix defined by the 2-by-2 rotation R(k) = ( c(k) s(k) ) = ( -s(k) c(k) ). When PIVOT = 'V' (Variable pivot), the rotation is performed for the plane (k,k+1), i.e., P(k) has the form P(k) = ( 1 ) ( ... ) ( 1 ) ( c(k) s(k) ) ( -s(k) c(k) ) ( 1 ) ( ... ) ( 1 ) where R(k) appears as a rank-2 modification to the identity matrix in rows and columns k and k+1. When PIVOT = 'T' (Top pivot), the rotation is performed for the plane (1,k+1), so P(k) has the form P(k) = ( c(k) s(k) ) ( 1 ) ( ... ) ( 1 ) ( -s(k) c(k) ) ( 1 ) ( ... ) ( 1 ) where R(k) appears in rows and columns 1 and k+1. Similarly, when PIVOT = 'B' (Bottom pivot), the rotation is performed for the plane (k,z), giving P(k) the form P(k) = ( 1 ) ( ... ) ( 1 ) ( c(k) s(k) ) ( 1 ) ( ... ) ( 1 ) ( -s(k) c(k) ) where R(k) appears in rows and columns k and z. The rotations are performed without ever forming P(k) explicitly.

la_dlasrt()

pure subroutine, public la_lapack_d::la_dlasrt	(	character, intent(in)	id,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	d,
		integer(ilp), intent(out)	info
	)

Sort the numbers in D in increasing order (if ID = 'I') or in decreasing order (if ID = 'D' ). Use Quick Sort, reverting to Insertion sort on arrays of size <= 20. Dimension of STACK limits N to about 2**32.

la_dlassq()

pure subroutine, public la_lapack_d::la_dlassq	(	integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(in)	x,
		integer(ilp), intent(in)	incx,
		real(dp), intent(inout)	scl,
		real(dp), intent(inout)	sumsq
	)

!

DLASSQ: returns the values scl and smsq such that ( scl**2 )*smsq = x( 1 )**2 +...+ x( n )**2 + ( scale**2 )*sumsq, where x( i ) = X( 1 + ( i - 1 )*INCX ). The value of sumsq is assumed to be non-negative. scale and sumsq must be supplied in SCALE and SUMSQ and scl and smsq are overwritten on SCALE and SUMSQ respectively. If scale * sqrt( sumsq ) > tbig then we require: scale >= sqrt( TINY*EPS ) / sbig on entry, and if 0 < scale * sqrt( sumsq ) < tsml then we require: scale <= sqrt( HUGE ) / ssml on entry, where tbig – upper threshold for values whose square is representable; sbig – scaling constant for big numbers;

See also

la_constants.f90 tsml – lower threshold for values whose square is representable; ssml – scaling constant for small numbers;

la_constants.f90 and TINY*EPS – tiniest representable number; HUGE – biggest representable number.

la_dlasv2()

pure subroutine, public la_lapack_d::la_dlasv2	(	real(dp), intent(in)	f,
		real(dp), intent(in)	g,
		real(dp), intent(in)	h,
		real(dp), intent(out)	ssmin,
		real(dp), intent(out)	ssmax,
		real(dp), intent(out)	snr,
		real(dp), intent(out)	csr,
		real(dp), intent(out)	snl,
		real(dp), intent(out)	csl
	)

DLASV2: computes the singular value decomposition of a 2-by-2 triangular matrix [ F G ] [ 0 H ]. On return, abs(SSMAX) is the larger singular value, abs(SSMIN) is the smaller singular value, and (CSL,SNL) and (CSR,SNR) are the left and right singular vectors for abs(SSMAX), giving the decomposition [ CSL SNL ] [ F G ] [ CSR -SNR ] = [ SSMAX 0 ] [-SNL CSL ] [ 0 H ] [ SNR CSR ] [ 0 SSMIN ].

Here is the call graph for this function:

la_dlaswlq()

pure subroutine, public la_lapack_d::la_dlaswlq	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	mb,
		integer(ilp), intent(in)	nb,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldt,*), intent(out)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DLASWLQ: computes a blocked Tall-Skinny LQ factorization of a real M-by-N matrix A for M <= N: A = ( L 0 ) * Q, where: Q is a n-by-N orthogonal matrix, stored on exit in an implicit form in the elements above the diagonal of the array A and in the elements of the array T; L is a lower-triangular M-by-M matrix stored on exit in the elements on and below the diagonal of the array A. 0 is a M-by-(N-M) zero matrix, if M < N, and is not stored.

Here is the call graph for this function:

la_dlaswp()

pure subroutine, public la_lapack_d::la_dlaswp	(	integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), intent(in)	k1,
		integer(ilp), intent(in)	k2,
		integer(ilp), dimension(*), intent(in)	ipiv,
		integer(ilp), intent(in)	incx
	)

DLASWP: performs a series of row interchanges on the matrix A. One row interchange is initiated for each of rows K1 through K2 of A.

la_dlasy2()

pure subroutine, public la_lapack_d::la_dlasy2	(	logical(lk), intent(in)	ltranl,
		logical(lk), intent(in)	ltranr,
		integer(ilp), intent(in)	isgn,
		integer(ilp), intent(in)	n1,
		integer(ilp), intent(in)	n2,
		real(dp), dimension(ldtl,*), intent(in)	tl,
		integer(ilp), intent(in)	ldtl,
		real(dp), dimension(ldtr,*), intent(in)	tr,
		integer(ilp), intent(in)	ldtr,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), intent(out)	scale,
		real(dp), dimension(ldx,*), intent(out)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), intent(out)	xnorm,
		integer(ilp), intent(out)	info
	)

DLASY2: solves for the N1 by N2 matrix X, 1 <= N1,N2 <= 2, in op(TL)*X + ISGN*X*op(TR) = SCALE*B, where TL is N1 by N1, TR is N2 by N2, B is N1 by N2, and ISGN = 1 or -1. op(T) = T or T**T, where T**T denotes the transpose of T.

Here is the call graph for this function:

la_dlasyf()

pure subroutine, public la_lapack_d::la_dlasyf	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nb,
		integer(ilp), intent(out)	kb,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(out)	ipiv,
		real(dp), dimension(ldw,*), intent(out)	w,
		integer(ilp), intent(in)	ldw,
		integer(ilp), intent(out)	info
	)

DLASYF: computes a partial factorization of a real symmetric matrix A using the Bunch-Kaufman diagonal pivoting method. The partial factorization has the form: A = ( I U12 ) ( A11 0 ) ( I 0 ) if UPLO = 'U', or: ( 0 U22 ) ( 0 D ) ( U12**T U22**T ) A = ( L11 0 ) ( D 0 ) ( L11**T L21**T ) if UPLO = 'L' ( L21 I ) ( 0 A22 ) ( 0 I ) where the order of D is at most NB. The actual order is returned in the argument KB, and is either NB or NB-1, or N if N <= NB. DLASYF is an auxiliary routine called by DSYTRF. It uses blocked code (calling Level 3 BLAS) to update the submatrix A11 (if UPLO = 'U') or A22 (if UPLO = 'L').

la_dlasyf_aa()

pure subroutine, public la_lapack_d::la_dlasyf_aa	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	j1,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	nb,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(out)	ipiv,
		real(dp), dimension(ldh,*), intent(inout)	h,
		integer(ilp), intent(in)	ldh,
		real(dp), dimension(*), intent(out)	work
	)

DLATRF_AA factorizes a panel of a real symmetric matrix A using the Aasen's algorithm. The panel consists of a set of NB rows of A when UPLO is U, or a set of NB columns when UPLO is L. In order to factorize the panel, the Aasen's algorithm requires the last row, or column, of the previous panel. The first row, or column, of A is set to be the first row, or column, of an identity matrix, which is used to factorize the first panel. The resulting J-th row of U, or J-th column of L, is stored in the (J-1)-th row, or column, of A (without the unit diagonals), while the diagonal and subdiagonal of A are overwritten by those of T.

Here is the call graph for this function:

la_dlasyf_rk()

pure subroutine, public la_lapack_d::la_dlasyf_rk	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nb,
		integer(ilp), intent(out)	kb,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	e,
		integer(ilp), dimension(*), intent(out)	ipiv,
		real(dp), dimension(ldw,*), intent(out)	w,
		integer(ilp), intent(in)	ldw,
		integer(ilp), intent(out)	info
	)

DLASYF_RK: computes a partial factorization of a real symmetric matrix A using the bounded Bunch-Kaufman (rook) diagonal pivoting method. The partial factorization has the form: A = ( I U12 ) ( A11 0 ) ( I 0 ) if UPLO = 'U', or: ( 0 U22 ) ( 0 D ) ( U12**T U22**T ) A = ( L11 0 ) ( D 0 ) ( L11**T L21**T ) if UPLO = 'L', ( L21 I ) ( 0 A22 ) ( 0 I ) where the order of D is at most NB. The actual order is returned in the argument KB, and is either NB or NB-1, or N if N <= NB. DLASYF_RK is an auxiliary routine called by DSYTRF_RK. It uses blocked code (calling Level 3 BLAS) to update the submatrix A11 (if UPLO = 'U') or A22 (if UPLO = 'L').

Here is the call graph for this function:

la_dlasyf_rook()

pure subroutine, public la_lapack_d::la_dlasyf_rook	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nb,
		integer(ilp), intent(out)	kb,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(out)	ipiv,
		real(dp), dimension(ldw,*), intent(out)	w,
		integer(ilp), intent(in)	ldw,
		integer(ilp), intent(out)	info
	)

DLASYF_ROOK: computes a partial factorization of a real symmetric matrix A using the bounded Bunch-Kaufman ("rook") diagonal pivoting method. The partial factorization has the form: A = ( I U12 ) ( A11 0 ) ( I 0 ) if UPLO = 'U', or: ( 0 U22 ) ( 0 D ) ( U12**T U22**T ) A = ( L11 0 ) ( D 0 ) ( L11**T L21**T ) if UPLO = 'L' ( L21 I ) ( 0 A22 ) ( 0 I ) where the order of D is at most NB. The actual order is returned in the argument KB, and is either NB or NB-1, or N if N <= NB. DLASYF_ROOK is an auxiliary routine called by DSYTRF_ROOK. It uses blocked code (calling Level 3 BLAS) to update the submatrix A11 (if UPLO = 'U') or A22 (if UPLO = 'L').

Here is the call graph for this function:

la_dlat2s()

pure subroutine, public la_lapack_d::la_dlat2s	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(sp), dimension(ldsa,*), intent(out)	sa,
		integer(ilp), intent(in)	ldsa,
		integer(ilp), intent(out)	info
	)

DLAT2S: converts a DOUBLE PRECISION triangular matrix, SA, to a SINGLE PRECISION triangular matrix, A. RMAX is the overflow for the SINGLE PRECISION arithmetic DLAS2S checks that all the entries of A are between -RMAX and RMAX. If not the conversion is aborted and a flag is raised. This is an auxiliary routine so there is no argument checking.

Here is the call graph for this function:

la_dlatbs()

pure subroutine, public la_lapack_d::la_dlatbs	(	character, intent(in)	uplo,
		character, intent(in)	trans,
		character, intent(in)	diag,
		character, intent(in)	normin,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kd,
		real(dp), dimension(ldab,*), intent(in)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(*), intent(inout)	x,
		real(dp), intent(out)	scale,
		real(dp), dimension(*), intent(inout)	cnorm,
		integer(ilp), intent(out)	info
	)

DLATBS: solves one of the triangular systems A *x = s*b or A**T*x = s*b with scaling to prevent overflow, where A is an upper or lower triangular band matrix. Here A**T denotes the transpose of A, x and b are n-element vectors, and s is a scaling factor, usually less than or equal to 1, chosen so that the components of x will be less than the overflow threshold. If the unscaled problem will not cause overflow, the Level 2 BLAS routine DTBSV is called. If the matrix A is singular (A(j,j) = 0 for some j), then s is set to 0 and a non-trivial solution to A*x = 0 is returned.

Here is the call graph for this function:

la_dlatdf()

pure subroutine, public la_lapack_d::la_dlatdf	(	integer(ilp), intent(in)	ijob,
		integer(ilp), intent(in)	n,
		real(dp), dimension(ldz,*), intent(inout)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(inout)	rhs,
		real(dp), intent(inout)	rdsum,
		real(dp), intent(inout)	rdscal,
		integer(ilp), dimension(*), intent(in)	ipiv,
		integer(ilp), dimension(*), intent(in)	jpiv
	)

DLATDF: uses the LU factorization of the n-by-n matrix Z computed by DGETC2 and computes a contribution to the reciprocal Dif-estimate by solving Z * x = b for x, and choosing the r.h.s. b such that the norm of x is as large as possible. On entry RHS = b holds the contribution from earlier solved sub-systems, and on return RHS = x. The factorization of Z returned by DGETC2 has the form Z = P*L*U*Q, where P and Q are permutation matrices. L is lower triangular with unit diagonal elements and U is upper triangular.

Here is the call graph for this function:

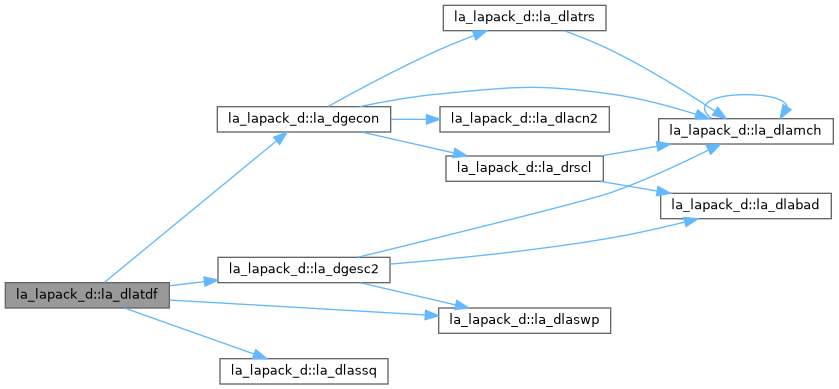
la_dlatps()

pure subroutine, public la_lapack_d::la_dlatps	(	character, intent(in)	uplo,
		character, intent(in)	trans,
		character, intent(in)	diag,
		character, intent(in)	normin,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(in)	ap,
		real(dp), dimension(*), intent(inout)	x,
		real(dp), intent(out)	scale,
		real(dp), dimension(*), intent(inout)	cnorm,
		integer(ilp), intent(out)	info
	)

DLATPS: solves one of the triangular systems A *x = s*b or A**T*x = s*b with scaling to prevent overflow, where A is an upper or lower triangular matrix stored in packed form. Here A**T denotes the transpose of A, x and b are n-element vectors, and s is a scaling factor, usually less than or equal to 1, chosen so that the components of x will be less than the overflow threshold. If the unscaled problem will not cause overflow, the Level 2 BLAS routine DTPSV is called. If the matrix A is singular (A(j,j) = 0 for some j), then s is set to 0 and a non-trivial solution to A*x = 0 is returned.

Here is the call graph for this function:

la_dlatrd()

pure subroutine, public la_lapack_d::la_dlatrd	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nb,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	e,
		real(dp), dimension(*), intent(out)	tau,
		real(dp), dimension(ldw,*), intent(out)	w,
		integer(ilp), intent(in)	ldw
	)

DLATRD: reduces NB rows and columns of a real symmetric matrix A to symmetric tridiagonal form by an orthogonal similarity transformation Q**T * A * Q, and returns the matrices V and W which are needed to apply the transformation to the unreduced part of A. If UPLO = 'U', DLATRD reduces the last NB rows and columns of a matrix, of which the upper triangle is supplied; if UPLO = 'L', DLATRD reduces the first NB rows and columns of a matrix, of which the lower triangle is supplied. This is an auxiliary routine called by DSYTRD.

Here is the call graph for this function:

la_dlatrs()

pure subroutine, public la_lapack_d::la_dlatrs	(	character, intent(in)	uplo,
		character, intent(in)	trans,
		character, intent(in)	diag,
		character, intent(in)	normin,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(inout)	x,
		real(dp), intent(out)	scale,
		real(dp), dimension(*), intent(inout)	cnorm,
		integer(ilp), intent(out)	info
	)

DLATRS: solves one of the triangular systems A *x = s*b or A**T *x = s*b with scaling to prevent overflow. Here A is an upper or lower triangular matrix, A**T denotes the transpose of A, x and b are n-element vectors, and s is a scaling factor, usually less than or equal to 1, chosen so that the components of x will be less than the overflow threshold. If the unscaled problem will not cause overflow, the Level 2 BLAS routine DTRSV is called. If the matrix A is singular (A(j,j) = 0 for some j), then s is set to 0 and a non-trivial solution to A*x = 0 is returned.

Here is the call graph for this function:

la_dlatrz()

pure subroutine, public la_lapack_d::la_dlatrz	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	l,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	tau,
		real(dp), dimension(*), intent(out)	work
	)

DLATRZ: factors the M-by-(M+L) real upper trapezoidal matrix [ A1 A2 ] = [ A(1:M,1:M) A(1:M,N-L+1:N) ] as ( R 0 ) * Z, by means of orthogonal transformations. Z is an (M+L)-by-(M+L) orthogonal matrix and, R and A1 are M-by-M upper triangular matrices.

Here is the call graph for this function:

la_dlatsqr()

pure subroutine, public la_lapack_d::la_dlatsqr	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	mb,
		integer(ilp), intent(in)	nb,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldt,*), intent(out)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DLATSQR: computes a blocked Tall-Skinny QR factorization of a real M-by-N matrix A for M >= N: A = Q * ( R ), ( 0 ) where: Q is a M-by-M orthogonal matrix, stored on exit in an implicit form in the elements below the diagonal of the array A and in the elements of the array T; R is an upper-triangular N-by-N matrix, stored on exit in the elements on and above the diagonal of the array A. 0 is a (M-N)-by-N zero matrix, and is not stored.

Here is the call graph for this function:

la_dlauu2()

pure subroutine, public la_lapack_d::la_dlauu2	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), intent(out)	info
	)

DLAUU2: computes the product U * U**T or L**T * L, where the triangular factor U or L is stored in the upper or lower triangular part of the array A. If UPLO = 'U' or 'u' then the upper triangle of the result is stored, overwriting the factor U in A. If UPLO = 'L' or 'l' then the lower triangle of the result is stored, overwriting the factor L in A. This is the unblocked form of the algorithm, calling Level 2 BLAS.

la_dlauum()

pure subroutine, public la_lapack_d::la_dlauum	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), intent(out)	info
	)

DLAUUM: computes the product U * U**T or L**T * L, where the triangular factor U or L is stored in the upper or lower triangular part of the array A. If UPLO = 'U' or 'u' then the upper triangle of the result is stored, overwriting the factor U in A. If UPLO = 'L' or 'l' then the lower triangle of the result is stored, overwriting the factor L in A. This is the blocked form of the algorithm, calling Level 3 BLAS.

Here is the call graph for this function:

la_dopgtr()

pure subroutine, public la_lapack_d::la_dopgtr	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(in)	ap,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(ldq,*), intent(out)	q,
		integer(ilp), intent(in)	ldq,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DOPGTR: generates a real orthogonal matrix Q which is defined as the product of n-1 elementary reflectors H(i) of order n, as returned by DSPTRD using packed storage: if UPLO = 'U', Q = H(n-1) . . . H(2) H(1), if UPLO = 'L', Q = H(1) H(2) . . . H(n-1).

Here is the call graph for this function:

la_dopmtr()

pure subroutine, public la_lapack_d::la_dopmtr	(	character, intent(in)	side,
		character, intent(in)	uplo,
		character, intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	ap,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DOPMTR: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q * C C * Q TRANS = 'T': Q**T * C C * Q**T where Q is a real orthogonal matrix of order nq, with nq = m if SIDE = 'L' and nq = n if SIDE = 'R'. Q is defined as the product of nq-1 elementary reflectors, as returned by DSPTRD using packed storage: if UPLO = 'U', Q = H(nq-1) . . . H(2) H(1); if UPLO = 'L', Q = H(1) H(2) . . . H(nq-1).

Here is the call graph for this function:

la_dorbdb()

subroutine, public la_lapack_d::la_dorbdb	(	character, intent(in)	trans,
		character, intent(in)	signs,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	p,
		integer(ilp), intent(in)	q,
		real(dp), dimension(ldx11,*), intent(inout)	x11,
		integer(ilp), intent(in)	ldx11,
		real(dp), dimension(ldx12,*), intent(inout)	x12,
		integer(ilp), intent(in)	ldx12,
		real(dp), dimension(ldx21,*), intent(inout)	x21,
		integer(ilp), intent(in)	ldx21,
		real(dp), dimension(ldx22,*), intent(inout)	x22,
		integer(ilp), intent(in)	ldx22,
		real(dp), dimension(*), intent(out)	theta,
		real(dp), dimension(*), intent(out)	phi,
		real(dp), dimension(*), intent(out)	taup1,
		real(dp), dimension(*), intent(out)	taup2,
		real(dp), dimension(*), intent(out)	tauq1,
		real(dp), dimension(*), intent(out)	tauq2,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DORBDB: simultaneously bidiagonalizes the blocks of an M-by-M partitioned orthogonal matrix X: [ B11 | B12 0 0 ] [ X11 | X12 ] [ P1 | ] [ 0 | 0 -I 0 ] [ Q1 | ]**T X = [--------—] = [------—] [-------------—] [------—] . [ X21 | X22 ] [ | P2 ] [ B21 | B22 0 0 ] [ | Q2 ] [ 0 | 0 0 I ] X11 is P-by-Q. Q must be no larger than P, M-P, or M-Q. (If this is not the case, then X must be transposed and/or permuted. This can be done in constant time using the TRANS and SIGNS options. See DORCSD for details.) The orthogonal matrices P1, P2, Q1, and Q2 are P-by-P, (M-P)-by- (M-P), Q-by-Q, and (M-Q)-by-(M-Q), respectively. They are represented implicitly by Householder vectors. B11, B12, B21, and B22 are Q-by-Q bidiagonal matrices represented implicitly by angles THETA, PHI.

Here is the call graph for this function:

la_dorbdb1()

subroutine, public la_lapack_d::la_dorbdb1	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	p,
		integer(ilp), intent(in)	q,
		real(dp), dimension(ldx11,*), intent(inout)	x11,
		integer(ilp), intent(in)	ldx11,
		real(dp), dimension(ldx21,*), intent(inout)	x21,
		integer(ilp), intent(in)	ldx21,
		real(dp), dimension(*), intent(out)	theta,
		real(dp), dimension(*), intent(out)	phi,
		real(dp), dimension(*), intent(out)	taup1,
		real(dp), dimension(*), intent(out)	taup2,
		real(dp), dimension(*), intent(out)	tauq1,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DORBDB1: simultaneously bidiagonalizes the blocks of a tall and skinny matrix X with orthonomal columns: [ B11 ] [ X11 ] [ P1 | ] [ 0 ] [--—] = [------—] [--—] Q1**T . [ X21 ] [ | P2 ] [ B21 ] [ 0 ] X11 is P-by-Q, and X21 is (M-P)-by-Q. Q must be no larger than P, M-P, or M-Q. Routines DORBDB2, DORBDB3, and DORBDB4 handle cases in which Q is not the minimum dimension. The orthogonal matrices P1, P2, and Q1 are P-by-P, (M-P)-by-(M-P), and (M-Q)-by-(M-Q), respectively. They are represented implicitly by Householder vectors. B11 and B12 are Q-by-Q bidiagonal matrices represented implicitly by angles THETA, PHI.

Here is the call graph for this function:

la_dorbdb2()

subroutine, public la_lapack_d::la_dorbdb2	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	p,
		integer(ilp), intent(in)	q,
		real(dp), dimension(ldx11,*), intent(inout)	x11,
		integer(ilp), intent(in)	ldx11,
		real(dp), dimension(ldx21,*), intent(inout)	x21,
		integer(ilp), intent(in)	ldx21,
		real(dp), dimension(*), intent(out)	theta,
		real(dp), dimension(*), intent(out)	phi,
		real(dp), dimension(*), intent(out)	taup1,
		real(dp), dimension(*), intent(out)	taup2,
		real(dp), dimension(*), intent(out)	tauq1,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DORBDB2: simultaneously bidiagonalizes the blocks of a tall and skinny matrix X with orthonomal columns: [ B11 ] [ X11 ] [ P1 | ] [ 0 ] [--—] = [------—] [--—] Q1**T . [ X21 ] [ | P2 ] [ B21 ] [ 0 ] X11 is P-by-Q, and X21 is (M-P)-by-Q. P must be no larger than M-P, Q, or M-Q. Routines DORBDB1, DORBDB3, and DORBDB4 handle cases in which P is not the minimum dimension. The orthogonal matrices P1, P2, and Q1 are P-by-P, (M-P)-by-(M-P), and (M-Q)-by-(M-Q), respectively. They are represented implicitly by Householder vectors. B11 and B12 are P-by-P bidiagonal matrices represented implicitly by angles THETA, PHI.

Here is the call graph for this function:

la_dorbdb3()

subroutine, public la_lapack_d::la_dorbdb3	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	p,
		integer(ilp), intent(in)	q,
		real(dp), dimension(ldx11,*), intent(inout)	x11,
		integer(ilp), intent(in)	ldx11,
		real(dp), dimension(ldx21,*), intent(inout)	x21,
		integer(ilp), intent(in)	ldx21,
		real(dp), dimension(*), intent(out)	theta,
		real(dp), dimension(*), intent(out)	phi,
		real(dp), dimension(*), intent(out)	taup1,
		real(dp), dimension(*), intent(out)	taup2,
		real(dp), dimension(*), intent(out)	tauq1,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DORBDB3: simultaneously bidiagonalizes the blocks of a tall and skinny matrix X with orthonomal columns: [ B11 ] [ X11 ] [ P1 | ] [ 0 ] [--—] = [------—] [--—] Q1**T . [ X21 ] [ | P2 ] [ B21 ] [ 0 ] X11 is P-by-Q, and X21 is (M-P)-by-Q. M-P must be no larger than P, Q, or M-Q. Routines DORBDB1, DORBDB2, and DORBDB4 handle cases in which M-P is not the minimum dimension. The orthogonal matrices P1, P2, and Q1 are P-by-P, (M-P)-by-(M-P), and (M-Q)-by-(M-Q), respectively. They are represented implicitly by Householder vectors. B11 and B12 are (M-P)-by-(M-P) bidiagonal matrices represented implicitly by angles THETA, PHI.

Here is the call graph for this function:

la_dorbdb4()

subroutine, public la_lapack_d::la_dorbdb4	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	p,
		integer(ilp), intent(in)	q,
		real(dp), dimension(ldx11,*), intent(inout)	x11,
		integer(ilp), intent(in)	ldx11,
		real(dp), dimension(ldx21,*), intent(inout)	x21,
		integer(ilp), intent(in)	ldx21,
		real(dp), dimension(*), intent(out)	theta,
		real(dp), dimension(*), intent(out)	phi,
		real(dp), dimension(*), intent(out)	taup1,
		real(dp), dimension(*), intent(out)	taup2,
		real(dp), dimension(*), intent(out)	tauq1,
		real(dp), dimension(*), intent(out)	phantom,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DORBDB4: simultaneously bidiagonalizes the blocks of a tall and skinny matrix X with orthonomal columns: [ B11 ] [ X11 ] [ P1 | ] [ 0 ] [--—] = [------—] [--—] Q1**T . [ X21 ] [ | P2 ] [ B21 ] [ 0 ] X11 is P-by-Q, and X21 is (M-P)-by-Q. M-Q must be no larger than P, M-P, or Q. Routines DORBDB1, DORBDB2, and DORBDB3 handle cases in which M-Q is not the minimum dimension. The orthogonal matrices P1, P2, and Q1 are P-by-P, (M-P)-by-(M-P), and (M-Q)-by-(M-Q), respectively. They are represented implicitly by Householder vectors. B11 and B12 are (M-Q)-by-(M-Q) bidiagonal matrices represented implicitly by angles THETA, PHI.

Here is the call graph for this function:

la_dorbdb5()

pure subroutine, public la_lapack_d::la_dorbdb5	(	integer(ilp), intent(in)	m1,
		integer(ilp), intent(in)	m2,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	x1,
		integer(ilp), intent(in)	incx1,
		real(dp), dimension(*), intent(inout)	x2,
		integer(ilp), intent(in)	incx2,
		real(dp), dimension(ldq1,*), intent(in)	q1,
		integer(ilp), intent(in)	ldq1,
		real(dp), dimension(ldq2,*), intent(in)	q2,
		integer(ilp), intent(in)	ldq2,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DORBDB5: orthogonalizes the column vector X = [ X1 ] [ X2 ] with respect to the columns of Q = [ Q1 ] . [ Q2 ] The columns of Q must be orthonormal. If the projection is zero according to Kahan's "twice is enough" criterion, then some other vector from the orthogonal complement is returned. This vector is chosen in an arbitrary but deterministic way.

Here is the call graph for this function:

la_dorbdb6()

pure subroutine, public la_lapack_d::la_dorbdb6	(	integer(ilp), intent(in)	m1,
		integer(ilp), intent(in)	m2,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	x1,
		integer(ilp), intent(in)	incx1,
		real(dp), dimension(*), intent(inout)	x2,
		integer(ilp), intent(in)	incx2,
		real(dp), dimension(ldq1,*), intent(in)	q1,
		integer(ilp), intent(in)	ldq1,
		real(dp), dimension(ldq2,*), intent(in)	q2,
		integer(ilp), intent(in)	ldq2,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DORBDB6: orthogonalizes the column vector X = [ X1 ] [ X2 ] with respect to the columns of Q = [ Q1 ] . [ Q2 ] The columns of Q must be orthonormal. If the projection is zero according to Kahan's "twice is enough" criterion, then the zero vector is returned.

Here is the call graph for this function:

la_dorcsd()

recursive subroutine, public la_lapack_d::la_dorcsd	(	character, intent(in)	jobu1,
		character, intent(in)	jobu2,
		character, intent(in)	jobv1t,
		character, intent(in)	jobv2t,
		character, intent(in)	trans,
		character, intent(in)	signs,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	p,
		integer(ilp), intent(in)	q,
		real(dp), dimension(ldx11,*), intent(inout)	x11,
		integer(ilp), intent(in)	ldx11,
		real(dp), dimension(ldx12,*), intent(inout)	x12,
		integer(ilp), intent(in)	ldx12,
		real(dp), dimension(ldx21,*), intent(inout)	x21,
		integer(ilp), intent(in)	ldx21,
		real(dp), dimension(ldx22,*), intent(inout)	x22,
		integer(ilp), intent(in)	ldx22,
		real(dp), dimension(*), intent(out)	theta,
		real(dp), dimension(ldu1,*), intent(out)	u1,
		integer(ilp), intent(in)	ldu1,
		real(dp), dimension(ldu2,*), intent(out)	u2,
		integer(ilp), intent(in)	ldu2,
		real(dp), dimension(ldv1t,*), intent(out)	v1t,
		integer(ilp), intent(in)	ldv1t,
		real(dp), dimension(ldv2t,*), intent(out)	v2t,
		integer(ilp), intent(in)	ldv2t,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DORCSD: computes the CS decomposition of an M-by-M partitioned orthogonal matrix X: [ I 0 0 | 0 0 0 ] [ 0 C 0 | 0 -S 0 ] [ X11 | X12 ] [ U1 | ] [ 0 0 0 | 0 0 -I ] [ V1 | ]**T X = [--------—] = [------—] [------------------—] [------—] . [ X21 | X22 ] [ | U2 ] [ 0 0 0 | I 0 0 ] [ | V2 ] [ 0 S 0 | 0 C 0 ] [ 0 0 I | 0 0 0 ] X11 is P-by-Q. The orthogonal matrices U1, U2, V1, and V2 are P-by-P, (M-P)-by-(M-P), Q-by-Q, and (M-Q)-by-(M-Q), respectively. C and S are R-by-R nonnegative diagonal matrices satisfying C^2 + S^2 = I, in which R = MIN(P,M-P,Q,M-Q).

Here is the call graph for this function:

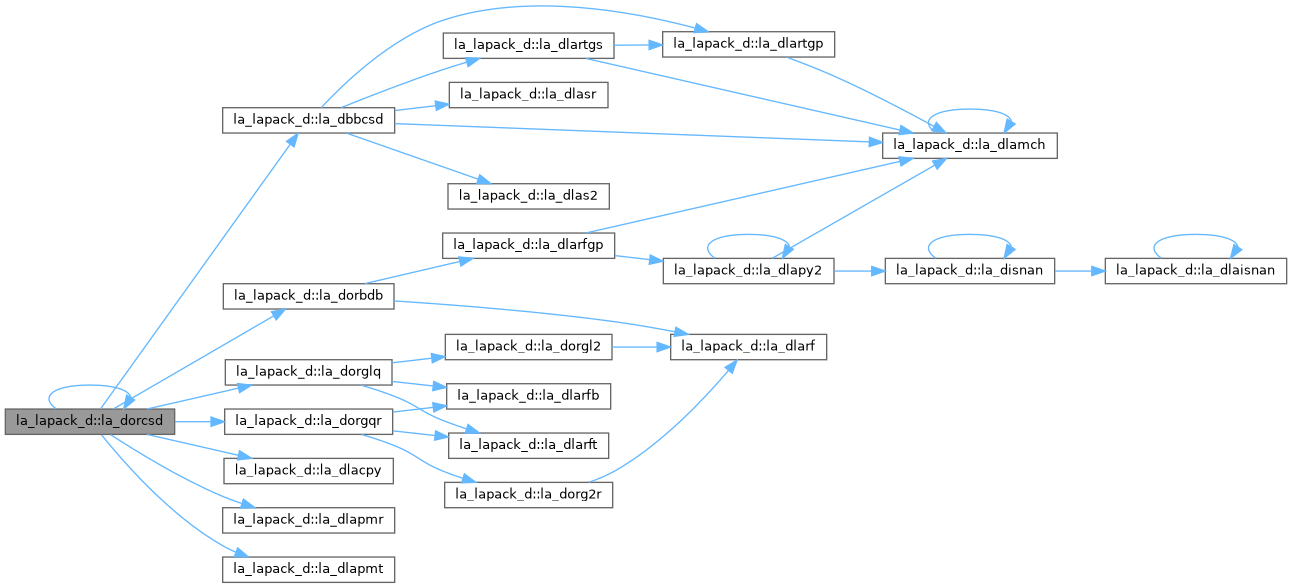
la_dorcsd2by1()

subroutine, public la_lapack_d::la_dorcsd2by1	(	character, intent(in)	jobu1,
		character, intent(in)	jobu2,
		character, intent(in)	jobv1t,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	p,
		integer(ilp), intent(in)	q,
		real(dp), dimension(ldx11,*), intent(inout)	x11,
		integer(ilp), intent(in)	ldx11,
		real(dp), dimension(ldx21,*), intent(inout)	x21,
		integer(ilp), intent(in)	ldx21,
		real(dp), dimension(*), intent(out)	theta,
		real(dp), dimension(ldu1,*), intent(out)	u1,
		integer(ilp), intent(in)	ldu1,
		real(dp), dimension(ldu2,*), intent(out)	u2,
		integer(ilp), intent(in)	ldu2,
		real(dp), dimension(ldv1t,*), intent(out)	v1t,
		integer(ilp), intent(in)	ldv1t,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DORCSD2BY1: computes the CS decomposition of an M-by-Q matrix X with orthonormal columns that has been partitioned into a 2-by-1 block structure: [ I1 0 0 ] [ 0 C 0 ] [ X11 ] [ U1 | ] [ 0 0 0 ] X = [--—] = [------—] [-------—] V1**T . [ X21 ] [ | U2 ] [ 0 0 0 ] [ 0 S 0 ] [ 0 0 I2] X11 is P-by-Q. The orthogonal matrices U1, U2, and V1 are P-by-P, (M-P)-by-(M-P), and Q-by-Q, respectively. C and S are R-by-R nonnegative diagonal matrices satisfying C^2 + S^2 = I, in which R = MIN(P,M-P,Q,M-Q). I1 is a K1-by-K1 identity matrix and I2 is a K2-by-K2 identity matrix, where K1 = MAX(Q+P-M,0), K2 = MAX(Q-P,0).

Here is the call graph for this function:

la_dorg2l()

pure subroutine, public la_lapack_d::la_dorg2l	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DORG2L: generates an m by n real matrix Q with orthonormal columns, which is defined as the last n columns of a product of k elementary reflectors of order m Q = H(k) . . . H(2) H(1) as returned by DGEQLF.

Here is the call graph for this function:

la_dorg2r()

pure subroutine, public la_lapack_d::la_dorg2r	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DORG2R: generates an m by n real matrix Q with orthonormal columns, which is defined as the first n columns of a product of k elementary reflectors of order m Q = H(1) H(2) . . . H(k) as returned by DGEQRF.

Here is the call graph for this function:

la_dorgbr()

pure subroutine, public la_lapack_d::la_dorgbr	(	character, intent(in)	vect,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DORGBR: generates one of the real orthogonal matrices Q or P**T determined by DGEBRD when reducing a real matrix A to bidiagonal form: A = Q * B * P**T. Q and P**T are defined as products of elementary reflectors H(i) or G(i) respectively. If VECT = 'Q', A is assumed to have been an M-by-K matrix, and Q is of order M: if m >= k, Q = H(1) H(2) . . . H(k) and DORGBR returns the first n columns of Q, where m >= n >= k; if m < k, Q = H(1) H(2) . . . H(m-1) and DORGBR returns Q as an M-by-M matrix. If VECT = 'P', A is assumed to have been a K-by-N matrix, and P**T is of order N: if k < n, P**T = G(k) . . . G(2) G(1) and DORGBR returns the first m rows of P**T, where n >= m >= k; if k >= n, P**T = G(n-1) . . . G(2) G(1) and DORGBR returns P**T as an N-by-N matrix.

Here is the call graph for this function:

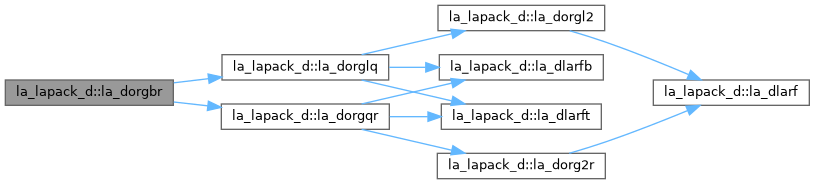
la_dorghr()

pure subroutine, public la_lapack_d::la_dorghr	(	integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ilo,
		integer(ilp), intent(in)	ihi,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DORGHR: generates a real orthogonal matrix Q which is defined as the product of IHI-ILO elementary reflectors of order N, as returned by DGEHRD: Q = H(ilo) H(ilo+1) . . . H(ihi-1).

Here is the call graph for this function:

la_dorgl2()

pure subroutine, public la_lapack_d::la_dorgl2	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DORGL2: generates an m by n real matrix Q with orthonormal rows, which is defined as the first m rows of a product of k elementary reflectors of order n Q = H(k) . . . H(2) H(1) as returned by DGELQF.

Here is the call graph for this function:

la_dorglq()

pure subroutine, public la_lapack_d::la_dorglq	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DORGLQ: generates an M-by-N real matrix Q with orthonormal rows, which is defined as the first M rows of a product of K elementary reflectors of order N Q = H(k) . . . H(2) H(1) as returned by DGELQF.

Here is the call graph for this function:

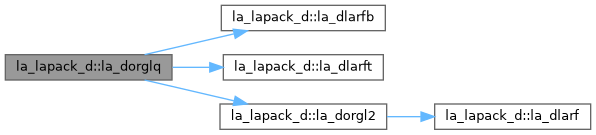
la_dorgql()

pure subroutine, public la_lapack_d::la_dorgql	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DORGQL: generates an M-by-N real matrix Q with orthonormal columns, which is defined as the last N columns of a product of K elementary reflectors of order M Q = H(k) . . . H(2) H(1) as returned by DGEQLF.

Here is the call graph for this function:

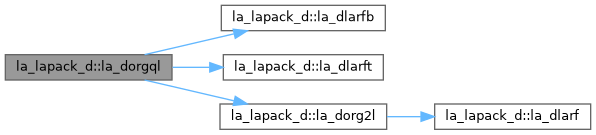
la_dorgqr()

pure subroutine, public la_lapack_d::la_dorgqr	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DORGQR: generates an M-by-N real matrix Q with orthonormal columns, which is defined as the first N columns of a product of K elementary reflectors of order M Q = H(1) H(2) . . . H(k) as returned by DGEQRF.

Here is the call graph for this function:

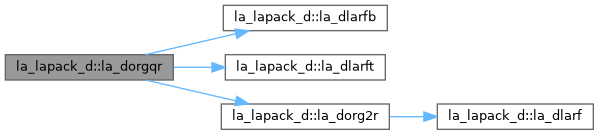
la_dorgr2()

pure subroutine, public la_lapack_d::la_dorgr2	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DORGR2: generates an m by n real matrix Q with orthonormal rows, which is defined as the last m rows of a product of k elementary reflectors of order n Q = H(1) H(2) . . . H(k) as returned by DGERQF.

Here is the call graph for this function:

la_dorgrq()

pure subroutine, public la_lapack_d::la_dorgrq	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DORGRQ: generates an M-by-N real matrix Q with orthonormal rows, which is defined as the last M rows of a product of K elementary reflectors of order N Q = H(1) H(2) . . . H(k) as returned by DGERQF.

Here is the call graph for this function:

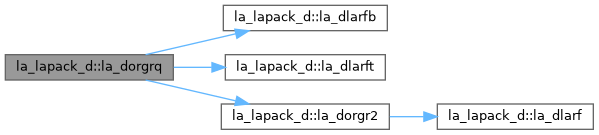
la_dorgtr()

pure subroutine, public la_lapack_d::la_dorgtr	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DORGTR: generates a real orthogonal matrix Q which is defined as the product of n-1 elementary reflectors of order N, as returned by DSYTRD: if UPLO = 'U', Q = H(n-1) . . . H(2) H(1), if UPLO = 'L', Q = H(1) H(2) . . . H(n-1).

Here is the call graph for this function:

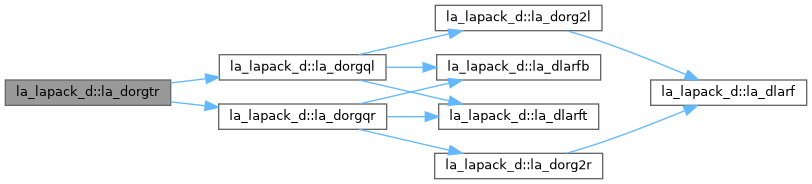
la_dorgtsqr()

pure subroutine, public la_lapack_d::la_dorgtsqr	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	mb,
		integer(ilp), intent(in)	nb,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldt,*), intent(in)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DORGTSQR: generates an M-by-N real matrix Q_out with orthonormal columns, which are the first N columns of a product of real orthogonal matrices of order M which are returned by DLATSQR Q_out = first_N_columns_of( Q(1)_in * Q(2)_in * ... * Q(k)_in ). See the documentation for DLATSQR.

Here is the call graph for this function:

la_dorgtsqr_row()

pure subroutine, public la_lapack_d::la_dorgtsqr_row	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	mb,
		integer(ilp), intent(in)	nb,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldt,*), intent(in)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DORGTSQR_ROW: generates an M-by-N real matrix Q_out with orthonormal columns from the output of DLATSQR. These N orthonormal columns are the first N columns of a product of complex unitary matrices Q(k)_in of order M, which are returned by DLATSQR in a special format. Q_out = first_N_columns_of( Q(1)_in * Q(2)_in * ... * Q(k)_in ). The input matrices Q(k)_in are stored in row and column blocks in A. See the documentation of DLATSQR for more details on the format of Q(k)_in, where each Q(k)_in is represented by block Householder transformations. This routine calls an auxiliary routine DLARFB_GETT, where the computation is performed on each individual block. The algorithm first sweeps NB-sized column blocks from the right to left starting in the bottom row block and continues to the top row block (hence _ROW in the routine name). This sweep is in reverse order of the order in which DLATSQR generates the output blocks.

Here is the call graph for this function:

la_dorhr_col()

pure subroutine, public la_lapack_d::la_dorhr_col	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nb,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldt,*), intent(out)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(*), intent(out)	d,
		integer(ilp), intent(out)	info
	)

DORHR_COL: takes an M-by-N real matrix Q_in with orthonormal columns as input, stored in A, and performs Householder Reconstruction (HR), i.e. reconstructs Householder vectors V(i) implicitly representing another M-by-N matrix Q_out, with the property that Q_in = Q_out*S, where S is an N-by-N diagonal matrix with diagonal entries equal to +1 or -1. The Householder vectors (columns V(i) of V) are stored in A on output, and the diagonal entries of S are stored in D. Block reflectors are also returned in T (same output format as DGEQRT).

Here is the call graph for this function:

la_dorm22()

pure subroutine, public la_lapack_d::la_dorm22	(	character, intent(in)	side,
		character, intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	n1,
		integer(ilp), intent(in)	n2,
		real(dp), dimension(ldq,*), intent(in)	q,
		integer(ilp), intent(in)	ldq,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

Here is the call graph for this function:

la_dorm2l()

pure subroutine, public la_lapack_d::la_dorm2l	(	character, intent(in)	side,
		character, intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DORM2L: overwrites the general real m by n matrix C with Q * C if SIDE = 'L' and TRANS = 'N', or Q**T * C if SIDE = 'L' and TRANS = 'T', or C * Q if SIDE = 'R' and TRANS = 'N', or C * Q**T if SIDE = 'R' and TRANS = 'T', where Q is a real orthogonal matrix defined as the product of k elementary reflectors Q = H(k) . . . H(2) H(1) as returned by DGEQLF. Q is of order m if SIDE = 'L' and of order n if SIDE = 'R'.

Here is the call graph for this function:

la_dorm2r()

pure subroutine, public la_lapack_d::la_dorm2r	(	character, intent(in)	side,
		character, intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DORM2R: overwrites the general real m by n matrix C with Q * C if SIDE = 'L' and TRANS = 'N', or Q**T* C if SIDE = 'L' and TRANS = 'T', or C * Q if SIDE = 'R' and TRANS = 'N', or C * Q**T if SIDE = 'R' and TRANS = 'T', where Q is a real orthogonal matrix defined as the product of k elementary reflectors Q = H(1) H(2) . . . H(k) as returned by DGEQRF. Q is of order m if SIDE = 'L' and of order n if SIDE = 'R'.

Here is the call graph for this function:

la_dormbr()

pure subroutine, public la_lapack_d::la_dormbr	(	character, intent(in)	vect,
		character, intent(in)	side,
		character, intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

If VECT = 'Q', DORMBR: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q * C C * Q TRANS = 'T': Q**T * C C * Q**T If VECT = 'P', DORMBR overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': P * C C * P TRANS = 'T': P**T * C C * P**T Here Q and P**T are the orthogonal matrices determined by DGEBRD when reducing a real matrix A to bidiagonal form: A = Q * B * P**T. Q and P**T are defined as products of elementary reflectors H(i) and G(i) respectively. Let nq = m if SIDE = 'L' and nq = n if SIDE = 'R'. Thus nq is the order of the orthogonal matrix Q or P**T that is applied. If VECT = 'Q', A is assumed to have been an NQ-by-K matrix: if nq >= k, Q = H(1) H(2) . . . H(k); if nq < k, Q = H(1) H(2) . . . H(nq-1). If VECT = 'P', A is assumed to have been a K-by-NQ matrix: if k < nq, P = G(1) G(2) . . . G(k); if k >= nq, P = G(1) G(2) . . . G(nq-1).

Here is the call graph for this function:

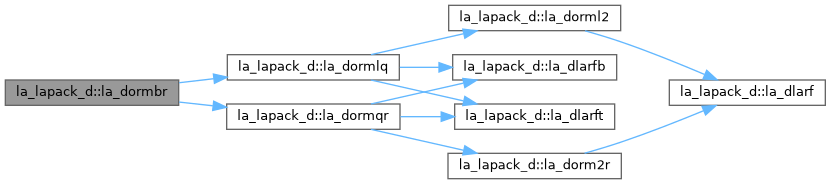
la_dormhr()

pure subroutine, public la_lapack_d::la_dormhr	(	character, intent(in)	side,
		character, intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ilo,
		integer(ilp), intent(in)	ihi,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DORMHR: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q * C C * Q TRANS = 'T': Q**T * C C * Q**T where Q is a real orthogonal matrix of order nq, with nq = m if SIDE = 'L' and nq = n if SIDE = 'R'. Q is defined as the product of IHI-ILO elementary reflectors, as returned by DGEHRD: Q = H(ilo) H(ilo+1) . . . H(ihi-1).

Here is the call graph for this function:

la_dorml2()

pure subroutine, public la_lapack_d::la_dorml2	(	character, intent(in)	side,
		character, intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DORML2: overwrites the general real m by n matrix C with Q * C if SIDE = 'L' and TRANS = 'N', or Q**T* C if SIDE = 'L' and TRANS = 'T', or C * Q if SIDE = 'R' and TRANS = 'N', or C * Q**T if SIDE = 'R' and TRANS = 'T', where Q is a real orthogonal matrix defined as the product of k elementary reflectors Q = H(k) . . . H(2) H(1) as returned by DGELQF. Q is of order m if SIDE = 'L' and of order n if SIDE = 'R'.

Here is the call graph for this function:

la_dormlq()

pure subroutine, public la_lapack_d::la_dormlq	(	character, intent(in)	side,
		character, intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DORMLQ: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q * C C * Q TRANS = 'T': Q**T * C C * Q**T where Q is a real orthogonal matrix defined as the product of k elementary reflectors Q = H(k) . . . H(2) H(1) as returned by DGELQF. Q is of order M if SIDE = 'L' and of order N if SIDE = 'R'.

Here is the call graph for this function:

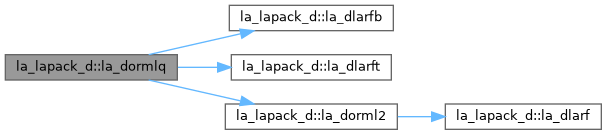
la_dormql()

pure subroutine, public la_lapack_d::la_dormql	(	character, intent(in)	side,
		character, intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DORMQL: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q * C C * Q TRANS = 'T': Q**T * C C * Q**T where Q is a real orthogonal matrix defined as the product of k elementary reflectors Q = H(k) . . . H(2) H(1) as returned by DGEQLF. Q is of order M if SIDE = 'L' and of order N if SIDE = 'R'.

Here is the call graph for this function:

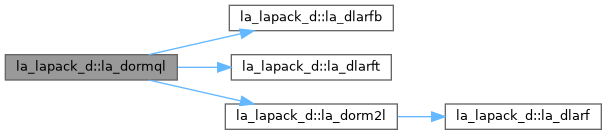
la_dormqr()

pure subroutine, public la_lapack_d::la_dormqr	(	character, intent(in)	side,
		character, intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DORMQR: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q * C C * Q TRANS = 'T': Q**T * C C * Q**T where Q is a real orthogonal matrix defined as the product of k elementary reflectors Q = H(1) H(2) . . . H(k) as returned by DGEQRF. Q is of order M if SIDE = 'L' and of order N if SIDE = 'R'.

Here is the call graph for this function:

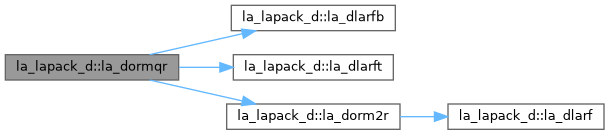
la_dormr2()

pure subroutine, public la_lapack_d::la_dormr2	(	character, intent(in)	side,
		character, intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DORMR2: overwrites the general real m by n matrix C with Q * C if SIDE = 'L' and TRANS = 'N', or Q**T* C if SIDE = 'L' and TRANS = 'T', or C * Q if SIDE = 'R' and TRANS = 'N', or C * Q**T if SIDE = 'R' and TRANS = 'T', where Q is a real orthogonal matrix defined as the product of k elementary reflectors Q = H(1) H(2) . . . H(k) as returned by DGERQF. Q is of order m if SIDE = 'L' and of order n if SIDE = 'R'.

Here is the call graph for this function:

la_dormr3()

pure subroutine, public la_lapack_d::la_dormr3	(	character, intent(in)	side,
		character, intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		integer(ilp), intent(in)	l,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DORMR3: overwrites the general real m by n matrix C with Q * C if SIDE = 'L' and TRANS = 'N', or Q**T* C if SIDE = 'L' and TRANS = 'C', or C * Q if SIDE = 'R' and TRANS = 'N', or C * Q**T if SIDE = 'R' and TRANS = 'C', where Q is a real orthogonal matrix defined as the product of k elementary reflectors Q = H(1) H(2) . . . H(k) as returned by DTZRZF. Q is of order m if SIDE = 'L' and of order n if SIDE = 'R'.

Here is the call graph for this function:

la_dormrq()

pure subroutine, public la_lapack_d::la_dormrq	(	character, intent(in)	side,
		character, intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DORMRQ: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q * C C * Q TRANS = 'T': Q**T * C C * Q**T where Q is a real orthogonal matrix defined as the product of k elementary reflectors Q = H(1) H(2) . . . H(k) as returned by DGERQF. Q is of order M if SIDE = 'L' and of order N if SIDE = 'R'.

Here is the call graph for this function:

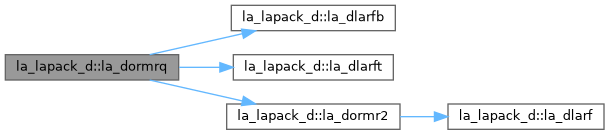
la_dormrz()

pure subroutine, public la_lapack_d::la_dormrz	(	character, intent(in)	side,
		character, intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		integer(ilp), intent(in)	l,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DORMRZ: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q * C C * Q TRANS = 'T': Q**T * C C * Q**T where Q is a real orthogonal matrix defined as the product of k elementary reflectors Q = H(1) H(2) . . . H(k) as returned by DTZRZF. Q is of order M if SIDE = 'L' and of order N if SIDE = 'R'.

Here is the call graph for this function:

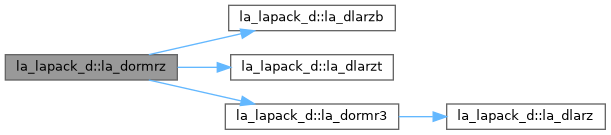
la_dormtr()

pure subroutine, public la_lapack_d::la_dormtr	(	character, intent(in)	side,
		character, intent(in)	uplo,
		character, intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	tau,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DORMTR: overwrites the general real M-by-N matrix C with SIDE = 'L' SIDE = 'R' TRANS = 'N': Q * C C * Q TRANS = 'T': Q**T * C C * Q**T where Q is a real orthogonal matrix of order nq, with nq = m if SIDE = 'L' and nq = n if SIDE = 'R'. Q is defined as the product of nq-1 elementary reflectors, as returned by DSYTRD: if UPLO = 'U', Q = H(nq-1) . . . H(2) H(1); if UPLO = 'L', Q = H(1) H(2) . . . H(nq-1).

Here is the call graph for this function:

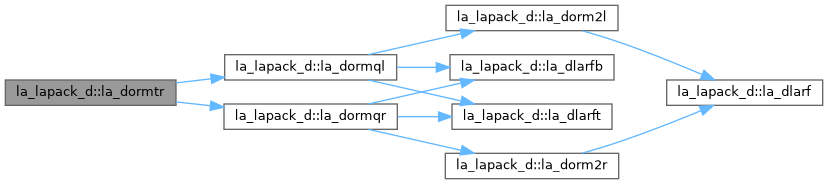
la_dpbcon()

pure subroutine, public la_lapack_d::la_dpbcon	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kd,
		real(dp), dimension(ldab,*), intent(in)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), intent(in)	anorm,
		real(dp), intent(out)	rcond,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DPBCON: estimates the reciprocal of the condition number (in the 1-norm) of a real symmetric positive definite band matrix using the Cholesky factorization A = U**T*U or A = L*L**T computed by DPBTRF. An estimate is obtained for norm(inv(A)), and the reciprocal of the condition number is computed as RCOND = 1 / (ANORM * norm(inv(A))).

Here is the call graph for this function:

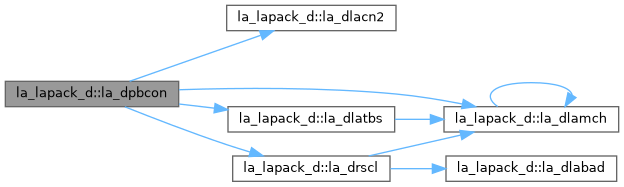
la_dpbequ()

pure subroutine, public la_lapack_d::la_dpbequ	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kd,
		real(dp), dimension(ldab,*), intent(in)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(*), intent(out)	s,
		real(dp), intent(out)	scond,
		real(dp), intent(out)	amax,
		integer(ilp), intent(out)	info
	)

DPBEQU: computes row and column scalings intended to equilibrate a symmetric positive definite band matrix A and reduce its condition number (with respect to the two-norm). S contains the scale factors, S(i) = 1/sqrt(A(i,i)), chosen so that the scaled matrix B with elements B(i,j) = S(i)*A(i,j)*S(j) has ones on the diagonal. This choice of S puts the condition number of B within a factor N of the smallest possible condition number over all possible diagonal scalings.

la_dpbrfs()

pure subroutine, public la_lapack_d::la_dpbrfs	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kd,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(ldab,*), intent(in)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(ldafb,*), intent(in)	afb,
		integer(ilp), intent(in)	ldafb,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldx,*), intent(inout)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), dimension(*), intent(out)	ferr,
		real(dp), dimension(*), intent(out)	berr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DPBRFS: improves the computed solution to a system of linear equations when the coefficient matrix is symmetric positive definite and banded, and provides error bounds and backward error estimates for the solution.

Here is the call graph for this function:

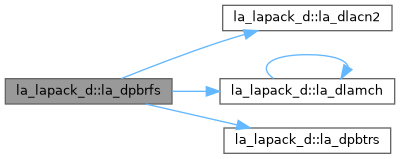
la_dpbstf()

pure subroutine, public la_lapack_d::la_dpbstf	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kd,
		real(dp), dimension(ldab,*), intent(inout)	ab,
		integer(ilp), intent(in)	ldab,
		integer(ilp), intent(out)	info
	)

DPBSTF: computes a split Cholesky factorization of a real symmetric positive definite band matrix A. This routine is designed to be used in conjunction with DSBGST. The factorization has the form A = S**T*S where S is a band matrix of the same bandwidth as A and the following structure: S = ( U ) ( M L ) where U is upper triangular of order m = (n+kd)/2, and L is lower triangular of order n-m.

la_dpbsv()

pure subroutine, public la_lapack_d::la_dpbsv	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kd,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(ldab,*), intent(inout)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	info
	)

DPBSV: computes the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric positive definite band matrix and X and B are N-by-NRHS matrices. The Cholesky decomposition is used to factor A as A = U**T * U, if UPLO = 'U', or A = L * L**T, if UPLO = 'L', where U is an upper triangular band matrix, and L is a lower triangular band matrix, with the same number of superdiagonals or subdiagonals as A. The factored form of A is then used to solve the system of equations A * X = B.

Here is the call graph for this function:

la_dpbsvx()

subroutine, public la_lapack_d::la_dpbsvx	(	character, intent(in)	fact,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kd,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(ldab,*), intent(inout)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(ldafb,*), intent(inout)	afb,
		integer(ilp), intent(in)	ldafb,
		character, intent(inout)	equed,
		real(dp), dimension(*), intent(inout)	s,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldx,*), intent(out)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), intent(out)	rcond,
		real(dp), dimension(*), intent(out)	ferr,
		real(dp), dimension(*), intent(out)	berr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DPBSVX: uses the Cholesky factorization A = U**T*U or A = L*L**T to compute the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric positive definite band matrix and X and B are N-by-NRHS matrices. Error bounds on the solution and a condition estimate are also provided.

Here is the call graph for this function:

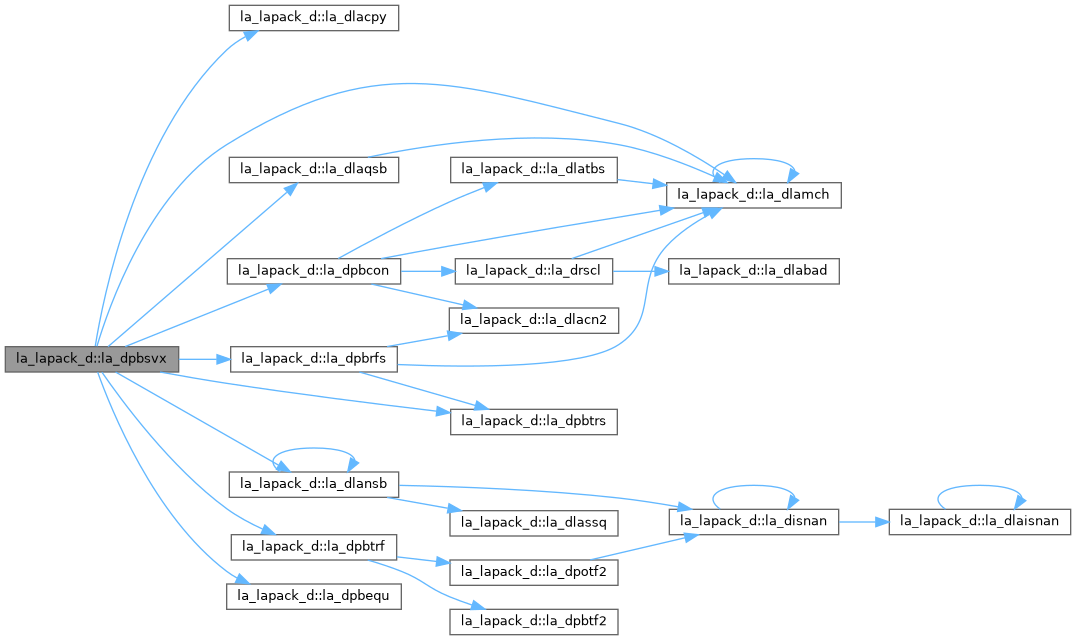
la_dpbtf2()

pure subroutine, public la_lapack_d::la_dpbtf2	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kd,
		real(dp), dimension(ldab,*), intent(inout)	ab,
		integer(ilp), intent(in)	ldab,
		integer(ilp), intent(out)	info
	)

DPBTF2: computes the Cholesky factorization of a real symmetric positive definite band matrix A. The factorization has the form A = U**T * U , if UPLO = 'U', or A = L * L**T, if UPLO = 'L', where U is an upper triangular matrix, U**T is the transpose of U, and L is lower triangular. This is the unblocked version of the algorithm, calling Level 2 BLAS.

la_dpbtrf()

pure subroutine, public la_lapack_d::la_dpbtrf	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kd,
		real(dp), dimension(ldab,*), intent(inout)	ab,
		integer(ilp), intent(in)	ldab,
		integer(ilp), intent(out)	info
	)

DPBTRF: computes the Cholesky factorization of a real symmetric positive definite band matrix A. The factorization has the form A = U**T * U, if UPLO = 'U', or A = L * L**T, if UPLO = 'L', where U is an upper triangular matrix and L is lower triangular.

Here is the call graph for this function:

la_dpbtrs()

pure subroutine, public la_lapack_d::la_dpbtrs	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kd,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(ldab,*), intent(in)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	info
	)

DPBTRS: solves a system of linear equations A*X = B with a symmetric positive definite band matrix A using the Cholesky factorization A = U**T*U or A = L*L**T computed by DPBTRF.

la_dpftrf()

pure subroutine, public la_lapack_d::la_dpftrf	(	character, intent(in)	transr,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(0:*), intent(inout)	a,
		integer(ilp), intent(out)	info
	)

DPFTRF: computes the Cholesky factorization of a real symmetric positive definite matrix A. The factorization has the form A = U**T * U, if UPLO = 'U', or A = L * L**T, if UPLO = 'L', where U is an upper triangular matrix and L is lower triangular. This is the block version of the algorithm, calling Level 3 BLAS.

Here is the call graph for this function:

la_dpftri()

pure subroutine, public la_lapack_d::la_dpftri	(	character, intent(in)	transr,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(0:*), intent(inout)	a,
		integer(ilp), intent(out)	info
	)

DPFTRI: computes the inverse of a (real) symmetric positive definite matrix A using the Cholesky factorization A = U**T*U or A = L*L**T computed by DPFTRF.

Here is the call graph for this function:

la_dpftrs()

pure subroutine, public la_lapack_d::la_dpftrs	(	character, intent(in)	transr,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(0:*), intent(in)	a,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	info
	)

DPFTRS: solves a system of linear equations A*X = B with a symmetric positive definite matrix A using the Cholesky factorization A = U**T*U or A = L*L**T computed by DPFTRF.

Here is the call graph for this function:

la_dpocon()

pure subroutine, public la_lapack_d::la_dpocon	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), intent(in)	anorm,
		real(dp), intent(out)	rcond,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DPOCON: estimates the reciprocal of the condition number (in the 1-norm) of a real symmetric positive definite matrix using the Cholesky factorization A = U**T*U or A = L*L**T computed by DPOTRF. An estimate is obtained for norm(inv(A)), and the reciprocal of the condition number is computed as RCOND = 1 / (ANORM * norm(inv(A))).

Here is the call graph for this function:

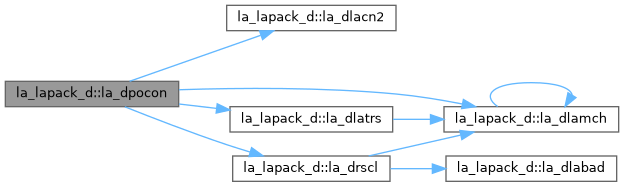
la_dpoequ()

pure subroutine, public la_lapack_d::la_dpoequ	(	integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	s,
		real(dp), intent(out)	scond,
		real(dp), intent(out)	amax,
		integer(ilp), intent(out)	info
	)

DPOEQU: computes row and column scalings intended to equilibrate a symmetric positive definite matrix A and reduce its condition number (with respect to the two-norm). S contains the scale factors, S(i) = 1/sqrt(A(i,i)), chosen so that the scaled matrix B with elements B(i,j) = S(i)*A(i,j)*S(j) has ones on the diagonal. This choice of S puts the condition number of B within a factor N of the smallest possible condition number over all possible diagonal scalings.

la_dpoequb()

pure subroutine, public la_lapack_d::la_dpoequb	(	integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	s,
		real(dp), intent(out)	scond,
		real(dp), intent(out)	amax,
		integer(ilp), intent(out)	info
	)

DPOEQUB: computes row and column scalings intended to equilibrate a symmetric positive definite matrix A and reduce its condition number (with respect to the two-norm). S contains the scale factors, S(i) = 1/sqrt(A(i,i)), chosen so that the scaled matrix B with elements B(i,j) = S(i)*A(i,j)*S(j) has ones on the diagonal. This choice of S puts the condition number of B within a factor N of the smallest possible condition number over all possible diagonal scalings. This routine differs from DPOEQU by restricting the scaling factors to a power of the radix. Barring over- and underflow, scaling by these factors introduces no additional rounding errors. However, the scaled diagonal entries are no longer approximately 1 but lie between sqrt(radix) and 1/sqrt(radix).

Here is the call graph for this function:

la_dporfs()

pure subroutine, public la_lapack_d::la_dporfs	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldaf,*), intent(in)	af,
		integer(ilp), intent(in)	ldaf,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldx,*), intent(inout)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), dimension(*), intent(out)	ferr,
		real(dp), dimension(*), intent(out)	berr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DPORFS: improves the computed solution to a system of linear equations when the coefficient matrix is symmetric positive definite, and provides error bounds and backward error estimates for the solution.

Here is the call graph for this function:

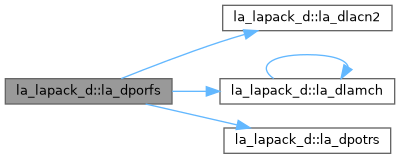
la_dposv()

pure subroutine, public la_lapack_d::la_dposv	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	info
	)

DPOSV: computes the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric positive definite matrix and X and B are N-by-NRHS matrices. The Cholesky decomposition is used to factor A as A = U**T* U, if UPLO = 'U', or A = L * L**T, if UPLO = 'L', where U is an upper triangular matrix and L is a lower triangular matrix. The factored form of A is then used to solve the system of equations A * X = B.

Here is the call graph for this function:

la_dposvx()

subroutine, public la_lapack_d::la_dposvx	(	character, intent(in)	fact,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldaf,*), intent(inout)	af,
		integer(ilp), intent(in)	ldaf,
		character, intent(inout)	equed,
		real(dp), dimension(*), intent(inout)	s,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldx,*), intent(out)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), intent(out)	rcond,
		real(dp), dimension(*), intent(out)	ferr,
		real(dp), dimension(*), intent(out)	berr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DPOSVX: uses the Cholesky factorization A = U**T*U or A = L*L**T to compute the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric positive definite matrix and X and B are N-by-NRHS matrices. Error bounds on the solution and a condition estimate are also provided.

Here is the call graph for this function:

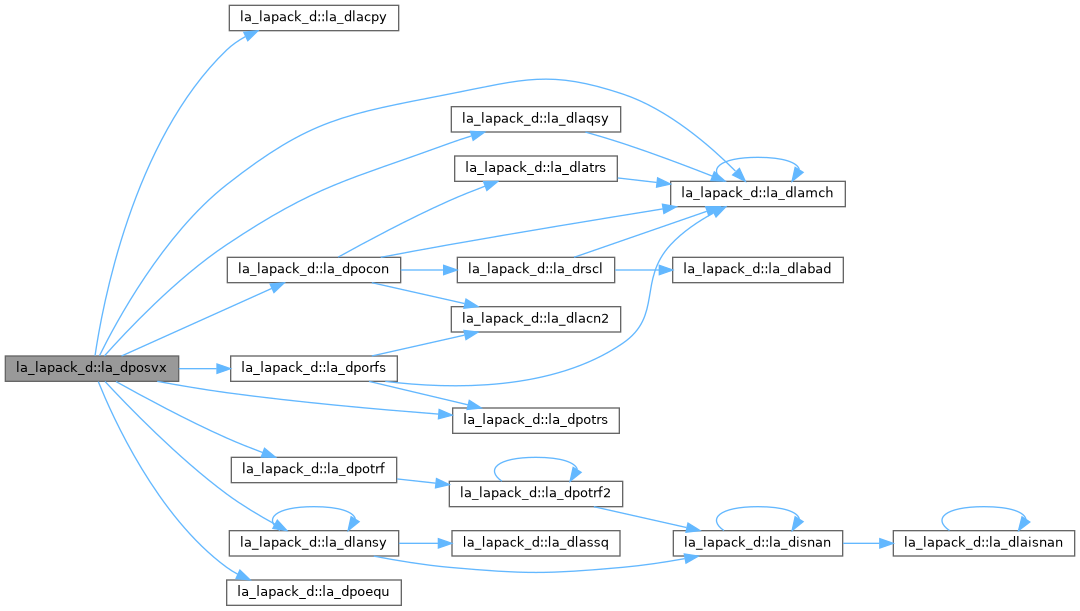
la_dpotf2()

pure subroutine, public la_lapack_d::la_dpotf2	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), intent(out)	info
	)

DPOTF2: computes the Cholesky factorization of a real symmetric positive definite matrix A. The factorization has the form A = U**T * U , if UPLO = 'U', or A = L * L**T, if UPLO = 'L', where U is an upper triangular matrix and L is lower triangular. This is the unblocked version of the algorithm, calling Level 2 BLAS.

Here is the call graph for this function:

la_dpotrf()

pure subroutine, public la_lapack_d::la_dpotrf	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), intent(out)	info
	)

DPOTRF: computes the Cholesky factorization of a real symmetric positive definite matrix A. The factorization has the form A = U**T * U, if UPLO = 'U', or A = L * L**T, if UPLO = 'L', where U is an upper triangular matrix and L is lower triangular. This is the block version of the algorithm, calling Level 3 BLAS.

Here is the call graph for this function:

la_dpotrf2()

pure recursive subroutine, public la_lapack_d::la_dpotrf2	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), intent(out)	info
	)

DPOTRF2: computes the Cholesky factorization of a real symmetric positive definite matrix A using the recursive algorithm. The factorization has the form A = U**T * U, if UPLO = 'U', or A = L * L**T, if UPLO = 'L', where U is an upper triangular matrix and L is lower triangular. This is the recursive version of the algorithm. It divides the matrix into four submatrices: [ A11 | A12 ] where A11 is n1 by n1 and A22 is n2 by n2 A = [ --—|--— ] with n1 = n/2 [ A21 | A22 ] n2 = n-n1 The subroutine calls itself to factor A11. Update and scale A21 or A12, update A22 then calls itself to factor A22.

Here is the call graph for this function:

la_dpotri()

pure subroutine, public la_lapack_d::la_dpotri	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), intent(out)	info
	)

DPOTRI: computes the inverse of a real symmetric positive definite matrix A using the Cholesky factorization A = U**T*U or A = L*L**T computed by DPOTRF.

Here is the call graph for this function:

la_dpotrs()

pure subroutine, public la_lapack_d::la_dpotrs	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	info
	)

DPOTRS: solves a system of linear equations A*X = B with a symmetric positive definite matrix A using the Cholesky factorization A = U**T*U or A = L*L**T computed by DPOTRF.

la_dppcon()

pure subroutine, public la_lapack_d::la_dppcon	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(in)	ap,
		real(dp), intent(in)	anorm,
		real(dp), intent(out)	rcond,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DPPCON: estimates the reciprocal of the condition number (in the 1-norm) of a real symmetric positive definite packed matrix using the Cholesky factorization A = U**T*U or A = L*L**T computed by DPPTRF. An estimate is obtained for norm(inv(A)), and the reciprocal of the condition number is computed as RCOND = 1 / (ANORM * norm(inv(A))).

Here is the call graph for this function:

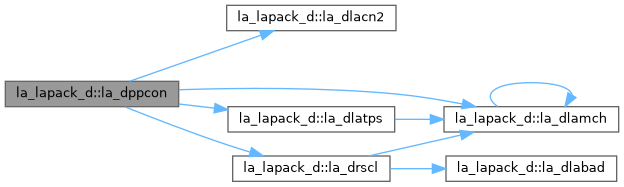
la_dppequ()

pure subroutine, public la_lapack_d::la_dppequ	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(in)	ap,
		real(dp), dimension(*), intent(out)	s,
		real(dp), intent(out)	scond,
		real(dp), intent(out)	amax,
		integer(ilp), intent(out)	info
	)

DPPEQU: computes row and column scalings intended to equilibrate a symmetric positive definite matrix A in packed storage and reduce its condition number (with respect to the two-norm). S contains the scale factors, S(i)=1/sqrt(A(i,i)), chosen so that the scaled matrix B with elements B(i,j)=S(i)*A(i,j)*S(j) has ones on the diagonal. This choice of S puts the condition number of B within a factor N of the smallest possible condition number over all possible diagonal scalings.

la_dpprfs()

pure subroutine, public la_lapack_d::la_dpprfs	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(*), intent(in)	ap,
		real(dp), dimension(*), intent(in)	afp,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldx,*), intent(inout)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), dimension(*), intent(out)	ferr,
		real(dp), dimension(*), intent(out)	berr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DPPRFS: improves the computed solution to a system of linear equations when the coefficient matrix is symmetric positive definite and packed, and provides error bounds and backward error estimates for the solution.

Here is the call graph for this function:

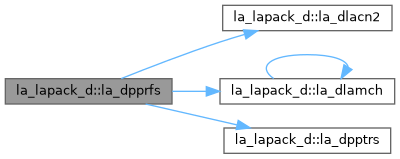
la_dppsv()

pure subroutine, public la_lapack_d::la_dppsv	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(*), intent(inout)	ap,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	info
	)

DPPSV: computes the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric positive definite matrix stored in packed format and X and B are N-by-NRHS matrices. The Cholesky decomposition is used to factor A as A = U**T* U, if UPLO = 'U', or A = L * L**T, if UPLO = 'L', where U is an upper triangular matrix and L is a lower triangular matrix. The factored form of A is then used to solve the system of equations A * X = B.

Here is the call graph for this function:

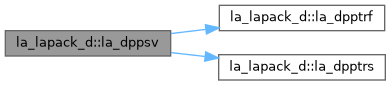
la_dppsvx()

subroutine, public la_lapack_d::la_dppsvx	(	character, intent(in)	fact,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(*), intent(inout)	ap,
		real(dp), dimension(*), intent(inout)	afp,
		character, intent(inout)	equed,
		real(dp), dimension(*), intent(inout)	s,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldx,*), intent(out)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), intent(out)	rcond,
		real(dp), dimension(*), intent(out)	ferr,
		real(dp), dimension(*), intent(out)	berr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DPPSVX: uses the Cholesky factorization A = U**T*U or A = L*L**T to compute the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric positive definite matrix stored in packed format and X and B are N-by-NRHS matrices. Error bounds on the solution and a condition estimate are also provided.

Here is the call graph for this function:

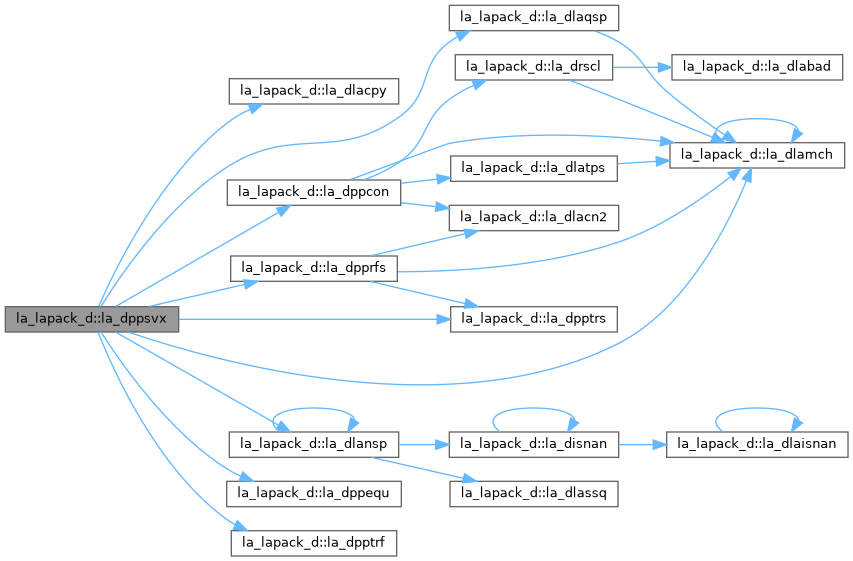
la_dpptrf()

pure subroutine, public la_lapack_d::la_dpptrf	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	ap,
		integer(ilp), intent(out)	info
	)

DPPTRF: computes the Cholesky factorization of a real symmetric positive definite matrix A stored in packed format. The factorization has the form A = U**T * U, if UPLO = 'U', or A = L * L**T, if UPLO = 'L', where U is an upper triangular matrix and L is lower triangular.

la_dpptri()

pure subroutine, public la_lapack_d::la_dpptri	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	ap,
		integer(ilp), intent(out)	info
	)

DPPTRI: computes the inverse of a real symmetric positive definite matrix A using the Cholesky factorization A = U**T*U or A = L*L**T computed by DPPTRF.

Here is the call graph for this function:

la_dpptrs()

pure subroutine, public la_lapack_d::la_dpptrs	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(*), intent(in)	ap,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	info
	)

DPPTRS: solves a system of linear equations A*X = B with a symmetric positive definite matrix A in packed storage using the Cholesky factorization A = U**T*U or A = L*L**T computed by DPPTRF.

la_dpstf2()

pure subroutine, public la_lapack_d::la_dpstf2	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(n), intent(out)	piv,
		integer(ilp), intent(out)	rank,
		real(dp), intent(in)	tol,
		real(dp), dimension(2*n), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DPSTF2: computes the Cholesky factorization with complete pivoting of a real symmetric positive semidefinite matrix A. The factorization has the form P**T * A * P = U**T * U , if UPLO = 'U', P**T * A * P = L * L**T, if UPLO = 'L', where U is an upper triangular matrix and L is lower triangular, and P is stored as vector PIV. This algorithm does not attempt to check that A is positive semidefinite. This version of the algorithm calls level 2 BLAS.

Here is the call graph for this function:

la_dpstrf()

pure subroutine, public la_lapack_d::la_dpstrf	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(n), intent(out)	piv,
		integer(ilp), intent(out)	rank,
		real(dp), intent(in)	tol,
		real(dp), dimension(2*n), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DPSTRF: computes the Cholesky factorization with complete pivoting of a real symmetric positive semidefinite matrix A. The factorization has the form P**T * A * P = U**T * U , if UPLO = 'U', P**T * A * P = L * L**T, if UPLO = 'L', where U is an upper triangular matrix and L is lower triangular, and P is stored as vector PIV. This algorithm does not attempt to check that A is positive semidefinite. This version of the algorithm calls level 3 BLAS.

Here is the call graph for this function:

la_dptcon()

pure subroutine, public la_lapack_d::la_dptcon	(	integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(in)	e,
		real(dp), intent(in)	anorm,
		real(dp), intent(out)	rcond,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DPTCON: computes the reciprocal of the condition number (in the 1-norm) of a real symmetric positive definite tridiagonal matrix using the factorization A = L*D*L**T or A = U**T*D*U computed by DPTTRF. Norm(inv(A)) is computed by a direct method, and the reciprocal of the condition number is computed as RCOND = 1 / (ANORM * norm(inv(A))).

la_dpteqr()

pure subroutine, public la_lapack_d::la_dpteqr	(	character, intent(in)	compz,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(inout)	e,
		real(dp), dimension(ldz,*), intent(inout)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DPTEQR: computes all eigenvalues and, optionally, eigenvectors of a symmetric positive definite tridiagonal matrix by first factoring the matrix using DPTTRF, and then calling DBDSQR to compute the singular values of the bidiagonal factor. This routine computes the eigenvalues of the positive definite tridiagonal matrix to high relative accuracy. This means that if the eigenvalues range over many orders of magnitude in size, then the small eigenvalues and corresponding eigenvectors will be computed more accurately than, for example, with the standard QR method. The eigenvectors of a full or band symmetric positive definite matrix can also be found if DSYTRD, DSPTRD, or DSBTRD has been used to reduce this matrix to tridiagonal form. (The reduction to tridiagonal form, however, may preclude the possibility of obtaining high relative accuracy in the small eigenvalues of the original matrix, if these eigenvalues range over many orders of magnitude.)

Here is the call graph for this function:

la_dptrfs()

pure subroutine, public la_lapack_d::la_dptrfs	(	integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(in)	e,
		real(dp), dimension(*), intent(in)	df,
		real(dp), dimension(*), intent(in)	ef,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldx,*), intent(inout)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), dimension(*), intent(out)	ferr,
		real(dp), dimension(*), intent(out)	berr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DPTRFS: improves the computed solution to a system of linear equations when the coefficient matrix is symmetric positive definite and tridiagonal, and provides error bounds and backward error estimates for the solution.

Here is the call graph for this function:

la_dptsv()

pure subroutine, public la_lapack_d::la_dptsv	(	integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(inout)	e,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	info
	)

DPTSV: computes the solution to a real system of linear equations A*X = B, where A is an N-by-N symmetric positive definite tridiagonal matrix, and X and B are N-by-NRHS matrices. A is factored as A = L*D*L**T, and the factored form of A is then used to solve the system of equations.

Here is the call graph for this function:

la_dptsvx()

pure subroutine, public la_lapack_d::la_dptsvx	(	character, intent(in)	fact,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(in)	e,
		real(dp), dimension(*), intent(inout)	df,
		real(dp), dimension(*), intent(inout)	ef,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldx,*), intent(out)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), intent(out)	rcond,
		real(dp), dimension(*), intent(out)	ferr,
		real(dp), dimension(*), intent(out)	berr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DPTSVX: uses the factorization A = L*D*L**T to compute the solution to a real system of linear equations A*X = B, where A is an N-by-N symmetric positive definite tridiagonal matrix and X and B are N-by-NRHS matrices. Error bounds on the solution and a condition estimate are also provided.

Here is the call graph for this function:

la_dpttrf()

pure subroutine, public la_lapack_d::la_dpttrf	(	integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(inout)	e,
		integer(ilp), intent(out)	info
	)

DPTTRF: computes the L*D*L**T factorization of a real symmetric positive definite tridiagonal matrix A. The factorization may also be regarded as having the form A = U**T*D*U.

la_dpttrs()

pure subroutine, public la_lapack_d::la_dpttrs	(	integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(in)	e,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	info
	)

DPTTRS: solves a tridiagonal system of the form A * X = B using the L*D*L**T factorization of A computed by DPTTRF. D is a diagonal matrix specified in the vector D, L is a unit bidiagonal matrix whose subdiagonal is specified in the vector E, and X and B are N by NRHS matrices.

Here is the call graph for this function:

la_dptts2()

pure subroutine, public la_lapack_d::la_dptts2	(	integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(in)	e,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb
	)

DPTTS2: solves a tridiagonal system of the form A * X = B using the L*D*L**T factorization of A computed by DPTTRF. D is a diagonal matrix specified in the vector D, L is a unit bidiagonal matrix whose subdiagonal is specified in the vector E, and X and B are N by NRHS matrices.

la_drscl()

pure subroutine, public la_lapack_d::la_drscl	(	integer(ilp), intent(in)	n,
		real(dp), intent(in)	sa,
		real(dp), dimension(*), intent(inout)	sx,
		integer(ilp), intent(in)	incx
	)

DRSCL: multiplies an n-element real vector x by the real scalar 1/a. This is done without overflow or underflow as long as the final result x/a does not overflow or underflow.

Here is the call graph for this function:

la_dsb2st_kernels()

pure subroutine, public la_lapack_d::la_dsb2st_kernels	(	character, intent(in)	uplo,
		logical(lk), intent(in)	wantz,
		integer(ilp), intent(in)	ttype,
		integer(ilp), intent(in)	st,
		integer(ilp), intent(in)	ed,
		integer(ilp), intent(in)	sweep,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nb,
		integer(ilp), intent(in)	ib,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	v,
		real(dp), dimension(*), intent(out)	tau,
		integer(ilp), intent(in)	ldvt,
		real(dp), dimension(*), intent(out)	work
	)

DSB2ST_KERNELS: is an internal routine used by the DSYTRD_SB2ST subroutine.

Here is the call graph for this function:

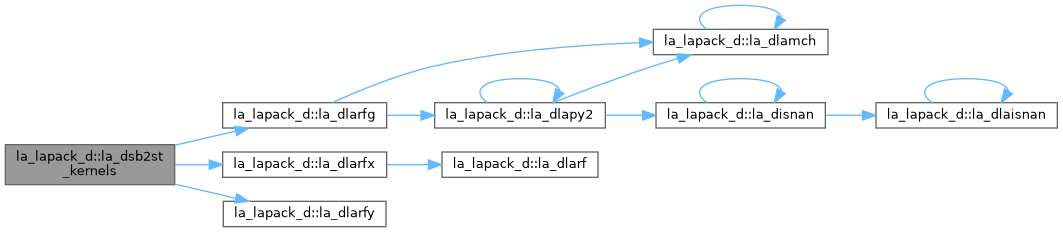
la_dsbev()

subroutine, public la_lapack_d::la_dsbev	(	character, intent(in)	jobz,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kd,
		real(dp), dimension(ldab,*), intent(inout)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(*), intent(out)	w,
		real(dp), dimension(ldz,*), intent(out)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DSBEV: computes all the eigenvalues and, optionally, eigenvectors of a real symmetric band matrix A.

Here is the call graph for this function:

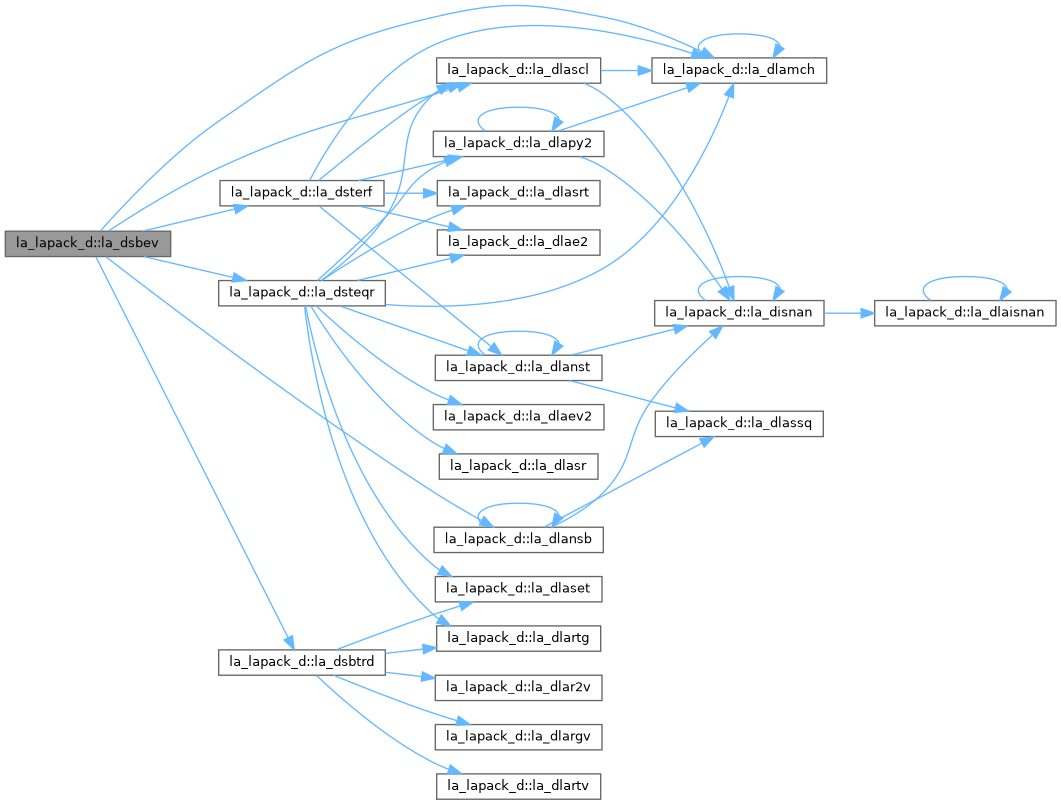
la_dsbevd()

subroutine, public la_lapack_d::la_dsbevd	(	character, intent(in)	jobz,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kd,
		real(dp), dimension(ldab,*), intent(inout)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(*), intent(out)	w,
		real(dp), dimension(ldz,*), intent(out)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(in)	liwork,
		integer(ilp), intent(out)	info
	)

DSBEVD: computes all the eigenvalues and, optionally, eigenvectors of a real symmetric band matrix A. If eigenvectors are desired, it uses a divide and conquer algorithm. The divide and conquer algorithm makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none.

Here is the call graph for this function:

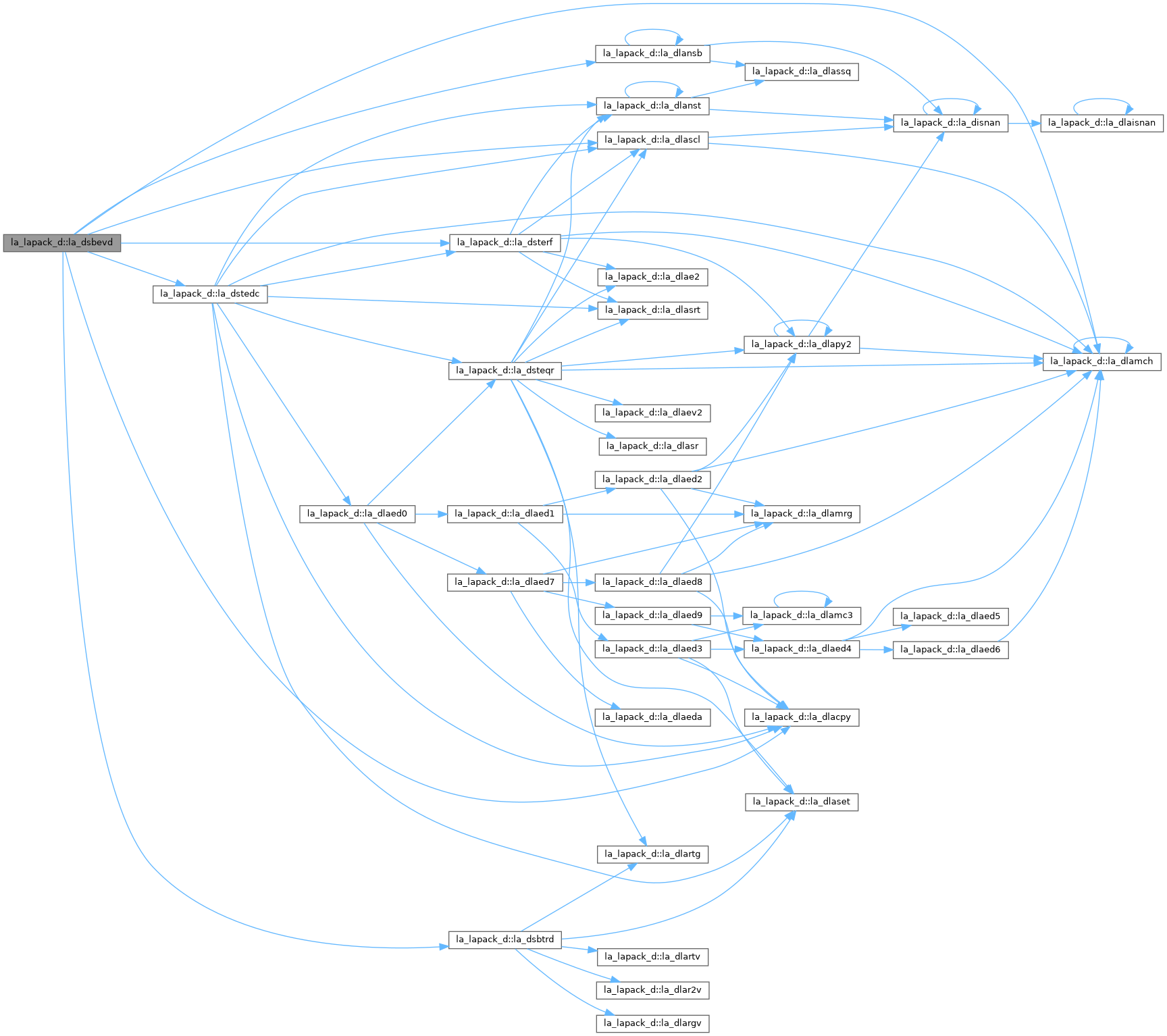
la_dsbevx()

subroutine, public la_lapack_d::la_dsbevx	(	character, intent(in)	jobz,
		character, intent(in)	range,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kd,
		real(dp), dimension(ldab,*), intent(inout)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(ldq,*), intent(out)	q,
		integer(ilp), intent(in)	ldq,
		real(dp), intent(in)	vl,
		real(dp), intent(in)	vu,
		integer(ilp), intent(in)	il,
		integer(ilp), intent(in)	iu,
		real(dp), intent(in)	abstol,
		integer(ilp), intent(out)	m,
		real(dp), dimension(*), intent(out)	w,
		real(dp), dimension(ldz,*), intent(out)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), dimension(*), intent(out)	ifail,
		integer(ilp), intent(out)	info
	)

DSBEVX: computes selected eigenvalues and, optionally, eigenvectors of a real symmetric band matrix A. Eigenvalues and eigenvectors can be selected by specifying either a range of values or a range of indices for the desired eigenvalues.

Here is the call graph for this function:

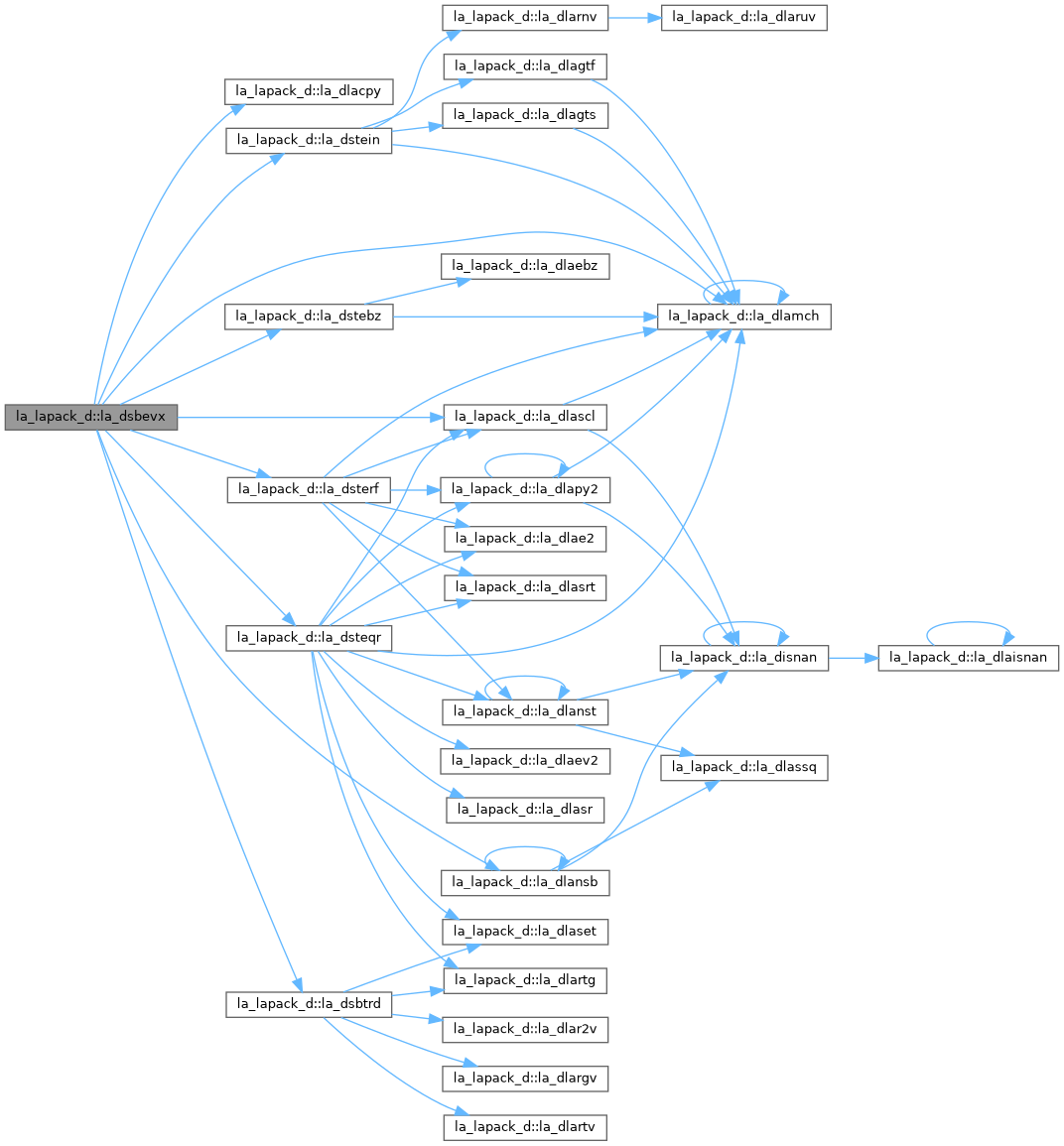
la_dsbgst()

pure subroutine, public la_lapack_d::la_dsbgst	(	character, intent(in)	vect,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ka,
		integer(ilp), intent(in)	kb,
		real(dp), dimension(ldab,*), intent(inout)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(ldbb,*), intent(in)	bb,
		integer(ilp), intent(in)	ldbb,
		real(dp), dimension(ldx,*), intent(out)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DSBGST: reduces a real symmetric-definite banded generalized eigenproblem A*x = lambda*B*x to standard form C*y = lambda*y, such that C has the same bandwidth as A. B must have been previously factorized as S**T*S by DPBSTF, using a split Cholesky factorization. A is overwritten by C = X**T*A*X, where X = S**(-1)*Q and Q is an orthogonal matrix chosen to preserve the bandwidth of A.

Here is the call graph for this function:

la_dsbgv()

pure subroutine, public la_lapack_d::la_dsbgv	(	character, intent(in)	jobz,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ka,
		integer(ilp), intent(in)	kb,
		real(dp), dimension(ldab,*), intent(inout)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(ldbb,*), intent(inout)	bb,
		integer(ilp), intent(in)	ldbb,
		real(dp), dimension(*), intent(out)	w,
		real(dp), dimension(ldz,*), intent(out)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DSBGV: computes all the eigenvalues, and optionally, the eigenvectors of a real generalized symmetric-definite banded eigenproblem, of the form A*x=(lambda)*B*x. Here A and B are assumed to be symmetric and banded, and B is also positive definite.

Here is the call graph for this function:

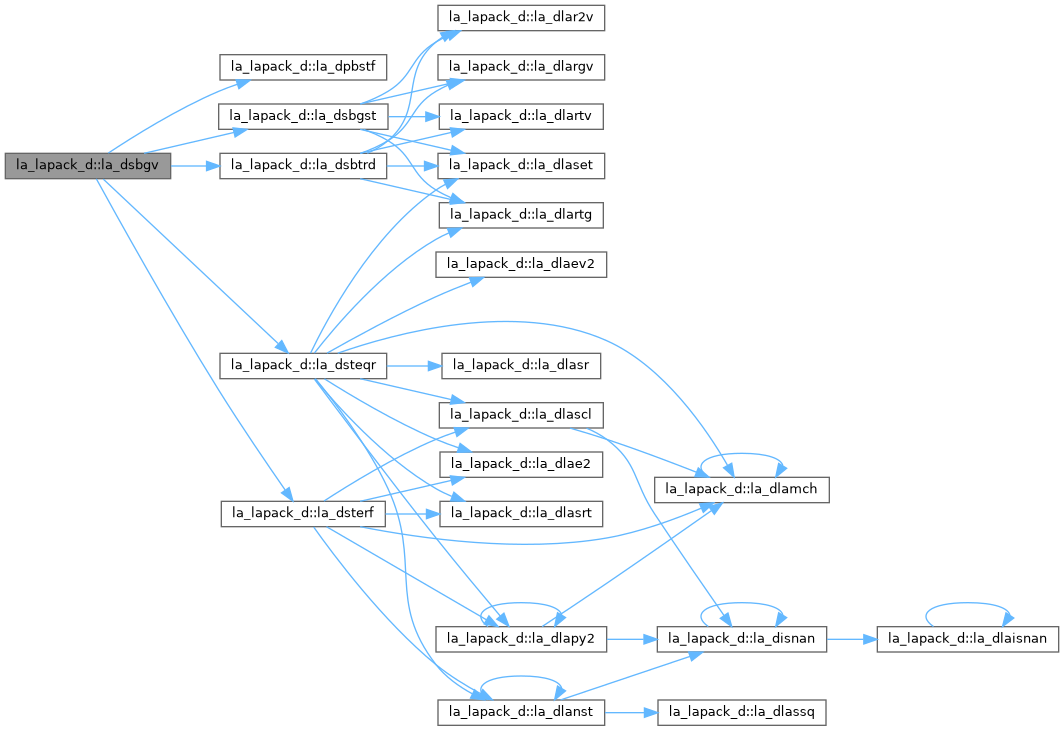
la_dsbgvd()

pure subroutine, public la_lapack_d::la_dsbgvd	(	character, intent(in)	jobz,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ka,
		integer(ilp), intent(in)	kb,
		real(dp), dimension(ldab,*), intent(inout)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(ldbb,*), intent(inout)	bb,
		integer(ilp), intent(in)	ldbb,
		real(dp), dimension(*), intent(out)	w,
		real(dp), dimension(ldz,*), intent(out)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(in)	liwork,
		integer(ilp), intent(out)	info
	)

DSBGVD: computes all the eigenvalues, and optionally, the eigenvectors of a real generalized symmetric-definite banded eigenproblem, of the form A*x=(lambda)*B*x. Here A and B are assumed to be symmetric and banded, and B is also positive definite. If eigenvectors are desired, it uses a divide and conquer algorithm. The divide and conquer algorithm makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none.

Here is the call graph for this function:

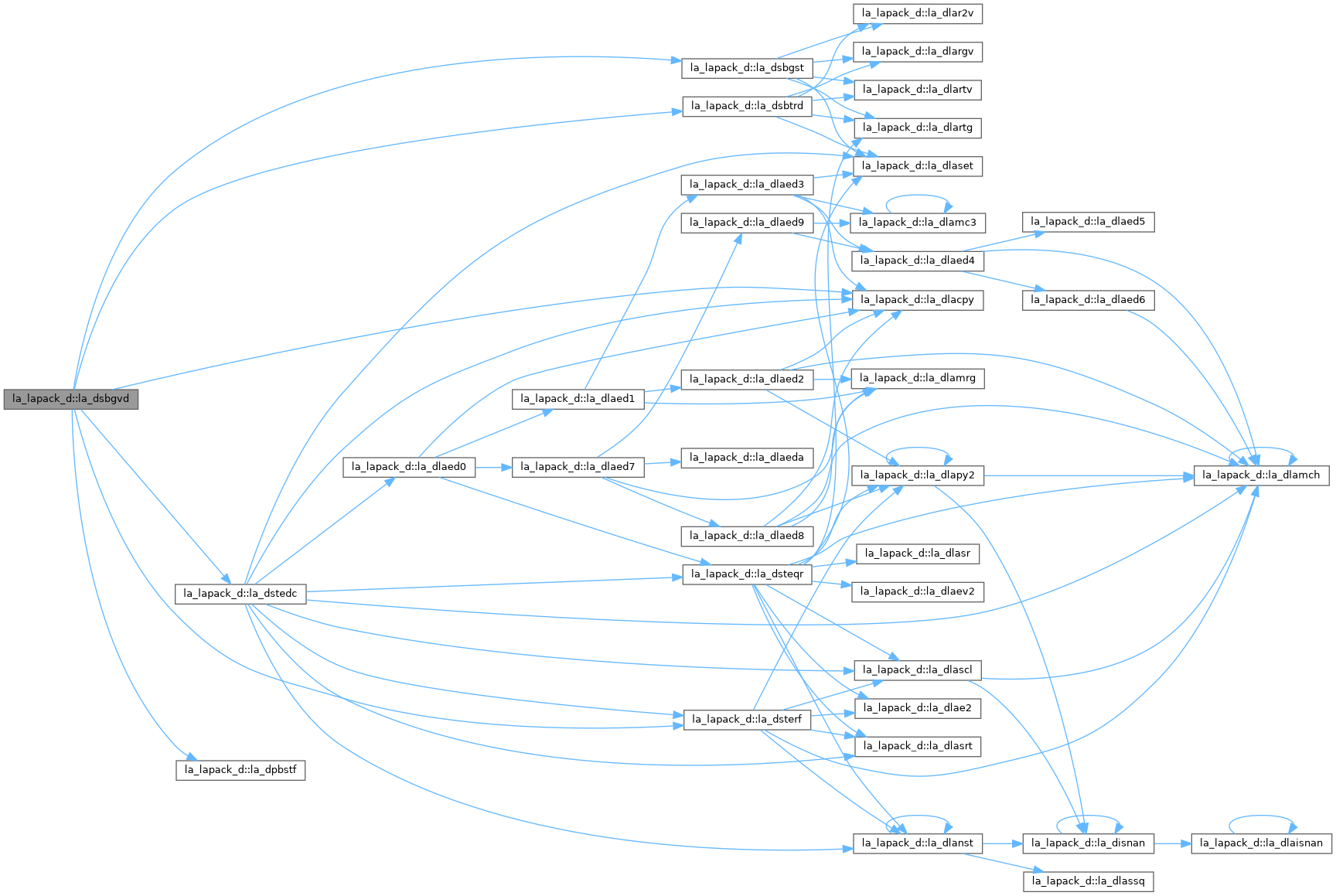
la_dsbgvx()

pure subroutine, public la_lapack_d::la_dsbgvx	(	character, intent(in)	jobz,
		character, intent(in)	range,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ka,
		integer(ilp), intent(in)	kb,
		real(dp), dimension(ldab,*), intent(inout)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(ldbb,*), intent(inout)	bb,
		integer(ilp), intent(in)	ldbb,
		real(dp), dimension(ldq,*), intent(out)	q,
		integer(ilp), intent(in)	ldq,
		real(dp), intent(in)	vl,
		real(dp), intent(in)	vu,
		integer(ilp), intent(in)	il,
		integer(ilp), intent(in)	iu,
		real(dp), intent(in)	abstol,
		integer(ilp), intent(out)	m,
		real(dp), dimension(*), intent(out)	w,
		real(dp), dimension(ldz,*), intent(out)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), dimension(*), intent(out)	ifail,
		integer(ilp), intent(out)	info
	)

DSBGVX: computes selected eigenvalues, and optionally, eigenvectors of a real generalized symmetric-definite banded eigenproblem, of the form A*x=(lambda)*B*x. Here A and B are assumed to be symmetric and banded, and B is also positive definite. Eigenvalues and eigenvectors can be selected by specifying either all eigenvalues, a range of values or a range of indices for the desired eigenvalues.

Here is the call graph for this function:

la_dsbtrd()

pure subroutine, public la_lapack_d::la_dsbtrd	(	character, intent(in)	vect,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kd,
		real(dp), dimension(ldab,*), intent(inout)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(*), intent(out)	d,
		real(dp), dimension(*), intent(out)	e,
		real(dp), dimension(ldq,*), intent(inout)	q,
		integer(ilp), intent(in)	ldq,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DSBTRD: reduces a real symmetric band matrix A to symmetric tridiagonal form T by an orthogonal similarity transformation: Q**T * A * Q = T.

Here is the call graph for this function:

la_dsfrk()

pure subroutine, public la_lapack_d::la_dsfrk	(	character, intent(in)	transr,
		character, intent(in)	uplo,
		character, intent(in)	trans,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		real(dp), intent(in)	alpha,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), intent(in)	beta,
		real(dp), dimension(*), intent(inout)	c
	)

Level 3 BLAS like routine for C in RFP Format. DSFRK: performs one of the symmetric rank–k operations C := alpha*A*A**T + beta*C, or C := alpha*A**T*A + beta*C, where alpha and beta are real scalars, C is an n–by–n symmetric matrix and A is an n–by–k matrix in the first case and a k–by–n matrix in the second case.

la_dsgesv()

subroutine, public la_lapack_d::la_dsgesv	(	integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(out)	ipiv,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldx,*), intent(out)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), dimension(n,*), intent(out)	work,
		real(sp), dimension(*), intent(out)	swork,
		integer(ilp), intent(out)	iter,
		integer(ilp), intent(out)	info
	)

DSGESV: computes the solution to a real system of linear equations A * X = B, where A is an N-by-N matrix and X and B are N-by-NRHS matrices. DSGESV first attempts to factorize the matrix in SINGLE PRECISION and use this factorization within an iterative refinement procedure to produce a solution with DOUBLE PRECISION normwise backward error quality (see below). If the approach fails the method switches to a DOUBLE PRECISION factorization and solve. The iterative refinement is not going to be a winning strategy if the ratio SINGLE PRECISION performance over DOUBLE PRECISION performance is too small. A reasonable strategy should take the number of right-hand sides and the size of the matrix into account. This might be done with a call to ILAENV in the future. Up to now, we always try iterative refinement. The iterative refinement process is stopped if ITER > ITERMAX or for all the RHS we have: RNRM < SQRT(N)*XNRM*ANRM*EPS*BWDMAX where o ITER is the number of the current iteration in the iterative refinement process o RNRM is the infinity-norm of the residual o XNRM is the infinity-norm of the solution o ANRM is the infinity-operator-norm of the matrix A o EPS is the machine epsilon returned by DLAMCH('Epsilon') The value ITERMAX and BWDMAX are fixed to 30 and 1.0D+00 respectively.

Here is the call graph for this function:

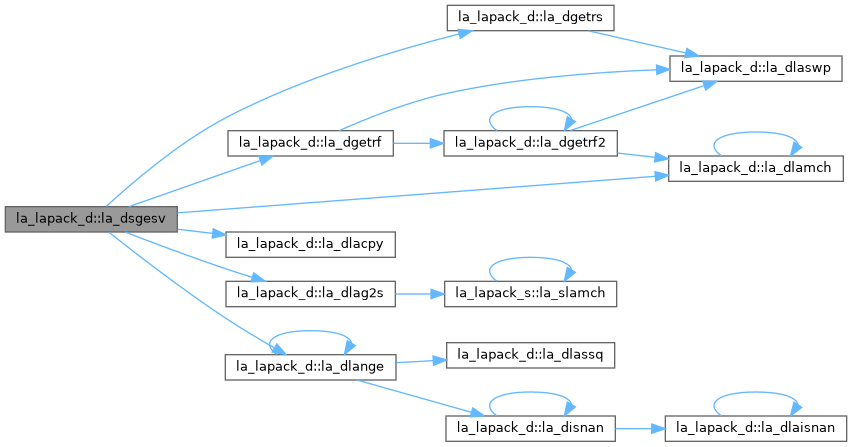
la_dspcon()

pure subroutine, public la_lapack_d::la_dspcon	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(in)	ap,
		integer(ilp), dimension(*), intent(in)	ipiv,
		real(dp), intent(in)	anorm,
		real(dp), intent(out)	rcond,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DSPCON: estimates the reciprocal of the condition number (in the 1-norm) of a real symmetric packed matrix A using the factorization A = U*D*U**T or A = L*D*L**T computed by DSPTRF. An estimate is obtained for norm(inv(A)), and the reciprocal of the condition number is computed as RCOND = 1 / (ANORM * norm(inv(A))).

Here is the call graph for this function:

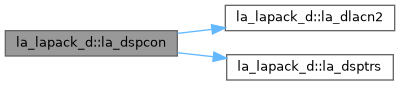
la_dspev()

subroutine, public la_lapack_d::la_dspev	(	character, intent(in)	jobz,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	ap,
		real(dp), dimension(*), intent(out)	w,
		real(dp), dimension(ldz,*), intent(out)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DSPEV: computes all the eigenvalues and, optionally, eigenvectors of a real symmetric matrix A in packed storage.

Here is the call graph for this function:

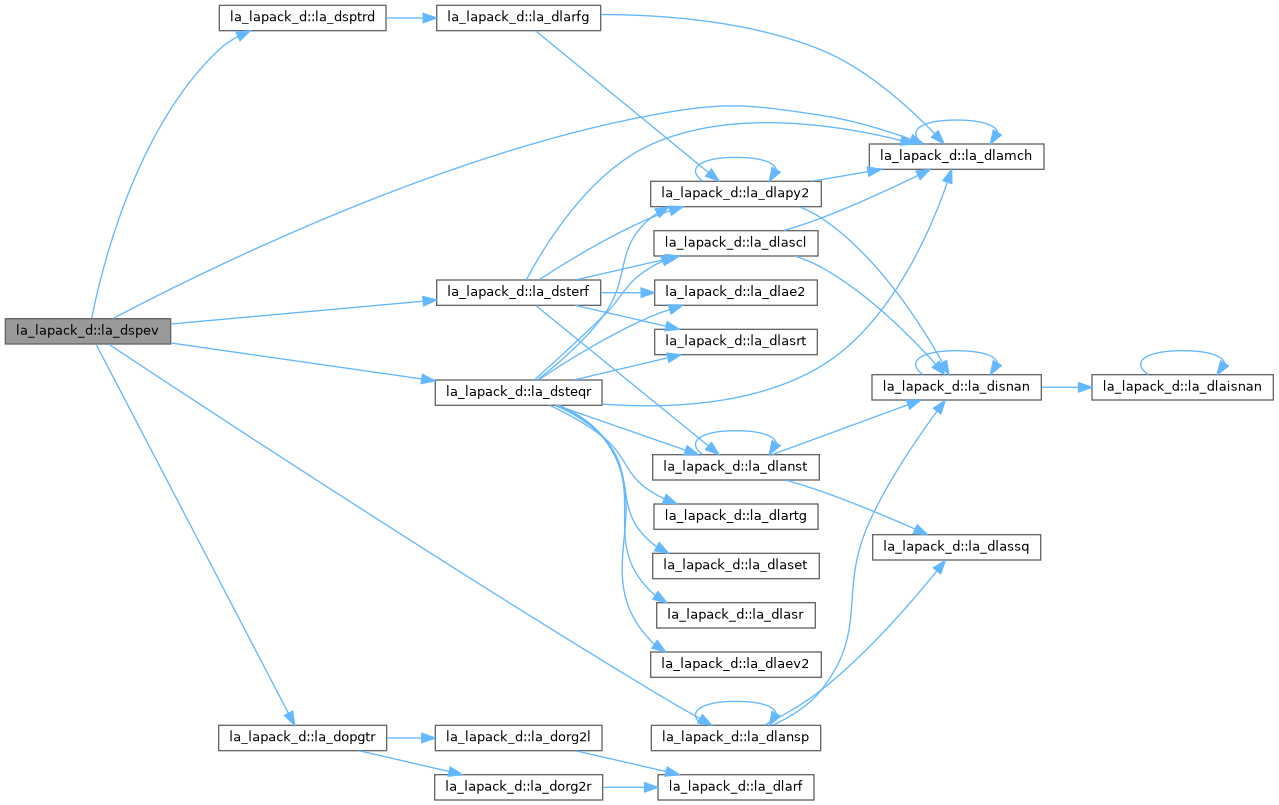
la_dspevd()

subroutine, public la_lapack_d::la_dspevd	(	character, intent(in)	jobz,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	ap,
		real(dp), dimension(*), intent(out)	w,
		real(dp), dimension(ldz,*), intent(out)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(in)	liwork,
		integer(ilp), intent(out)	info
	)

DSPEVD: computes all the eigenvalues and, optionally, eigenvectors of a real symmetric matrix A in packed storage. If eigenvectors are desired, it uses a divide and conquer algorithm. The divide and conquer algorithm makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none.

Here is the call graph for this function:

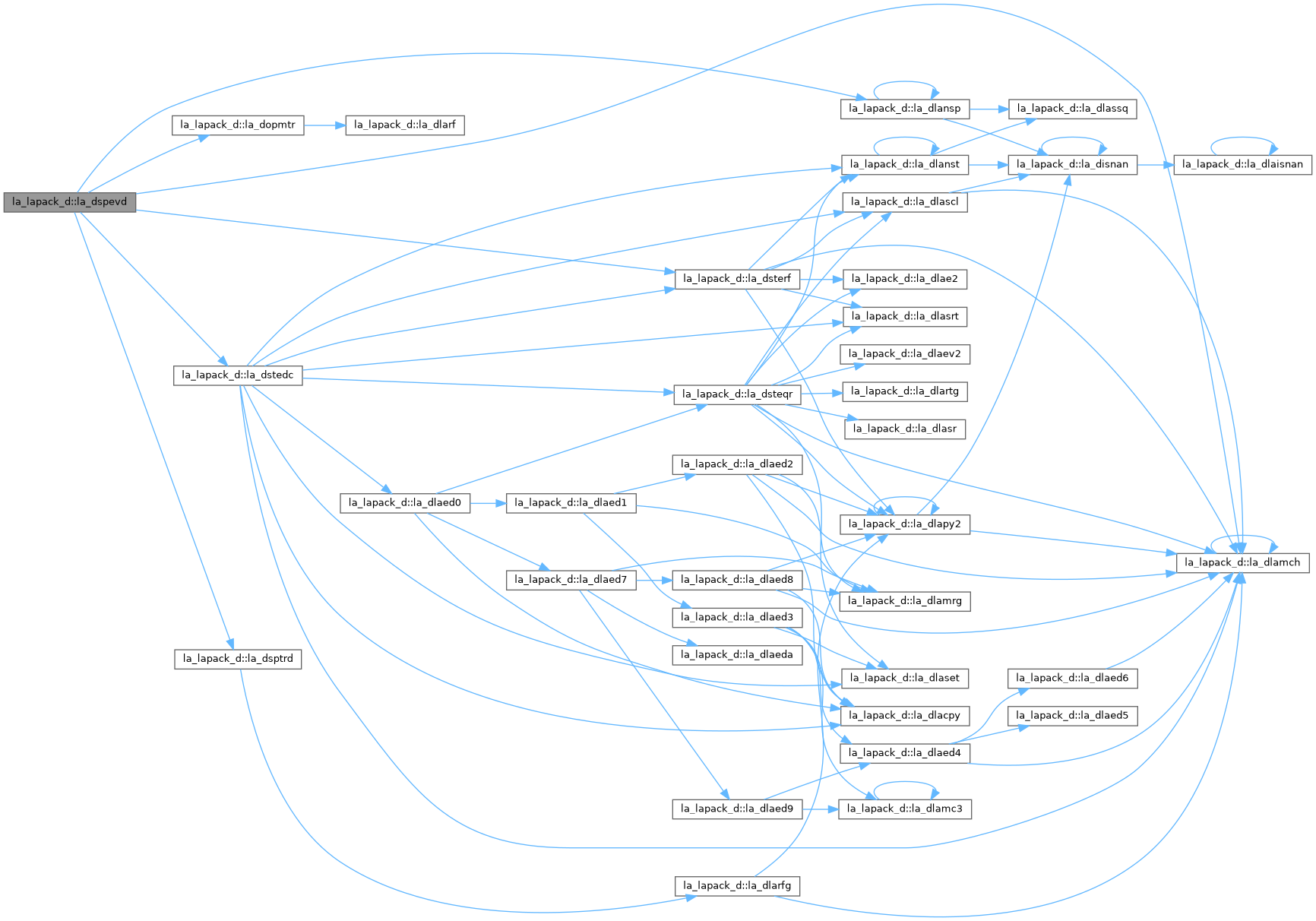
la_dspevx()

subroutine, public la_lapack_d::la_dspevx	(	character, intent(in)	jobz,
		character, intent(in)	range,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	ap,
		real(dp), intent(in)	vl,
		real(dp), intent(in)	vu,
		integer(ilp), intent(in)	il,
		integer(ilp), intent(in)	iu,
		real(dp), intent(in)	abstol,
		integer(ilp), intent(out)	m,
		real(dp), dimension(*), intent(out)	w,
		real(dp), dimension(ldz,*), intent(out)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), dimension(*), intent(out)	ifail,
		integer(ilp), intent(out)	info
	)

DSPEVX: computes selected eigenvalues and, optionally, eigenvectors of a real symmetric matrix A in packed storage. Eigenvalues/vectors can be selected by specifying either a range of values or a range of indices for the desired eigenvalues.

Here is the call graph for this function:

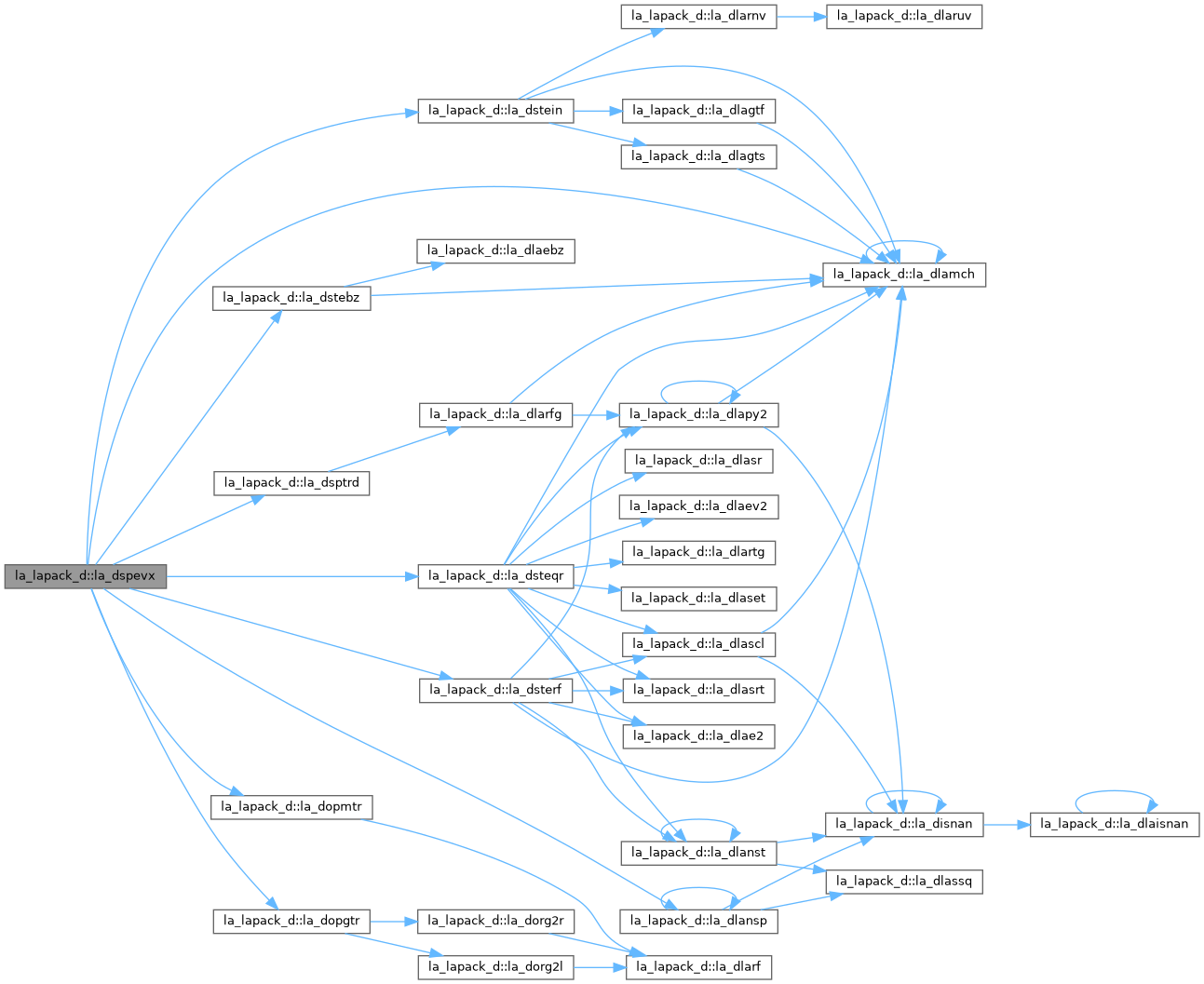
la_dspgst()

pure subroutine, public la_lapack_d::la_dspgst	(	integer(ilp), intent(in)	itype,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	ap,
		real(dp), dimension(*), intent(in)	bp,
		integer(ilp), intent(out)	info
	)

DSPGST: reduces a real symmetric-definite generalized eigenproblem to standard form, using packed storage. If ITYPE = 1, the problem is A*x = lambda*B*x, and A is overwritten by inv(U**T)*A*inv(U) or inv(L)*A*inv(L**T) If ITYPE = 2 or 3, the problem is A*B*x = lambda*x or B*A*x = lambda*x, and A is overwritten by U*A*U**T or L**T*A*L. B must have been previously factorized as U**T*U or L*L**T by DPPTRF.

la_dspgv()

subroutine, public la_lapack_d::la_dspgv	(	integer(ilp), intent(in)	itype,
		character, intent(in)	jobz,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	ap,
		real(dp), dimension(*), intent(inout)	bp,
		real(dp), dimension(*), intent(out)	w,
		real(dp), dimension(ldz,*), intent(out)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DSPGV: computes all the eigenvalues and, optionally, the eigenvectors of a real generalized symmetric-definite eigenproblem, of the form A*x=(lambda)*B*x, A*Bx=(lambda)*x, or B*A*x=(lambda)*x. Here A and B are assumed to be symmetric, stored in packed format, and B is also positive definite.

Here is the call graph for this function:

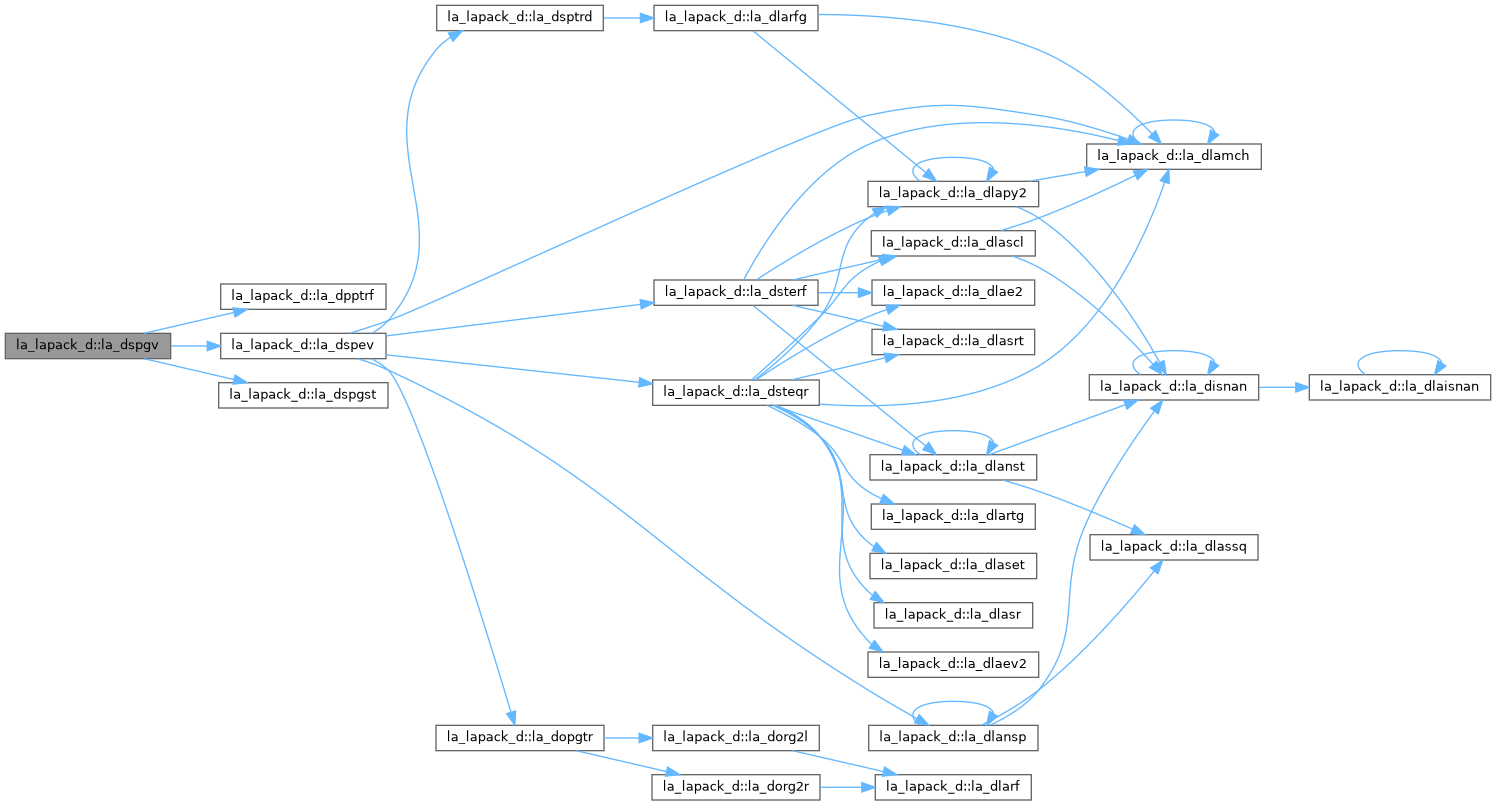
la_dspgvd()

subroutine, public la_lapack_d::la_dspgvd	(	integer(ilp), intent(in)	itype,
		character, intent(in)	jobz,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	ap,
		real(dp), dimension(*), intent(inout)	bp,
		real(dp), dimension(*), intent(out)	w,
		real(dp), dimension(ldz,*), intent(out)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(in)	liwork,
		integer(ilp), intent(out)	info
	)

DSPGVD: computes all the eigenvalues, and optionally, the eigenvectors of a real generalized symmetric-definite eigenproblem, of the form A*x=(lambda)*B*x, A*Bx=(lambda)*x, or B*A*x=(lambda)*x. Here A and B are assumed to be symmetric, stored in packed format, and B is also positive definite. If eigenvectors are desired, it uses a divide and conquer algorithm. The divide and conquer algorithm makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none.

Here is the call graph for this function:

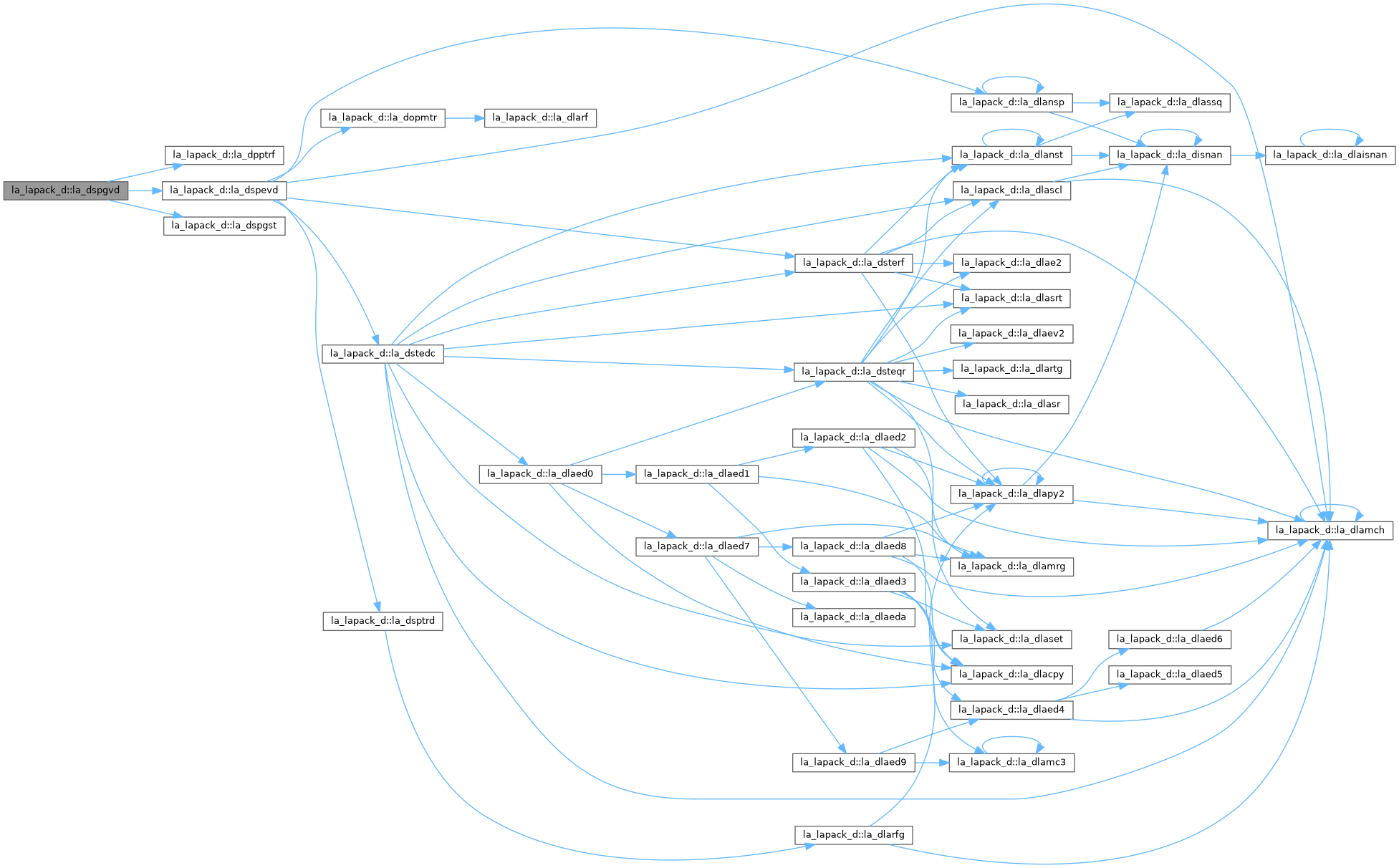
la_dspgvx()

subroutine, public la_lapack_d::la_dspgvx	(	integer(ilp), intent(in)	itype,
		character, intent(in)	jobz,
		character, intent(in)	range,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	ap,
		real(dp), dimension(*), intent(inout)	bp,
		real(dp), intent(in)	vl,
		real(dp), intent(in)	vu,
		integer(ilp), intent(in)	il,
		integer(ilp), intent(in)	iu,
		real(dp), intent(in)	abstol,
		integer(ilp), intent(out)	m,
		real(dp), dimension(*), intent(out)	w,
		real(dp), dimension(ldz,*), intent(out)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), dimension(*), intent(out)	ifail,
		integer(ilp), intent(out)	info
	)

DSPGVX: computes selected eigenvalues, and optionally, eigenvectors of a real generalized symmetric-definite eigenproblem, of the form A*x=(lambda)*B*x, A*Bx=(lambda)*x, or B*A*x=(lambda)*x. Here A and B are assumed to be symmetric, stored in packed storage, and B is also positive definite. Eigenvalues and eigenvectors can be selected by specifying either a range of values or a range of indices for the desired eigenvalues.

Here is the call graph for this function:

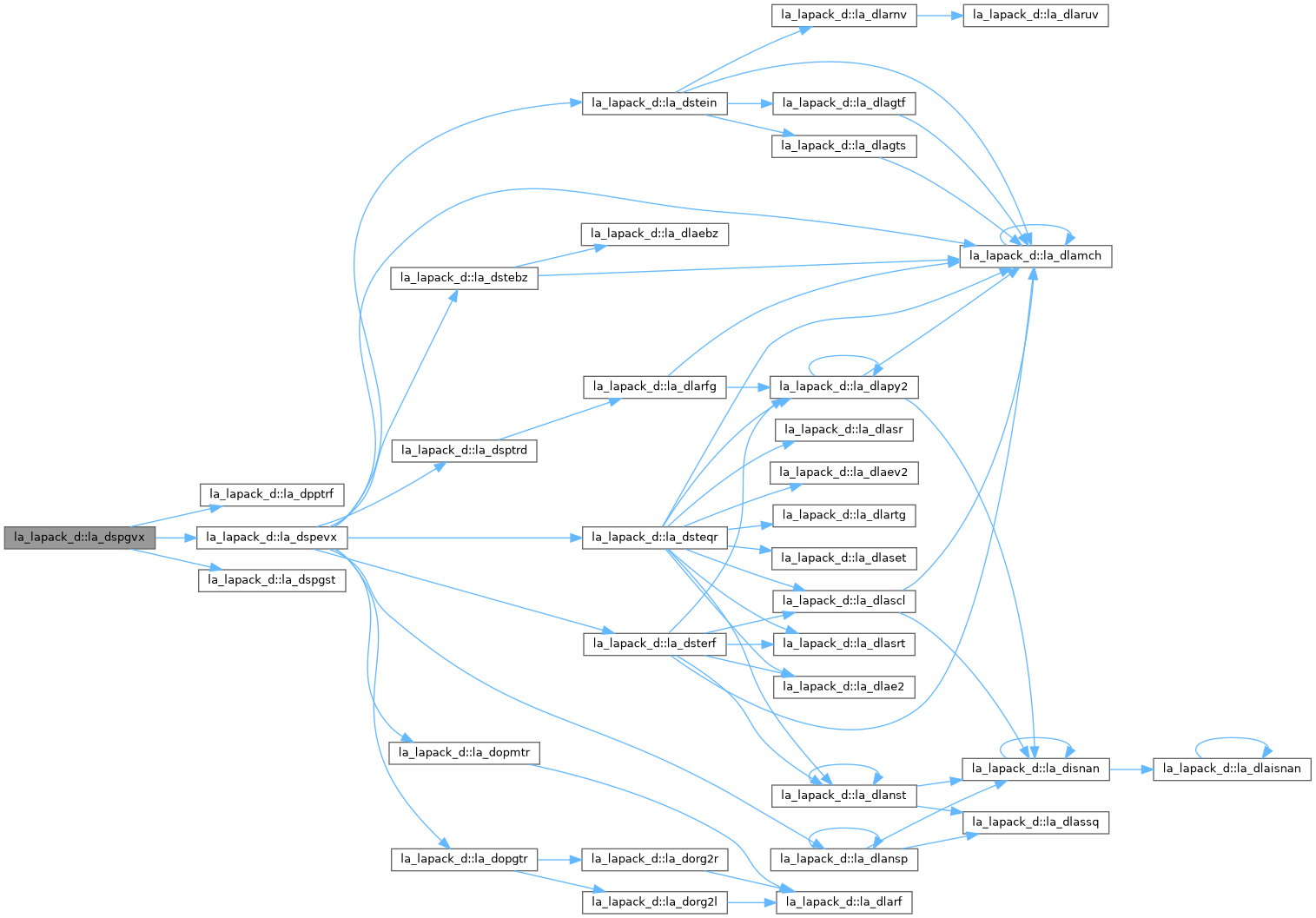
la_dsposv()

subroutine, public la_lapack_d::la_dsposv	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldx,*), intent(out)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), dimension(n,*), intent(out)	work,
		real(sp), dimension(*), intent(out)	swork,
		integer(ilp), intent(out)	iter,
		integer(ilp), intent(out)	info
	)

DSPOSV: computes the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric positive definite matrix and X and B are N-by-NRHS matrices. DSPOSV first attempts to factorize the matrix in SINGLE PRECISION and use this factorization within an iterative refinement procedure to produce a solution with DOUBLE PRECISION normwise backward error quality (see below). If the approach fails the method switches to a DOUBLE PRECISION factorization and solve. The iterative refinement is not going to be a winning strategy if the ratio SINGLE PRECISION performance over DOUBLE PRECISION performance is too small. A reasonable strategy should take the number of right-hand sides and the size of the matrix into account. This might be done with a call to ILAENV in the future. Up to now, we always try iterative refinement. The iterative refinement process is stopped if ITER > ITERMAX or for all the RHS we have: RNRM < SQRT(N)*XNRM*ANRM*EPS*BWDMAX where o ITER is the number of the current iteration in the iterative refinement process o RNRM is the infinity-norm of the residual o XNRM is the infinity-norm of the solution o ANRM is the infinity-operator-norm of the matrix A o EPS is the machine epsilon returned by DLAMCH('Epsilon') The value ITERMAX and BWDMAX are fixed to 30 and 1.0D+00 respectively.

Here is the call graph for this function:

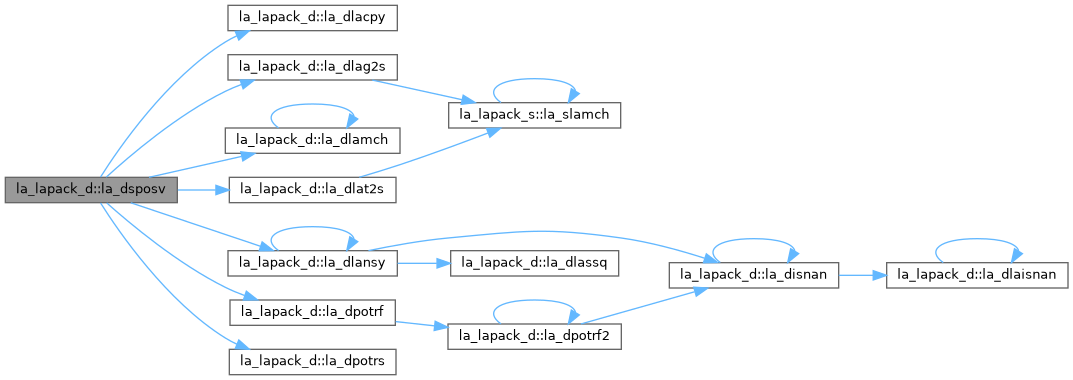
la_dsprfs()

pure subroutine, public la_lapack_d::la_dsprfs	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(*), intent(in)	ap,
		real(dp), dimension(*), intent(in)	afp,
		integer(ilp), dimension(*), intent(in)	ipiv,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldx,*), intent(inout)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), dimension(*), intent(out)	ferr,
		real(dp), dimension(*), intent(out)	berr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DSPRFS: improves the computed solution to a system of linear equations when the coefficient matrix is symmetric indefinite and packed, and provides error bounds and backward error estimates for the solution.

Here is the call graph for this function:

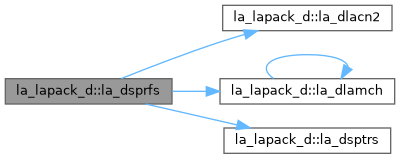
la_dspsv()

pure subroutine, public la_lapack_d::la_dspsv	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(*), intent(inout)	ap,
		integer(ilp), dimension(*), intent(out)	ipiv,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	info
	)

DSPSV: computes the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric matrix stored in packed format and X and B are N-by-NRHS matrices. The diagonal pivoting method is used to factor A as A = U * D * U**T, if UPLO = 'U', or A = L * D * L**T, if UPLO = 'L', where U (or L) is a product of permutation and unit upper (lower) triangular matrices, D is symmetric and block diagonal with 1-by-1 and 2-by-2 diagonal blocks. The factored form of A is then used to solve the system of equations A * X = B.

Here is the call graph for this function:

la_dspsvx()

subroutine, public la_lapack_d::la_dspsvx	(	character, intent(in)	fact,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(*), intent(in)	ap,
		real(dp), dimension(*), intent(inout)	afp,
		integer(ilp), dimension(*), intent(inout)	ipiv,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldx,*), intent(out)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), intent(out)	rcond,
		real(dp), dimension(*), intent(out)	ferr,
		real(dp), dimension(*), intent(out)	berr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DSPSVX: uses the diagonal pivoting factorization A = U*D*U**T or A = L*D*L**T to compute the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric matrix stored in packed format and X and B are N-by-NRHS matrices. Error bounds on the solution and a condition estimate are also provided.

Here is the call graph for this function:

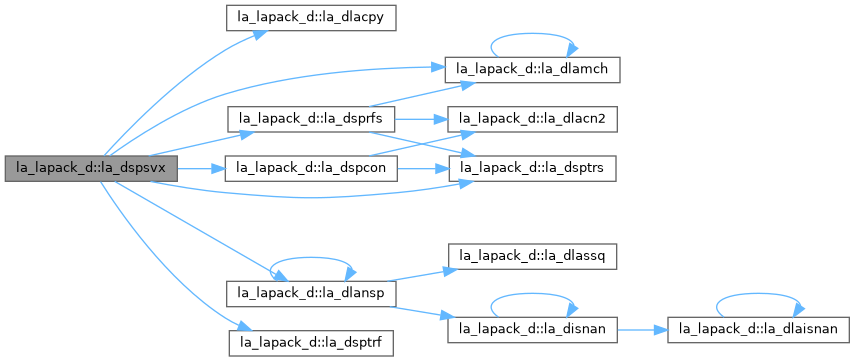
la_dsptrd()

pure subroutine, public la_lapack_d::la_dsptrd	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	ap,
		real(dp), dimension(*), intent(out)	d,
		real(dp), dimension(*), intent(out)	e,
		real(dp), dimension(*), intent(out)	tau,
		integer(ilp), intent(out)	info
	)

DSPTRD: reduces a real symmetric matrix A stored in packed form to symmetric tridiagonal form T by an orthogonal similarity transformation: Q**T * A * Q = T.

Here is the call graph for this function:

la_dsptrf()

pure subroutine, public la_lapack_d::la_dsptrf	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	ap,
		integer(ilp), dimension(*), intent(out)	ipiv,
		integer(ilp), intent(out)	info
	)

DSPTRF: computes the factorization of a real symmetric matrix A stored in packed format using the Bunch-Kaufman diagonal pivoting method: A = U*D*U**T or A = L*D*L**T where U (or L) is a product of permutation and unit upper (lower) triangular matrices, and D is symmetric and block diagonal with 1-by-1 and 2-by-2 diagonal blocks.

la_dsptri()

pure subroutine, public la_lapack_d::la_dsptri	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	ap,
		integer(ilp), dimension(*), intent(in)	ipiv,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DSPTRI: computes the inverse of a real symmetric indefinite matrix A in packed storage using the factorization A = U*D*U**T or A = L*D*L**T computed by DSPTRF.

la_dsptrs()

pure subroutine, public la_lapack_d::la_dsptrs	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(*), intent(in)	ap,
		integer(ilp), dimension(*), intent(in)	ipiv,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	info
	)

DSPTRS: solves a system of linear equations A*X = B with a real symmetric matrix A stored in packed format using the factorization A = U*D*U**T or A = L*D*L**T computed by DSPTRF.

la_dstebz()

pure subroutine, public la_lapack_d::la_dstebz	(	character, intent(in)	range,
		character, intent(in)	order,
		integer(ilp), intent(in)	n,
		real(dp), intent(in)	vl,
		real(dp), intent(in)	vu,
		integer(ilp), intent(in)	il,
		integer(ilp), intent(in)	iu,
		real(dp), intent(in)	abstol,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(in)	e,
		integer(ilp), intent(out)	m,
		integer(ilp), intent(out)	nsplit,
		real(dp), dimension(*), intent(out)	w,
		integer(ilp), dimension(*), intent(out)	iblock,
		integer(ilp), dimension(*), intent(out)	isplit,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DSTEBZ: computes the eigenvalues of a symmetric tridiagonal matrix T. The user may ask for all eigenvalues, all eigenvalues in the half-open interval (VL, VU], or the IL-th through IU-th eigenvalues. To avoid overflow, the matrix must be scaled so that its largest element is no greater than overflow**(1/2) * underflow**(1/4) in absolute value, and for greatest accuracy, it should not be much smaller than that. See W. Kahan "Accurate Eigenvalues of a Symmetric Tridiagonal Matrix", Report CS41, Computer Science Dept., Stanford University, July 21, 1966.

Here is the call graph for this function:

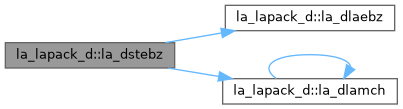
la_dstedc()

pure subroutine, public la_lapack_d::la_dstedc	(	character, intent(in)	compz,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(inout)	e,
		real(dp), dimension(ldz,*), intent(inout)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(in)	liwork,
		integer(ilp), intent(out)	info
	)

DSTEDC: computes all eigenvalues and, optionally, eigenvectors of a symmetric tridiagonal matrix using the divide and conquer method. The eigenvectors of a full or band real symmetric matrix can also be found if DSYTRD or DSPTRD or DSBTRD has been used to reduce this matrix to tridiagonal form. This code makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none. See DLAED3 for details.

Here is the call graph for this function:

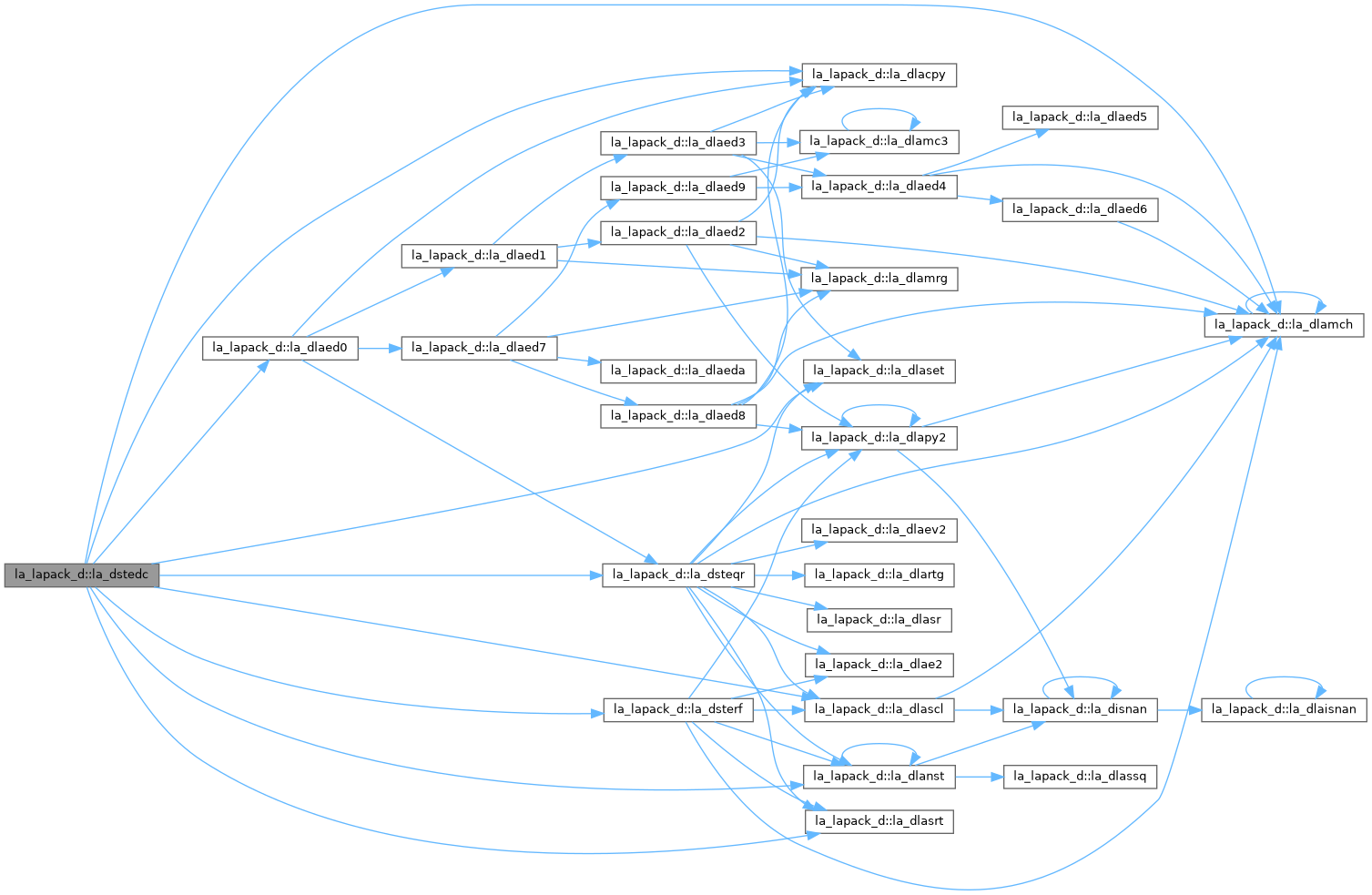
la_dstegr()

pure subroutine, public la_lapack_d::la_dstegr	(	character, intent(in)	jobz,
		character, intent(in)	range,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(inout)	e,
		real(dp), intent(in)	vl,
		real(dp), intent(in)	vu,
		integer(ilp), intent(in)	il,
		integer(ilp), intent(in)	iu,
		real(dp), intent(in)	abstol,
		integer(ilp), intent(out)	m,
		real(dp), dimension(*), intent(out)	w,
		real(dp), dimension(ldz,*), intent(out)	z,
		integer(ilp), intent(in)	ldz,
		integer(ilp), dimension(*), intent(out)	isuppz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(in)	liwork,
		integer(ilp), intent(out)	info
	)

DSTEGR: computes selected eigenvalues and, optionally, eigenvectors of a real symmetric tridiagonal matrix T. Any such unreduced matrix has a well defined set of pairwise different real eigenvalues, the corresponding real eigenvectors are pairwise orthogonal. The spectrum may be computed either completely or partially by specifying either an interval (VL,VU] or a range of indices IL:IU for the desired eigenvalues. DSTEGR is a compatibility wrapper around the improved DSTEMR routine. See DSTEMR for further details. One important change is that the ABSTOL parameter no longer provides any benefit and hence is no longer used. Note : DSTEGR and DSTEMR work only on machines which follow IEEE-754 floating-point standard in their handling of infinities and NaNs. Normal execution may create these exceptiona values and hence may abort due to a floating point exception in environments which do not conform to the IEEE-754 standard.

Here is the call graph for this function:

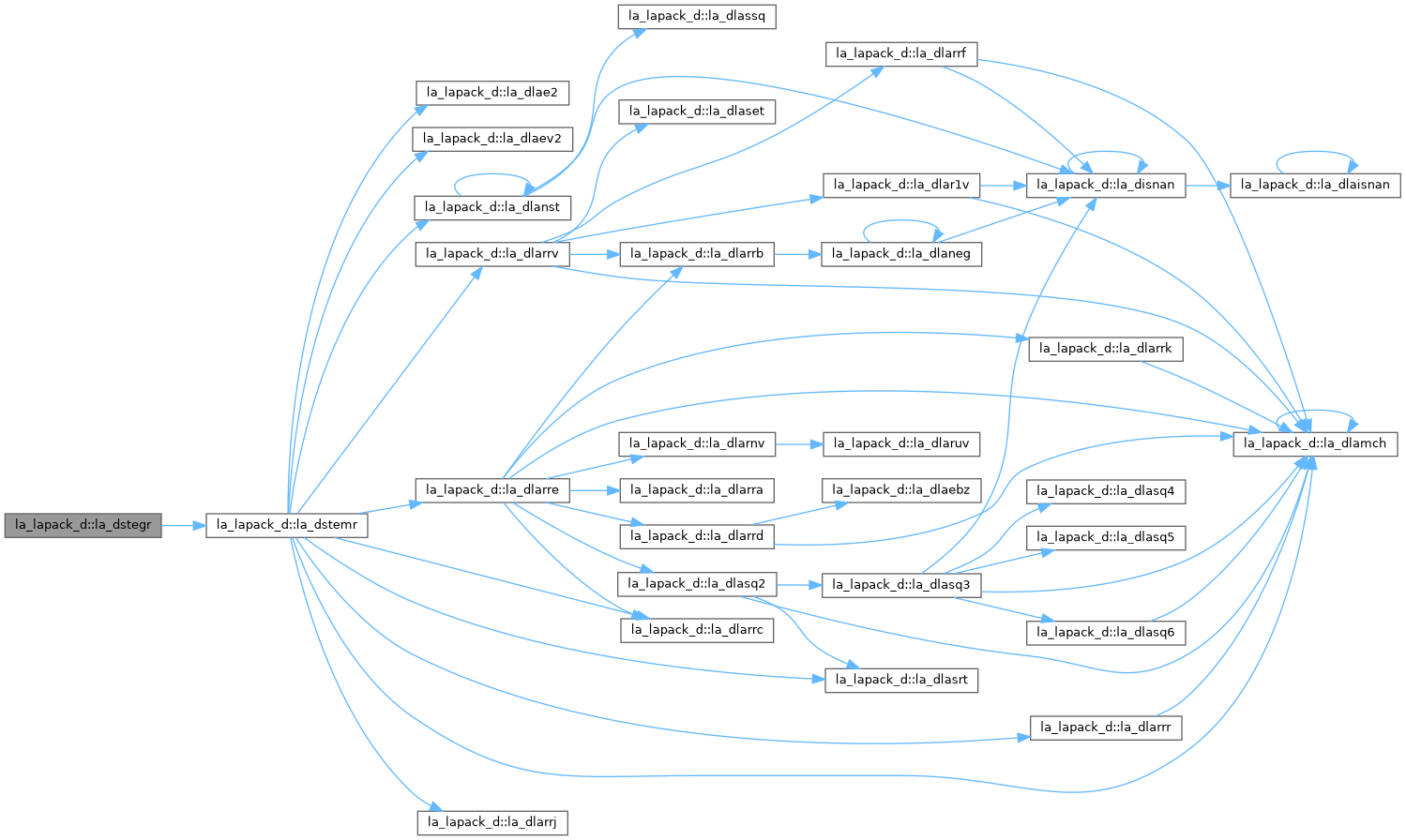
la_dstein()

pure subroutine, public la_lapack_d::la_dstein	(	integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(in)	d,
		real(dp), dimension(*), intent(in)	e,
		integer(ilp), intent(in)	m,
		real(dp), dimension(*), intent(in)	w,
		integer(ilp), dimension(*), intent(in)	iblock,
		integer(ilp), dimension(*), intent(in)	isplit,
		real(dp), dimension(ldz,*), intent(out)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), dimension(*), intent(out)	ifail,
		integer(ilp), intent(out)	info
	)

DSTEIN: computes the eigenvectors of a real symmetric tridiagonal matrix T corresponding to specified eigenvalues, using inverse iteration. The maximum number of iterations allowed for each eigenvector is specified by an internal parameter MAXITS (currently set to 5).

Here is the call graph for this function:

la_dstemr()

pure subroutine, public la_lapack_d::la_dstemr	(	character, intent(in)	jobz,
		character, intent(in)	range,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(inout)	e,
		real(dp), intent(in)	vl,
		real(dp), intent(in)	vu,
		integer(ilp), intent(in)	il,
		integer(ilp), intent(in)	iu,
		integer(ilp), intent(out)	m,
		real(dp), dimension(*), intent(out)	w,
		real(dp), dimension(ldz,*), intent(out)	z,
		integer(ilp), intent(in)	ldz,
		integer(ilp), intent(in)	nzc,
		integer(ilp), dimension(*), intent(out)	isuppz,
		logical(lk), intent(inout)	tryrac,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(in)	liwork,
		integer(ilp), intent(out)	info
	)

DSTEMR: computes selected eigenvalues and, optionally, eigenvectors of a real symmetric tridiagonal matrix T. Any such unreduced matrix has a well defined set of pairwise different real eigenvalues, the corresponding real eigenvectors are pairwise orthogonal. The spectrum may be computed either completely or partially by specifying either an interval (VL,VU] or a range of indices IL:IU for the desired eigenvalues. Depending on the number of desired eigenvalues, these are computed either by bisection or the dqds algorithm. Numerically orthogonal eigenvectors are computed by the use of various suitable L D L^T factorizations near clusters of close eigenvalues (referred to as RRRs, Relatively Robust Representations). An informal sketch of the algorithm follows. For each unreduced block (submatrix) of T, (a) Compute T - sigma I = L D L^T, so that L and D define all the wanted eigenvalues to high relative accuracy. This means that small relative changes in the entries of D and L cause only small relative changes in the eigenvalues and eigenvectors. The standard (unfactored) representation of the tridiagonal matrix T does not have this property in general. (b) Compute the eigenvalues to suitable accuracy. If the eigenvectors are desired, the algorithm attains full accuracy of the computed eigenvalues only right before the corresponding vectors have to be computed, see steps c) and d). (c) For each cluster of close eigenvalues, select a new shift close to the cluster, find a new factorization, and refine the shifted eigenvalues to suitable accuracy. (d) For each eigenvalue with a large enough relative separation compute the corresponding eigenvector by forming a rank revealing twisted factorization. Go back to (c) for any clusters that remain. For more details, see:

• Inderjit S. Dhillon and Beresford N. Parlett: "Multiple representations to compute orthogonal eigenvectors of symmetric tridiagonal matrices," Linear Algebra and its Applications, 387(1), pp. 1-28, August 2004.
• Inderjit Dhillon and Beresford Parlett: "Orthogonal Eigenvectors and Relative Gaps," SIAM Journal on Matrix Analysis and Applications, Vol. 25,

1. Also LAPACK Working Note 154.

• Inderjit Dhillon: "A new O(n^2) algorithm for the symmetric tridiagonal eigenvalue/eigenvector problem", Computer Science Division Technical Report No. UCB/CSD-97-971, UC Berkeley, May 1997. Further Details 1.DSTEMR works only on machines which follow IEEE-754 floating-point standard in their handling of infinities and NaNs. This permits the use of efficient inner loops avoiding a check for zero divisors.

Here is the call graph for this function:

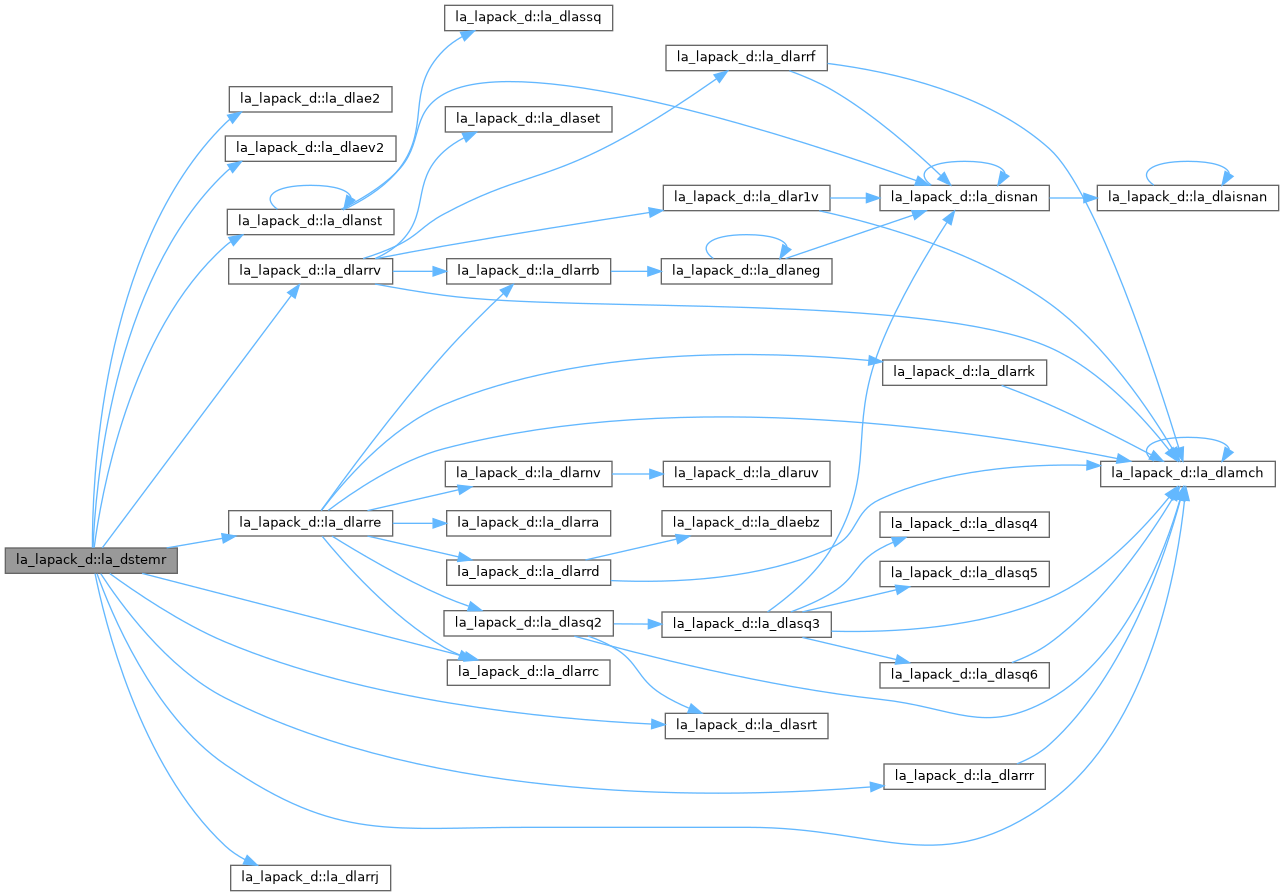
la_dsteqr()

pure subroutine, public la_lapack_d::la_dsteqr	(	character, intent(in)	compz,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(inout)	e,
		real(dp), dimension(ldz,*), intent(inout)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DSTEQR: computes all eigenvalues and, optionally, eigenvectors of a symmetric tridiagonal matrix using the implicit QL or QR method. The eigenvectors of a full or band symmetric matrix can also be found if DSYTRD or DSPTRD or DSBTRD has been used to reduce this matrix to tridiagonal form.

Here is the call graph for this function:

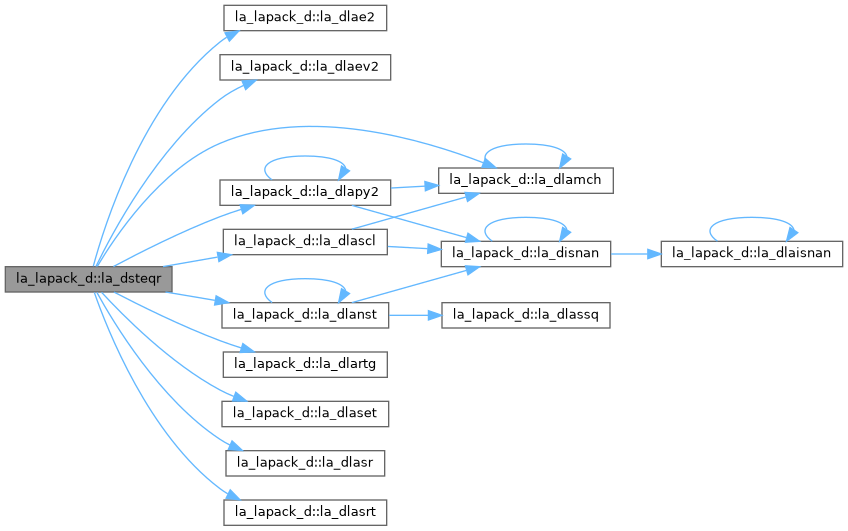
la_dsterf()

pure subroutine, public la_lapack_d::la_dsterf	(	integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(inout)	e,
		integer(ilp), intent(out)	info
	)

DSTERF: computes all eigenvalues of a symmetric tridiagonal matrix using the Pal-Walker-Kahan variant of the QL or QR algorithm.

Here is the call graph for this function:

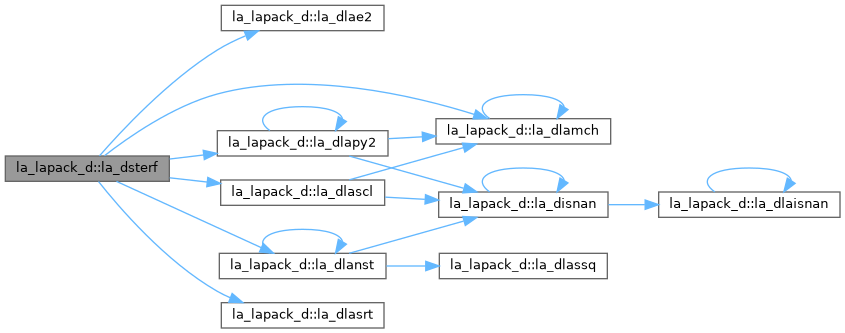
la_dstev()

pure subroutine, public la_lapack_d::la_dstev	(	character, intent(in)	jobz,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(inout)	e,
		real(dp), dimension(ldz,*), intent(out)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DSTEV: computes all eigenvalues and, optionally, eigenvectors of a real symmetric tridiagonal matrix A.

Here is the call graph for this function:

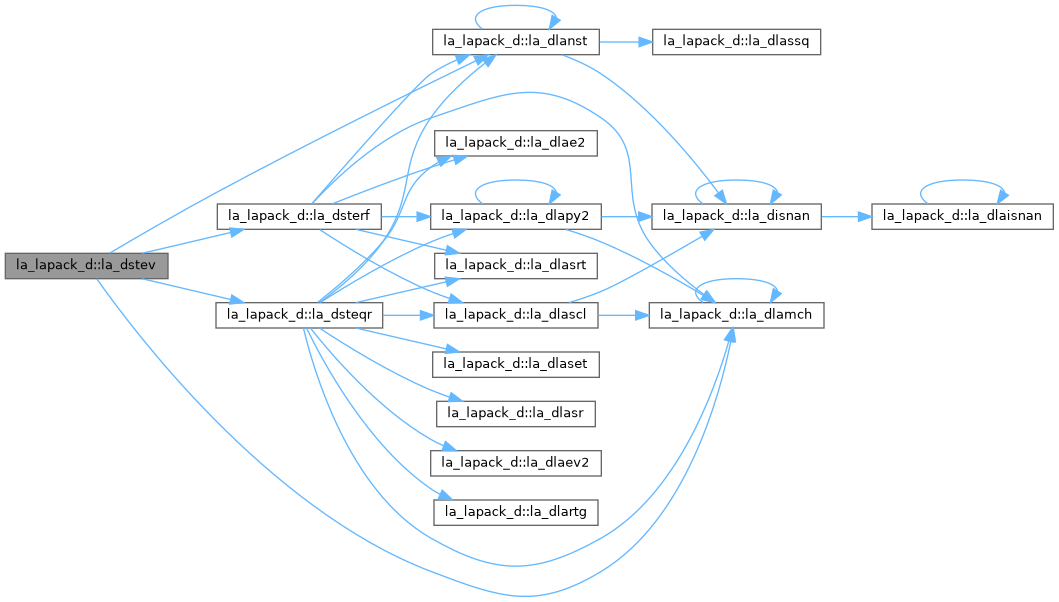
la_dstevd()

pure subroutine, public la_lapack_d::la_dstevd	(	character, intent(in)	jobz,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(inout)	e,
		real(dp), dimension(ldz,*), intent(out)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(in)	liwork,
		integer(ilp), intent(out)	info
	)

DSTEVD: computes all eigenvalues and, optionally, eigenvectors of a real symmetric tridiagonal matrix. If eigenvectors are desired, it uses a divide and conquer algorithm. The divide and conquer algorithm makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none.

Here is the call graph for this function:

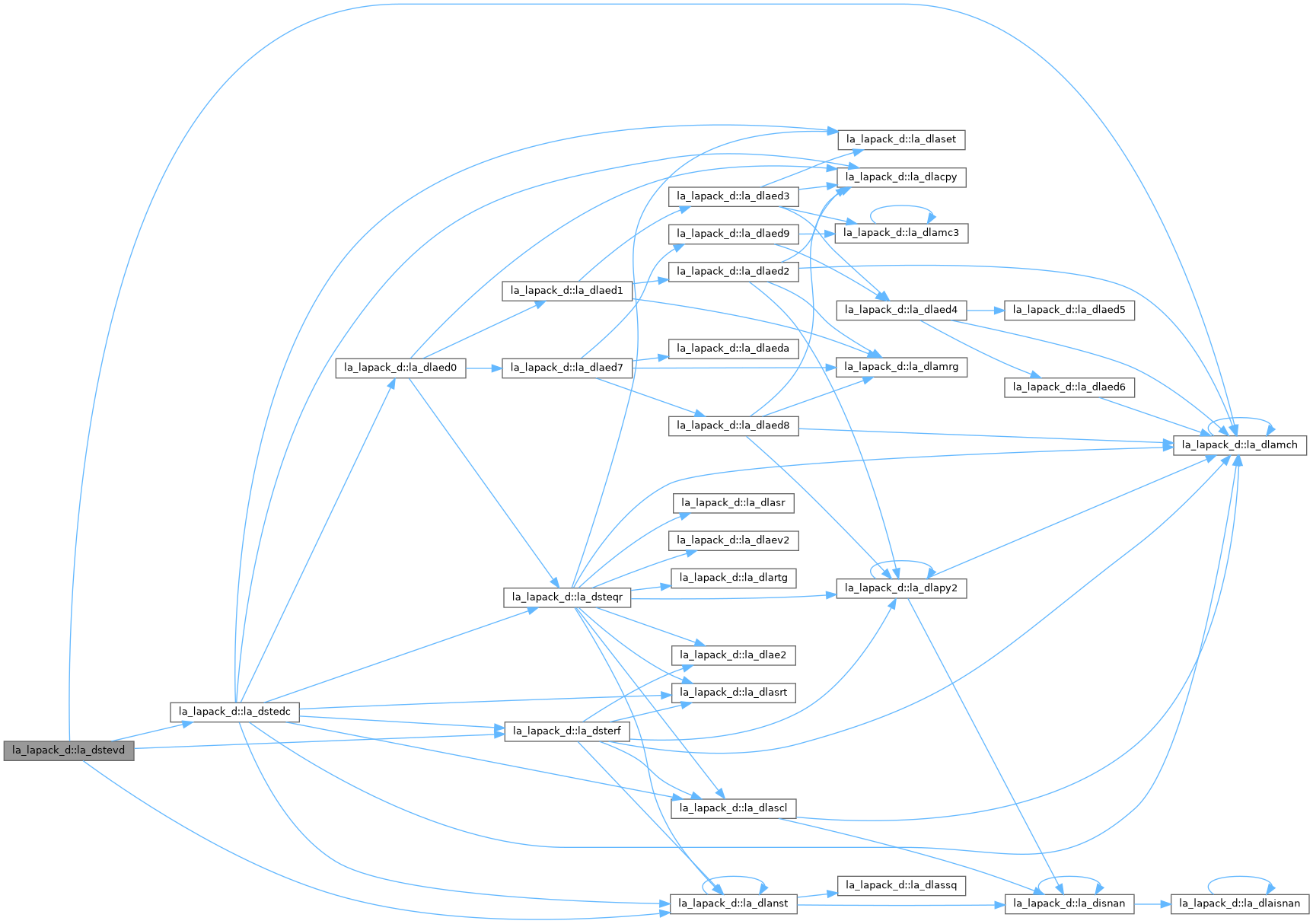
la_dstevr()

pure subroutine, public la_lapack_d::la_dstevr	(	character, intent(in)	jobz,
		character, intent(in)	range,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(inout)	e,
		real(dp), intent(in)	vl,
		real(dp), intent(in)	vu,
		integer(ilp), intent(in)	il,
		integer(ilp), intent(in)	iu,
		real(dp), intent(in)	abstol,
		integer(ilp), intent(out)	m,
		real(dp), dimension(*), intent(out)	w,
		real(dp), dimension(ldz,*), intent(out)	z,
		integer(ilp), intent(in)	ldz,
		integer(ilp), dimension(*), intent(out)	isuppz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(in)	liwork,
		integer(ilp), intent(out)	info
	)

DSTEVR: computes selected eigenvalues and, optionally, eigenvectors of a real symmetric tridiagonal matrix T. Eigenvalues and eigenvectors can be selected by specifying either a range of values or a range of indices for the desired eigenvalues. Whenever possible, DSTEVR calls DSTEMR to compute the eigenspectrum using Relatively Robust Representations. DSTEMR computes eigenvalues by the dqds algorithm, while orthogonal eigenvectors are computed from various "good" L D L^T representations (also known as Relatively Robust Representations). Gram-Schmidt orthogonalization is avoided as far as possible. More specifically, the various steps of the algorithm are as follows. For the i-th unreduced block of T, (a) Compute T - sigma_i = L_i D_i L_i^T, such that L_i D_i L_i^T is a relatively robust representation, (b) Compute the eigenvalues, lambda_j, of L_i D_i L_i^T to high relative accuracy by the dqds algorithm, (c) If there is a cluster of close eigenvalues, "choose" sigma_i close to the cluster, and go to step (a), (d) Given the approximate eigenvalue lambda_j of L_i D_i L_i^T, compute the corresponding eigenvector by forming a rank-revealing twisted factorization. The desired accuracy of the output can be specified by the input parameter ABSTOL. For more details, see "A new O(n^2) algorithm for the symmetric tridiagonal eigenvalue/eigenvector problem", by Inderjit Dhillon, Computer Science Division Technical Report No. UCB//CSD-97-971, UC Berkeley, May 1997. Note 1 : DSTEVR calls DSTEMR when the full spectrum is requested on machines which conform to the ieee-754 floating point standard. DSTEVR calls DSTEBZ and DSTEIN on non-ieee machines and when partial spectrum requests are made. Normal execution of DSTEMR may create NaNs and infinities and hence may abort due to a floating point exception in environments which do not handle NaNs and infinities in the ieee standard default manner.

Here is the call graph for this function:

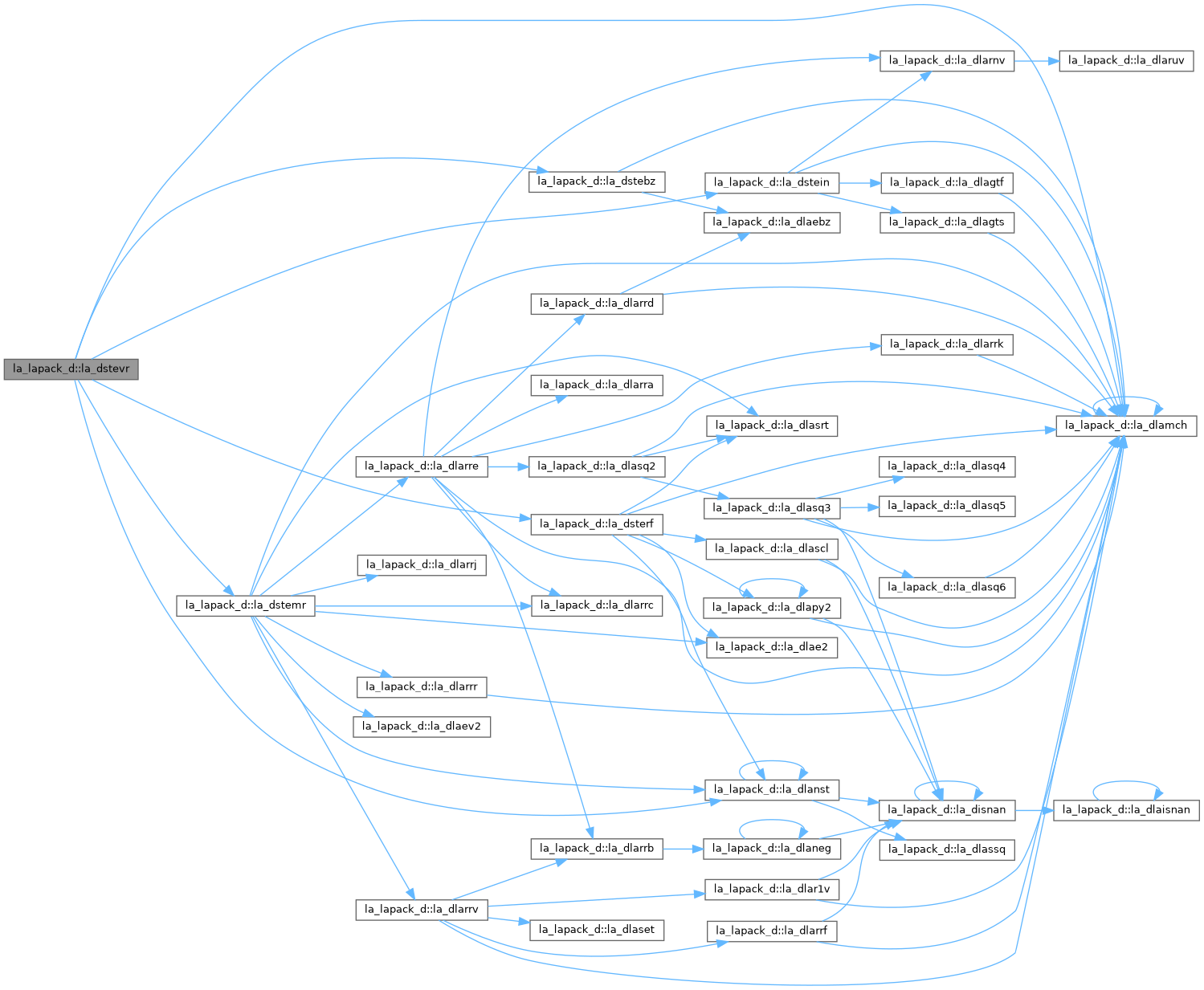
la_dstevx()

pure subroutine, public la_lapack_d::la_dstevx	(	character, intent(in)	jobz,
		character, intent(in)	range,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(inout)	e,
		real(dp), intent(in)	vl,
		real(dp), intent(in)	vu,
		integer(ilp), intent(in)	il,
		integer(ilp), intent(in)	iu,
		real(dp), intent(in)	abstol,
		integer(ilp), intent(out)	m,
		real(dp), dimension(*), intent(out)	w,
		real(dp), dimension(ldz,*), intent(out)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), dimension(*), intent(out)	ifail,
		integer(ilp), intent(out)	info
	)

DSTEVX: computes selected eigenvalues and, optionally, eigenvectors of a real symmetric tridiagonal matrix A. Eigenvalues and eigenvectors can be selected by specifying either a range of values or a range of indices for the desired eigenvalues.

Here is the call graph for this function:

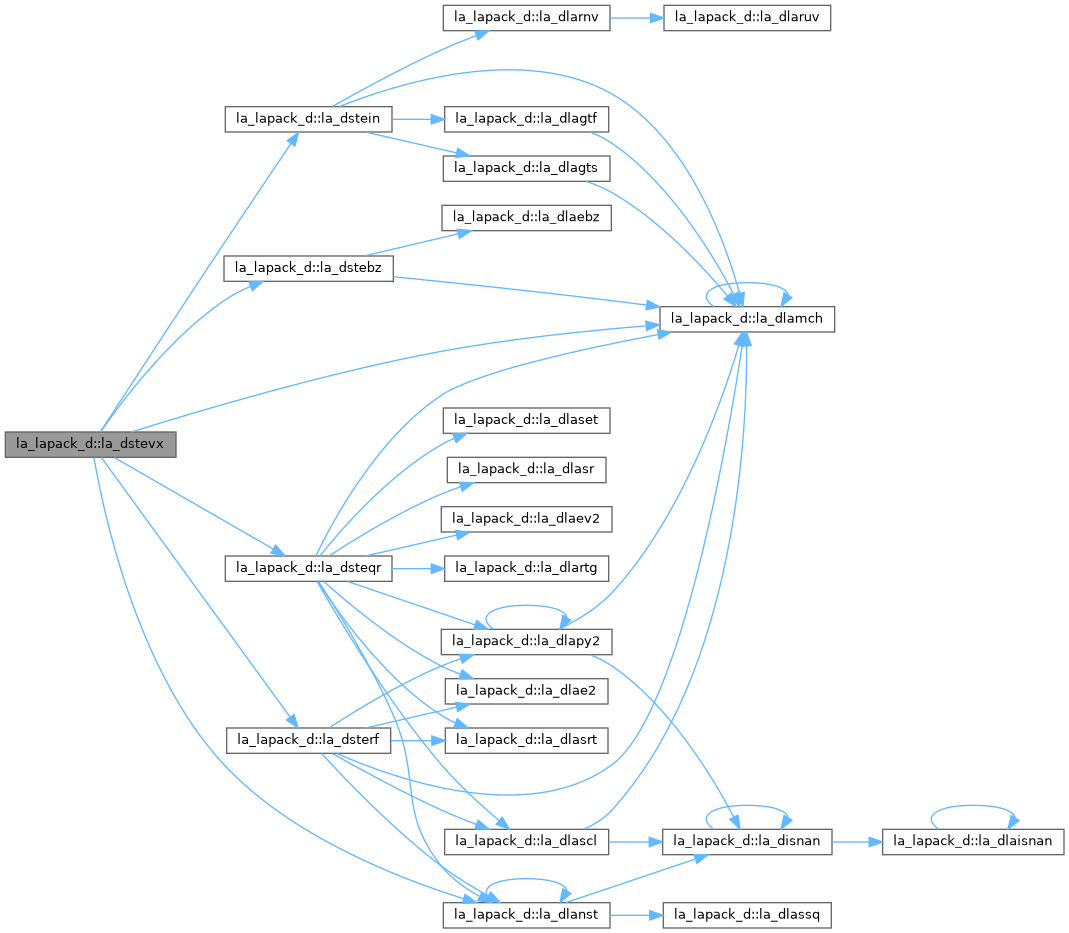
la_dsycon()

pure subroutine, public la_lapack_d::la_dsycon	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(in)	ipiv,
		real(dp), intent(in)	anorm,
		real(dp), intent(out)	rcond,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DSYCON: estimates the reciprocal of the condition number (in the 1-norm) of a real symmetric matrix A using the factorization A = U*D*U**T or A = L*D*L**T computed by DSYTRF. An estimate is obtained for norm(inv(A)), and the reciprocal of the condition number is computed as RCOND = 1 / (ANORM * norm(inv(A))).

Here is the call graph for this function:

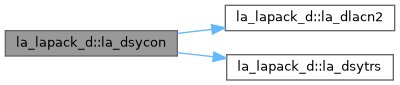
la_dsycon_rook()

pure subroutine, public la_lapack_d::la_dsycon_rook	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(in)	ipiv,
		real(dp), intent(in)	anorm,
		real(dp), intent(out)	rcond,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DSYCON_ROOK: estimates the reciprocal of the condition number (in the 1-norm) of a real symmetric matrix A using the factorization A = U*D*U**T or A = L*D*L**T computed by DSYTRF_ROOK. An estimate is obtained for norm(inv(A)), and the reciprocal of the condition number is computed as RCOND = 1 / (ANORM * norm(inv(A))).

Here is the call graph for this function:

la_dsyconv()

pure subroutine, public la_lapack_d::la_dsyconv	(	character, intent(in)	uplo,
		character, intent(in)	way,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(in)	ipiv,
		real(dp), dimension(*), intent(out)	e,
		integer(ilp), intent(out)	info
	)

DSYCONV: convert A given by TRF into L and D and vice-versa. Get Non-diag elements of D (returned in workspace) and apply or reverse permutation done in TRF.

la_dsyconvf()

pure subroutine, public la_lapack_d::la_dsyconvf	(	character, intent(in)	uplo,
		character, intent(in)	way,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(inout)	e,
		integer(ilp), dimension(*), intent(inout)	ipiv,
		integer(ilp), intent(out)	info
	)

If parameter WAY = 'C': DSYCONVF: converts the factorization output format used in DSYTRF provided on entry in parameter A into the factorization output format used in DSYTRF_RK (or DSYTRF_BK) that is stored on exit in parameters A and E. It also converts in place details of the intechanges stored in IPIV from the format used in DSYTRF into the format used in DSYTRF_RK (or DSYTRF_BK). If parameter WAY = 'R': DSYCONVF performs the conversion in reverse direction, i.e. converts the factorization output format used in DSYTRF_RK (or DSYTRF_BK) provided on entry in parameters A and E into the factorization output format used in DSYTRF that is stored on exit in parameter A. It also converts in place details of the intechanges stored in IPIV from the format used in DSYTRF_RK (or DSYTRF_BK) into the format used in DSYTRF.

la_dsyconvf_rook()

pure subroutine, public la_lapack_d::la_dsyconvf_rook	(	character, intent(in)	uplo,
		character, intent(in)	way,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(inout)	e,
		integer(ilp), dimension(*), intent(in)	ipiv,
		integer(ilp), intent(out)	info
	)

If parameter WAY = 'C': DSYCONVF_ROOK: converts the factorization output format used in DSYTRF_ROOK provided on entry in parameter A into the factorization output format used in DSYTRF_RK (or DSYTRF_BK) that is stored on exit in parameters A and E. IPIV format for DSYTRF_ROOK and DSYTRF_RK (or DSYTRF_BK) is the same and is not converted. If parameter WAY = 'R': DSYCONVF_ROOK performs the conversion in reverse direction, i.e. converts the factorization output format used in DSYTRF_RK (or DSYTRF_BK) provided on entry in parameters A and E into the factorization output format used in DSYTRF_ROOK that is stored on exit in parameter A. IPIV format for DSYTRF_ROOK and DSYTRF_RK (or DSYTRF_BK) is the same and is not converted.

la_dsyequb()

pure subroutine, public la_lapack_d::la_dsyequb	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	s,
		real(dp), intent(out)	scond,
		real(dp), intent(out)	amax,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DSYEQUB: computes row and column scalings intended to equilibrate a symmetric matrix A (with respect to the Euclidean norm) and reduce its condition number. The scale factors S are computed by the BIN algorithm (see references) so that the scaled matrix B with elements B(i,j) = S(i)*A(i,j)*S(j) has a condition number within a factor N of the smallest possible condition number over all possible diagonal scalings.

Here is the call graph for this function:

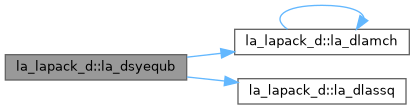
la_dsyev()

subroutine, public la_lapack_d::la_dsyev	(	character, intent(in)	jobz,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	w,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DSYEV: computes all eigenvalues and, optionally, eigenvectors of a real symmetric matrix A.

Here is the call graph for this function:

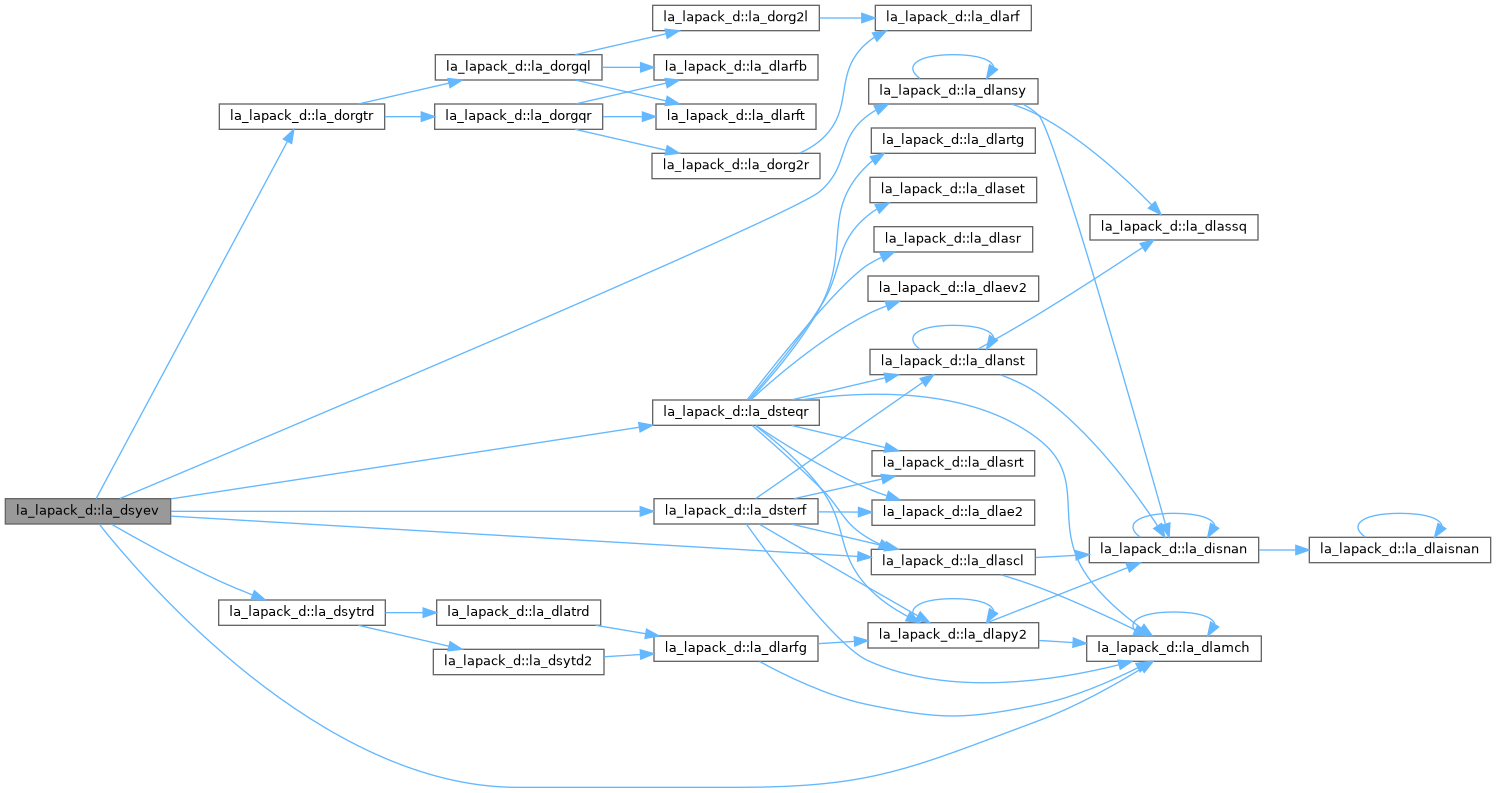
la_dsyevd()

subroutine, public la_lapack_d::la_dsyevd	(	character, intent(in)	jobz,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	w,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(in)	liwork,
		integer(ilp), intent(out)	info
	)

DSYEVD: computes all eigenvalues and, optionally, eigenvectors of a real symmetric matrix A. If eigenvectors are desired, it uses a divide and conquer algorithm. The divide and conquer algorithm makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none. Because of large use of BLAS of level 3, DSYEVD needs N**2 more workspace than DSYEVX.

Here is the call graph for this function:

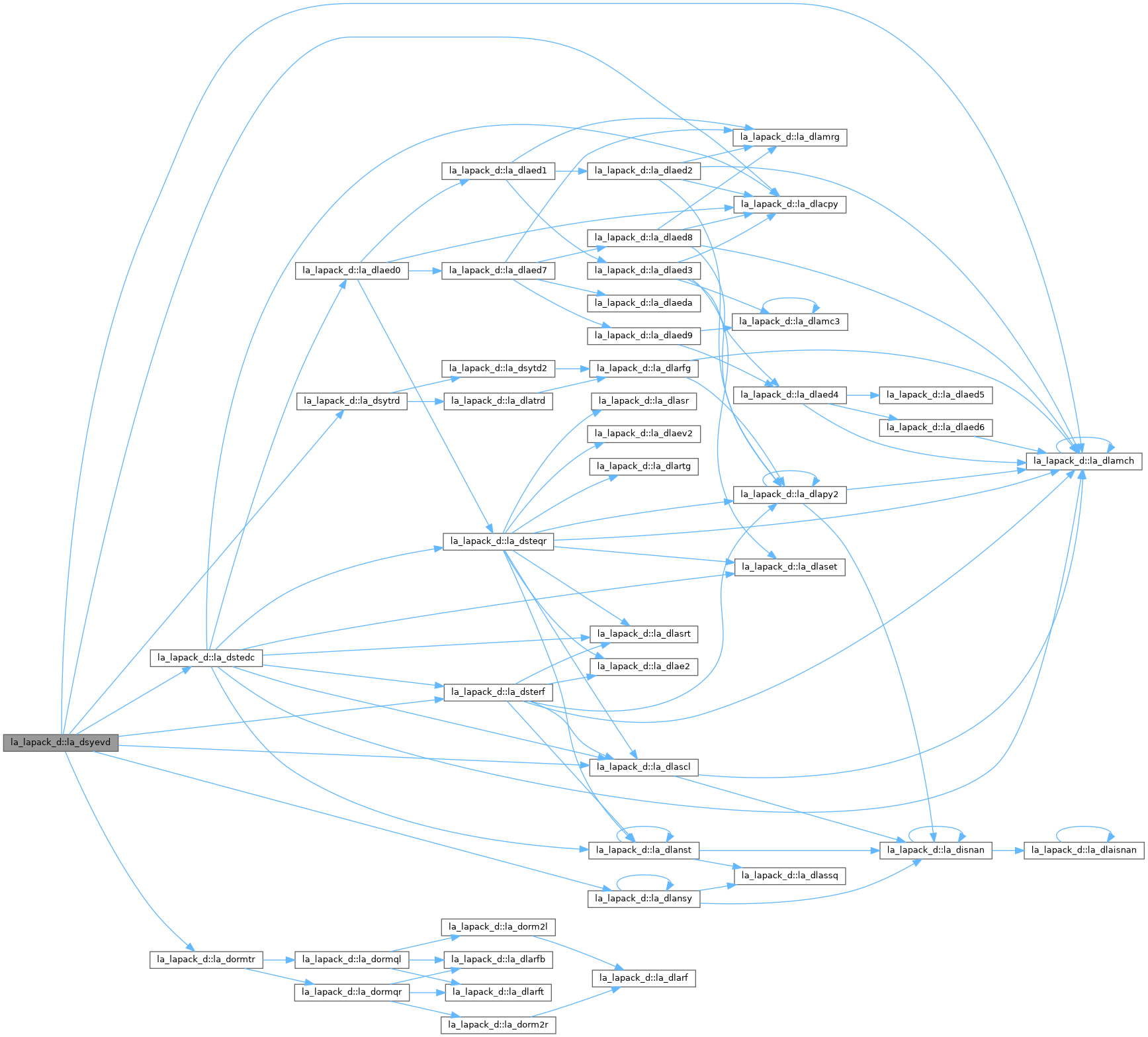
la_dsyevr()

subroutine, public la_lapack_d::la_dsyevr	(	character, intent(in)	jobz,
		character, intent(in)	range,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), intent(in)	vl,
		real(dp), intent(in)	vu,
		integer(ilp), intent(in)	il,
		integer(ilp), intent(in)	iu,
		real(dp), intent(in)	abstol,
		integer(ilp), intent(out)	m,
		real(dp), dimension(*), intent(out)	w,
		real(dp), dimension(ldz,*), intent(out)	z,
		integer(ilp), intent(in)	ldz,
		integer(ilp), dimension(*), intent(out)	isuppz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(in)	liwork,
		integer(ilp), intent(out)	info
	)

DSYEVR: computes selected eigenvalues and, optionally, eigenvectors of a real symmetric matrix A. Eigenvalues and eigenvectors can be selected by specifying either a range of values or a range of indices for the desired eigenvalues. DSYEVR first reduces the matrix A to tridiagonal form T with a call to DSYTRD. Then, whenever possible, DSYEVR calls DSTEMR to compute the eigenspectrum using Relatively Robust Representations. DSTEMR computes eigenvalues by the dqds algorithm, while orthogonal eigenvectors are computed from various "good" L D L^T representations (also known as Relatively Robust Representations). Gram-Schmidt orthogonalization is avoided as far as possible. More specifically, the various steps of the algorithm are as follows. For each unreduced block (submatrix) of T, (a) Compute T - sigma I = L D L^T, so that L and D define all the wanted eigenvalues to high relative accuracy. This means that small relative changes in the entries of D and L cause only small relative changes in the eigenvalues and eigenvectors. The standard (unfactored) representation of the tridiagonal matrix T does not have this property in general. (b) Compute the eigenvalues to suitable accuracy. If the eigenvectors are desired, the algorithm attains full accuracy of the computed eigenvalues only right before the corresponding vectors have to be computed, see steps c) and d). (c) For each cluster of close eigenvalues, select a new shift close to the cluster, find a new factorization, and refine the shifted eigenvalues to suitable accuracy. (d) For each eigenvalue with a large enough relative separation compute the corresponding eigenvector by forming a rank revealing twisted factorization. Go back to (c) for any clusters that remain. The desired accuracy of the output can be specified by the input parameter ABSTOL. For more details, see DSTEMR's documentation and:

• Inderjit S. Dhillon and Beresford N. Parlett: "Multiple representations to compute orthogonal eigenvectors of symmetric tridiagonal matrices," Linear Algebra and its Applications, 387(1), pp. 1-28, August 2004.
• Inderjit Dhillon and Beresford Parlett: "Orthogonal Eigenvectors and Relative Gaps," SIAM Journal on Matrix Analysis and Applications, Vol. 25,

1. Also LAPACK Working Note 154.

• Inderjit Dhillon: "A new O(n^2) algorithm for the symmetric tridiagonal eigenvalue/eigenvector problem", Computer Science Division Technical Report No. UCB/CSD-97-971, UC Berkeley, May 1997. Note 1 : DSYEVR calls DSTEMR when the full spectrum is requested on machines which conform to the ieee-754 floating point standard. DSYEVR calls DSTEBZ and DSTEIN on non-ieee machines and when partial spectrum requests are made. Normal execution of DSTEMR may create NaNs and infinities and hence may abort due to a floating point exception in environments which do not handle NaNs and infinities in the ieee standard default manner.

Here is the call graph for this function:

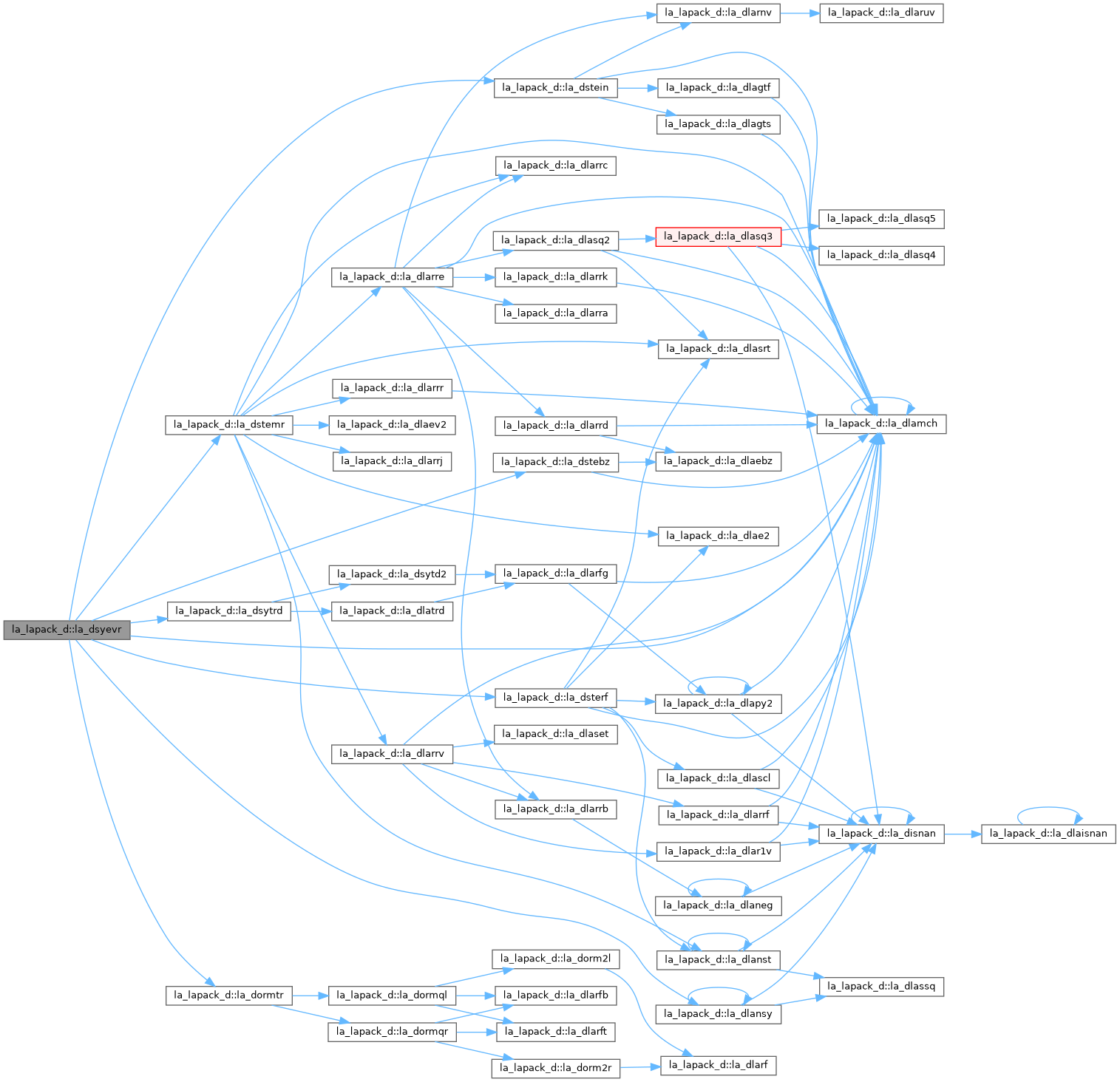
la_dsyevx()

subroutine, public la_lapack_d::la_dsyevx	(	character, intent(in)	jobz,
		character, intent(in)	range,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), intent(in)	vl,
		real(dp), intent(in)	vu,
		integer(ilp), intent(in)	il,
		integer(ilp), intent(in)	iu,
		real(dp), intent(in)	abstol,
		integer(ilp), intent(out)	m,
		real(dp), dimension(*), intent(out)	w,
		real(dp), dimension(ldz,*), intent(out)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), dimension(*), intent(out)	ifail,
		integer(ilp), intent(out)	info
	)

DSYEVX: computes selected eigenvalues and, optionally, eigenvectors of a real symmetric matrix A. Eigenvalues and eigenvectors can be selected by specifying either a range of values or a range of indices for the desired eigenvalues.

Here is the call graph for this function:

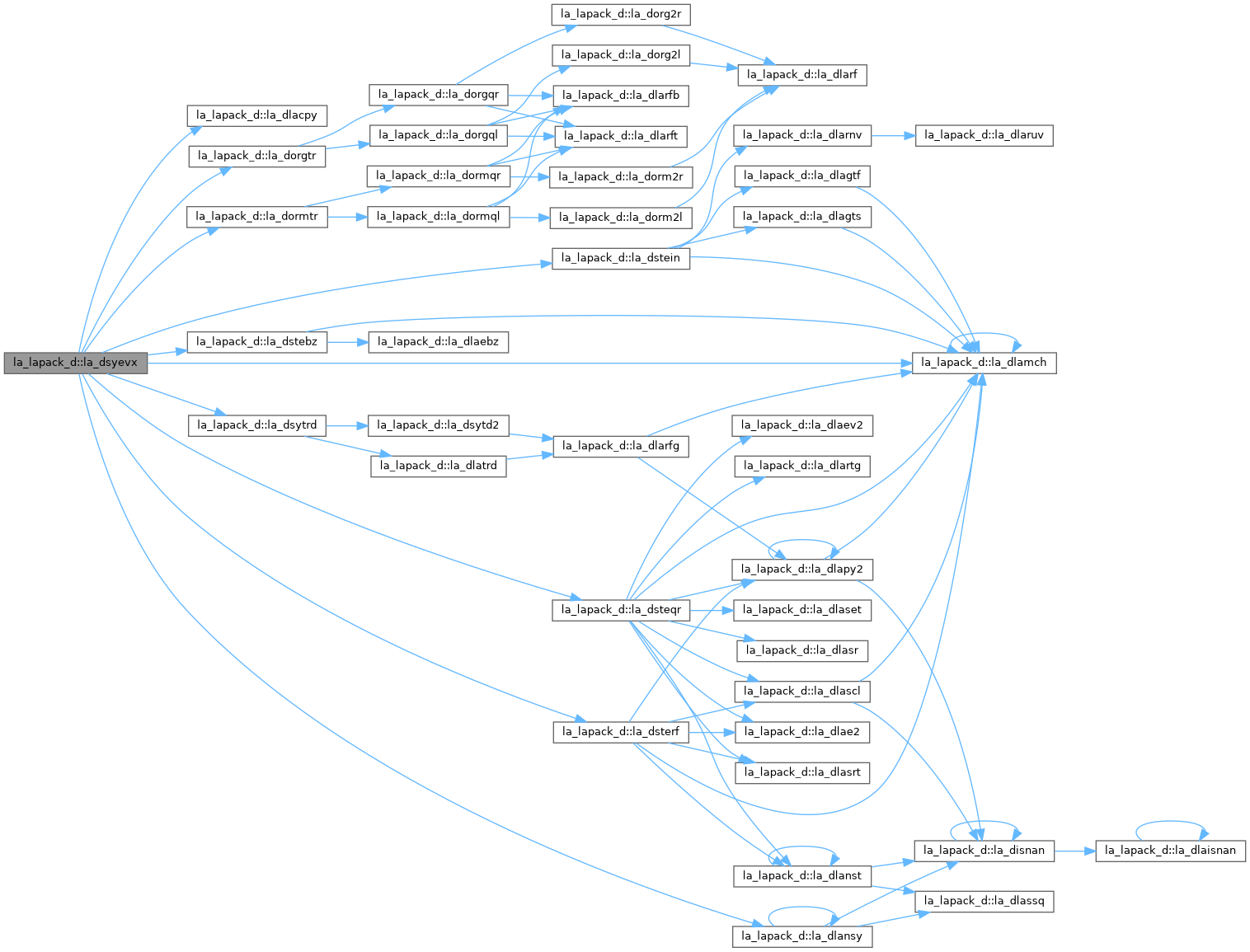
la_dsygs2()

pure subroutine, public la_lapack_d::la_dsygs2	(	integer(ilp), intent(in)	itype,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	info
	)

DSYGS2: reduces a real symmetric-definite generalized eigenproblem to standard form. If ITYPE = 1, the problem is A*x = lambda*B*x, and A is overwritten by inv(U**T)*A*inv(U) or inv(L)*A*inv(L**T) If ITYPE = 2 or 3, the problem is A*B*x = lambda*x or B*A*x = lambda*x, and A is overwritten by U*A*U**T or L**T *A*L. B must have been previously factorized as U**T *U or L*L**T by DPOTRF.

la_dsygst()

pure subroutine, public la_lapack_d::la_dsygst	(	integer(ilp), intent(in)	itype,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	info
	)

DSYGST: reduces a real symmetric-definite generalized eigenproblem to standard form. If ITYPE = 1, the problem is A*x = lambda*B*x, and A is overwritten by inv(U**T)*A*inv(U) or inv(L)*A*inv(L**T) If ITYPE = 2 or 3, the problem is A*B*x = lambda*x or B*A*x = lambda*x, and A is overwritten by U*A*U**T or L**T*A*L. B must have been previously factorized as U**T*U or L*L**T by DPOTRF.

Here is the call graph for this function:

la_dsygv()

subroutine, public la_lapack_d::la_dsygv	(	integer(ilp), intent(in)	itype,
		character, intent(in)	jobz,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(*), intent(out)	w,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DSYGV: computes all the eigenvalues, and optionally, the eigenvectors of a real generalized symmetric-definite eigenproblem, of the form A*x=(lambda)*B*x, A*Bx=(lambda)*x, or B*A*x=(lambda)*x. Here A and B are assumed to be symmetric and B is also positive definite.

Here is the call graph for this function:

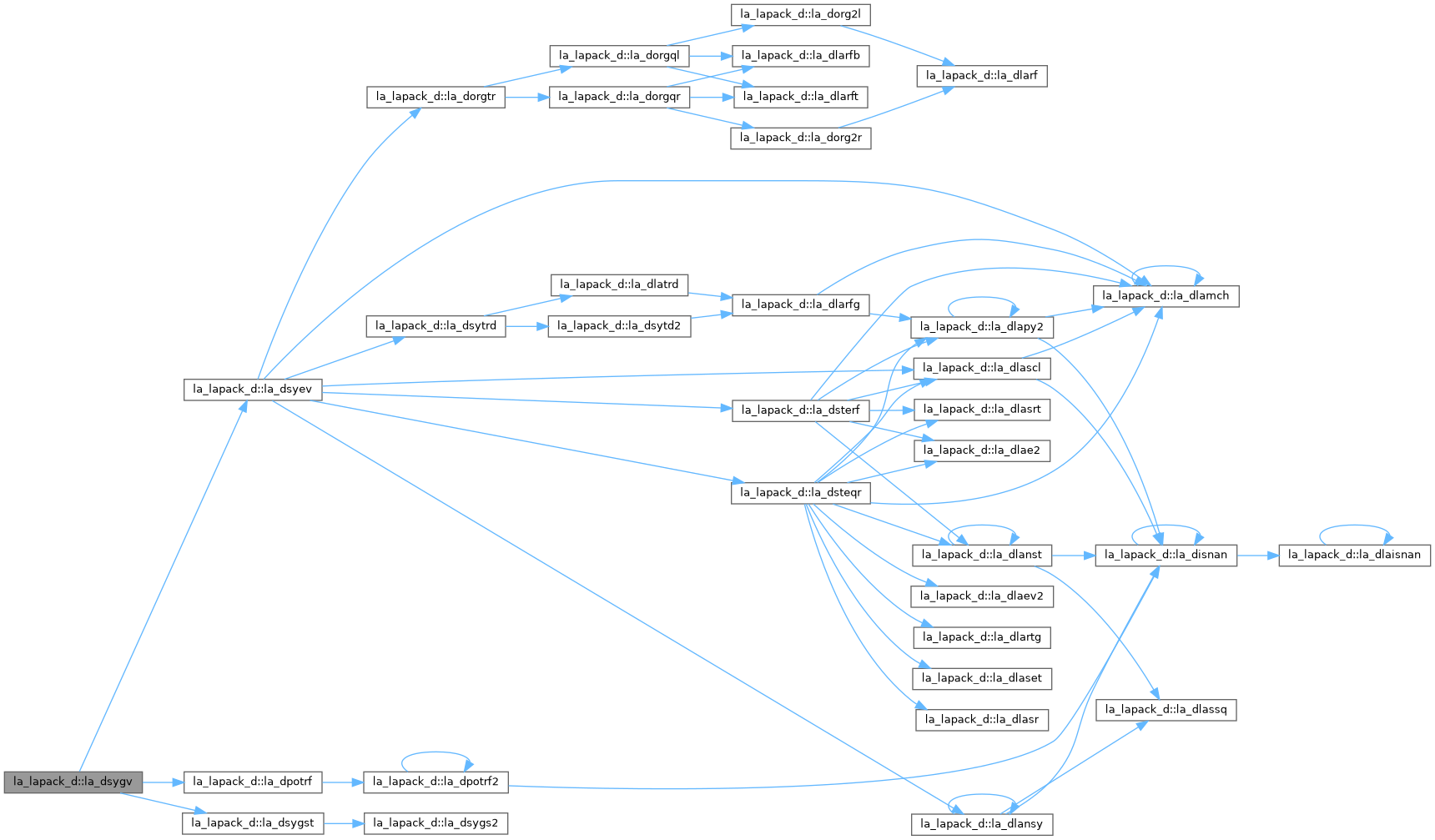
la_dsygvd()

subroutine, public la_lapack_d::la_dsygvd	(	integer(ilp), intent(in)	itype,
		character, intent(in)	jobz,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(*), intent(out)	w,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(in)	liwork,
		integer(ilp), intent(out)	info
	)

DSYGVD: computes all the eigenvalues, and optionally, the eigenvectors of a real generalized symmetric-definite eigenproblem, of the form A*x=(lambda)*B*x, A*Bx=(lambda)*x, or B*A*x=(lambda)*x. Here A and B are assumed to be symmetric and B is also positive definite. If eigenvectors are desired, it uses a divide and conquer algorithm. The divide and conquer algorithm makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none.

Here is the call graph for this function:

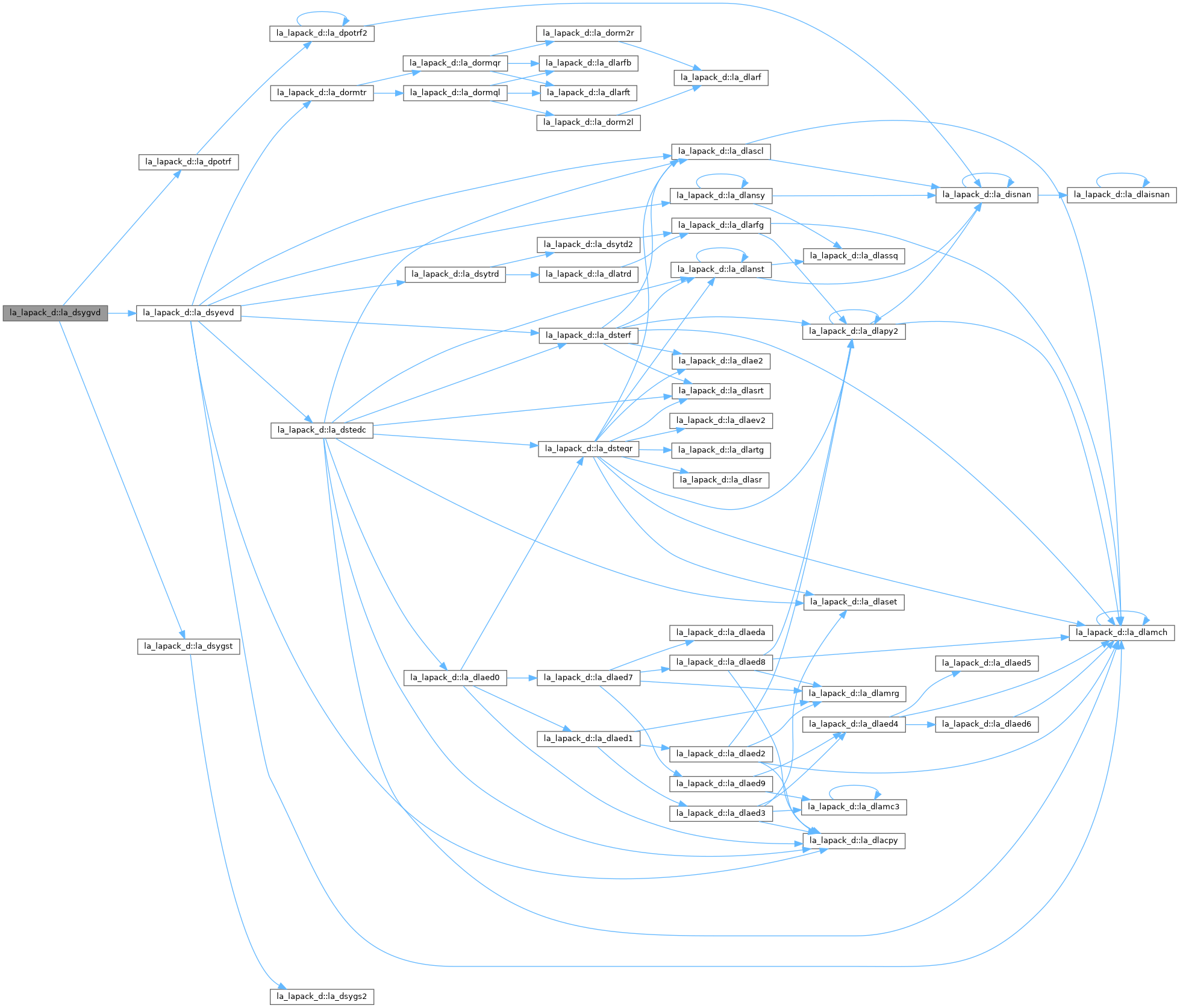
la_dsygvx()

subroutine, public la_lapack_d::la_dsygvx	(	integer(ilp), intent(in)	itype,
		character, intent(in)	jobz,
		character, intent(in)	range,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), intent(in)	vl,
		real(dp), intent(in)	vu,
		integer(ilp), intent(in)	il,
		integer(ilp), intent(in)	iu,
		real(dp), intent(in)	abstol,
		integer(ilp), intent(out)	m,
		real(dp), dimension(*), intent(out)	w,
		real(dp), dimension(ldz,*), intent(out)	z,
		integer(ilp), intent(in)	ldz,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), dimension(*), intent(out)	ifail,
		integer(ilp), intent(out)	info
	)

DSYGVX: computes selected eigenvalues, and optionally, eigenvectors of a real generalized symmetric-definite eigenproblem, of the form A*x=(lambda)*B*x, A*Bx=(lambda)*x, or B*A*x=(lambda)*x. Here A and B are assumed to be symmetric and B is also positive definite. Eigenvalues and eigenvectors can be selected by specifying either a range of values or a range of indices for the desired eigenvalues.

Here is the call graph for this function:

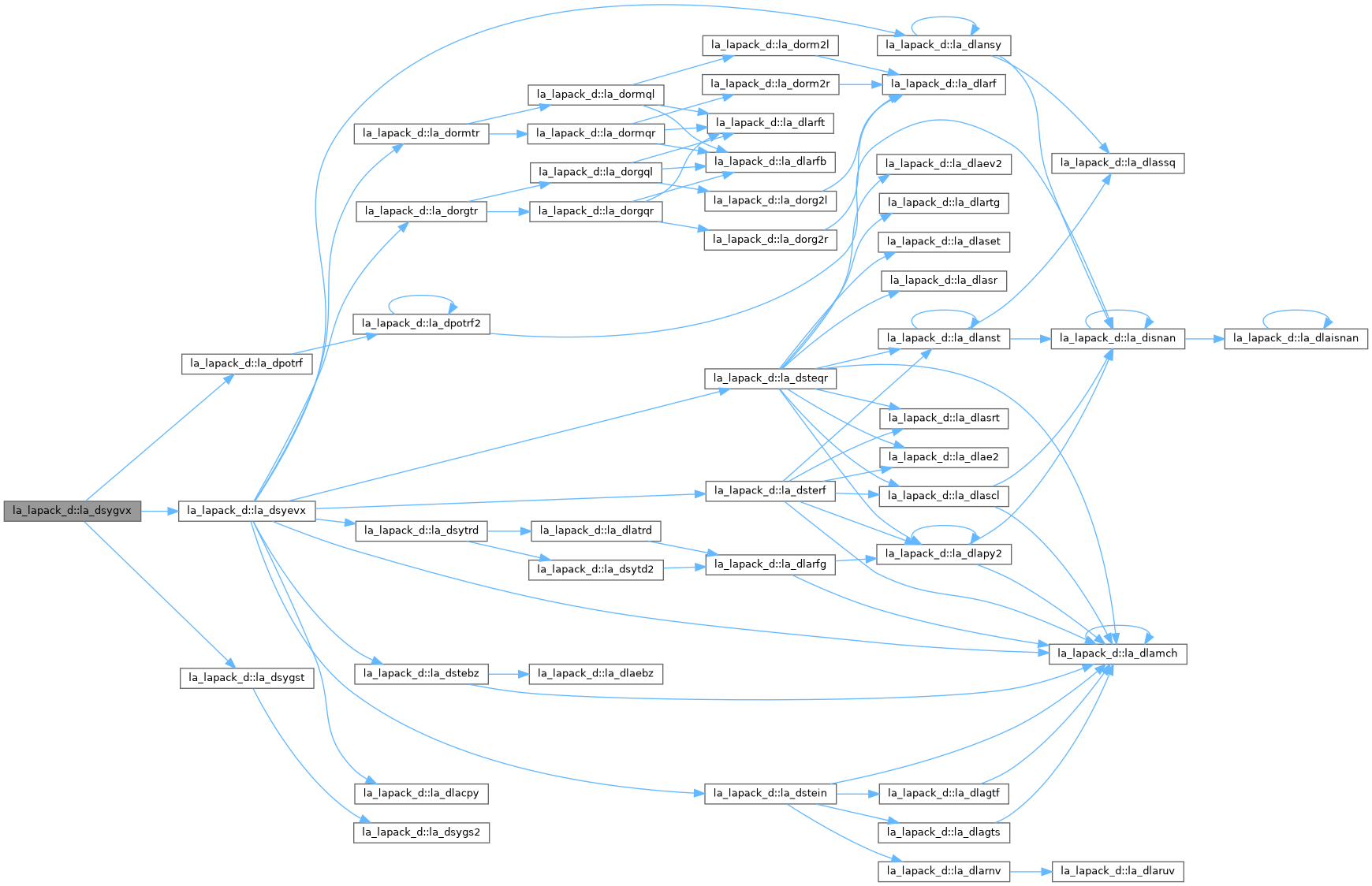
la_dsyrfs()

pure subroutine, public la_lapack_d::la_dsyrfs	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldaf,*), intent(in)	af,
		integer(ilp), intent(in)	ldaf,
		integer(ilp), dimension(*), intent(in)	ipiv,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldx,*), intent(inout)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), dimension(*), intent(out)	ferr,
		real(dp), dimension(*), intent(out)	berr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DSYRFS: improves the computed solution to a system of linear equations when the coefficient matrix is symmetric indefinite, and provides error bounds and backward error estimates for the solution.

Here is the call graph for this function:

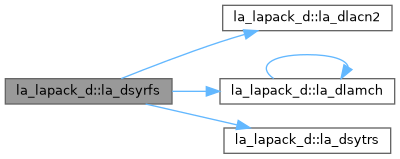
la_dsysv()

pure subroutine, public la_lapack_d::la_dsysv	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(out)	ipiv,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DSYSV: computes the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric matrix and X and B are N-by-NRHS matrices. The diagonal pivoting method is used to factor A as A = U * D * U**T, if UPLO = 'U', or A = L * D * L**T, if UPLO = 'L', where U (or L) is a product of permutation and unit upper (lower) triangular matrices, and D is symmetric and block diagonal with 1-by-1 and 2-by-2 diagonal blocks. The factored form of A is then used to solve the system of equations A * X = B.

Here is the call graph for this function:

la_dsysv_aa()

pure subroutine, public la_lapack_d::la_dsysv_aa	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(out)	ipiv,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DSYSV computes the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric matrix and X and B are N-by-NRHS matrices. Aasen's algorithm is used to factor A as A = U**T * T * U, if UPLO = 'U', or A = L * T * L**T, if UPLO = 'L', where U (or L) is a product of permutation and unit upper (lower) triangular matrices, and T is symmetric tridiagonal. The factored form of A is then used to solve the system of equations A * X = B.

Here is the call graph for this function:

la_dsysv_rk()

pure subroutine, public la_lapack_d::la_dsysv_rk	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	e,
		integer(ilp), dimension(*), intent(out)	ipiv,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DSYSV_RK: computes the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric matrix and X and B are N-by-NRHS matrices. The bounded Bunch-Kaufman (rook) diagonal pivoting method is used to factor A as A = P*U*D*(U**T)*(P**T), if UPLO = 'U', or A = P*L*D*(L**T)*(P**T), if UPLO = 'L', where U (or L) is unit upper (or lower) triangular matrix, U**T (or L**T) is the transpose of U (or L), P is a permutation matrix, P**T is the transpose of P, and D is symmetric and block diagonal with 1-by-1 and 2-by-2 diagonal blocks. DSYTRF_RK is called to compute the factorization of a real symmetric matrix. The factored form of A is then used to solve the system of equations A * X = B by calling BLAS3 routine DSYTRS_3.

Here is the call graph for this function:

la_dsysv_rook()

pure subroutine, public la_lapack_d::la_dsysv_rook	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(out)	ipiv,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DSYSV_ROOK: computes the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric matrix and X and B are N-by-NRHS matrices. The diagonal pivoting method is used to factor A as A = U * D * U**T, if UPLO = 'U', or A = L * D * L**T, if UPLO = 'L', where U (or L) is a product of permutation and unit upper (lower) triangular matrices, and D is symmetric and block diagonal with 1-by-1 and 2-by-2 diagonal blocks. DSYTRF_ROOK is called to compute the factorization of a real symmetric matrix A using the bounded Bunch-Kaufman ("rook") diagonal pivoting method. The factored form of A is then used to solve the system of equations A * X = B by calling DSYTRS_ROOK.

Here is the call graph for this function:

la_dsysvx()

subroutine, public la_lapack_d::la_dsysvx	(	character, intent(in)	fact,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldaf,*), intent(inout)	af,
		integer(ilp), intent(in)	ldaf,
		integer(ilp), dimension(*), intent(inout)	ipiv,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldx,*), intent(out)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), intent(out)	rcond,
		real(dp), dimension(*), intent(out)	ferr,
		real(dp), dimension(*), intent(out)	berr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DSYSVX: uses the diagonal pivoting factorization to compute the solution to a real system of linear equations A * X = B, where A is an N-by-N symmetric matrix and X and B are N-by-NRHS matrices. Error bounds on the solution and a condition estimate are also provided.

Here is the call graph for this function:

la_dsyswapr()

pure subroutine, public la_lapack_d::la_dsyswapr	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,n), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), intent(in)	i1,
		integer(ilp), intent(in)	i2
	)

DSYSWAPR: applies an elementary permutation on the rows and the columns of a symmetric matrix.

la_dsytd2()

pure subroutine, public la_lapack_d::la_dsytd2	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	d,
		real(dp), dimension(*), intent(out)	e,
		real(dp), dimension(*), intent(out)	tau,
		integer(ilp), intent(out)	info
	)

DSYTD2: reduces a real symmetric matrix A to symmetric tridiagonal form T by an orthogonal similarity transformation: Q**T * A * Q = T.

Here is the call graph for this function:

la_dsytf2()

pure subroutine, public la_lapack_d::la_dsytf2	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(out)	ipiv,
		integer(ilp), intent(out)	info
	)

DSYTF2: computes the factorization of a real symmetric matrix A using the Bunch-Kaufman diagonal pivoting method: A = U*D*U**T or A = L*D*L**T where U (or L) is a product of permutation and unit upper (lower) triangular matrices, U**T is the transpose of U, and D is symmetric and block diagonal with 1-by-1 and 2-by-2 diagonal blocks. This is the unblocked version of the algorithm, calling Level 2 BLAS.

Here is the call graph for this function:

la_dsytf2_rk()

pure subroutine, public la_lapack_d::la_dsytf2_rk	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	e,
		integer(ilp), dimension(*), intent(out)	ipiv,
		integer(ilp), intent(out)	info
	)

DSYTF2_RK: computes the factorization of a real symmetric matrix A using the bounded Bunch-Kaufman (rook) diagonal pivoting method: A = P*U*D*(U**T)*(P**T) or A = P*L*D*(L**T)*(P**T), where U (or L) is unit upper (or lower) triangular matrix, U**T (or L**T) is the transpose of U (or L), P is a permutation matrix, P**T is the transpose of P, and D is symmetric and block diagonal with 1-by-1 and 2-by-2 diagonal blocks. This is the unblocked version of the algorithm, calling Level 2 BLAS. For more information see Further Details section.

Here is the call graph for this function:

la_dsytf2_rook()

pure subroutine, public la_lapack_d::la_dsytf2_rook	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(out)	ipiv,
		integer(ilp), intent(out)	info
	)

DSYTF2_ROOK: computes the factorization of a real symmetric matrix A using the bounded Bunch-Kaufman ("rook") diagonal pivoting method: A = U*D*U**T or A = L*D*L**T where U (or L) is a product of permutation and unit upper (lower) triangular matrices, U**T is the transpose of U, and D is symmetric and block diagonal with 1-by-1 and 2-by-2 diagonal blocks. This is the unblocked version of the algorithm, calling Level 2 BLAS.

Here is the call graph for this function:

la_dsytrd()

pure subroutine, public la_lapack_d::la_dsytrd	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	d,
		real(dp), dimension(*), intent(out)	e,
		real(dp), dimension(*), intent(out)	tau,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DSYTRD: reduces a real symmetric matrix A to real symmetric tridiagonal form T by an orthogonal similarity transformation: Q**T * A * Q = T.

Here is the call graph for this function:

la_dsytrd_sb2st()

pure subroutine, public la_lapack_d::la_dsytrd_sb2st	(	character, intent(in)	stage1,
		character, intent(in)	vect,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kd,
		real(dp), dimension(ldab,*), intent(inout)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(*), intent(out)	d,
		real(dp), dimension(*), intent(out)	e,
		real(dp), dimension(*), intent(out)	hous,
		integer(ilp), intent(in)	lhous,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DSYTRD_SB2ST: reduces a real symmetric band matrix A to real symmetric tridiagonal form T by a orthogonal similarity transformation: Q**T * A * Q = T.

Here is the call graph for this function:

la_dsytrd_sy2sb()

pure subroutine, public la_lapack_d::la_dsytrd_sy2sb	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kd,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldab,*), intent(out)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(*), intent(out)	tau,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DSYTRD_SY2SB: reduces a real symmetric matrix A to real symmetric band-diagonal form AB by a orthogonal similarity transformation: Q**T * A * Q = AB.

Here is the call graph for this function:

la_dsytrf()

pure subroutine, public la_lapack_d::la_dsytrf	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(out)	ipiv,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DSYTRF: computes the factorization of a real symmetric matrix A using the Bunch-Kaufman diagonal pivoting method. The form of the factorization is A = U**T*D*U or A = L*D*L**T where U (or L) is a product of permutation and unit upper (lower) triangular matrices, and D is symmetric and block diagonal with 1-by-1 and 2-by-2 diagonal blocks. This is the blocked version of the algorithm, calling Level 3 BLAS.

Here is the call graph for this function:

la_dsytrf_aa()

pure subroutine, public la_lapack_d::la_dsytrf_aa	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(out)	ipiv,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DSYTRF_AA: computes the factorization of a real symmetric matrix A using the Aasen's algorithm. The form of the factorization is A = U**T*T*U or A = L*T*L**T where U (or L) is a product of permutation and unit upper (lower) triangular matrices, and T is a symmetric tridiagonal matrix. This is the blocked version of the algorithm, calling Level 3 BLAS.

Here is the call graph for this function:

la_dsytrf_rk()

pure subroutine, public la_lapack_d::la_dsytrf_rk	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	e,
		integer(ilp), dimension(*), intent(out)	ipiv,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DSYTRF_RK: computes the factorization of a real symmetric matrix A using the bounded Bunch-Kaufman (rook) diagonal pivoting method: A = P*U*D*(U**T)*(P**T) or A = P*L*D*(L**T)*(P**T), where U (or L) is unit upper (or lower) triangular matrix, U**T (or L**T) is the transpose of U (or L), P is a permutation matrix, P**T is the transpose of P, and D is symmetric and block diagonal with 1-by-1 and 2-by-2 diagonal blocks. This is the blocked version of the algorithm, calling Level 3 BLAS. For more information see Further Details section.

Here is the call graph for this function:

la_dsytrf_rook()

pure subroutine, public la_lapack_d::la_dsytrf_rook	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(out)	ipiv,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DSYTRF_ROOK: computes the factorization of a real symmetric matrix A using the bounded Bunch-Kaufman ("rook") diagonal pivoting method. The form of the factorization is A = U*D*U**T or A = L*D*L**T where U (or L) is a product of permutation and unit upper (lower) triangular matrices, and D is symmetric and block diagonal with 1-by-1 and 2-by-2 diagonal blocks. This is the blocked version of the algorithm, calling Level 3 BLAS.

Here is the call graph for this function:

la_dsytri()

pure subroutine, public la_lapack_d::la_dsytri	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(in)	ipiv,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DSYTRI: computes the inverse of a real symmetric indefinite matrix A using the factorization A = U*D*U**T or A = L*D*L**T computed by DSYTRF.

la_dsytri_rook()

pure subroutine, public la_lapack_d::la_dsytri_rook	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(in)	ipiv,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DSYTRI_ROOK: computes the inverse of a real symmetric matrix A using the factorization A = U*D*U**T or A = L*D*L**T computed by DSYTRF_ROOK.

la_dsytrs()

pure subroutine, public la_lapack_d::la_dsytrs	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(in)	ipiv,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	info
	)

DSYTRS: solves a system of linear equations A*X = B with a real symmetric matrix A using the factorization A = U*D*U**T or A = L*D*L**T computed by DSYTRF.

la_dsytrs2()

pure subroutine, public la_lapack_d::la_dsytrs2	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(in)	ipiv,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DSYTRS2: solves a system of linear equations A*X = B with a real symmetric matrix A using the factorization A = U*D*U**T or A = L*D*L**T computed by DSYTRF and converted by DSYCONV.

Here is the call graph for this function:

la_dsytrs_3()

pure subroutine, public la_lapack_d::la_dsytrs_3	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(in)	e,
		integer(ilp), dimension(*), intent(in)	ipiv,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	info
	)

DSYTRS_3: solves a system of linear equations A * X = B with a real symmetric matrix A using the factorization computed by DSYTRF_RK or DSYTRF_BK: A = P*U*D*(U**T)*(P**T) or A = P*L*D*(L**T)*(P**T), where U (or L) is unit upper (or lower) triangular matrix, U**T (or L**T) is the transpose of U (or L), P is a permutation matrix, P**T is the transpose of P, and D is symmetric and block diagonal with 1-by-1 and 2-by-2 diagonal blocks. This algorithm is using Level 3 BLAS.

la_dsytrs_aa()

pure subroutine, public la_lapack_d::la_dsytrs_aa	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(in)	ipiv,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DSYTRS_AA: solves a system of linear equations A*X = B with a real symmetric matrix A using the factorization A = U**T*T*U or A = L*T*L**T computed by DSYTRF_AA.

Here is the call graph for this function:

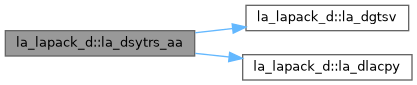
la_dsytrs_rook()

pure subroutine, public la_lapack_d::la_dsytrs_rook	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(in)	ipiv,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	info
	)

DSYTRS_ROOK: solves a system of linear equations A*X = B with a real symmetric matrix A using the factorization A = U*D*U**T or A = L*D*L**T computed by DSYTRF_ROOK.

la_dtbcon()

subroutine, public la_lapack_d::la_dtbcon	(	character, intent(in)	norm,
		character, intent(in)	uplo,
		character, intent(in)	diag,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kd,
		real(dp), dimension(ldab,*), intent(in)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), intent(out)	rcond,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DTBCON: estimates the reciprocal of the condition number of a triangular band matrix A, in either the 1-norm or the infinity-norm. The norm of A is computed and an estimate is obtained for norm(inv(A)), then the reciprocal of the condition number is computed as RCOND = 1 / ( norm(A) * norm(inv(A)) ).

Here is the call graph for this function:

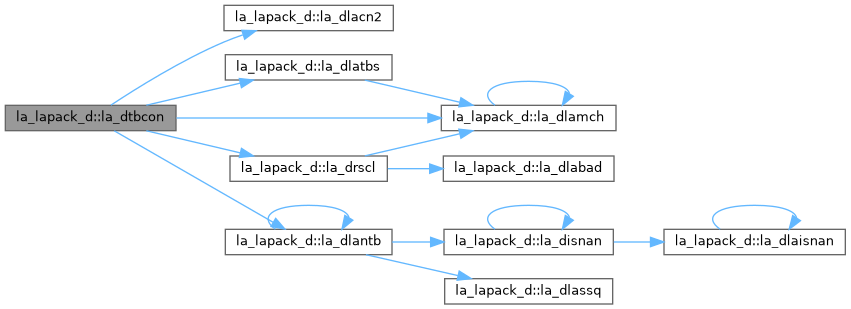
la_dtbrfs()

pure subroutine, public la_lapack_d::la_dtbrfs	(	character, intent(in)	uplo,
		character, intent(in)	trans,
		character, intent(in)	diag,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kd,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(ldab,*), intent(in)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldx,*), intent(in)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), dimension(*), intent(out)	ferr,
		real(dp), dimension(*), intent(out)	berr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DTBRFS: provides error bounds and backward error estimates for the solution to a system of linear equations with a triangular band coefficient matrix. The solution matrix X must be computed by DTBTRS or some other means before entering this routine. DTBRFS does not do iterative refinement because doing so cannot improve the backward error.

Here is the call graph for this function:

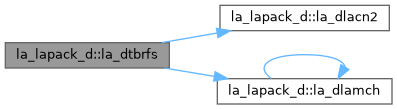
la_dtbtrs()

pure subroutine, public la_lapack_d::la_dtbtrs	(	character, intent(in)	uplo,
		character, intent(in)	trans,
		character, intent(in)	diag,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	kd,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(ldab,*), intent(in)	ab,
		integer(ilp), intent(in)	ldab,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	info
	)

DTBTRS: solves a triangular system of the form A * X = B or A**T * X = B, where A is a triangular band matrix of order N, and B is an N-by NRHS matrix. A check is made to verify that A is nonsingular.

la_dtfsm()

pure subroutine, public la_lapack_d::la_dtfsm	(	character, intent(in)	transr,
		character, intent(in)	side,
		character, intent(in)	uplo,
		character, intent(in)	trans,
		character, intent(in)	diag,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), intent(in)	alpha,
		real(dp), dimension(0:*), intent(in)	a,
		real(dp), dimension(0:ldb - 1,0:*), intent(inout)	b,
		integer(ilp), intent(in)	ldb
	)

Level 3 BLAS like routine for A in RFP Format. DTFSM: solves the matrix equation op( A )*X = alpha*B or X*op( A ) = alpha*B where alpha is a scalar, X and B are m by n matrices, A is a unit, or non-unit, upper or lower triangular matrix and op( A ) is one of op( A ) = A or op( A ) = A**T. A is in Rectangular Full Packed (RFP) Format. The matrix X is overwritten on B.

la_dtftri()

pure subroutine, public la_lapack_d::la_dtftri	(	character, intent(in)	transr,
		character, intent(in)	uplo,
		character, intent(in)	diag,
		integer(ilp), intent(in)	n,
		real(dp), dimension(0:*), intent(inout)	a,
		integer(ilp), intent(out)	info
	)

DTFTRI: computes the inverse of a triangular matrix A stored in RFP format. This is a Level 3 BLAS version of the algorithm.

Here is the call graph for this function:

la_dtfttp()

pure subroutine, public la_lapack_d::la_dtfttp	(	character, intent(in)	transr,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(0:*), intent(in)	arf,
		real(dp), dimension(0:*), intent(out)	ap,
		integer(ilp), intent(out)	info
	)

DTFTTP: copies a triangular matrix A from rectangular full packed format (TF) to standard packed format (TP).

la_dtfttr()

pure subroutine, public la_lapack_d::la_dtfttr	(	character, intent(in)	transr,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(0:*), intent(in)	arf,
		real(dp), dimension(0:lda - 1,0:*), intent(out)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), intent(out)	info
	)

DTFTTR: copies a triangular matrix A from rectangular full packed format (TF) to standard full format (TR).

la_dtgevc()

pure subroutine, public la_lapack_d::la_dtgevc	(	character, intent(in)	side,
		character, intent(in)	howmny,
		logical(lk), dimension(*), intent(in)	select,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lds,*), intent(in)	s,
		integer(ilp), intent(in)	lds,
		real(dp), dimension(ldp,*), intent(in)	p,
		integer(ilp), intent(in)	ldp,
		real(dp), dimension(ldvl,*), intent(inout)	vl,
		integer(ilp), intent(in)	ldvl,
		real(dp), dimension(ldvr,*), intent(inout)	vr,
		integer(ilp), intent(in)	ldvr,
		integer(ilp), intent(in)	mm,
		integer(ilp), intent(out)	m,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DTGEVC: computes some or all of the right and/or left eigenvectors of a pair of real matrices (S,P), where S is a quasi-triangular matrix and P is upper triangular. Matrix pairs of this type are produced by the generalized Schur factorization of a matrix pair (A,B): A = Q*S*Z**T, B = Q*P*Z**T as computed by DGGHRD + DHGEQZ. The right eigenvector x and the left eigenvector y of (S,P) corresponding to an eigenvalue w are defined by: S*x = w*P*x, (y**H)*S = w*(y**H)*P, where y**H denotes the conjugate tranpose of y. The eigenvalues are not input to this routine, but are computed directly from the diagonal blocks of S and P. This routine returns the matrices X and/or Y of right and left eigenvectors of (S,P), or the products Z*X and/or Q*Y, where Z and Q are input matrices. If Q and Z are the orthogonal factors from the generalized Schur factorization of a matrix pair (A,B), then Z*X and Q*Y are the matrices of right and left eigenvectors of (A,B).

Here is the call graph for this function:

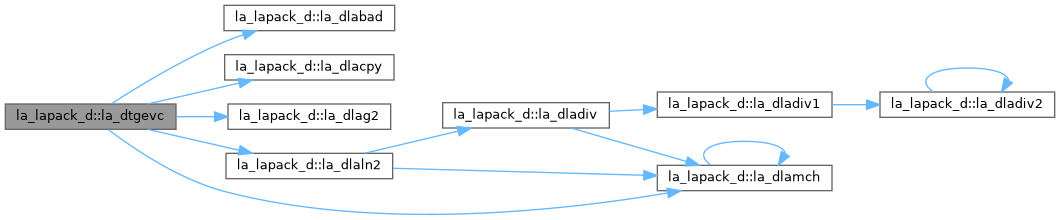
la_dtgex2()

pure subroutine, public la_lapack_d::la_dtgex2	(	logical(lk), intent(in)	wantq,
		logical(lk), intent(in)	wantz,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldq,*), intent(inout)	q,
		integer(ilp), intent(in)	ldq,
		real(dp), dimension(ldz,*), intent(inout)	z,
		integer(ilp), intent(in)	ldz,
		integer(ilp), intent(in)	j1,
		integer(ilp), intent(in)	n1,
		integer(ilp), intent(in)	n2,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DTGEX2: swaps adjacent diagonal blocks (A11, B11) and (A22, B22) of size 1-by-1 or 2-by-2 in an upper (quasi) triangular matrix pair (A, B) by an orthogonal equivalence transformation. (A, B) must be in generalized real Schur canonical form (as returned by DGGES), i.e. A is block upper triangular with 1-by-1 and 2-by-2 diagonal blocks. B is upper triangular. Optionally, the matrices Q and Z of generalized Schur vectors are updated. Q(in) * A(in) * Z(in)**T = Q(out) * A(out) * Z(out)**T Q(in) * B(in) * Z(in)**T = Q(out) * B(out) * Z(out)**T.

Here is the call graph for this function:

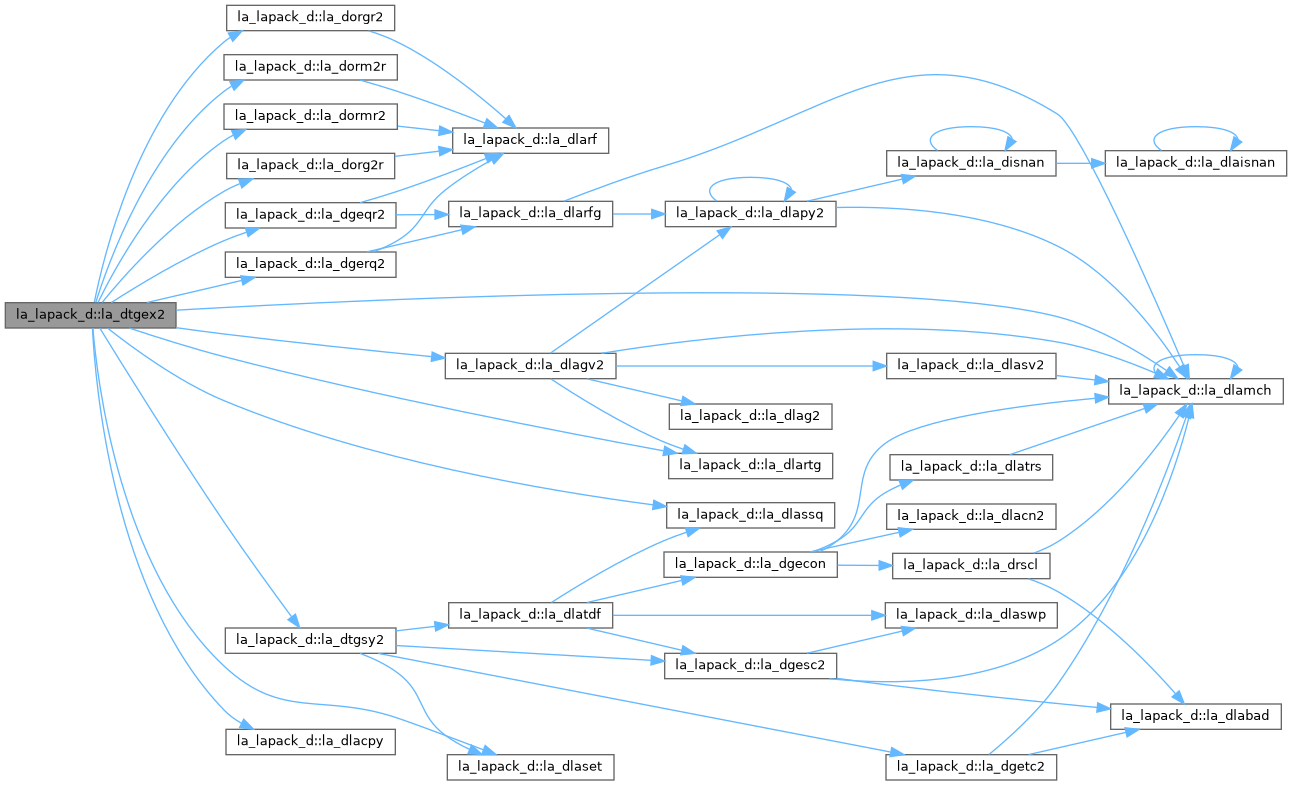
la_dtgexc()

pure subroutine, public la_lapack_d::la_dtgexc	(	logical(lk), intent(in)	wantq,
		logical(lk), intent(in)	wantz,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldq,*), intent(inout)	q,
		integer(ilp), intent(in)	ldq,
		real(dp), dimension(ldz,*), intent(inout)	z,
		integer(ilp), intent(in)	ldz,
		integer(ilp), intent(inout)	ifst,
		integer(ilp), intent(inout)	ilst,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DTGEXC: reorders the generalized real Schur decomposition of a real matrix pair (A,B) using an orthogonal equivalence transformation (A, B) = Q * (A, B) * Z**T, so that the diagonal block of (A, B) with row index IFST is moved to row ILST. (A, B) must be in generalized real Schur canonical form (as returned by DGGES), i.e. A is block upper triangular with 1-by-1 and 2-by-2 diagonal blocks. B is upper triangular. Optionally, the matrices Q and Z of generalized Schur vectors are updated. Q(in) * A(in) * Z(in)**T = Q(out) * A(out) * Z(out)**T Q(in) * B(in) * Z(in)**T = Q(out) * B(out) * Z(out)**T.

Here is the call graph for this function:

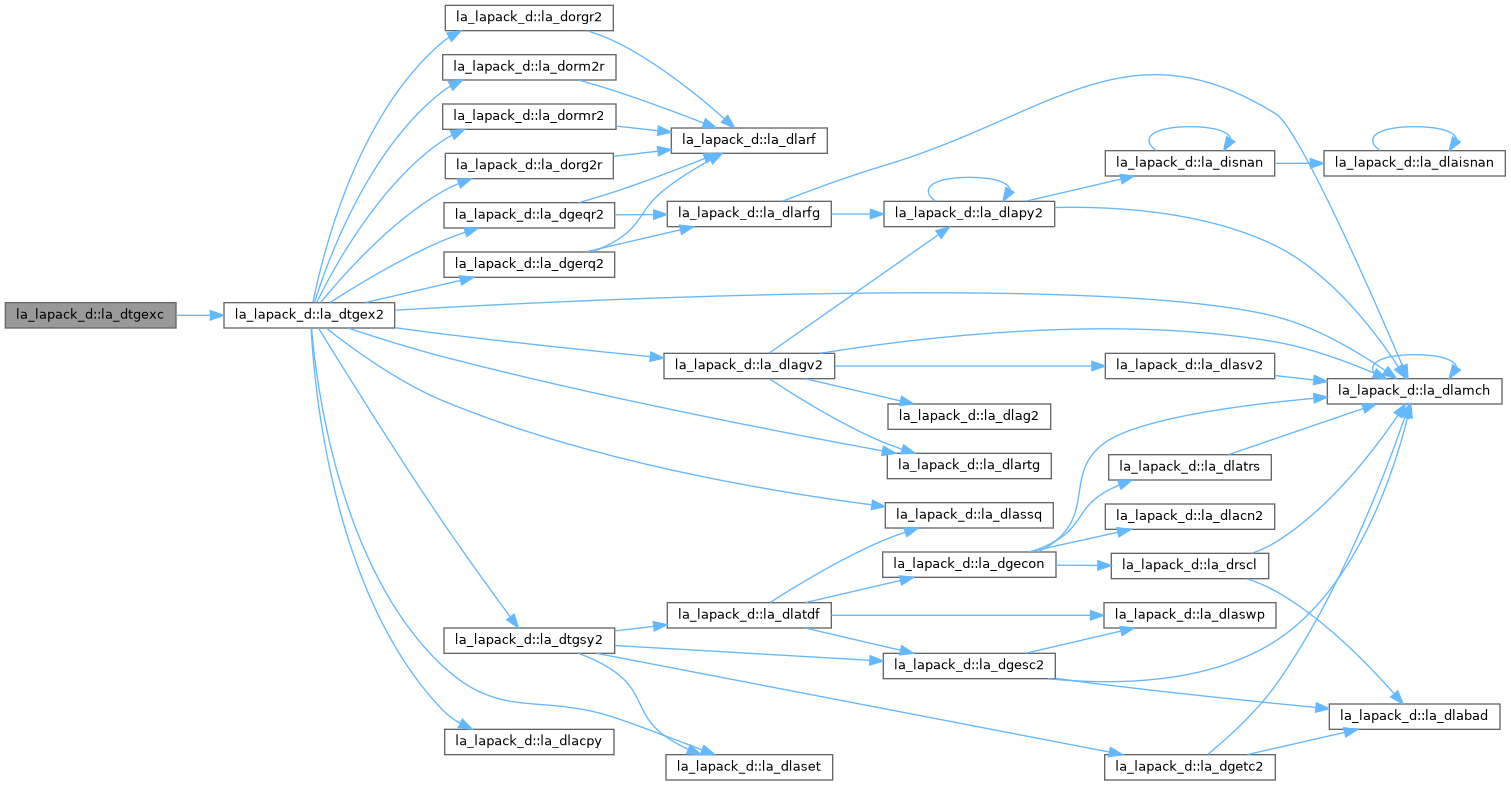
la_dtgsen()

pure subroutine, public la_lapack_d::la_dtgsen	(	integer(ilp), intent(in)	ijob,
		logical(lk), intent(in)	wantq,
		logical(lk), intent(in)	wantz,
		logical(lk), dimension(*), intent(in)	select,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(*), intent(out)	alphar,
		real(dp), dimension(*), intent(out)	alphai,
		real(dp), dimension(*), intent(out)	beta,
		real(dp), dimension(ldq,*), intent(inout)	q,
		integer(ilp), intent(in)	ldq,
		real(dp), dimension(ldz,*), intent(inout)	z,
		integer(ilp), intent(in)	ldz,
		integer(ilp), intent(out)	m,
		real(dp), intent(out)	pl,
		real(dp), intent(out)	pr,
		real(dp), dimension(*), intent(out)	dif,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(in)	liwork,
		integer(ilp), intent(out)	info
	)

DTGSEN: reorders the generalized real Schur decomposition of a real matrix pair (A, B) (in terms of an orthonormal equivalence trans- formation Q**T * (A, B) * Z), so that a selected cluster of eigenvalues appears in the leading diagonal blocks of the upper quasi-triangular matrix A and the upper triangular B. The leading columns of Q and Z form orthonormal bases of the corresponding left and right eigen- spaces (deflating subspaces). (A, B) must be in generalized real Schur canonical form (as returned by DGGES), i.e. A is block upper triangular with 1-by-1 and 2-by-2 diagonal blocks. B is upper triangular. DTGSEN also computes the generalized eigenvalues w(j) = (ALPHAR(j) + i*ALPHAI(j))/BETA(j) of the reordered matrix pair (A, B). Optionally, DTGSEN computes the estimates of reciprocal condition numbers for eigenvalues and eigenspaces. These are Difu[(A11,B11), (A22,B22)] and Difl[(A11,B11), (A22,B22)], i.e. the separation(s) between the matrix pairs (A11, B11) and (A22,B22) that correspond to the selected cluster and the eigenvalues outside the cluster, resp., and norms of "projections" onto left and right eigenspaces w.r.t. the selected cluster in the (1,1)-block.

Here is the call graph for this function:

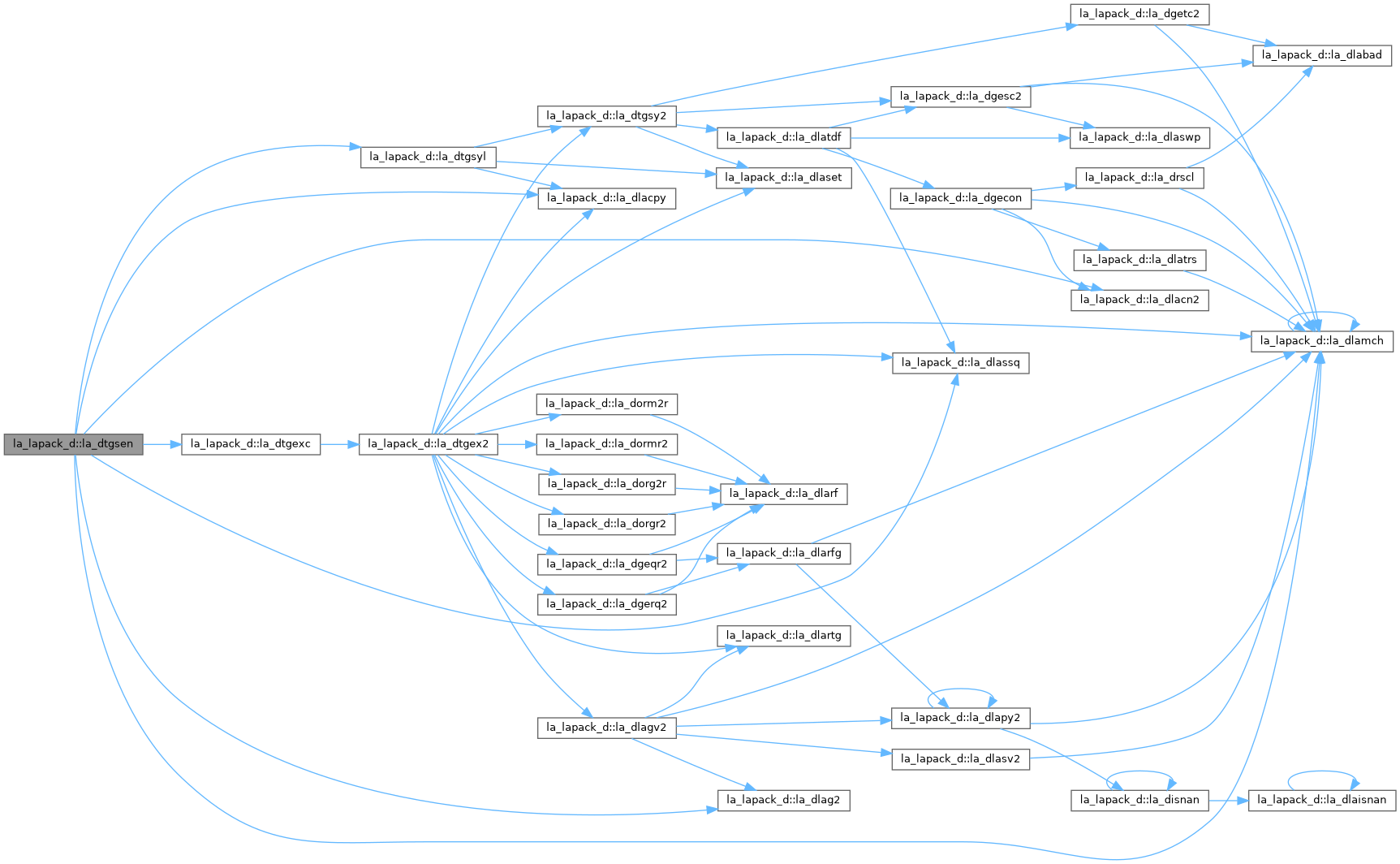
la_dtgsja()

pure subroutine, public la_lapack_d::la_dtgsja	(	character, intent(in)	jobu,
		character, intent(in)	jobv,
		character, intent(in)	jobq,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	p,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		integer(ilp), intent(in)	l,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), intent(in)	tola,
		real(dp), intent(in)	tolb,
		real(dp), dimension(*), intent(out)	alpha,
		real(dp), dimension(*), intent(out)	beta,
		real(dp), dimension(ldu,*), intent(inout)	u,
		integer(ilp), intent(in)	ldu,
		real(dp), dimension(ldv,*), intent(inout)	v,
		integer(ilp), intent(in)	ldv,
		real(dp), dimension(ldq,*), intent(inout)	q,
		integer(ilp), intent(in)	ldq,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	ncycle,
		integer(ilp), intent(out)	info
	)

DTGSJA: computes the generalized singular value decomposition (GSVD) of two real upper triangular (or trapezoidal) matrices A and B. On entry, it is assumed that matrices A and B have the following forms, which may be obtained by the preprocessing subroutine DGGSVP from a general M-by-N matrix A and P-by-N matrix B: N-K-L K L A = K ( 0 A12 A13 ) if M-K-L >= 0; L ( 0 0 A23 ) M-K-L ( 0 0 0 ) N-K-L K L A = K ( 0 A12 A13 ) if M-K-L < 0; M-K ( 0 0 A23 ) N-K-L K L B = L ( 0 0 B13 ) P-L ( 0 0 0 ) where the K-by-K matrix A12 and L-by-L matrix B13 are nonsingular upper triangular; A23 is L-by-L upper triangular if M-K-L >= 0, otherwise A23 is (M-K)-by-L upper trapezoidal. On exit, U**T A*Q = D1( 0 R ), V**T B*Q = D2( 0 R ), where U, V and Q are orthogonal matrices. R is a nonsingular upper triangular matrix, and D1 and D2 are `‘diagonal’' matrices, which are of the following structures: If M-K-L >= 0, K L D1 = K ( I 0 ) L ( 0 C ) M-K-L ( 0 0 ) K L D2 = L ( 0 S ) P-L ( 0 0 ) N-K-L K L ( 0 R ) = K ( 0 R11 R12 ) K L ( 0 0 R22 ) L where C = diag( ALPHA(K+1), ... , ALPHA(K+L) ), S = diag( BETA(K+1), ... , BETA(K+L) ), C**2 + S**2 = I. R is stored in A(1:K+L,N-K-L+1:N) on exit. If M-K-L < 0, K M-K K+L-M D1 = K ( I 0 0 ) M-K ( 0 C 0 ) K M-K K+L-M D2 = M-K ( 0 S 0 ) K+L-M ( 0 0 I ) P-L ( 0 0 0 ) N-K-L K M-K K+L-M ( 0 R ) = K ( 0 R11 R12 R13 ) M-K ( 0 0 R22 R23 ) K+L-M ( 0 0 0 R33 ) where C = diag( ALPHA(K+1), ... , ALPHA(M) ), S = diag( BETA(K+1), ... , BETA(M) ), C**2 + S**2 = I. R = ( R11 R12 R13 ) is stored in A(1:M, N-K-L+1:N) and R33 is stored ( 0 R22 R23 ) in B(M-K+1:L,N+M-K-L+1:N) on exit. The computation of the orthogonal transformation matrices U, V or Q is optional. These matrices may either be formed explicitly, or they may be postmultiplied into input matrices U1, V1, or Q1.

Here is the call graph for this function:

la_dtgsna()

pure subroutine, public la_lapack_d::la_dtgsna	(	character, intent(in)	job,
		character, intent(in)	howmny,
		logical(lk), dimension(*), intent(in)	select,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldvl,*), intent(in)	vl,
		integer(ilp), intent(in)	ldvl,
		real(dp), dimension(ldvr,*), intent(in)	vr,
		integer(ilp), intent(in)	ldvr,
		real(dp), dimension(*), intent(out)	s,
		real(dp), dimension(*), intent(out)	dif,
		integer(ilp), intent(in)	mm,
		integer(ilp), intent(out)	m,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DTGSNA: estimates reciprocal condition numbers for specified eigenvalues and/or eigenvectors of a matrix pair (A, B) in generalized real Schur canonical form (or of any matrix pair (Q*A*Z**T, Q*B*Z**T) with orthogonal matrices Q and Z, where Z**T denotes the transpose of Z. (A, B) must be in generalized real Schur form (as returned by DGGES), i.e. A is block upper triangular with 1-by-1 and 2-by-2 diagonal blocks. B is upper triangular.

Here is the call graph for this function:

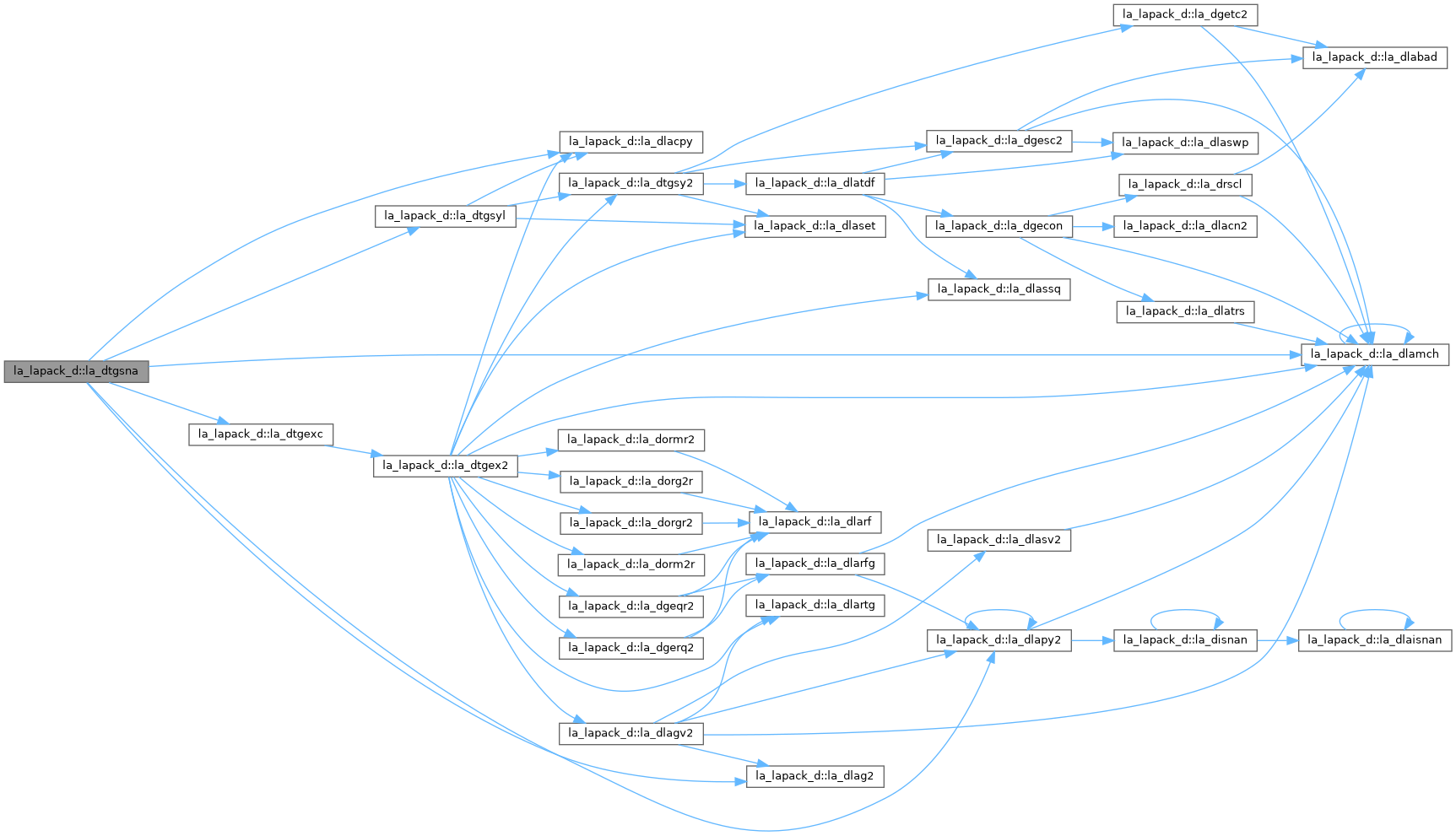
la_dtgsy2()

pure subroutine, public la_lapack_d::la_dtgsy2	(	character, intent(in)	trans,
		integer(ilp), intent(in)	ijob,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(ldd,*), intent(in)	d,
		integer(ilp), intent(in)	ldd,
		real(dp), dimension(lde,*), intent(in)	e,
		integer(ilp), intent(in)	lde,
		real(dp), dimension(ldf,*), intent(inout)	f,
		integer(ilp), intent(in)	ldf,
		real(dp), intent(out)	scale,
		real(dp), intent(inout)	rdsum,
		real(dp), intent(inout)	rdscal,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	pq,
		integer(ilp), intent(out)	info
	)

DTGSY2: solves the generalized Sylvester equation: A * R - L * B = scale * C (1) D * R - L * E = scale * F, using Level 1 and 2 BLAS. where R and L are unknown M-by-N matrices, (A, D), (B, E) and (C, F) are given matrix pairs of size M-by-M, N-by-N and M-by-N, respectively, with real entries. (A, D) and (B, E) must be in generalized Schur canonical form, i.e. A, B are upper quasi triangular and D, E are upper triangular. The solution (R, L) overwrites (C, F). 0 <= SCALE <= 1 is an output scaling factor chosen to avoid overflow. In matrix notation solving equation (1) corresponds to solve Z*x = scale*b, where Z is defined as Z = [ kron(In, A) -kron(B**T, Im) ] (2) [ kron(In, D) -kron(E**T, Im) ], Ik is the identity matrix of size k and X**T is the transpose of X. kron(X, Y) is the Kronecker product between the matrices X and Y. In the process of solving (1), we solve a number of such systems where Dim(In), Dim(In) = 1 or 2. If TRANS = 'T', solve the transposed system Z**T*y = scale*b for y, which is equivalent to solve for R and L in A**T * R + D**T * L = scale * C (3) R * B**T + L * E**T = scale * -F This case is used to compute an estimate of Dif[(A, D), (B, E)] = sigma_min(Z) using reverse communication with DLACON. DTGSY2 also (IJOB >= 1) contributes to the computation in DTGSYL of an upper bound on the separation between to matrix pairs. Then the input (A, D), (B, E) are sub-pencils of the matrix pair in DTGSYL. See DTGSYL for details.

Here is the call graph for this function:

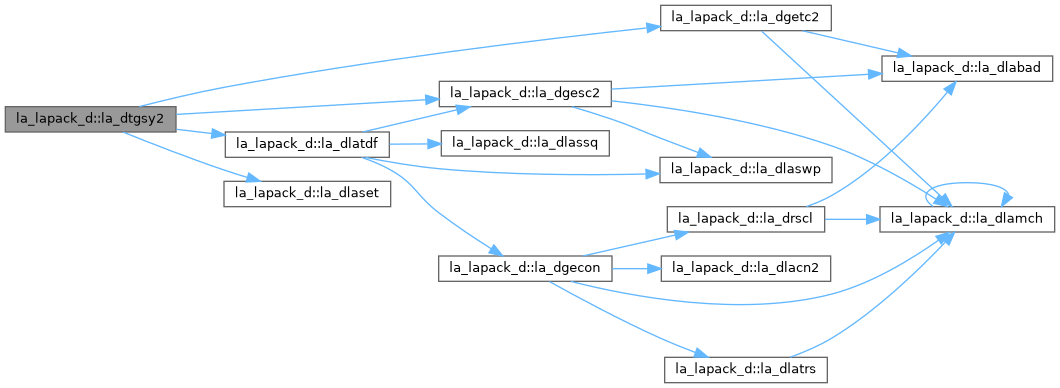
la_dtgsyl()

pure subroutine, public la_lapack_d::la_dtgsyl	(	character, intent(in)	trans,
		integer(ilp), intent(in)	ijob,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(ldd,*), intent(in)	d,
		integer(ilp), intent(in)	ldd,
		real(dp), dimension(lde,*), intent(in)	e,
		integer(ilp), intent(in)	lde,
		real(dp), dimension(ldf,*), intent(inout)	f,
		integer(ilp), intent(in)	ldf,
		real(dp), intent(out)	scale,
		real(dp), intent(out)	dif,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DTGSYL: solves the generalized Sylvester equation: A * R - L * B = scale * C (1) D * R - L * E = scale * F where R and L are unknown m-by-n matrices, (A, D), (B, E) and (C, F) are given matrix pairs of size m-by-m, n-by-n and m-by-n, respectively, with real entries. (A, D) and (B, E) must be in generalized (real) Schur canonical form, i.e. A, B are upper quasi triangular and D, E are upper triangular. The solution (R, L) overwrites (C, F). 0 <= SCALE <= 1 is an output scaling factor chosen to avoid overflow. In matrix notation (1) is equivalent to solve Zx = scale b, where Z is defined as Z = [ kron(In, A) -kron(B**T, Im) ] (2) [ kron(In, D) -kron(E**T, Im) ]. Here Ik is the identity matrix of size k and X**T is the transpose of X. kron(X, Y) is the Kronecker product between the matrices X and Y. If TRANS = 'T', DTGSYL solves the transposed system Z**T*y = scale*b, which is equivalent to solve for R and L in A**T * R + D**T * L = scale * C (3) R * B**T + L * E**T = scale * -F This case (TRANS = 'T') is used to compute an one-norm-based estimate of Dif[(A,D), (B,E)], the separation between the matrix pairs (A,D) and (B,E), using DLACON. If IJOB >= 1, DTGSYL computes a Frobenius norm-based estimate of Dif[(A,D),(B,E)]. That is, the reciprocal of a lower bound on the reciprocal of the smallest singular value of Z. See [1-2] for more information. This is a level 3 BLAS algorithm.

Here is the call graph for this function:

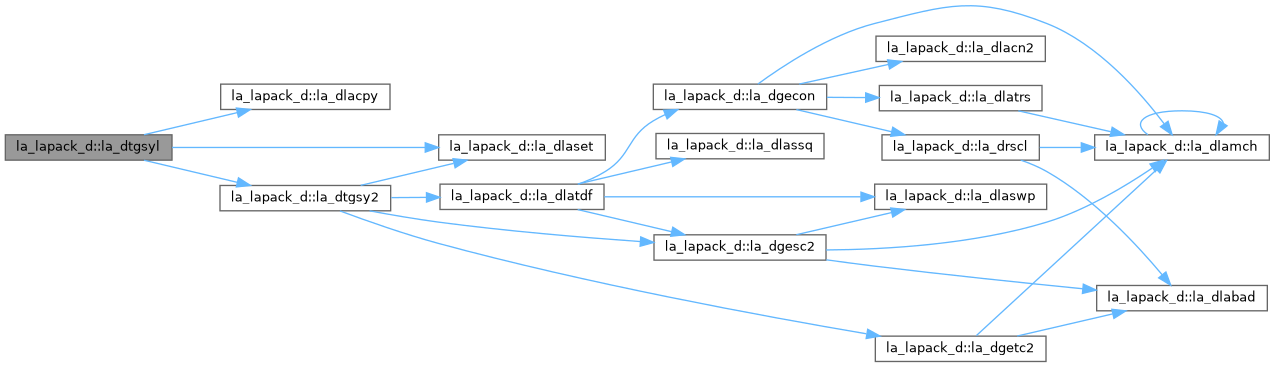
la_dtpcon()

subroutine, public la_lapack_d::la_dtpcon	(	character, intent(in)	norm,
		character, intent(in)	uplo,
		character, intent(in)	diag,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(in)	ap,
		real(dp), intent(out)	rcond,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DTPCON: estimates the reciprocal of the condition number of a packed triangular matrix A, in either the 1-norm or the infinity-norm. The norm of A is computed and an estimate is obtained for norm(inv(A)), then the reciprocal of the condition number is computed as RCOND = 1 / ( norm(A) * norm(inv(A)) ).

Here is the call graph for this function:

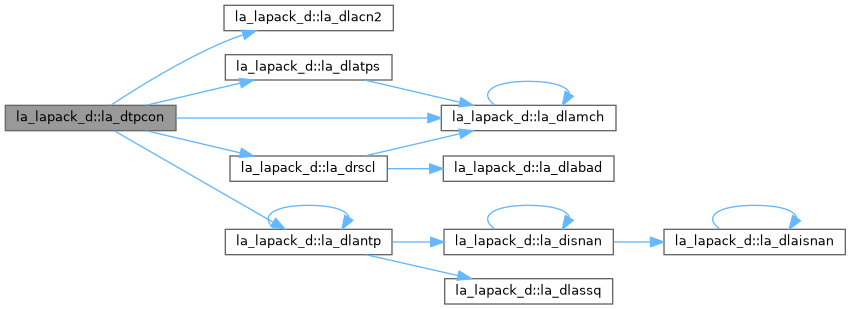
la_dtplqt()

pure subroutine, public la_lapack_d::la_dtplqt	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	l,
		integer(ilp), intent(in)	mb,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldt,*), intent(out)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DTPLQT: computes a blocked LQ factorization of a real "triangular-pentagonal" matrix C, which is composed of a triangular block A and pentagonal block B, using the compact WY representation for Q.

Here is the call graph for this function:

la_dtplqt2()

pure subroutine, public la_lapack_d::la_dtplqt2	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	l,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldt,*), intent(out)	t,
		integer(ilp), intent(in)	ldt,
		integer(ilp), intent(out)	info
	)

DTPLQT2: computes a LQ a factorization of a real "triangular-pentagonal" matrix C, which is composed of a triangular block A and pentagonal block B, using the compact WY representation for Q.

Here is the call graph for this function:

la_dtpmlqt()

pure subroutine, public la_lapack_d::la_dtpmlqt	(	character, intent(in)	side,
		character, intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		integer(ilp), intent(in)	l,
		integer(ilp), intent(in)	mb,
		real(dp), dimension(ldv,*), intent(in)	v,
		integer(ilp), intent(in)	ldv,
		real(dp), dimension(ldt,*), intent(in)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DTPMQRT applies a real orthogonal matrix Q obtained from a "triangular-pentagonal" real block reflector H to a general real matrix C, which consists of two blocks A and B.

Here is the call graph for this function:

la_dtpmqrt()

pure subroutine, public la_lapack_d::la_dtpmqrt	(	character, intent(in)	side,
		character, intent(in)	trans,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		integer(ilp), intent(in)	l,
		integer(ilp), intent(in)	nb,
		real(dp), dimension(ldv,*), intent(in)	v,
		integer(ilp), intent(in)	ldv,
		real(dp), dimension(ldt,*), intent(in)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DTPMQRT: applies a real orthogonal matrix Q obtained from a "triangular-pentagonal" real block reflector H to a general real matrix C, which consists of two blocks A and B.

Here is the call graph for this function:

la_dtpqrt()

pure subroutine, public la_lapack_d::la_dtpqrt	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	l,
		integer(ilp), intent(in)	nb,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldt,*), intent(out)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DTPQRT: computes a blocked QR factorization of a real "triangular-pentagonal" matrix C, which is composed of a triangular block A and pentagonal block B, using the compact WY representation for Q.

Here is the call graph for this function:

la_dtpqrt2()

pure subroutine, public la_lapack_d::la_dtpqrt2	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	l,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldt,*), intent(out)	t,
		integer(ilp), intent(in)	ldt,
		integer(ilp), intent(out)	info
	)

DTPQRT2: computes a QR factorization of a real "triangular-pentagonal" matrix C, which is composed of a triangular block A and pentagonal block B, using the compact WY representation for Q.

Here is the call graph for this function:

la_dtprfb()

pure subroutine, public la_lapack_d::la_dtprfb	(	character, intent(in)	side,
		character, intent(in)	trans,
		character, intent(in)	direct,
		character, intent(in)	storev,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	k,
		integer(ilp), intent(in)	l,
		real(dp), dimension(ldv,*), intent(in)	v,
		integer(ilp), intent(in)	ldv,
		real(dp), dimension(ldt,*), intent(in)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldwork,*), intent(out)	work,
		integer(ilp), intent(in)	ldwork
	)

DTPRFB: applies a real "triangular-pentagonal" block reflector H or its transpose H**T to a real matrix C, which is composed of two blocks A and B, either from the left or right.

la_dtprfs()

pure subroutine, public la_lapack_d::la_dtprfs	(	character, intent(in)	uplo,
		character, intent(in)	trans,
		character, intent(in)	diag,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(*), intent(in)	ap,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldx,*), intent(in)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), dimension(*), intent(out)	ferr,
		real(dp), dimension(*), intent(out)	berr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DTPRFS: provides error bounds and backward error estimates for the solution to a system of linear equations with a triangular packed coefficient matrix. The solution matrix X must be computed by DTPTRS or some other means before entering this routine. DTPRFS does not do iterative refinement because doing so cannot improve the backward error.

Here is the call graph for this function:

la_dtptri()

pure subroutine, public la_lapack_d::la_dtptri	(	character, intent(in)	uplo,
		character, intent(in)	diag,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(inout)	ap,
		integer(ilp), intent(out)	info
	)

DTPTRI: computes the inverse of a real upper or lower triangular matrix A stored in packed format.

la_dtptrs()

pure subroutine, public la_lapack_d::la_dtptrs	(	character, intent(in)	uplo,
		character, intent(in)	trans,
		character, intent(in)	diag,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(*), intent(in)	ap,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	info
	)

DTPTRS: solves a triangular system of the form A * X = B or A**T * X = B, where A is a triangular matrix of order N stored in packed format, and B is an N-by-NRHS matrix. A check is made to verify that A is nonsingular.

la_dtpttf()

pure subroutine, public la_lapack_d::la_dtpttf	(	character, intent(in)	transr,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(0:*), intent(in)	ap,
		real(dp), dimension(0:*), intent(out)	arf,
		integer(ilp), intent(out)	info
	)

DTPTTF: copies a triangular matrix A from standard packed format (TP) to rectangular full packed format (TF).

la_dtpttr()

pure subroutine, public la_lapack_d::la_dtpttr	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(*), intent(in)	ap,
		real(dp), dimension(lda,*), intent(out)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), intent(out)	info
	)

DTPTTR: copies a triangular matrix A from standard packed format (TP) to standard full format (TR).

la_dtrcon()

subroutine, public la_lapack_d::la_dtrcon	(	character, intent(in)	norm,
		character, intent(in)	uplo,
		character, intent(in)	diag,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), intent(out)	rcond,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DTRCON: estimates the reciprocal of the condition number of a triangular matrix A, in either the 1-norm or the infinity-norm. The norm of A is computed and an estimate is obtained for norm(inv(A)), then the reciprocal of the condition number is computed as RCOND = 1 / ( norm(A) * norm(inv(A)) ).

Here is the call graph for this function:

la_dtrevc()

pure subroutine, public la_lapack_d::la_dtrevc	(	character, intent(in)	side,
		character, intent(in)	howmny,
		logical(lk), dimension(*), intent(inout)	select,
		integer(ilp), intent(in)	n,
		real(dp), dimension(ldt,*), intent(in)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(ldvl,*), intent(inout)	vl,
		integer(ilp), intent(in)	ldvl,
		real(dp), dimension(ldvr,*), intent(inout)	vr,
		integer(ilp), intent(in)	ldvr,
		integer(ilp), intent(in)	mm,
		integer(ilp), intent(out)	m,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DTREVC: computes some or all of the right and/or left eigenvectors of a real upper quasi-triangular matrix T. Matrices of this type are produced by the Schur factorization of a real general matrix: A = Q*T*Q**T, as computed by DHSEQR. The right eigenvector x and the left eigenvector y of T corresponding to an eigenvalue w are defined by: T*x = w*x, (y**H)*T = w*(y**H) where y**H denotes the conjugate transpose of y. The eigenvalues are not input to this routine, but are read directly from the diagonal blocks of T. This routine returns the matrices X and/or Y of right and left eigenvectors of T, or the products Q*X and/or Q*Y, where Q is an input matrix. If Q is the orthogonal factor that reduces a matrix A to Schur form T, then Q*X and Q*Y are the matrices of right and left eigenvectors of A.

Here is the call graph for this function:

la_dtrevc3()

pure subroutine, public la_lapack_d::la_dtrevc3	(	character, intent(in)	side,
		character, intent(in)	howmny,
		logical(lk), dimension(*), intent(inout)	select,
		integer(ilp), intent(in)	n,
		real(dp), dimension(ldt,*), intent(in)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(ldvl,*), intent(inout)	vl,
		integer(ilp), intent(in)	ldvl,
		real(dp), dimension(ldvr,*), intent(inout)	vr,
		integer(ilp), intent(in)	ldvr,
		integer(ilp), intent(in)	mm,
		integer(ilp), intent(out)	m,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DTREVC3: computes some or all of the right and/or left eigenvectors of a real upper quasi-triangular matrix T. Matrices of this type are produced by the Schur factorization of a real general matrix: A = Q*T*Q**T, as computed by DHSEQR. The right eigenvector x and the left eigenvector y of T corresponding to an eigenvalue w are defined by: T*x = w*x, (y**T)*T = w*(y**T) where y**T denotes the transpose of the vector y. The eigenvalues are not input to this routine, but are read directly from the diagonal blocks of T. This routine returns the matrices X and/or Y of right and left eigenvectors of T, or the products Q*X and/or Q*Y, where Q is an input matrix. If Q is the orthogonal factor that reduces a matrix A to Schur form T, then Q*X and Q*Y are the matrices of right and left eigenvectors of A. This uses a Level 3 BLAS version of the back transformation.

Here is the call graph for this function:

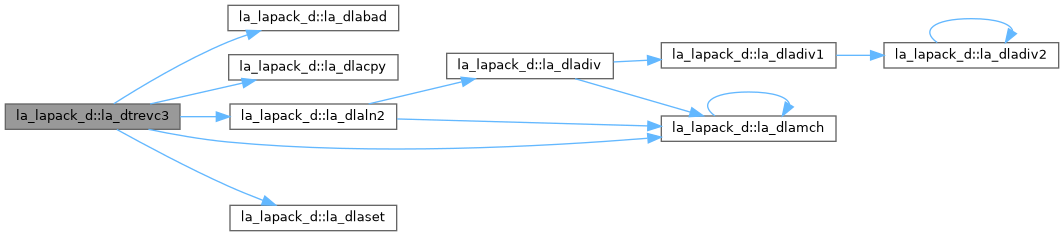
la_dtrexc()

subroutine, public la_lapack_d::la_dtrexc	(	character, intent(in)	compq,
		integer(ilp), intent(in)	n,
		real(dp), dimension(ldt,*), intent(inout)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(ldq,*), intent(inout)	q,
		integer(ilp), intent(in)	ldq,
		integer(ilp), intent(inout)	ifst,
		integer(ilp), intent(inout)	ilst,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

DTREXC: reorders the real Schur factorization of a real matrix A = Q*T*Q**T, so that the diagonal block of T with row index IFST is moved to row ILST. The real Schur form T is reordered by an orthogonal similarity transformation Z**T*T*Z, and optionally the matrix Q of Schur vectors is updated by postmultiplying it with Z. T must be in Schur canonical form (as returned by DHSEQR), that is, block upper triangular with 1-by-1 and 2-by-2 diagonal blocks; each 2-by-2 diagonal block has its diagonal elements equal and its off-diagonal elements of opposite sign.

Here is the call graph for this function:

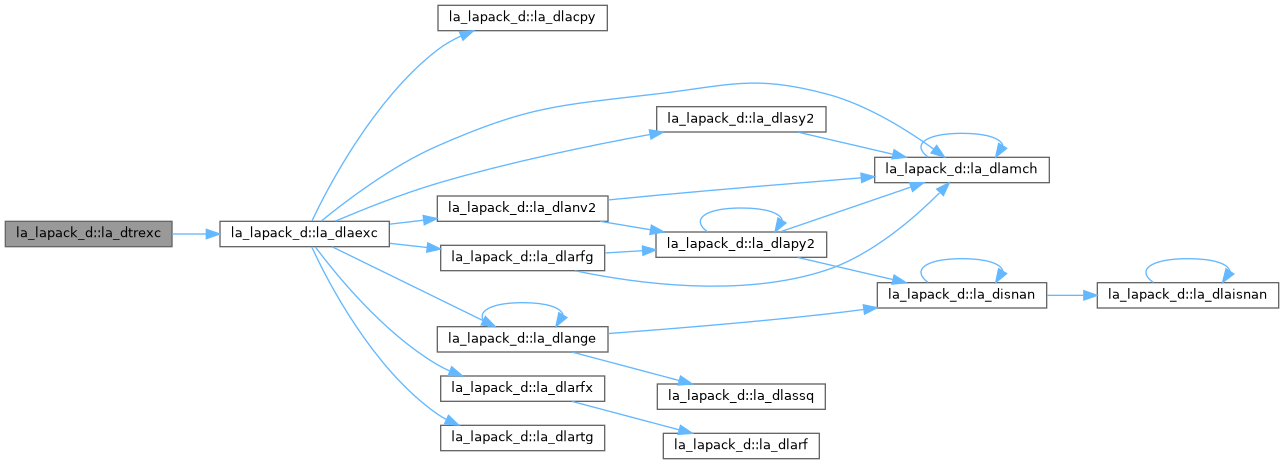
la_dtrrfs()

pure subroutine, public la_lapack_d::la_dtrrfs	(	character, intent(in)	uplo,
		character, intent(in)	trans,
		character, intent(in)	diag,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldx,*), intent(in)	x,
		integer(ilp), intent(in)	ldx,
		real(dp), dimension(*), intent(out)	ferr,
		real(dp), dimension(*), intent(out)	berr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DTRRFS: provides error bounds and backward error estimates for the solution to a system of linear equations with a triangular coefficient matrix. The solution matrix X must be computed by DTRTRS or some other means before entering this routine. DTRRFS does not do iterative refinement because doing so cannot improve the backward error.

Here is the call graph for this function:

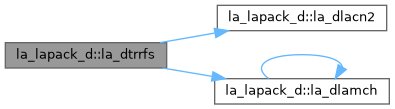
la_dtrsen()

subroutine, public la_lapack_d::la_dtrsen	(	character, intent(in)	job,
		character, intent(in)	compq,
		logical(lk), dimension(*), intent(in)	select,
		integer(ilp), intent(in)	n,
		real(dp), dimension(ldt,*), intent(inout)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(ldq,*), intent(inout)	q,
		integer(ilp), intent(in)	ldq,
		real(dp), dimension(*), intent(out)	wr,
		real(dp), dimension(*), intent(out)	wi,
		integer(ilp), intent(out)	m,
		real(dp), intent(out)	s,
		real(dp), intent(out)	sep,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(in)	liwork,
		integer(ilp), intent(out)	info
	)

DTRSEN: reorders the real Schur factorization of a real matrix A = Q*T*Q**T, so that a selected cluster of eigenvalues appears in the leading diagonal blocks of the upper quasi-triangular matrix T, and the leading columns of Q form an orthonormal basis of the corresponding right invariant subspace. Optionally the routine computes the reciprocal condition numbers of the cluster of eigenvalues and/or the invariant subspace. T must be in Schur canonical form (as returned by DHSEQR), that is, block upper triangular with 1-by-1 and 2-by-2 diagonal blocks; each 2-by-2 diagonal block has its diagonal elements equal and its off-diagonal elements of opposite sign.

Here is the call graph for this function:

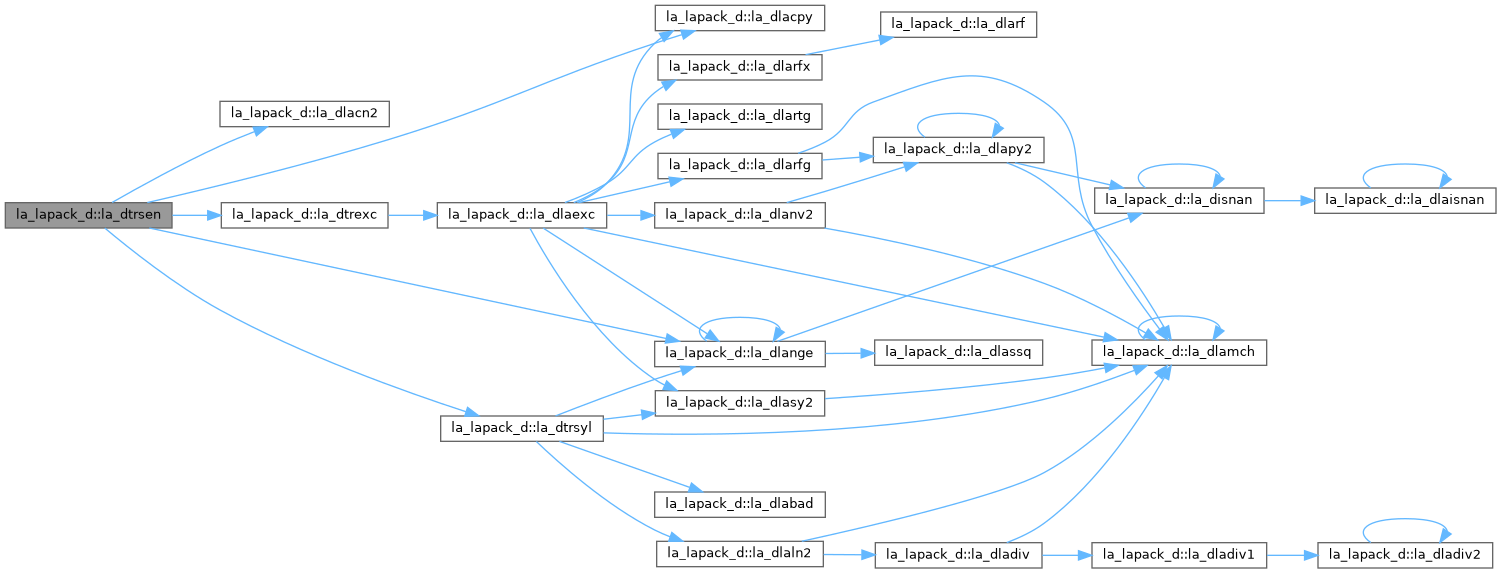
la_dtrsna()

subroutine, public la_lapack_d::la_dtrsna	(	character, intent(in)	job,
		character, intent(in)	howmny,
		logical(lk), dimension(*), intent(in)	select,
		integer(ilp), intent(in)	n,
		real(dp), dimension(ldt,*), intent(in)	t,
		integer(ilp), intent(in)	ldt,
		real(dp), dimension(ldvl,*), intent(in)	vl,
		integer(ilp), intent(in)	ldvl,
		real(dp), dimension(ldvr,*), intent(in)	vr,
		integer(ilp), intent(in)	ldvr,
		real(dp), dimension(*), intent(out)	s,
		real(dp), dimension(*), intent(out)	sep,
		integer(ilp), intent(in)	mm,
		integer(ilp), intent(out)	m,
		real(dp), dimension(ldwork,*), intent(out)	work,
		integer(ilp), intent(in)	ldwork,
		integer(ilp), dimension(*), intent(out)	iwork,
		integer(ilp), intent(out)	info
	)

DTRSNA: estimates reciprocal condition numbers for specified eigenvalues and/or right eigenvectors of a real upper quasi-triangular matrix T (or of any matrix Q*T*Q**T with Q orthogonal). T must be in Schur canonical form (as returned by DHSEQR), that is, block upper triangular with 1-by-1 and 2-by-2 diagonal blocks; each 2-by-2 diagonal block has its diagonal elements equal and its off-diagonal elements of opposite sign.

Here is the call graph for this function:

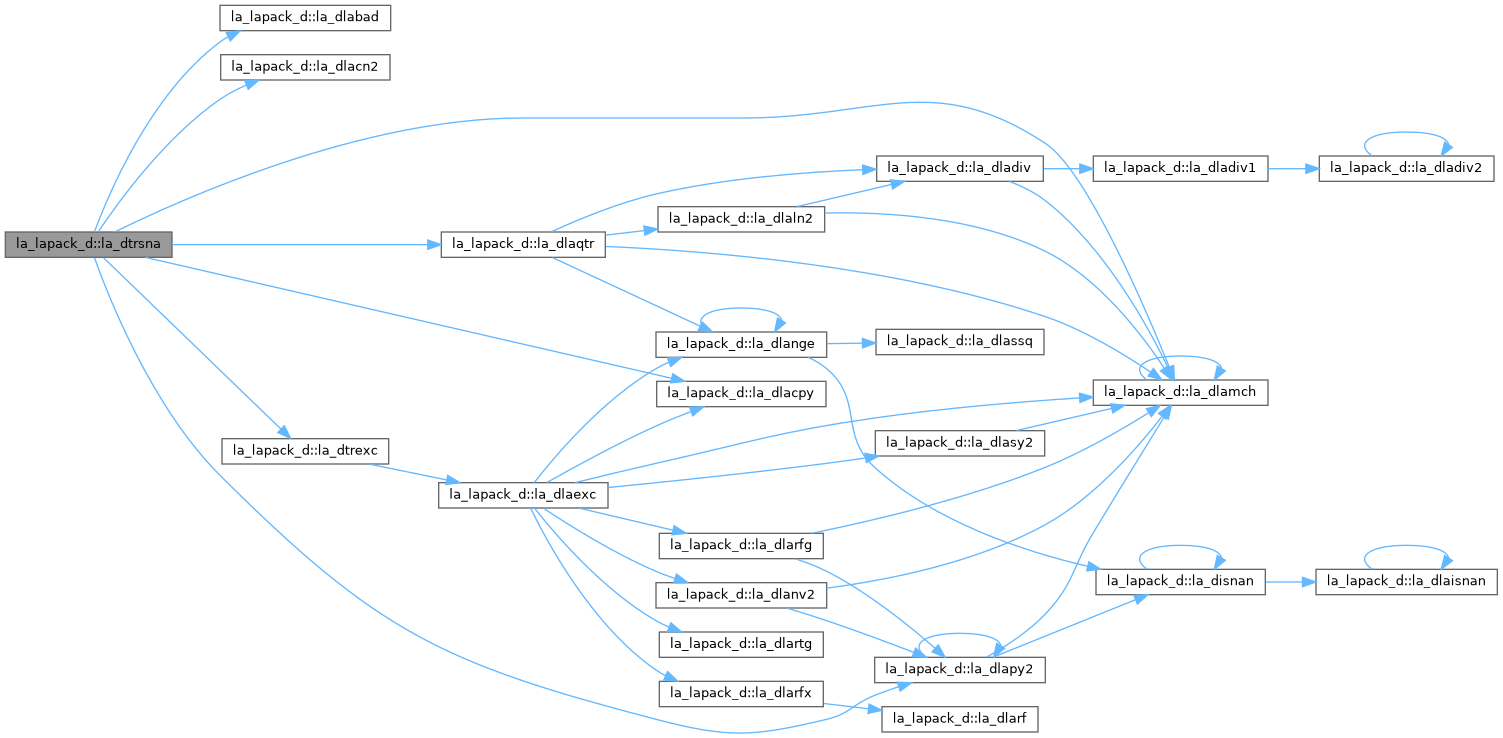
la_dtrsyl()

subroutine, public la_lapack_d::la_dtrsyl	(	character, intent(in)	trana,
		character, intent(in)	tranb,
		integer(ilp), intent(in)	isgn,
		integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(in)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), intent(out)	scale,
		integer(ilp), intent(out)	info
	)

DTRSYL: solves the real Sylvester matrix equation: op(A)*X + X*op(B) = scale*C or op(A)*X - X*op(B) = scale*C, where op(A) = A or A**T, and A and B are both upper quasi- triangular. A is M-by-M and B is N-by-N; the right hand side C and the solution X are M-by-N; and scale is an output scale factor, set <= 1 to avoid overflow in X. A and B must be in Schur canonical form (as returned by DHSEQR), that is, block upper triangular with 1-by-1 and 2-by-2 diagonal blocks; each 2-by-2 diagonal block has its diagonal elements equal and its off-diagonal elements of opposite sign.

Here is the call graph for this function:

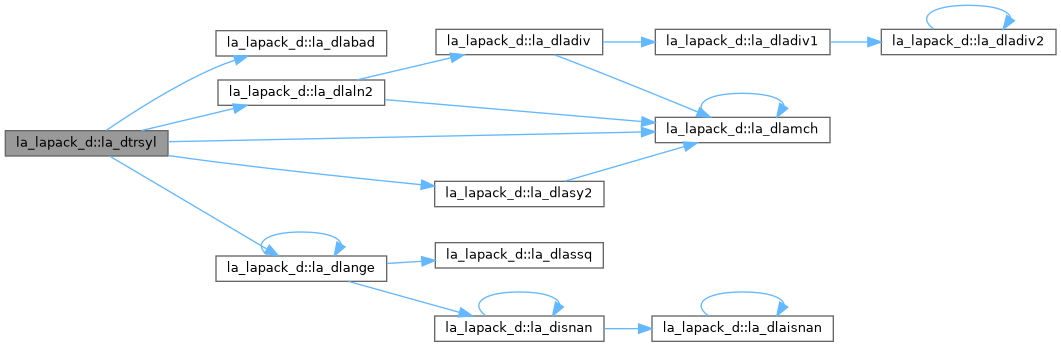
la_dtrti2()

pure subroutine, public la_lapack_d::la_dtrti2	(	character, intent(in)	uplo,
		character, intent(in)	diag,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), intent(out)	info
	)

DTRTI2: computes the inverse of a real upper or lower triangular matrix. This is the Level 2 BLAS version of the algorithm.

la_dtrtri()

pure subroutine, public la_lapack_d::la_dtrtri	(	character, intent(in)	uplo,
		character, intent(in)	diag,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), intent(out)	info
	)

DTRTRI: computes the inverse of a real upper or lower triangular matrix A. This is the Level 3 BLAS version of the algorithm.

Here is the call graph for this function:

la_dtrtrs()

pure subroutine, public la_lapack_d::la_dtrtrs	(	character, intent(in)	uplo,
		character, intent(in)	trans,
		character, intent(in)	diag,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	nrhs,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	info
	)

DTRTRS: solves a triangular system of the form A * X = B or A**T * X = B, where A is a triangular matrix of order N, and B is an N-by-NRHS matrix. A check is made to verify that A is nonsingular.

la_dtrttf()

pure subroutine, public la_lapack_d::la_dtrttf	(	character, intent(in)	transr,
		character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(0:lda - 1,0:*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(0:*), intent(out)	arf,
		integer(ilp), intent(out)	info
	)

DTRTTF: copies a triangular matrix A from standard full format (TR) to rectangular full packed format (TF) .

la_dtrttp()

pure subroutine, public la_lapack_d::la_dtrttp	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(in)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	ap,
		integer(ilp), intent(out)	info
	)

DTRTTP: copies a triangular matrix A from full format (TR) to standard packed format (TP).

la_dtzrzf()

pure subroutine, public la_lapack_d::la_dtzrzf	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	tau,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

DTZRZF: reduces the M-by-N ( M<=N ) real upper trapezoidal matrix A to upper triangular form by means of orthogonal transformations. The upper trapezoidal matrix A is factored as A = ( R 0 ) * Z, where Z is an N-by-N orthogonal matrix and R is an M-by-M upper triangular matrix.

Here is the call graph for this function:

la_dzsum1()

pure real(dp) function, public la_lapack_d::la_dzsum1	(	integer(ilp), intent(in)	n,
		complex(dp), dimension(*), intent(in)	cx,
		integer(ilp), intent(in)	incx
	)

DZSUM1: takes the sum of the absolute values of a complex vector and returns a double precision result. Based on DZASUM from the Level 1 BLAS. The change is to use the 'genuine' absolute value.

Here is the call graph for this function: