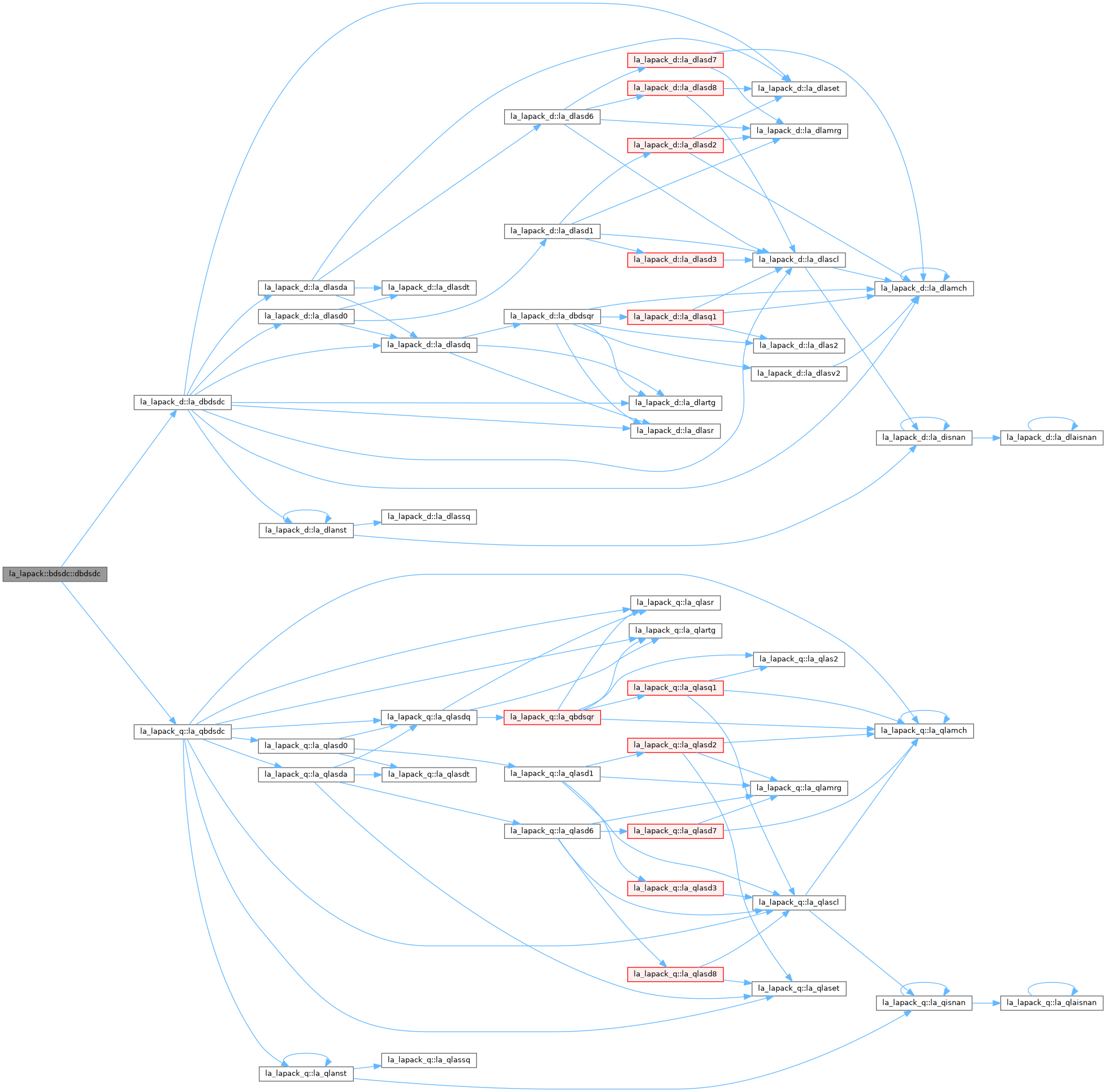
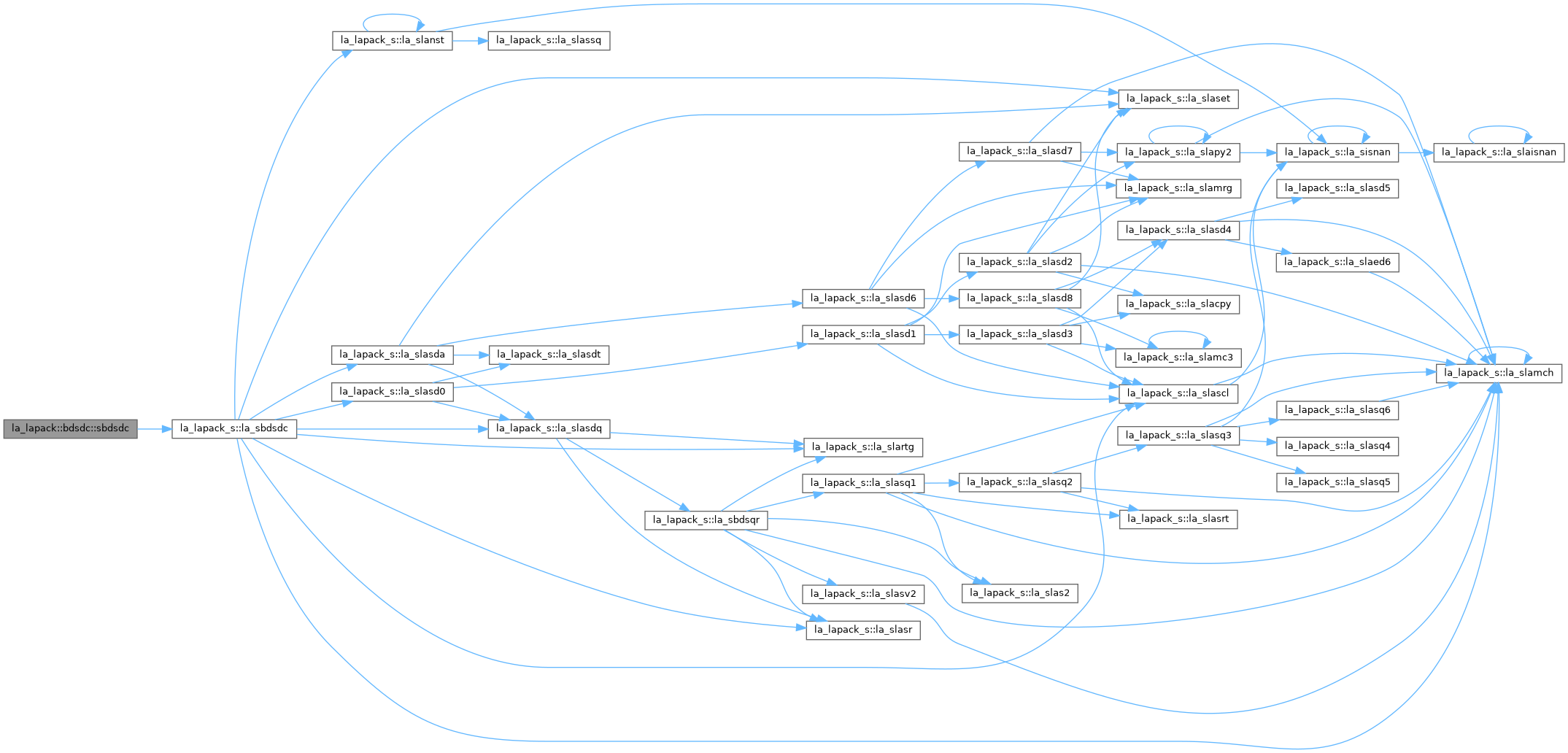
BDSDC: computes the singular value decomposition (SVD) of a real N-by-N (upper or lower) bidiagonal matrix B: B = U * S * VT, using a divide and conquer method, where S is a diagonal matrix with non-negative diagonal elements (the singular values of B), and U and VT are orthogonal matrices of left and right singular vectors, respectively. BDSDC can be used to compute all singular values, and optionally, singular vectors or singular vectors in compact form. This code makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none. See DLASD3 for details. The code currently calls DLASDQ if singular values only are desired. However, it can be slightly modified to compute singular values using the divide and conquer method.
More...
|
| pure subroutine | dbdsdc (uplo, compq, n, d, e, u, ldu, vt, ldvt, q, iq, work, iwork, info) |
| |
| | la_dbdsdc |
| |
| | la_qbdsdc |
| |
| pure subroutine | sbdsdc (uplo, compq, n, d, e, u, ldu, vt, ldvt, q, iq, work, iwork, info) |
| |
| | la_sbdsdc |
| |
BDSDC: computes the singular value decomposition (SVD) of a real N-by-N (upper or lower) bidiagonal matrix B: B = U * S * VT, using a divide and conquer method, where S is a diagonal matrix with non-negative diagonal elements (the singular values of B), and U and VT are orthogonal matrices of left and right singular vectors, respectively. BDSDC can be used to compute all singular values, and optionally, singular vectors or singular vectors in compact form. This code makes very mild assumptions about floating point arithmetic. It will work on machines with a guard digit in add/subtract, or on those binary machines without guard digits which subtract like the Cray X-MP, Cray Y-MP, Cray C-90, or Cray-2. It could conceivably fail on hexadecimal or decimal machines without guard digits, but we know of none. See DLASD3 for details. The code currently calls DLASDQ if singular values only are desired. However, it can be slightly modified to compute singular values using the divide and conquer method.
◆ dbdsdc()
| pure subroutine la_lapack::bdsdc::dbdsdc |
( |
character, intent(in) | uplo, |
|
|
character, intent(in) | compq, |
|
|
integer(ilp), intent(in) | n, |
|
|
real(dp), dimension(*), intent(inout) | d, |
|
|
real(dp), dimension(*), intent(inout) | e, |
|
|
real(dp), dimension(ldu,*), intent(out) | u, |
|
|
integer(ilp), intent(in) | ldu, |
|
|
real(dp), dimension(ldvt,*), intent(out) | vt, |
|
|
integer(ilp), intent(in) | ldvt, |
|
|
real(dp), dimension(*), intent(out) | q, |
|
|
integer(ilp), dimension(*), intent(out) | iq, |
|
|
real(dp), dimension(*), intent(out) | work, |
|
|
integer(ilp), dimension(*), intent(out) | iwork, |
|
|
integer(ilp), intent(out) | info ) |
◆ la_dbdsdc()
| la_lapack::bdsdc::la_dbdsdc |
◆ la_qbdsdc()
| la_lapack::bdsdc::la_qbdsdc |
◆ la_sbdsdc()
| la_lapack::bdsdc::la_sbdsdc |
◆ sbdsdc()
| pure subroutine la_lapack::bdsdc::sbdsdc |
( |
character, intent(in) | uplo, |
|
|
character, intent(in) | compq, |
|
|
integer(ilp), intent(in) | n, |
|
|
real(sp), dimension(*), intent(inout) | d, |
|
|
real(sp), dimension(*), intent(inout) | e, |
|
|
real(sp), dimension(ldu,*), intent(out) | u, |
|
|
integer(ilp), intent(in) | ldu, |
|
|
real(sp), dimension(ldvt,*), intent(out) | vt, |
|
|
integer(ilp), intent(in) | ldvt, |
|
|
real(sp), dimension(*), intent(out) | q, |
|
|
integer(ilp), dimension(*), intent(out) | iq, |
|
|
real(sp), dimension(*), intent(out) | work, |
|
|
integer(ilp), dimension(*), intent(out) | iwork, |
|
|
integer(ilp), intent(out) | info ) |
The documentation for this interface was generated from the following file: