la_lapack::gglse Interface Reference

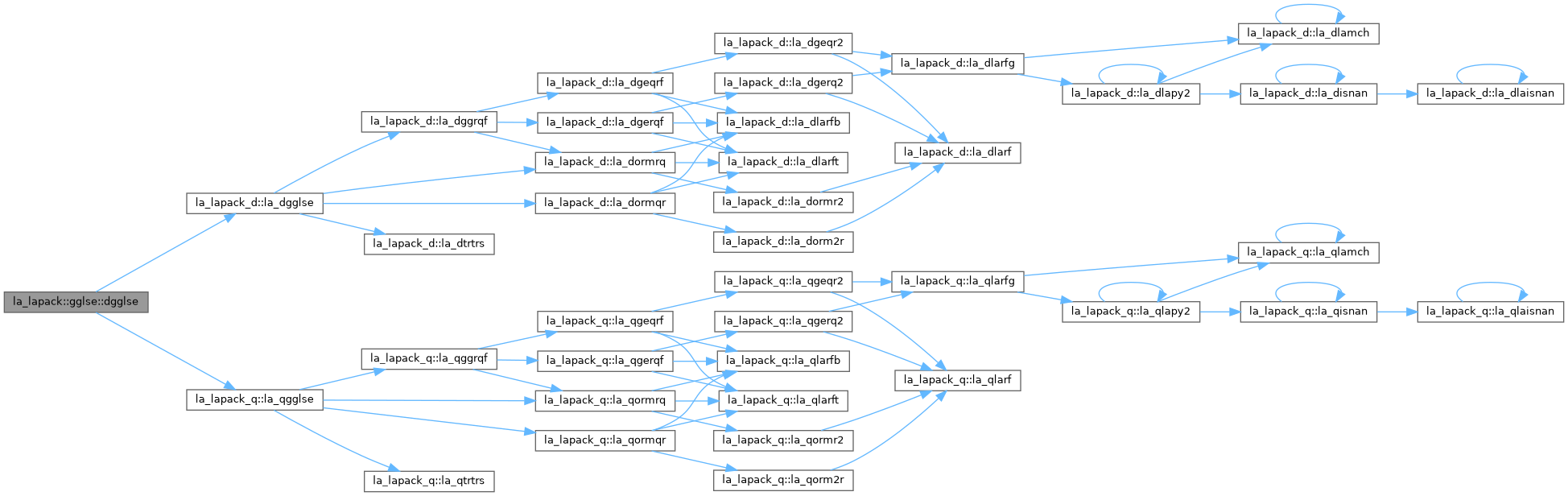
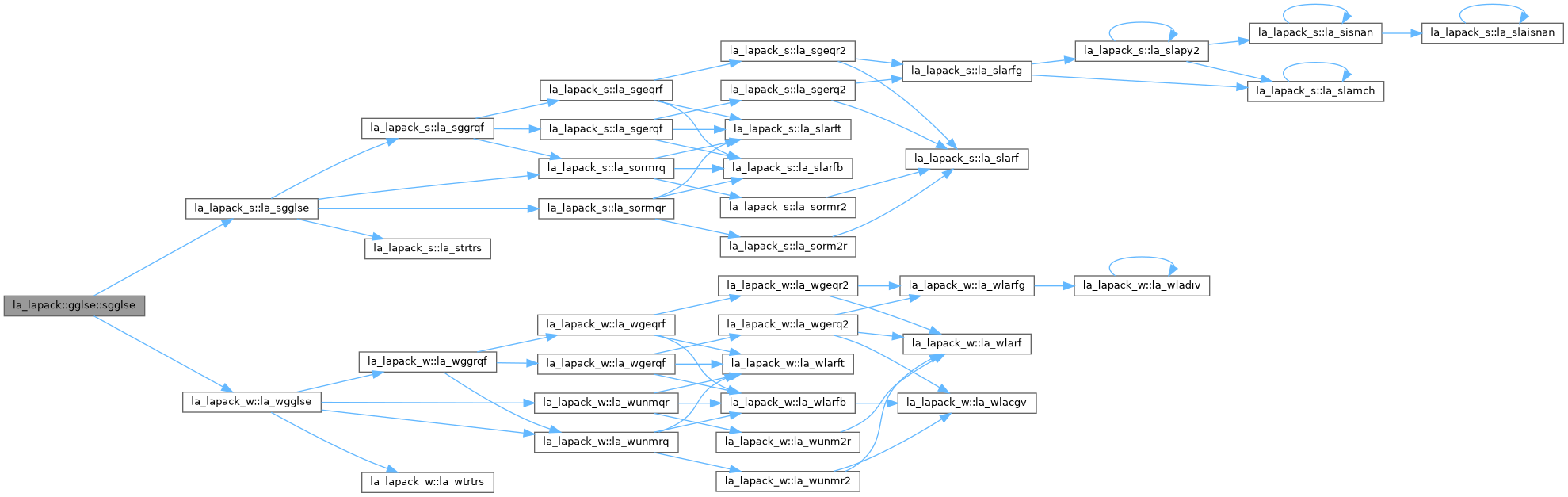
GGLSE: solves the linear equality-constrained least squares (LSE) problem: minimize || c - A*x ||_2 subject to B*x = d where A is an M-by-N matrix, B is a P-by-N matrix, c is a given M-vector, and d is a given P-vector. It is assumed that P <= N <= M+P, and rank(B) = P and rank( (A) ) = N. ( (B) ) These conditions ensure that the LSE problem has a unique solution, which is obtained using a generalized RQ factorization of the matrices (B, A) given by B = (0 R)*Q, A = Z*T*Q. More...

Public Member Functions
pure subroutine	cgglse (m, n, p, a, lda, b, ldb, c, d, x, work, lwork, info)
	la_cgglse
pure subroutine	dgglse (m, n, p, a, lda, b, ldb, c, d, x, work, lwork, info)
	la_dgglse
	la_qgglse
pure subroutine	sgglse (m, n, p, a, lda, b, ldb, c, d, x, work, lwork, info)
	la_sgglse
	la_wgglse
pure subroutine	zgglse (m, n, p, a, lda, b, ldb, c, d, x, work, lwork, info)
	la_zgglse

Detailed Description

GGLSE: solves the linear equality-constrained least squares (LSE) problem: minimize || c - A*x ||_2 subject to B*x = d where A is an M-by-N matrix, B is a P-by-N matrix, c is a given M-vector, and d is a given P-vector. It is assumed that P <= N <= M+P, and rank(B) = P and rank( (A) ) = N. ( (B) ) These conditions ensure that the LSE problem has a unique solution, which is obtained using a generalized RQ factorization of the matrices (B, A) given by B = (0 R)*Q, A = Z*T*Q.

Member Function/Subroutine Documentation

cgglse()

pure subroutine la_lapack::gglse::cgglse	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	p,
		complex(sp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		complex(sp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		complex(sp), dimension(*), intent(inout)	c,
		complex(sp), dimension(*), intent(inout)	d,
		complex(sp), dimension(*), intent(out)	x,
		complex(sp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info )

Here is the call graph for this function:

dgglse()

pure subroutine la_lapack::gglse::dgglse	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	p,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(*), intent(inout)	c,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(out)	x,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info )

Here is the call graph for this function:

la_cgglse()

la_lapack::gglse::la_cgglse

la_dgglse()

la_lapack::gglse::la_dgglse

la_qgglse()

la_lapack::gglse::la_qgglse

la_sgglse()

la_lapack::gglse::la_sgglse

la_wgglse()

la_lapack::gglse::la_wgglse

la_zgglse()

la_lapack::gglse::la_zgglse

sgglse()

pure subroutine la_lapack::gglse::sgglse	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	p,
		real(sp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(sp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(sp), dimension(*), intent(inout)	c,
		real(sp), dimension(*), intent(inout)	d,
		real(sp), dimension(*), intent(out)	x,
		real(sp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info )

Here is the call graph for this function:

zgglse()

pure subroutine la_lapack::gglse::zgglse	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	p,
		complex(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		complex(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		complex(dp), dimension(*), intent(inout)	c,
		complex(dp), dimension(*), intent(inout)	d,
		complex(dp), dimension(*), intent(out)	x,
		complex(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info )

Here is the call graph for this function:

---

The documentation for this interface was generated from the following file:

• la_lapack.f90