la_lapack::ggrqf Interface Reference

GGRQF: computes a generalized RQ factorization of an M-by-N matrix A and a P-by-N matrix B: A = R*Q, B = Z*T*Q, where Q is an N-by-N unitary matrix, Z is a P-by-P unitary matrix, and R and T assume one of the forms: if M <= N, R = ( 0 R12 ) M, or if M > N, R = ( R11 ) M-N, N-M M ( R21 ) N N where R12 or R21 is upper triangular, and if P >= N, T = ( T11 ) N , or if P < N, T = ( T11 T12 ) P, ( 0 ) P-N P N-P N where T11 is upper triangular. In particular, if B is square and nonsingular, the GRQ factorization of A and B implicitly gives the RQ factorization of A*inv(B): A*inv(B) = (R*inv(T))*Z**H where inv(B) denotes the inverse of the matrix B, and Z**H denotes the conjugate transpose of the matrix Z. More...

Public Member Functions
pure subroutine	cggrqf (m, p, n, a, lda, taua, b, ldb, taub, work, lwork, info)
	la_cggrqf
pure subroutine	dggrqf (m, p, n, a, lda, taua, b, ldb, taub, work, lwork, info)
	la_dggrqf
	la_qggrqf
pure subroutine	sggrqf (m, p, n, a, lda, taua, b, ldb, taub, work, lwork, info)
	la_sggrqf
	la_wggrqf
pure subroutine	zggrqf (m, p, n, a, lda, taua, b, ldb, taub, work, lwork, info)
	la_zggrqf

Detailed Description

GGRQF: computes a generalized RQ factorization of an M-by-N matrix A and a P-by-N matrix B: A = R*Q, B = Z*T*Q, where Q is an N-by-N unitary matrix, Z is a P-by-P unitary matrix, and R and T assume one of the forms: if M <= N, R = ( 0 R12 ) M, or if M > N, R = ( R11 ) M-N, N-M M ( R21 ) N N where R12 or R21 is upper triangular, and if P >= N, T = ( T11 ) N , or if P < N, T = ( T11 T12 ) P, ( 0 ) P-N P N-P N where T11 is upper triangular. In particular, if B is square and nonsingular, the GRQ factorization of A and B implicitly gives the RQ factorization of A*inv(B): A*inv(B) = (R*inv(T))*Z**H where inv(B) denotes the inverse of the matrix B, and Z**H denotes the conjugate transpose of the matrix Z.

Member Function/Subroutine Documentation

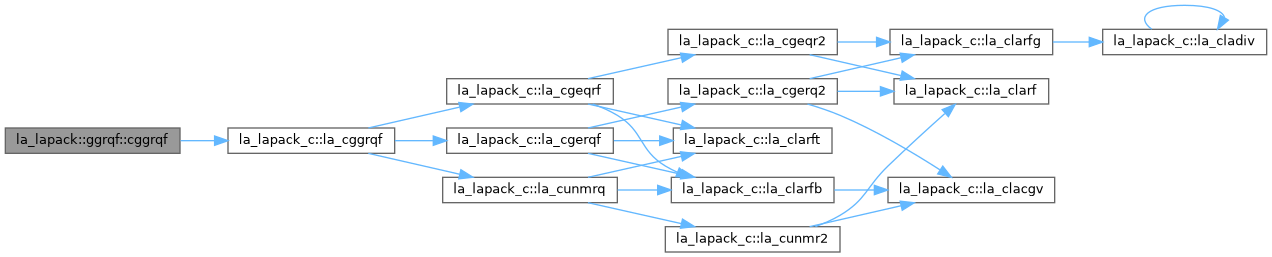
cggrqf()

pure subroutine la_lapack::ggrqf::cggrqf	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	p,
		integer(ilp), intent(in)	n,
		complex(sp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		complex(sp), dimension(*), intent(out)	taua,
		complex(sp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		complex(sp), dimension(*), intent(out)	taub,
		complex(sp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

Here is the call graph for this function:

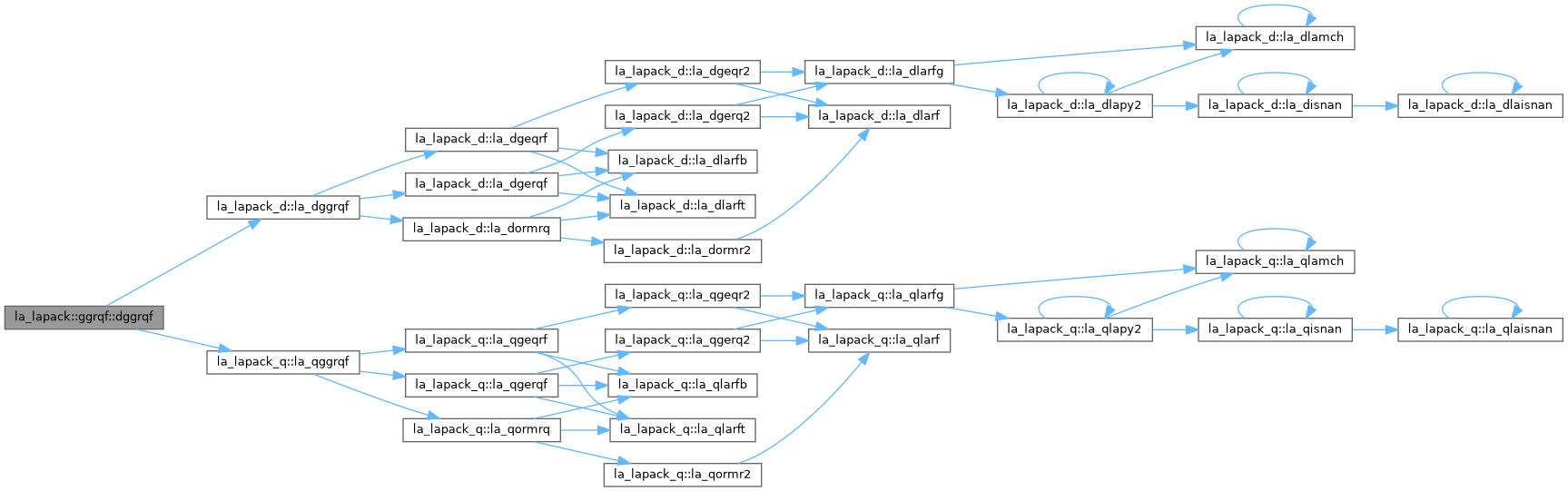
dggrqf()

pure subroutine la_lapack::ggrqf::dggrqf	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	p,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(*), intent(out)	taua,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(dp), dimension(*), intent(out)	taub,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

Here is the call graph for this function:

la_cggrqf()

la_lapack::ggrqf::la_cggrqf

la_dggrqf()

la_lapack::ggrqf::la_dggrqf

la_qggrqf()

la_lapack::ggrqf::la_qggrqf

la_sggrqf()

la_lapack::ggrqf::la_sggrqf

la_wggrqf()

la_lapack::ggrqf::la_wggrqf

la_zggrqf()

la_lapack::ggrqf::la_zggrqf

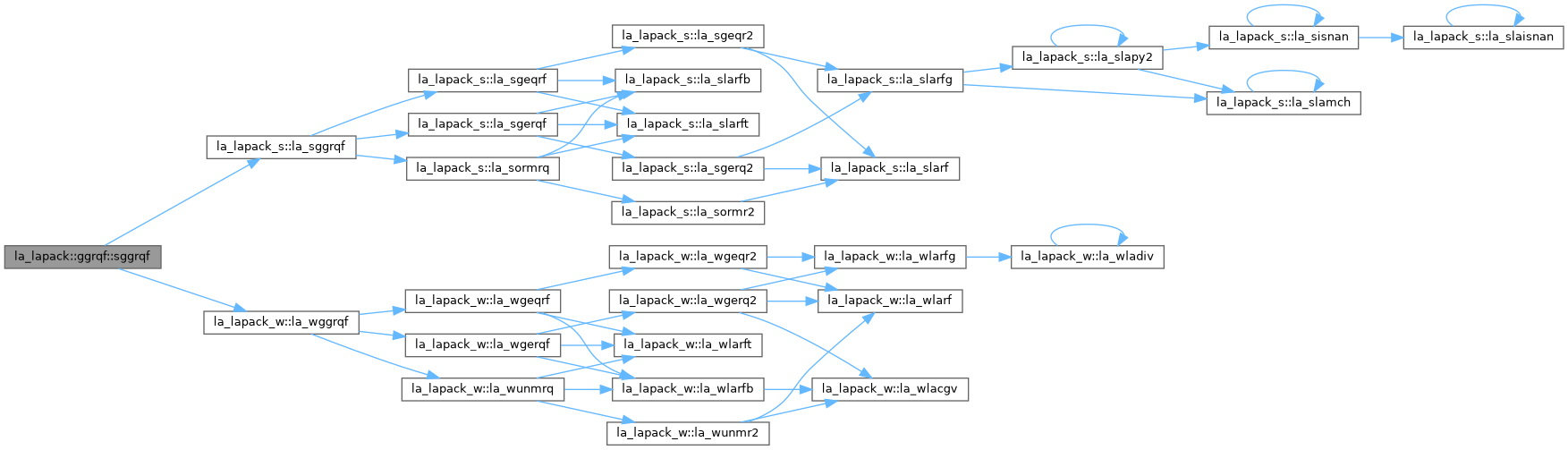
sggrqf()

pure subroutine la_lapack::ggrqf::sggrqf	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	p,
		integer(ilp), intent(in)	n,
		real(sp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(sp), dimension(*), intent(out)	taua,
		real(sp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		real(sp), dimension(*), intent(out)	taub,
		real(sp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

Here is the call graph for this function:

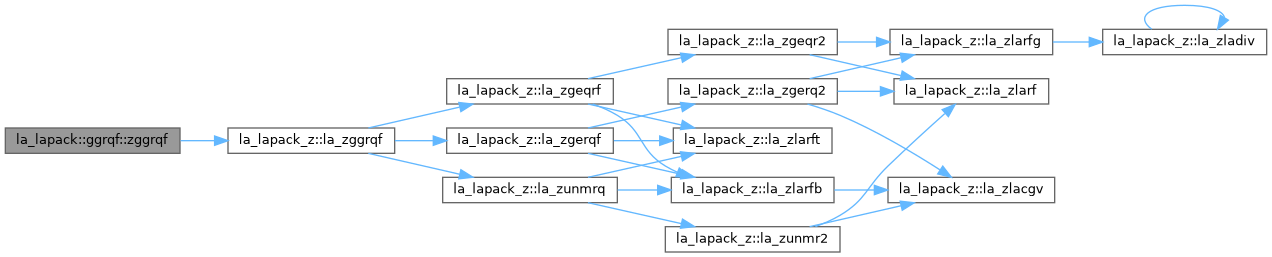
zggrqf()

pure subroutine la_lapack::ggrqf::zggrqf	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	p,
		integer(ilp), intent(in)	n,
		complex(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		complex(dp), dimension(*), intent(out)	taua,
		complex(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		complex(dp), dimension(*), intent(out)	taub,
		complex(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		integer(ilp), intent(out)	info
	)

Here is the call graph for this function:

---

The documentation for this interface was generated from the following file:

• la_lapack.f90