GSVJ1: is called from CGESVJ as a pre-processor and that is its main purpose. It applies Jacobi rotations in the same way as CGESVJ does, but it targets only particular pivots and it does not check convergence (stopping criterion). Few tuning parameters (marked by [TP]) are available for the implementer. Further Details. More...
Public Member Functions | |
| pure subroutine | cgsvj1 (jobv, m, n, n1, a, lda, d, sva, mv, v, ldv, eps, sfmin, tol, nsweep, work, lwork, info) |
| la_cgsvj1 | |
| pure subroutine | dgsvj1 (jobv, m, n, n1, a, lda, d, sva, mv, v, ldv, eps, sfmin, tol, nsweep, work, lwork, info) |
| la_dgsvj1 | |
| la_qgsvj1 | |
| pure subroutine | sgsvj1 (jobv, m, n, n1, a, lda, d, sva, mv, v, ldv, eps, sfmin, tol, nsweep, work, lwork, info) |
| la_sgsvj1 | |
| la_wgsvj1 | |
| pure subroutine | zgsvj1 (jobv, m, n, n1, a, lda, d, sva, mv, v, ldv, eps, sfmin, tol, nsweep, work, lwork, info) |
| la_zgsvj1 | |
Detailed Description
GSVJ1: is called from CGESVJ as a pre-processor and that is its main purpose. It applies Jacobi rotations in the same way as CGESVJ does, but it targets only particular pivots and it does not check convergence (stopping criterion). Few tuning parameters (marked by [TP]) are available for the implementer. Further Details.
GSVJ1 applies few sweeps of Jacobi rotations in the column space of the input M-by-N matrix A. The pivot pairs are taken from the (1,2) off-diagonal block in the corresponding N-by-N Gram matrix A^T * A. The block-entries (tiles) of the (1,2) off-diagonal block are marked by the [x]'s in the following scheme: | * * * [x] [x] [x]| | * * * [x] [x] [x]| Row-cycling in the nblr-by-nblc [x] blocks. | * * * [x] [x] [x]| Row-cyclic pivoting inside each [x] block. |[x] [x] [x] * * * | |[x] [x] [x] * * * | |[x] [x] [x] * * * | In terms of the columns of A, the first N1 columns are rotated 'against' the remaining N-N1 columns, trying to increase the angle between the corresponding subspaces. The off-diagonal block is N1-by(N-N1) and it is tiled using quadratic tiles of side KBL. Here, KBL is a tuning parameter. The number of sweeps is given in NSWEEP and the orthogonality threshold is given in TOL.
Member Function/Subroutine Documentation
◆ cgsvj1()
| pure subroutine la_lapack::gsvj1::cgsvj1 | ( | character, intent(in) | jobv, |
| integer(ilp), intent(in) | m, | ||
| integer(ilp), intent(in) | n, | ||
| integer(ilp), intent(in) | n1, | ||
| complex(sp), dimension(lda,*), intent(inout) | a, | ||
| integer(ilp), intent(in) | lda, | ||
| complex(sp), dimension(n), intent(inout) | d, | ||
| real(sp), dimension(n), intent(inout) | sva, | ||
| integer(ilp), intent(in) | mv, | ||
| complex(sp), dimension(ldv,*), intent(inout) | v, | ||
| integer(ilp), intent(in) | ldv, | ||
| real(sp), intent(in) | eps, | ||
| real(sp), intent(in) | sfmin, | ||
| real(sp), intent(in) | tol, | ||
| integer(ilp), intent(in) | nsweep, | ||
| complex(sp), dimension(lwork), intent(out) | work, | ||
| integer(ilp), intent(in) | lwork, | ||
| integer(ilp), intent(out) | info ) |

◆ dgsvj1()
| pure subroutine la_lapack::gsvj1::dgsvj1 | ( | character, intent(in) | jobv, |
| integer(ilp), intent(in) | m, | ||
| integer(ilp), intent(in) | n, | ||
| integer(ilp), intent(in) | n1, | ||
| real(dp), dimension(lda,*), intent(inout) | a, | ||
| integer(ilp), intent(in) | lda, | ||
| real(dp), dimension(n), intent(inout) | d, | ||
| real(dp), dimension(n), intent(inout) | sva, | ||
| integer(ilp), intent(in) | mv, | ||
| real(dp), dimension(ldv,*), intent(inout) | v, | ||
| integer(ilp), intent(in) | ldv, | ||
| real(dp), intent(in) | eps, | ||
| real(dp), intent(in) | sfmin, | ||
| real(dp), intent(in) | tol, | ||
| integer(ilp), intent(in) | nsweep, | ||
| real(dp), dimension(lwork), intent(out) | work, | ||
| integer(ilp), intent(in) | lwork, | ||
| integer(ilp), intent(out) | info ) |
◆ la_cgsvj1()
| la_lapack::gsvj1::la_cgsvj1 |
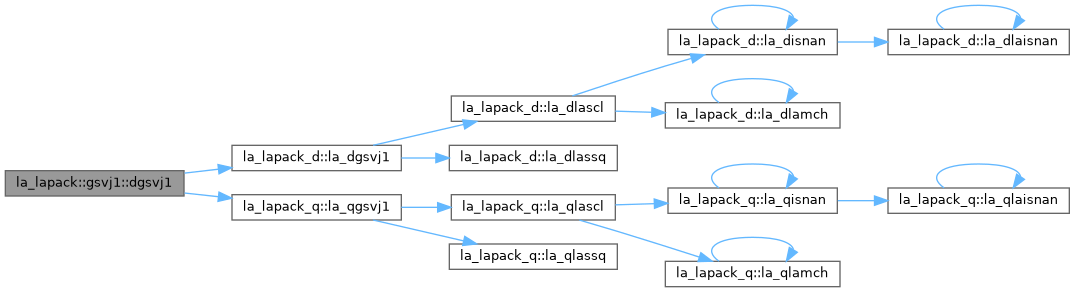
◆ la_dgsvj1()
| la_lapack::gsvj1::la_dgsvj1 |
◆ la_qgsvj1()
| la_lapack::gsvj1::la_qgsvj1 |
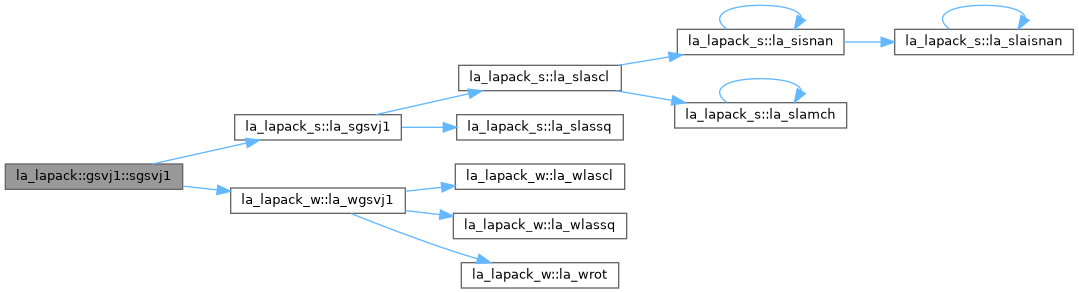
◆ la_sgsvj1()
| la_lapack::gsvj1::la_sgsvj1 |
◆ la_wgsvj1()
| la_lapack::gsvj1::la_wgsvj1 |
◆ la_zgsvj1()
| la_lapack::gsvj1::la_zgsvj1 |
◆ sgsvj1()
| pure subroutine la_lapack::gsvj1::sgsvj1 | ( | character, intent(in) | jobv, |
| integer(ilp), intent(in) | m, | ||
| integer(ilp), intent(in) | n, | ||
| integer(ilp), intent(in) | n1, | ||
| real(sp), dimension(lda,*), intent(inout) | a, | ||
| integer(ilp), intent(in) | lda, | ||
| real(sp), dimension(n), intent(inout) | d, | ||
| real(sp), dimension(n), intent(inout) | sva, | ||
| integer(ilp), intent(in) | mv, | ||
| real(sp), dimension(ldv,*), intent(inout) | v, | ||
| integer(ilp), intent(in) | ldv, | ||
| real(sp), intent(in) | eps, | ||
| real(sp), intent(in) | sfmin, | ||
| real(sp), intent(in) | tol, | ||
| integer(ilp), intent(in) | nsweep, | ||
| real(sp), dimension(lwork), intent(out) | work, | ||
| integer(ilp), intent(in) | lwork, | ||
| integer(ilp), intent(out) | info ) |
◆ zgsvj1()
| pure subroutine la_lapack::gsvj1::zgsvj1 | ( | character, intent(in) | jobv, |
| integer(ilp), intent(in) | m, | ||
| integer(ilp), intent(in) | n, | ||
| integer(ilp), intent(in) | n1, | ||
| complex(dp), dimension(lda,*), intent(inout) | a, | ||
| integer(ilp), intent(in) | lda, | ||
| complex(dp), dimension(n), intent(inout) | d, | ||
| real(dp), dimension(n), intent(inout) | sva, | ||
| integer(ilp), intent(in) | mv, | ||
| complex(dp), dimension(ldv,*), intent(inout) | v, | ||
| integer(ilp), intent(in) | ldv, | ||
| real(dp), intent(in) | eps, | ||
| real(dp), intent(in) | sfmin, | ||
| real(dp), intent(in) | tol, | ||
| integer(ilp), intent(in) | nsweep, | ||
| complex(dp), dimension(lwork), intent(out) | work, | ||
| integer(ilp), intent(in) | lwork, | ||
| integer(ilp), intent(out) | info ) |

The documentation for this interface was generated from the following file: