la_lapack::getrf2 Interface Reference

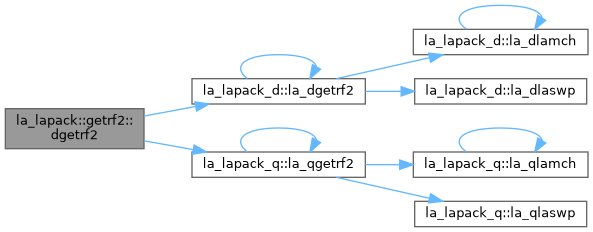
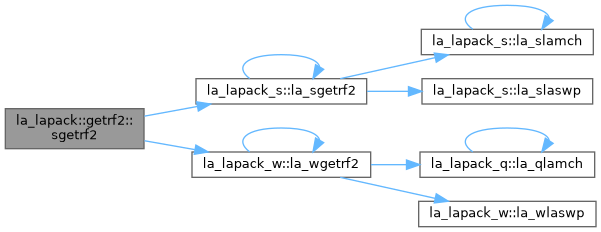
GETRF2: computes an LU factorization of a general M-by-N matrix A using partial pivoting with row interchanges. The factorization has the form A = P * L * U where P is a permutation matrix, L is lower triangular with unit diagonal elements (lower trapezoidal if m > n), and U is upper triangular (upper trapezoidal if m < n). This is the recursive version of the algorithm. It divides the matrix into four submatrices: [ A11 | A12 ] where A11 is n1 by n1 and A22 is n2 by n2 A = [ --—|--— ] with n1 = min(m,n)/2 [ A21 | A22 ] n2 = n-n1 [ A11 ] The subroutine calls itself to factor [ — ], [ A12 ] [ A12 ] do the swaps on [ — ], solve A12, update A22, [ A22 ] then calls itself to factor A22 and do the swaps on A21. More...

Public Member Functions
pure recursive subroutine	cgetrf2 (m, n, a, lda, ipiv, info)
	la_cgetrf2
pure recursive subroutine	dgetrf2 (m, n, a, lda, ipiv, info)
	la_dgetrf2
	la_qgetrf2
pure recursive subroutine	sgetrf2 (m, n, a, lda, ipiv, info)
	la_sgetrf2
	la_wgetrf2
pure recursive subroutine	zgetrf2 (m, n, a, lda, ipiv, info)
	la_zgetrf2

Detailed Description

GETRF2: computes an LU factorization of a general M-by-N matrix A using partial pivoting with row interchanges. The factorization has the form A = P * L * U where P is a permutation matrix, L is lower triangular with unit diagonal elements (lower trapezoidal if m > n), and U is upper triangular (upper trapezoidal if m < n). This is the recursive version of the algorithm. It divides the matrix into four submatrices: [ A11 | A12 ] where A11 is n1 by n1 and A22 is n2 by n2 A = [ --—|--— ] with n1 = min(m,n)/2 [ A21 | A22 ] n2 = n-n1 [ A11 ] The subroutine calls itself to factor [ — ], [ A12 ] [ A12 ] do the swaps on [ — ], solve A12, update A22, [ A22 ] then calls itself to factor A22 and do the swaps on A21.

Member Function/Subroutine Documentation

cgetrf2()

pure recursive subroutine la_lapack::getrf2::cgetrf2	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		complex(sp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(out)	ipiv,
		integer(ilp), intent(out)	info
	)

Here is the call graph for this function:

dgetrf2()

pure recursive subroutine la_lapack::getrf2::dgetrf2	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(out)	ipiv,
		integer(ilp), intent(out)	info
	)

Here is the call graph for this function:

la_cgetrf2()

la_lapack::getrf2::la_cgetrf2

la_dgetrf2()

la_lapack::getrf2::la_dgetrf2

la_qgetrf2()

la_lapack::getrf2::la_qgetrf2

la_sgetrf2()

la_lapack::getrf2::la_sgetrf2

la_wgetrf2()

la_lapack::getrf2::la_wgetrf2

la_zgetrf2()

la_lapack::getrf2::la_zgetrf2

sgetrf2()

pure recursive subroutine la_lapack::getrf2::sgetrf2	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		real(sp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(out)	ipiv,
		integer(ilp), intent(out)	info
	)

Here is the call graph for this function:

zgetrf2()

pure recursive subroutine la_lapack::getrf2::zgetrf2	(	integer(ilp), intent(in)	m,
		integer(ilp), intent(in)	n,
		complex(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		integer(ilp), dimension(*), intent(out)	ipiv,
		integer(ilp), intent(out)	info
	)

Here is the call graph for this function:

---

The documentation for this interface was generated from the following file:

• la_lapack.f90