la_lapack::gges Interface Reference

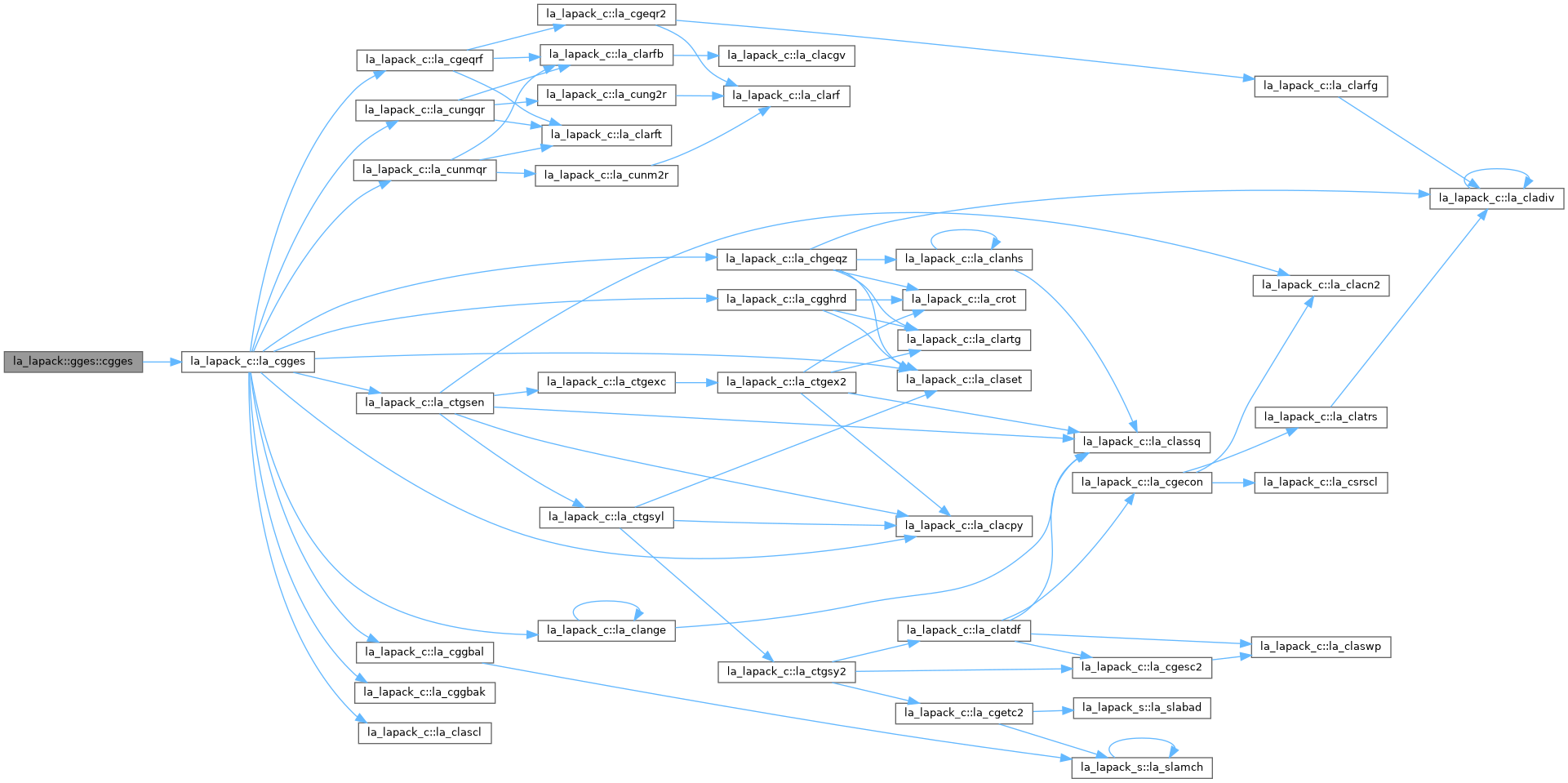
GGES: computes for a pair of N-by-N complex nonsymmetric matrices (A,B), the generalized eigenvalues, the generalized complex Schur form (S, T), and optionally left and/or right Schur vectors (VSL and VSR). This gives the generalized Schur factorization (A,B) = ( (VSL)*S*(VSR)**H, (VSL)*T*(VSR)**H ) where (VSR)**H is the conjugate-transpose of VSR. Optionally, it also orders the eigenvalues so that a selected cluster of eigenvalues appears in the leading diagonal blocks of the upper triangular matrix S and the upper triangular matrix T. The leading columns of VSL and VSR then form an unitary basis for the corresponding left and right eigenspaces (deflating subspaces). (If only the generalized eigenvalues are needed, use the driver CGGEV instead, which is faster.) A generalized eigenvalue for a pair of matrices (A,B) is a scalar w or a ratio alpha/beta = w, such that A - w*B is singular. It is usually represented as the pair (alpha,beta), as there is a reasonable interpretation for beta=0, and even for both being zero. A pair of matrices (S,T) is in generalized complex Schur form if S and T are upper triangular and, in addition, the diagonal elements of T are non-negative real numbers. More...

Public Member Functions
subroutine	cgges (jobvsl, jobvsr, sort, selctg, n, a, lda, b, ldb, sdim, alpha, beta, vsl, ldvsl, vsr, ldvsr, work, lwork, rwork, bwork, info)
	la_cgges
subroutine	dgges (jobvsl, jobvsr, sort, selctg, n, a, lda, b, ldb, sdim, alphar, alphai, beta, vsl, ldvsl, vsr, ldvsr, work, lwork, bwork, info)
	la_dgges
	la_qgges
subroutine	sgges (jobvsl, jobvsr, sort, selctg, n, a, lda, b, ldb, sdim, alphar, alphai, beta, vsl, ldvsl, vsr, ldvsr, work, lwork, bwork, info)
	la_sgges
	la_wgges
subroutine	zgges (jobvsl, jobvsr, sort, selctg, n, a, lda, b, ldb, sdim, alpha, beta, vsl, ldvsl, vsr, ldvsr, work, lwork, rwork, bwork, info)
	la_zgges

Detailed Description

GGES: computes for a pair of N-by-N complex nonsymmetric matrices (A,B), the generalized eigenvalues, the generalized complex Schur form (S, T), and optionally left and/or right Schur vectors (VSL and VSR). This gives the generalized Schur factorization (A,B) = ( (VSL)*S*(VSR)**H, (VSL)*T*(VSR)**H ) where (VSR)**H is the conjugate-transpose of VSR. Optionally, it also orders the eigenvalues so that a selected cluster of eigenvalues appears in the leading diagonal blocks of the upper triangular matrix S and the upper triangular matrix T. The leading columns of VSL and VSR then form an unitary basis for the corresponding left and right eigenspaces (deflating subspaces). (If only the generalized eigenvalues are needed, use the driver CGGEV instead, which is faster.) A generalized eigenvalue for a pair of matrices (A,B) is a scalar w or a ratio alpha/beta = w, such that A - w*B is singular. It is usually represented as the pair (alpha,beta), as there is a reasonable interpretation for beta=0, and even for both being zero. A pair of matrices (S,T) is in generalized complex Schur form if S and T are upper triangular and, in addition, the diagonal elements of T are non-negative real numbers.

Member Function/Subroutine Documentation

cgges()

subroutine la_lapack::gges::cgges	(	character, intent(in)	jobvsl,
		character, intent(in)	jobvsr,
		character, intent(in)	sort,
		procedure(la_selctg_c)	selctg,
		integer(ilp), intent(in)	n,
		complex(sp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		complex(sp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	sdim,
		complex(sp), dimension(*), intent(out)	alpha,
		complex(sp), dimension(*), intent(out)	beta,
		complex(sp), dimension(ldvsl,*), intent(out)	vsl,
		integer(ilp), intent(in)	ldvsl,
		complex(sp), dimension(ldvsr,*), intent(out)	vsr,
		integer(ilp), intent(in)	ldvsr,
		complex(sp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		real(sp), dimension(*), intent(out)	rwork,
		logical(lk), dimension(*), intent(out)	bwork,
		integer(ilp), intent(out)	info
	)

Here is the call graph for this function:

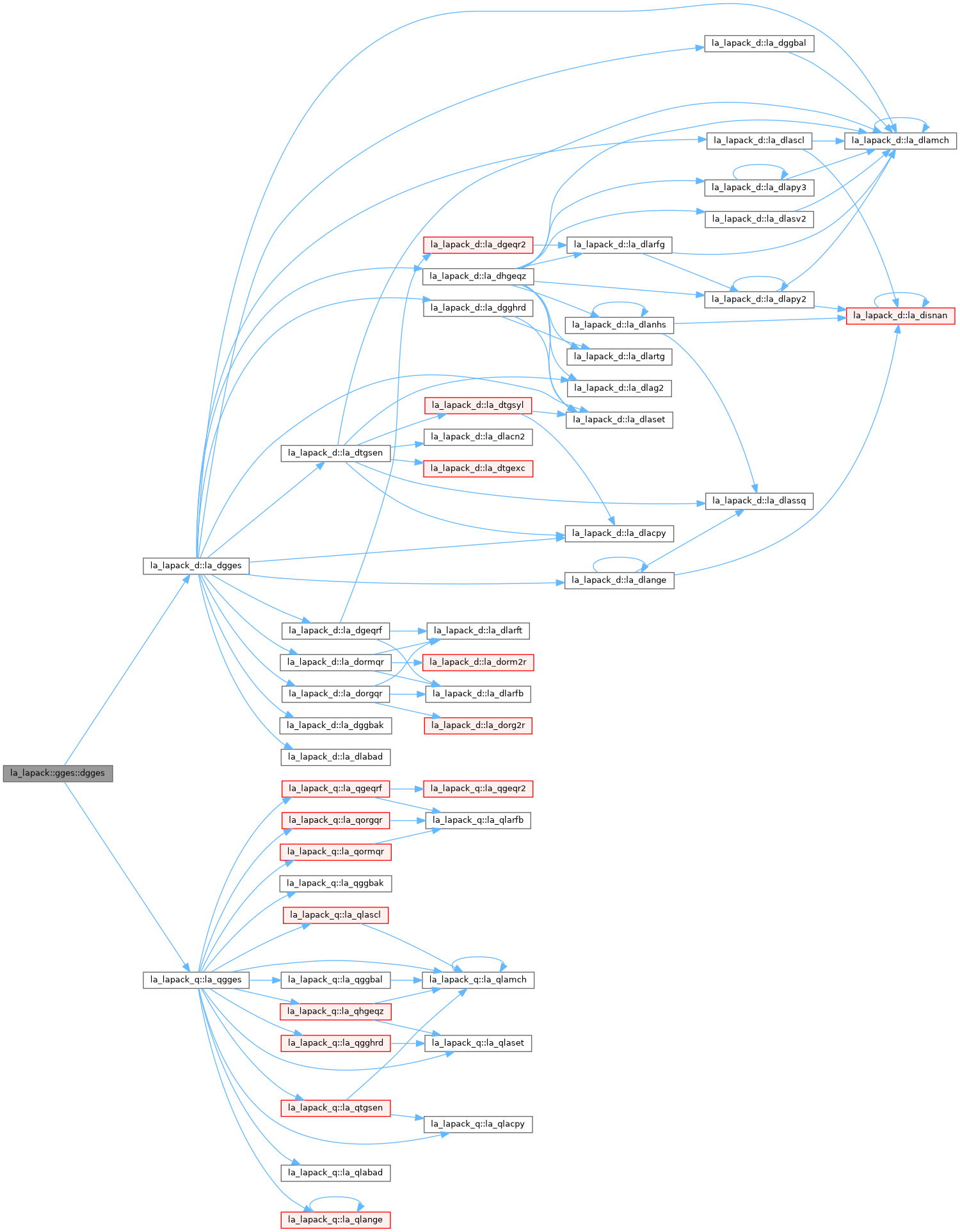
dgges()

subroutine la_lapack::gges::dgges	(	character, intent(in)	jobvsl,
		character, intent(in)	jobvsr,
		character, intent(in)	sort,
		procedure(la_selctg_d)	selctg,
		integer(ilp), intent(in)	n,
		real(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	sdim,
		real(dp), dimension(*), intent(out)	alphar,
		real(dp), dimension(*), intent(out)	alphai,
		real(dp), dimension(*), intent(out)	beta,
		real(dp), dimension(ldvsl,*), intent(out)	vsl,
		integer(ilp), intent(in)	ldvsl,
		real(dp), dimension(ldvsr,*), intent(out)	vsr,
		integer(ilp), intent(in)	ldvsr,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		logical(lk), dimension(*), intent(out)	bwork,
		integer(ilp), intent(out)	info
	)

Here is the call graph for this function:

la_cgges()

la_lapack::gges::la_cgges

la_dgges()

la_lapack::gges::la_dgges

la_qgges()

la_lapack::gges::la_qgges

la_sgges()

la_lapack::gges::la_sgges

la_wgges()

la_lapack::gges::la_wgges

la_zgges()

la_lapack::gges::la_zgges

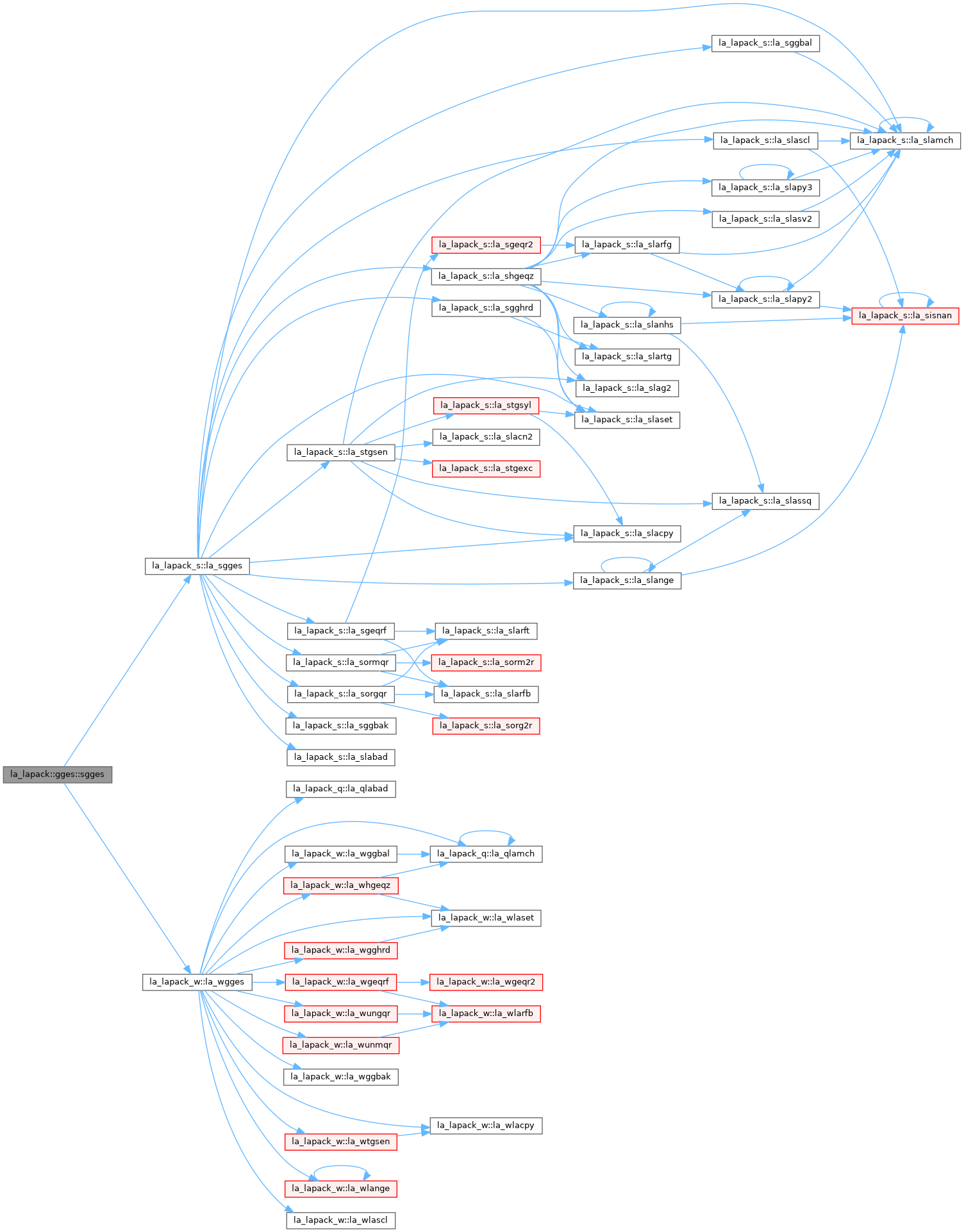
sgges()

subroutine la_lapack::gges::sgges	(	character, intent(in)	jobvsl,
		character, intent(in)	jobvsr,
		character, intent(in)	sort,
		procedure(la_selctg_s)	selctg,
		integer(ilp), intent(in)	n,
		real(sp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		real(sp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	sdim,
		real(sp), dimension(*), intent(out)	alphar,
		real(sp), dimension(*), intent(out)	alphai,
		real(sp), dimension(*), intent(out)	beta,
		real(sp), dimension(ldvsl,*), intent(out)	vsl,
		integer(ilp), intent(in)	ldvsl,
		real(sp), dimension(ldvsr,*), intent(out)	vsr,
		integer(ilp), intent(in)	ldvsr,
		real(sp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		logical(lk), dimension(*), intent(out)	bwork,
		integer(ilp), intent(out)	info
	)

Here is the call graph for this function:

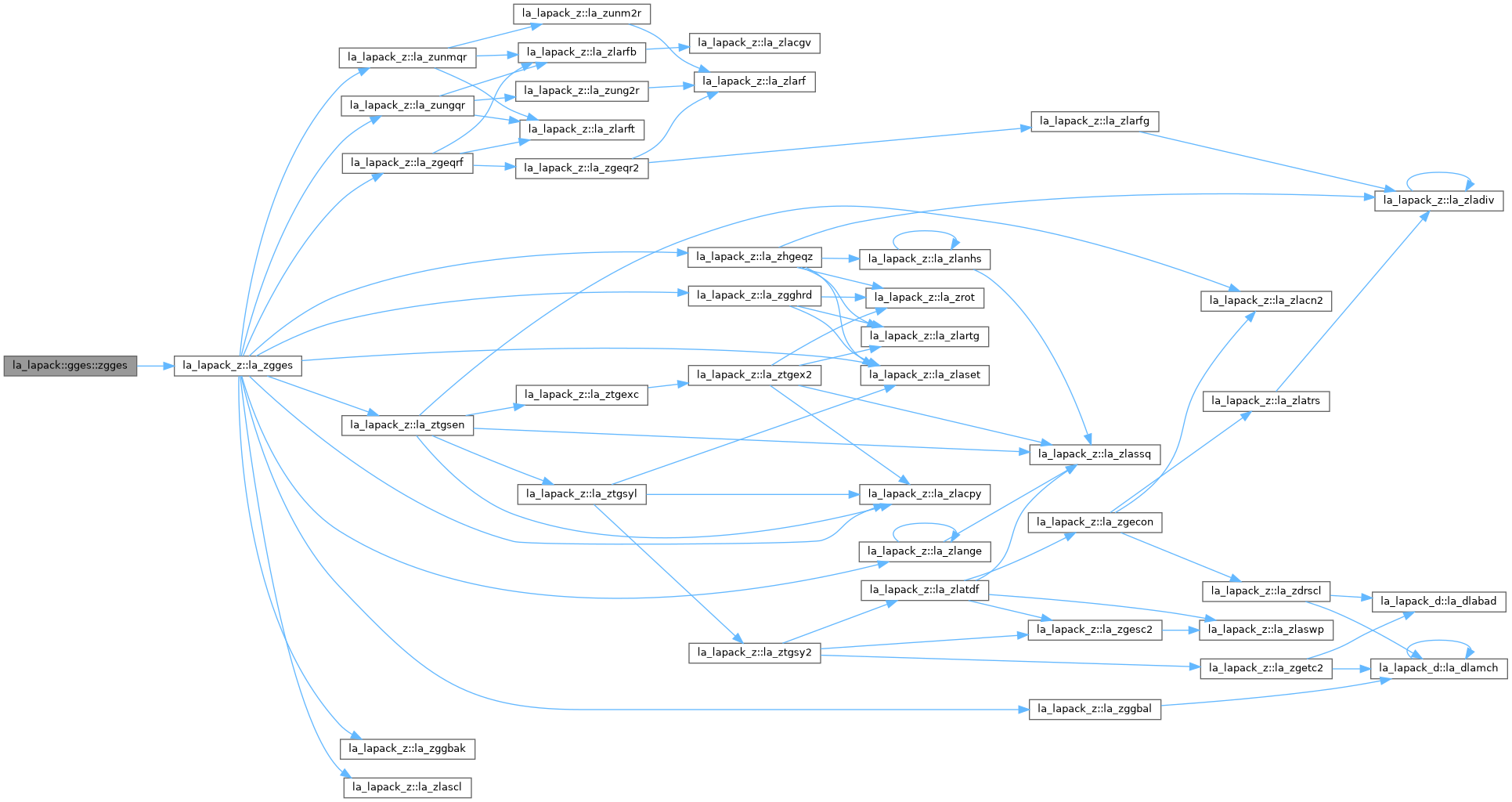
zgges()

subroutine la_lapack::gges::zgges	(	character, intent(in)	jobvsl,
		character, intent(in)	jobvsr,
		character, intent(in)	sort,
		procedure(la_selctg_z)	selctg,
		integer(ilp), intent(in)	n,
		complex(dp), dimension(lda,*), intent(inout)	a,
		integer(ilp), intent(in)	lda,
		complex(dp), dimension(ldb,*), intent(inout)	b,
		integer(ilp), intent(in)	ldb,
		integer(ilp), intent(out)	sdim,
		complex(dp), dimension(*), intent(out)	alpha,
		complex(dp), dimension(*), intent(out)	beta,
		complex(dp), dimension(ldvsl,*), intent(out)	vsl,
		integer(ilp), intent(in)	ldvsl,
		complex(dp), dimension(ldvsr,*), intent(out)	vsr,
		integer(ilp), intent(in)	ldvsr,
		complex(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(in)	lwork,
		real(dp), dimension(*), intent(out)	rwork,
		logical(lk), dimension(*), intent(out)	bwork,
		integer(ilp), intent(out)	info
	)

Here is the call graph for this function:

---

The documentation for this interface was generated from the following file:

• la_lapack.f90