la_lapack::bdsqr Interface Reference

BDSQR: computes the singular values and, optionally, the right and/or left singular vectors from the singular value decomposition (SVD) of a real N-by-N (upper or lower) bidiagonal matrix B using the implicit zero-shift QR algorithm. The SVD of B has the form B = Q * S * P**H where S is the diagonal matrix of singular values, Q is an orthogonal matrix of left singular vectors, and P is an orthogonal matrix of right singular vectors. If left singular vectors are requested, this subroutine actually returns U*Q instead of Q, and, if right singular vectors are requested, this subroutine returns P**H*VT instead of P**H, for given complex input matrices U and VT. When U and VT are the unitary matrices that reduce a general matrix A to bidiagonal form: A = U*B*VT, as computed by CGEBRD, then A = (U*Q) * S * (P**H*VT) is the SVD of A. Optionally, the subroutine may also compute Q**H*C for a given complex input matrix C. See "Computing Small Singular Values of Bidiagonal Matrices With Guaranteed High Relative Accuracy," by J. Demmel and W. Kahan, LAPACK Working Note #3 (or SIAM J. Sci. Statist. Comput. vol. 11, no. 5, pp. 873-912, Sept 1990) and "Accurate singular values and differential qd algorithms," by B. Parlett and V. Fernando, Technical Report CPAM-554, Mathematics Department, University of California at Berkeley, July 1992 for a detailed description of the algorithm. More...

Public Member Functions
pure subroutine	cbdsqr (uplo, n, ncvt, nru, ncc, d, e, vt, ldvt, u, ldu, c, ldc, rwork, info)
	la_cbdsqr
pure subroutine	dbdsqr (uplo, n, ncvt, nru, ncc, d, e, vt, ldvt, u, ldu, c, ldc, work, info)
	la_dbdsqr
	la_qbdsqr
pure subroutine	sbdsqr (uplo, n, ncvt, nru, ncc, d, e, vt, ldvt, u, ldu, c, ldc, work, info)
	la_sbdsqr
	la_wbdsqr
pure subroutine	zbdsqr (uplo, n, ncvt, nru, ncc, d, e, vt, ldvt, u, ldu, c, ldc, rwork, info)
	la_zbdsqr

Detailed Description

BDSQR: computes the singular values and, optionally, the right and/or left singular vectors from the singular value decomposition (SVD) of a real N-by-N (upper or lower) bidiagonal matrix B using the implicit zero-shift QR algorithm. The SVD of B has the form B = Q * S * P**H where S is the diagonal matrix of singular values, Q is an orthogonal matrix of left singular vectors, and P is an orthogonal matrix of right singular vectors. If left singular vectors are requested, this subroutine actually returns U*Q instead of Q, and, if right singular vectors are requested, this subroutine returns P**H*VT instead of P**H, for given complex input matrices U and VT. When U and VT are the unitary matrices that reduce a general matrix A to bidiagonal form: A = U*B*VT, as computed by CGEBRD, then A = (U*Q) * S * (P**H*VT) is the SVD of A. Optionally, the subroutine may also compute Q**H*C for a given complex input matrix C. See "Computing Small Singular Values of Bidiagonal Matrices With Guaranteed High Relative Accuracy," by J. Demmel and W. Kahan, LAPACK Working Note #3 (or SIAM J. Sci. Statist. Comput. vol. 11, no. 5, pp. 873-912, Sept 1990) and "Accurate singular values and differential qd algorithms," by B. Parlett and V. Fernando, Technical Report CPAM-554, Mathematics Department, University of California at Berkeley, July 1992 for a detailed description of the algorithm.

Member Function/Subroutine Documentation

cbdsqr()

pure subroutine la_lapack::bdsqr::cbdsqr	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ncvt,
		integer(ilp), intent(in)	nru,
		integer(ilp), intent(in)	ncc,
		real(sp), dimension(*), intent(inout)	d,
		real(sp), dimension(*), intent(inout)	e,
		complex(sp), dimension(ldvt,*), intent(inout)	vt,
		integer(ilp), intent(in)	ldvt,
		complex(sp), dimension(ldu,*), intent(inout)	u,
		integer(ilp), intent(in)	ldu,
		complex(sp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(sp), dimension(*), intent(out)	rwork,
		integer(ilp), intent(out)	info
	)

Here is the call graph for this function:

dbdsqr()

pure subroutine la_lapack::bdsqr::dbdsqr	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ncvt,
		integer(ilp), intent(in)	nru,
		integer(ilp), intent(in)	ncc,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(inout)	e,
		real(dp), dimension(ldvt,*), intent(inout)	vt,
		integer(ilp), intent(in)	ldvt,
		real(dp), dimension(ldu,*), intent(inout)	u,
		integer(ilp), intent(in)	ldu,
		real(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

Here is the call graph for this function:

la_cbdsqr()

la_lapack::bdsqr::la_cbdsqr

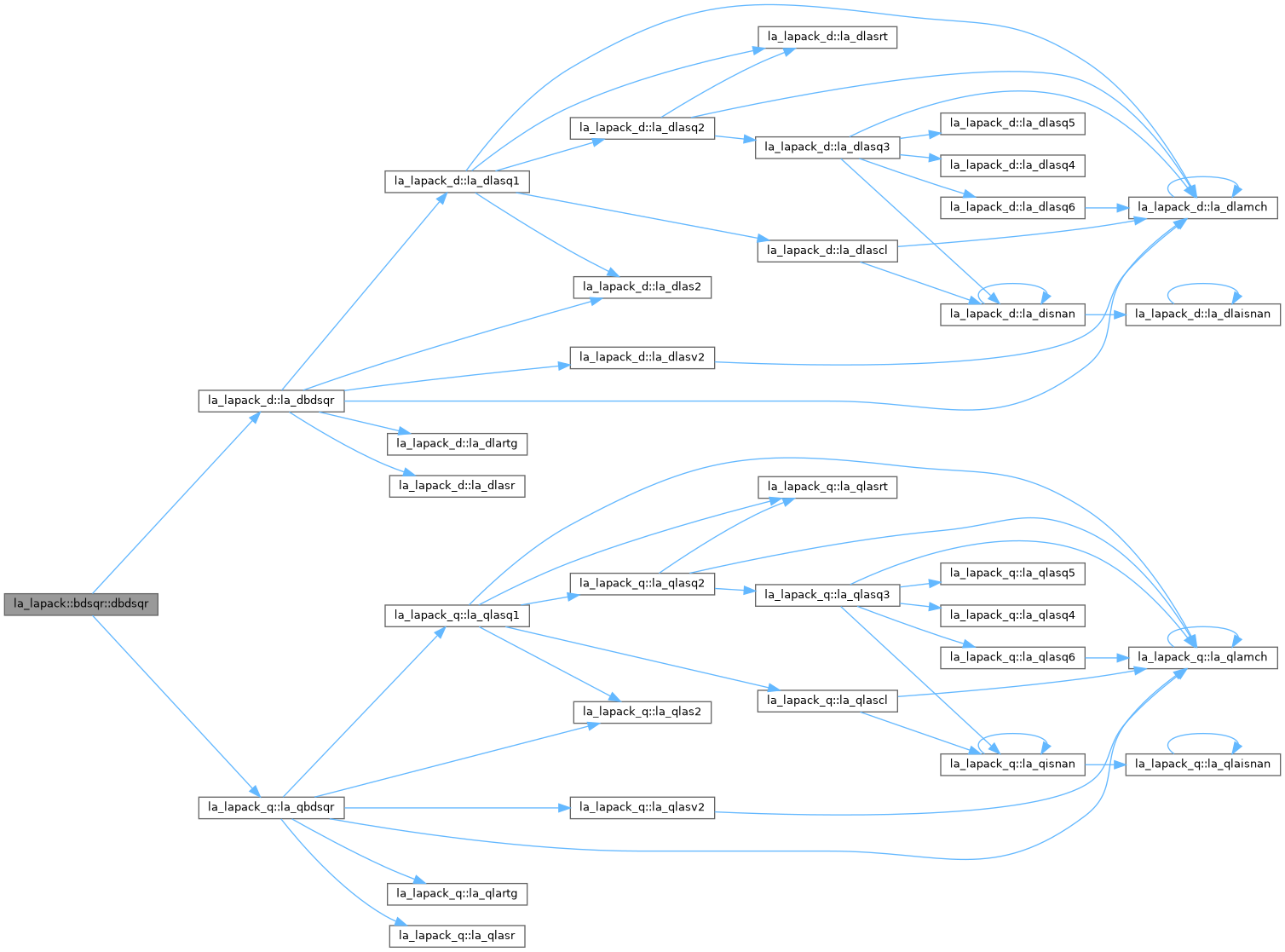
la_dbdsqr()

la_lapack::bdsqr::la_dbdsqr

la_qbdsqr()

la_lapack::bdsqr::la_qbdsqr

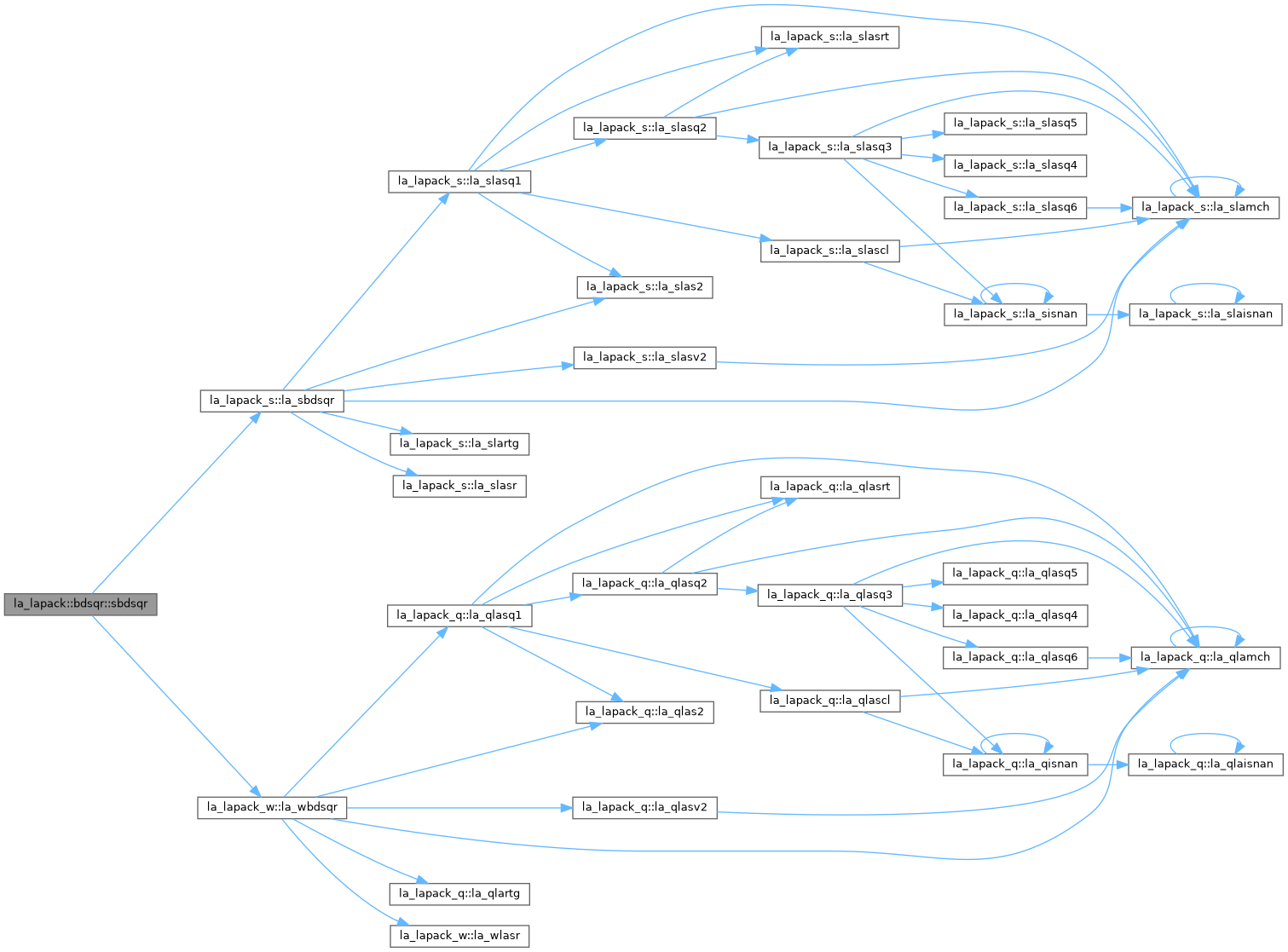
la_sbdsqr()

la_lapack::bdsqr::la_sbdsqr

la_wbdsqr()

la_lapack::bdsqr::la_wbdsqr

la_zbdsqr()

la_lapack::bdsqr::la_zbdsqr

sbdsqr()

pure subroutine la_lapack::bdsqr::sbdsqr	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ncvt,
		integer(ilp), intent(in)	nru,
		integer(ilp), intent(in)	ncc,
		real(sp), dimension(*), intent(inout)	d,
		real(sp), dimension(*), intent(inout)	e,
		real(sp), dimension(ldvt,*), intent(inout)	vt,
		integer(ilp), intent(in)	ldvt,
		real(sp), dimension(ldu,*), intent(inout)	u,
		integer(ilp), intent(in)	ldu,
		real(sp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(sp), dimension(*), intent(out)	work,
		integer(ilp), intent(out)	info
	)

Here is the call graph for this function:

zbdsqr()

pure subroutine la_lapack::bdsqr::zbdsqr	(	character, intent(in)	uplo,
		integer(ilp), intent(in)	n,
		integer(ilp), intent(in)	ncvt,
		integer(ilp), intent(in)	nru,
		integer(ilp), intent(in)	ncc,
		real(dp), dimension(*), intent(inout)	d,
		real(dp), dimension(*), intent(inout)	e,
		complex(dp), dimension(ldvt,*), intent(inout)	vt,
		integer(ilp), intent(in)	ldvt,
		complex(dp), dimension(ldu,*), intent(inout)	u,
		integer(ilp), intent(in)	ldu,
		complex(dp), dimension(ldc,*), intent(inout)	c,
		integer(ilp), intent(in)	ldc,
		real(dp), dimension(*), intent(out)	rwork,
		integer(ilp), intent(out)	info
	)

Here is the call graph for this function:

---

The documentation for this interface was generated from the following file:

• la_lapack.f90